Administrative Structure of the Program
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Elenco Dei Soggetti Collocatori Autorizzati Per La Dis Ri Autorizzati
Elenco dei Soggetti Collocatori autorizzati per la distribuzione in Italia. Distributori Numeri di Sito Internet telefono Allianz 800 22 33 44 www.allianzbank.it/ Alpenbank 0471 301461 www.alpenbank.it/ Arianna SIM 06 4547 4545 www.ariannasim.it Aureo Gestioni 02 43028 600 www.aureo.it/ Banca Alpi Marittime Credito 800154664 www.bancaalpimarittime.it cooperativo Carrù Banca del Piemonte 800 99 80 50 www.bancadelpiemonte.it/ Banca del Valdarno 055 91 371 www.bancavaldarno.it/ Banca della Provincia di Macerata 0733 27 67 11 www.bancaprovinciamacerata.it/ versione1/ Banca di Pistoia Credito Cooperativo 800 92 91 46 www.bancadipistoia.it/ Banca Esperia 02 88219310 www.bancaesperia.it/ Banca Finnat 06 699331 www.finnat.it/ Banca Ifigest 055 24 63 400 https://www.fundstore.it/fs/ fsBancaIfigest.jsp Banca IPIBI Financial Advisory 02 85 906 1 www.bancaipibi.it/ Banca MB (Ex Novagest) 02 321 63 01 www.banca-bmb.it/ Banca Monte Parma 800 85 30 23 www.monteparma.it/ Banca Network 800124500 www.bancanetwork.it/ Banca Passadore & C. 010 53931 www.passbanca.it/ Banca Popolare dell'Alto Adige - 800585600 https://www.bancapopolare.it/it/ Volksbank Banca Popolare di Lajatico 0587 640 896 www.bancalajatico.it/ Banca Popolare di Milano 800100200 www.bpm.it/homepage/default.shtml Banca Popolare di Puglia e Basilicata 800 66 00 01 www.bankpuliabas.it/ Banca Popolare di Roma 800 04 00 41 www.popolareroma.it/ Banca Popolare di Spoleto 800 20 2000 www.bpspoleto.it/ Banca Popolare di Valle d'Itria e 080 480 47 01 www.itriabank.it/ Magna Grecia Banca Profilo 02 58408.1 www.bancaprofilo.it/ Banca Promos 081 050411 www.bancapromos.it/ Banca SAI S.p.A. -

Elenco Collocatori Robeco Capital Growth Fund
ROBECO CAPITAL GROWTH FUNDS Società d’Investimento a Capitale Variabile – SICAV ELENCO DEI SOGGETTI INCARICATI DEL COLLOCAMENTO IN ITALIA Denominazione Soggetto Collocatore Classi Collocate Soggetto incaricato dei pagamenti Alpenbank AG Filiale Bolzano** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Alto Adige Banca S.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Azimut Capital Management SGR S.p.a** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca Aletti S.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca CARIGE S.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca Cesare Ponti S.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca del Monte di Lucca S.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca di Pisa e Fornacette S.C.P.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca Finnat Euramerica S.p.A** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca Generali S.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. Milan Branch Banca Ifigest S.p.A. D, DH, B, BH, E, EH Société Générale Securities Services S.p.A. Banca Leonardo S.p.A.* D, DH, B, BH, E, EH BNP Paribas Securities Services Banca Nazionale del Lavoro S.p.A. D, DH, B, BH, E, EH BNP Paribas Securities Services Banca Popolare del Lazio S.c.p.A.** D, DH, B, BH, E, EH Allfunds Bank S.A. -

Elenco Dei Soggetti Richiedenti Che Operano Con Il Fondo, Con Specifica
Elenco dei soggetti richiedenti che operano con il Fondo – account abilitati all’utilizzo della procedura telematica - Ottobre 2020 (informativa ai sensi del Piano della Trasparenza - parte X delle Disposizioni operative) DENOMINAZIONE SOGGETTO RICHIEDENTE COGNOME NOME E-MAIL TELEFONO AAREAL BANK MAZZA ANTONIO [email protected] 0683004228 AAREAL BANK CIPOLLONE LORELLA [email protected] 0683004305 AGFA FINANCE ITALY SPA CRIPPA ANTONELLA [email protected] 023074648 AGFA FINANCE ITALY SPA BUSTI FILIPPO [email protected] AGRIFIDI ZAPPA GIUSEPPE [email protected] 3371066673 AGRIFIDI EMILIA ROMAGNA TEDESCHI CARLO ALBERTO [email protected] 05211756120 AGRIFIDI MODENA REGGIO FERRARA TINCANI ENNIO EMANUELE [email protected] 059208524 AGRIFIDI UNO EMILIA ROMAGNA EVANGELISTI CARLOTTA [email protected] 0544271787 AGRIFIDI UNO EMILIA ROMAGNA MONTI LUCA [email protected] 0544271787 A-LEASING SPA LOMBARDO CLAUDIO [email protected] 0422409820 ALLIANZ BANK FINANCIAL ADVISORS PISTARINO FRANCA [email protected] 0131035420 ALLIANZ BANK FINANCIAL ADVISORS CORIGLIANO FABIO [email protected] 0272168085 ALLIANZ BANK FINANCIAL ADVISORS CHIARI STEFANO [email protected] 0272168518 ALLIANZ BANK FINANCIAL ADVISORS CANNIZZARO FEDERICO [email protected] 3421650350 ALLIANZ BANK FINANCIAL ADVISORS KOFLER SAMUEL [email protected] 3466001059 ALLIANZ BANK FINANCIAL ADVISORS FERRARI PIERO [email protected] 3477704188 ALLIANZ -

Italy's Less Significant Banks: General Overview and Supervision
Italy’s less significant banks: general overview and supervision On 30 June 2016, Italy’s less significant institutions (LSIs), directly supervised by the Bank of Italy within the framework of Europe’s Single Supervisory Mechanism (SSM), numbered 462, of which 355 were mutual cooperative banks (banche di credito cooperativo or BCCs). LSIs in Italy comprise about 8,700 branches and 74,000 bank employees, while the entire Italian banking system consists of 29,000 branches and 292,000 bank employees; LSIs account for 18 per cent of the banking system’s total assets. The average value of an LSI’s total assets came to just over €1 billion, against an average of €165 billion for significant institutions (SIs). On the same date, the Common Equity Tier 1 (CET1) ratio for LSIs averaged 15.5 per cent, about 4 percentage points more than in 2011 (the CET1 ratio for SIs was 11.7 per cent, representing an increase of 3 percentage points on 2011). Non-performing loans (net of value adjustments) as a share of total loans (NPL ratio) averaged 12.5 per cent (it was 10.5 per cent for SIs). The coverage ratio averaged 43.6 per cent (46.6 per cent for SIs); however, among LSIs there was greater recourse to guarantees. The increase in the coverage ratio recorded on average by LSIs in recent years was starkly higher than that for SIs. In the first half of 2016, the profitability of LSIs, net of extraordinary effects, was in line with that of SIs. The cost- income ratio was substantially similar for LSIs and SIs. -

Italy Strengthens Foreign Direct Investment Regime
CORONAVIRUS: ITALY STRENGTHENS FOREIGN DIRECT INVESTMENT REGIME To tackle the impact of Coronavirus (Covid-19) and its aftermath, the Italian Government has become more protective over Italian strategic sectors and, accordingly, has strengthened the Italian foreign direct investment regime. This move is part of a broader European strategy towards stricter tests and requirements over foreign hostile buyouts. INTRODUCTION On 8 April 2020, the Italian Government ("Government") has adopted the Law Decree n. 23 ("Decree") which broadens its screening powers over foreign direct investments ("FDI"). Firstly, these new provisions extend the scope of the strategic sectors subject to the Government's screening powers. Secondly, even acquisitions of Italian strategic companies from EU subjects must be notified to the Government. Thirdly, the Government enlarges its powers to detect critical acquisitions. It must be pointed out that this new regime is immediately applicable to any acquisitions which are in a pre-closing phase (although the signing has already occurred). In the same vein, the obligations to disclose significant shareholdings into Italian listed companies have been strenghtened. THE EXTENSION OF THE STRATEGIC SECTORS Since 2012 onwards, the Italian FDI regime requires notification to the Government of acquisitions of stakes in companies owning assets in strategic sectors (i.e., defence, public security, energy, transports and communications), if certain thresholds are met. In 2019, the list of sensitive sectors was enlarged including also the broadband electronic communication based on 5G technology (which is subjects to a FDI special regime) and sectors listed in letters a) and b) (as illustrated here below) of the Regulation (EU) 452/20191 ("EU Regulation"). -

Rapporto ANNO 2020 Dati Sui Volumi Di Negoziazione Delle Associate
Rapporto ANNO 2020 Dati sui volumi di negoziazione delle Associate Area Compliance, Markets & Operations 21 GENNAIO 2021 21 gennaio 2021 RAPPORTO ANNO 2020 COMUNICATO STAMPA - RAPPORTO ANNO 2020 Nell’anno del COVID i mercati finanziari hanno dimostrato la propria resilienza Mercato Azionario - La crisi pandemica scatenata dalla diffusione del virus Covid-19 ha inevitabilmente portato Piazza Affari a chiudere l’anno 2020 in territorio negativo con il FTSE Mib che ha perso il 5,40% rispetto alla fine del 2019. Tuttavia, se si considera che alla fine del mese di marzo (durante il lockdown) l’indice perdeva il 27,50% e che alla fine del mese di giugno questa perdita si era ridotta di circa 10 punti percentuali, possiamo concludere che gli investitori, dopo lo shock iniziale, hanno recuperato la fiducia nei mercati finanziari, anche grazie alle misure fiscali e di politica monetaria straordinarie che sono state messe in campo dalle istituzioni europee e dal governo nazionale. Da segnalare, in controtendenza, la performance positiva del FTSE Italia Star che ha guadagnato il 14,10% dalla fine del 2019. Altro aspetto che sarà ricordato dell’anno appena trascorso è sicuramente la crescita del Trading on Line. Dai dati che ASSOSIM ha elaborato per il Sole 24 Ore emerge chiaramente che, rispetto al bimestre gennaio-febbraio 2020, è proseguita nei bimestri successivi la crescita dei controvalori e delle operazioni concluse dagli intermediari specializzati nel TOL. Anche la volatilità mensile, dopo l’impennata d’inizio anno, si è attenuata attestandosi al 14,70% (a dicembre 2019 era al 14,80%). Altra novità rilevante è l’accordo raggiunto tra EU e UK alla fine del periodo transitorio della Brexit. -

Lista Distributori Master.Xlsx
Lista dei Collocatori - Aggiornamento 20 dicembre 2019 Modalità Indirizzo Collocatore In Fuori A Modalità Nome Collocatore Classi Via Cap Città Note sede sede distanza Raccoltà ALLIANZ BANK FINANCIAL ADVISORS SPA A, E, R sì sì sì Piazzale Lodi, 3 20137 Milano PIC, PAC ALPE ADRIA GESTIONI SIM SPA A, E, R sì no no Corso Vittorio Emanuele II, 20 /B 33170 Pordenone PIC Nota 1 ALPENBANK SPA A, E, R sì sì no Piazza del Grano - Kornplatz, 2 39100 Bolzano PIC, PAC Nota 1 ALTO ADIGE BANCA SPA (SÜDTIROL BANK AG) A, E, R sì sì sì Via Esperanto, 1 39100 Bolzano PIC, PAC AQA CAPITAL SRL A, E, R sì sì no Via Cavallotti, 8 20122 Milano PIC Nota 9 AZIMUT CAPITAL MANAGEMENT SPA A, E, R no sì no Via Cusani, 4 20121 Milano PIC, PAC Nota 1 BANCA ALBERTINI SYZ & C A, E, R sì sì no Via Borgonuovo, 14 20121 Milano PIC Nota 1 BANCA ALETTI & C. SPA A, E, R sì sì sì Via Roncaglia, 12 20146 Milano PIC BANCA CARIGE SPA A, E, R sì no no Via Cassa di Risparmio, 15 16123 Genova PIC Nota 1,5 BANCA CESARE PONTI SPA A, E, R sì sì no Piazza del Duomo, 19 20121 Milano PIC Nota 1 BANCA CONSULIA SPA A, E, R sì sì no Corso Monforte, 52 20122 Milano PIC, PAC Nota 9 BANCA CR ASTI SPA E sì no no Piazza Liberta, 23 14100 Asti PIC, PAC Nota 1 BANCA D'ALBA CREDITO COOPERATIVO SC A, E, R sì no no Via Cavour, 4 12051 Alba PIC, PAC Nota 7 BANCA DEL FUCINO SPA A, E, R sì sì sì Via Tomacelli, 107 00186 Roma PIC, PAC BANCA DEL MONTE DI LUCCA SPA A, E, R sì no no Piazza S. -

Nominated Advisers
Nominated Advisers Registro Nomad Registro Nomad Alantra Capital Markets SV S.A. BALDI FINANCE S.p.A. Succursale italiana Via San Damiano, 9 Via Borgonuovo, 16 20122 Milano 20121 Milano www.baldifinance.it www.alantra.com Guido Prati Stefano Bellavita [email protected] [email protected] +39 0522.271220 +39 02.63671601 +39 3356058447 Banca Akros S.p.A. Banca Finnat Euramerica S.p.A. Viale Eginardo, 29 Piazza del Gesù, 49 20149 Milano 00186 Roma www.bancaakros.it www.finnat.it Massimo Turcato Giulio Bastia [email protected] [email protected] +39 02.43444053 +39 06.69933343 Banca IMI S.p.A. Banca Intermobiliare di Piazza Belgioioso, 1 Investimenti e Gestioni S.p.A. 20121 Milano Via Gramsci, 7 www.bancaimi.com 10121 Torino www.bancaintermobiliare.com Massimo Mazzarello [email protected] Umberto Gherardini +39 02.72615380 [email protected] +39 02.99968111 Registro Nomad Banca Mediolanum S.p.A. Banca Profilo S.p.A. Via F. Sforza, 15 Via Cerva, 28 20080 Basiglio (MI) 20122 Milano www.bancamediolanum.it www.bancaprofilo.it Giovanni Reale Marco Baga [email protected] [email protected] +39 02.90496015 +39 02.58408425 BPER Banca S.p.A. CFO SIM S.p.A. Corso Vittorio Emanuele, 31 Via dell’Annunciata, 23/4 41121 Modena 20121 Milano www.bper.it www.cfosim.com Stefano Taioli Luca Di Liddo [email protected] [email protected] +39 059.2022655 +39 02.30343391 EnVent Capital Markets Ltd Epic SIM S.p.A. 25 Savile Row Foro Buonaparte, 12 London W1S2ER 20121 Milano enventcapitalmarkets.co.uk www.epic.it Franco Gaudenti Giuliano V. -

Elenco Banche Convenzionate
OFFERTA XPAY: ELENCO BANCHE 1015 Banco di Sardegna SpA 1030 Banca Monte dei Paschi di Siena SpA 3011 Hypo Alpe Adria Bank 3019 Credito Siciliano 3032 Credito Emiliano SpA 3047 Banca Capasso 3048 Banca del Piemonte SpA 3062 Banca Mediolanum SpA 3083 Ubi Banca Private Investment SpA 3087 Banca Finnat 3084 Banca Cesare Ponti 3104 Deutsche Bank SpA 3111 Unione di Banche Italiane SpA 3124 Banca del Fucino SpA 3127 UGF Banca SpA 3138 Banca Reale 3141 Banca di Treviso 3158 Banca Sistema SpA 3165 IW Bank SpA 3177 Banca Sai SpA 3185 Banca Ifigest 3204 Banca di Legnano 3229 Banca Modenese Spa 3242 Banco di Lucca 3253 Banca Federico Del Vecchio 3259 Nordest Banca 3262 Asset Banca 3265 Banca Promos SpA 3287 Banca Sammarinese d’Investimenti 3301 Carimilo - Cassa dei Risparmi di Milano e della Lombardia 3310 Eticredito Banca Etica Adriatica 3317 Banca della Provincia di Macerata 3323 GBM Banca 3332 Banca Passadore & C. SpA 3336 Credito Bergamasco Offerta XPay: Elenco Banche 1 di 4 3338 Banca Serfina 3353 Banca del Sud 3399 Extra Banca 3403 Imprebanca 3425 Banco di Credito P. Azzoaglio SpA 3426 Credito Peloritano 3440 Banco di Desio e della Brianza 3488 Cassa Lombarda 3493 Cassa Centrale Raiffeisen dell’Alto Adige SpA 3512 Credito Artigiano 3566 Citibank National Associaton 3589 Allianz Bank 3599 Cassa Centrale Banca - Cred. Coop. del Nord Est SpA 5000 Istituto Centrale Banche Popolare Italiane 5018 Banca Popolare Etica 5023 Banca Regionale Sviluppo 5030 Credito Salernitano 5034 Banco Popolare Soc. Coop. 5035 Veneto Banca Holding SpA 5036 Banca Agricola -
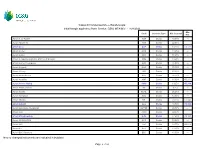
Cassa Di Compensazione E Garanzia Spa Initial Margin Applied to Share Section GEM, MTA/MIV - 16/8/2021 Min
Cassa di Compensazione e Garanzia spa Initial Margin applied to Share Section GEM, MTA/MIV - 16/8/2021 Min. Code Contract Type Mar. Interval Mar. Azioni A. S. ROMA ASR Stocks 49.00% --- Azioni Abitare IN ABT Stocks 22.00% --- Azioni Acea ACE Stocks 13.25% €0.122 Azioni Acotel ACO Stocks 41.25% --- Azioni Aedes AED Stocks 51.25% --- Azioni Aeroporto Guglielmo Marconi di Bologna ADB Stocks 18.25% --- Azioni Alerion Cleanpower ARN Stocks 25.00% --- Azioni Algowatt ALW Stocks 30.75% --- Azioni Alkemy ALK Stocks 25.00% --- Azioni Ambienthesis ATH Stocks 26.75% --- Azioni Amplifon AMP Stocks 13.00% €0.260 Azioni Anima Holding ANIM Stocks 19.25% €0.038 Azioni Antares Vision AV Stocks 9.25% --- Azioni Aquafil ECNL Stocks 26.25% --- Azioni Ascopiave ASC Stocks 13.00% --- Azioni Atlantia ATL Stocks 23.75% €0.146 Azioni Autogrill AGL Stocks 33.50% €0.082 Azioni Autostrade Meridionali AUTME Stocks 26.50% --- Azioni Avio AVIO Stocks 22.50% --- Azioni Azimut Holding AZM Stocks 17.50% €0.182 Azioni ACSM AGAM ACS Stocks 19.00% --- Azioni A2A A2A Stocks 14.75% €0.012 Azioni B.F. BFG Stocks 13.50% --- Azioni B&C Speakers BEC Stocks 13.00% --- New or changed instruments are indicated in boldface Page 1 of 16 Cassa di Compensazione e Garanzia spa Initial Margin applied to Share Section GEM, MTA/MIV - 16/8/2021 Min. Code Contract Type Mar. Interval Mar. Azioni Banca Carige CRG Stocks 97.50% --- Azioni Banca Carige Rnc CRGR Stocks 96.50% --- Azioni Banca Farmafactoring BFF Stocks 17.25% --- Azioni Banca Finnat BFE Stocks 16.75% --- Azioni Banca Generali BGN -

List of Market Makers and Authorised Primary Dealers Who Are Using the Exemption Under the Regulation on Short Selling and Credit Default Swaps
Last update 11 August 2021 List of market makers and authorised primary dealers who are using the exemption under the Regulation on short selling and credit default swaps According to Article 17(13) of Regulation (EU) No 236/2012 of the European Parliament and of the Council of 14 March 2012 on short selling and certain aspects of credit default swaps (the SSR), ESMA shall publish and keep up to date on its website a list of market makers and authorised primary dealers who are using the exemption under the Short Selling Regulation (SSR). The data provided in this list have been compiled from notifications of Member States’ competent authorities to ESMA under Article 17(12) of the SSR. Among the EEA countries, the SSR is applicable in Norway as of 1 January 2017. It will be applicable in the other EEA countries (Iceland and Liechtenstein) upon implementation of the Regulation under the EEA agreement. Austria Italy Belgium Latvia Bulgaria Lithuania Croatia Luxembourg Cyprus Malta Czech Republic The Netherlands Denmark Norway Estonia Poland Finland Portugal France Romania Germany Slovakia Greece Slovenia Hungary Spain Ireland Sweden Last update 11 August 2021 Austria Market makers Name of the notifying Name of the informing CA: ID code* (e.g. BIC): person: FMA ERSTE GROUP BANK AG GIBAATWW FMA OBERBANK AG OBKLAT2L FMA RAIFFEISEN CENTROBANK AG CENBATWW Authorised primary dealers Name of the informing CA: Name of the notifying person: ID code* (e.g. BIC): FMA BARCLAYS BANK PLC BARCGB22 BAWAG P.S.K. BANK FÜR ARBEIT UND WIRTSCHAFT FMA BAWAATWW UND ÖSTERREICHISCHE POSTSPARKASSE AG FMA BNP PARIBAS S.A. -
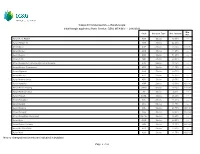
Cassa Di Compensazione E Garanzia Spa Initial Margin Applied to Share Section GEM, MTA/MIV - 28/6/2021 Min
Cassa di Compensazione e Garanzia spa Initial Margin applied to Share Section GEM, MTA/MIV - 28/6/2021 Min. Code Contract Type Mar. Interval Mar. Azioni A. S. ROMA ASR Stocks 49.00% --- Azioni Abitare IN ABT Stocks 22.00% --- Azioni Acea ACE Stocks 13.25% €0.106 Azioni Acotel ACO Stocks 41.25% --- Azioni Aedes AED Stocks 51.25% --- Azioni Aeffe AEF Stocks 20.50% --- Azioni Aeroporto Guglielmo Marconi di Bologna ADB Stocks 18.25% --- Azioni Alerion Cleanpower ARN Stocks 41.75% --- Azioni Algowatt ALW Stocks 30.75% --- Azioni Alkemy ALK Stocks 25.00% --- Azioni Ambienthesis ATH Stocks 29.75% --- Azioni Amplifon AMP Stocks 13.00% €0.186 Azioni Anima Holding ANIM Stocks 19.25% €0.038 Azioni Antares Vision AV Stocks 9.25% --- Azioni Aquafil ECNL Stocks 26.25% --- Azioni Ascopiave ASC Stocks 13.00% --- Azioni Astaldi AST Stocks 41.75% --- Azioni Atlantia ATL Stocks 23.75% €0.146 Azioni Autogrill AGL Stocks 33.50% €0.094 Azioni Autostrade Meridionali AUTME Stocks 26.50% --- Azioni Avio AVIO Stocks 22.50% --- Azioni Azimut Holding AZM Stocks 17.50% €0.164 Azioni ACSM AGAM ACS Stocks 19.00% --- Azioni A2A A2A Stocks 14.75% €0.012 New or changed instruments are indicated in boldface Page 1 of 16 Cassa di Compensazione e Garanzia spa Initial Margin applied to Share Section GEM, MTA/MIV - 28/6/2021 Min. Code Contract Type Mar. Interval Mar. Azioni B.F. BFG Stocks 13.50% --- Azioni B&C Speakers BEC Stocks 13.00% --- Azioni Banca Carige CRG Stocks 97.50% --- Azioni Banca Carige Rnc CRGR Stocks 96.50% --- Azioni Banca Farmafactoring BFF Stocks 17.25%