DOCSLIB.ORG

Cranfield University Colin Morison the Resistance Of

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cranfield University Colin Morison the Resistance Of CRANFIELD UNIVERSITY COLIN MORISON THE RESISTANCE OF LAMINATED GLASS TO BLAST PRESSURE LOADING AND THE COEFFICIENTS FOR SINGLE DEGREE OF FREEDOM ANALYSIS OF LAMINATED GLASS. DEFENCE COLLEGE OF MANAGEMENT AND TECHNOLOGY PhD THESIS CRANFIELD UNIVERSITY DEFENCE COLLEGE OF MANAGEMENT AND TECHNOLOGY ENGINEERING SYSTEMS DEPARTMENT PhD THESIS Academic Year 2006-2007 Colin Morison The resistance of laminated glass to blast pressure loading and the coefficients for single degree of freedom analysis of laminated glass. Supervisor: Dr P D Smith May 2007 © Cranfield University 2007. All rights reserved. No part of this publication may be reproduced without the written permission of the copyright owner Abstract For terrorist explosions or accidental explosions in urban areas, the greatest threat of death and serious injury comes from the effects of glass fragments. Laminated glazing has been proven by trials and experience of actual events to eliminate the risk of significant fragment injury to people behind the glazing, and also to provide substantial protection from blast injury effects, provided that after cracking it remains as a continuous membrane substantially attached to the supporting frame. However, design of laminated glazing is currently based on extrapolation from testing, with limited understanding of the material behaviour that underlies the behaviour under blast loading. This thesis presents an investigation into the application of a simplified method of dynamic analysis for laminated glass, the development of parameters derived from the properties of the materials in laminated glass and the behaviour of laminated glass systems that can be applied to the design of laminated glazing to resist blast loading. The development of the single degree of freedom method for analysis of dynamic response is reviewed from its inception use for analysis of glazing, through its adaptation for reinforced concrete analysis, to its modern use for analysis of glazing. Although the principles of the method are widely applicable, some procedures established for elastic-plastic reinforced concrete analysis in the 1950s are not appropriate for glazing, and should be treated with care. Coefficients for analysis of reinforced concrete date from approximate analyses in the 1950s and 60s and are not accurate. New calculations using advanced yield line models and finite element analysis have been used to provide alternative coefficients for rectangular panels supported on four edges. The elastic analyses for reinforced concrete are linear because they are based on small-deflection theory. Deflections of most uncracked glass panes exceed the limits of this theory. The development of practical non-linear large-deflection analyses in the 1980s was dependent on numerical methods and computer analysis, but they have previously only been applied to resistance and cracking. New non-linear finite element analyses refine the existing resistance data, and data from the same calculations has been used to derive large deflection single degree of freedom parameters for dynamic analysis and to assess the reaction distribution. The cracking of glass arises from small flaws in its surface, and can be very variable in its onset. In addition, the strength is sensitive to the loading rate. Statistical approaches have been based on quasi-static tests, either assuming a normal distribution, or using a more complex Weibull distribution. However, statistical refinement gains little, as strengths then need to be increased for the faster loading under blast. Back-analysis of extensive blast tests had been used to establish deterministic lower bound design cracking strengths for different types of glass. These have been applied in this thesis for design, and back-analysis of blast trials indicates that the design cracking strengths are lower bound. Formulae for a monolithic pane with equivalent behaviour to a laminated glass pane are proposed that would allow the large deflection analysis to be applied to laminated i glass up to cracking of the final ply. The results of some blast trials of uncracked laminated glass are reported which are consistent with an equivalent monolithic analysis. They indicate that laminated glass under blast can be taken as fully composite to temperatures approaching 20ºC, but that it is not fully composite at 29ºC or above. Unfortunately, there is currently no data to indicate the performance in the critical temperature range between. After laminated glass cracks, the resistance is provided by an interlayer of the viscoelastic polymer, Polyvinyl Butyral. Though research is ongoing, non-linear viscoelastic material models for finite element analyses have not yet been developed to the point that they can reproduce the full range of behaviour observed in the tensile tests over the range of temperatures and elongation rates which are reported in the thesis. Instead, the results of the tensile tests are fitted to a simple bilinear material model by back-analysis of the tensile tests to give three stiffness and strength parameters that vary with temperature and strain rate. Non-linear finite element analyses of PVB membranes corresponding to two series of laminated glass blast trials are used to produce single degree of freedom parameters for membrane response. The blast trials are reported, and back-analysis of the deflection histories is used to estimate the ratio of the PVB material strain rates and the observed laminated glass strain rates for the best-fit calculated response. This ratio, found to have a mean value of 3.8, is expected to reflect the stiffening of PVB by attached glass fragments, together with other factors. However, the scatter in the data is large, so the reliability of this figure should be viewed with this in mind. Laminated glass providing blast protection is normally maintained close to room temperature, so a design based on a room temperature of 23ºC is proposed, using single degree of freedom data that is a composite of the uncracked data up to cracking and the membrane data after that point. For normal laminated glazing where the observed strain rate is expected to be about 10 /s, design membrane properties based on a PVB strain rate of 40 /s are proposed, but this may need to be modified for other cases. Typical design cases for marginal behaviour are analysed on this basis, and also for material properties at temperatures 6ºC higher and lower than 23ºC, to assess the sensitivity of the design to likely temperature variations. These indicate that a margin of 16-21% may be needed on deflection limits to allow for temperature increases, but that the calculated deflections would still be below the maximum deflections observed in the trials without PVB failure. The analyses indicate that the peak reactions are unlikely to be sensitive to temperature. However, they indicate that a margin of safety of 2.4 will need to be incorporated in the design anchorage strength to resist in-plane tension in the PVB membrane at reduced temperature. The thesis develops an improved design method under blast loading for laminated glass and double glazing incorporating laminated glass, although some of the values used in the method should be considered tentative. The thesis also indicates a level of anchorage strength sensitivity to temperature reductions that needs to be taken into account in practical glazing designs. ii Acknowledgements My hearfelt thanks go to Dr Peter Smith, my academic supervisor for this research and the writing of this thesis, for his unstinting support throughout the six year gestation period, and for his assistance in so many different ways – Thank you Peter. My sincere thanks also go to Dr Michael Iremonger and Dr Tim Rose, the other members of my thesis committee for their regular help and guidance. I cannot acknowledge too highly the contribution to this research made by Permasteelisa, and particularly by Marc Zobec, their chief engineer and research and development director, who has funded commercial research into laminated glass curtain-walling, involved me in that research and given me permission to use the results of that research in this thesis. This thesis would be a poorer (and thinner) document without my access to that research. Others at Permasteelisa who have actively helped with the research include Luca de Bertoli and Alberto Franceschet. I would like to acknowledge the role of the Home Office Scientific Development Branch and its predecessors in forwarding the research into blast resistance of glazing in the UK, and disseminating their results to those active in the counter-terrorist design field. They, more than anyone, have provided the state of the art on which I have been trying to improve by this research. I would particularly wish to thank Nick Johnson for his guidance and advice over the years, and Kevin Claber and Bob Sheldon for providing data from their tests. I would like to acknowledge my managers at TPS over this period, Steve Harvey and Chris Bowes, who allowed me to use valuable software and the extensive library of explosives-related documents for my own purposes, and my colleagues in the Explosion Effects division, Darius Aibara, David Brettell, Malcolm Connell, Carson Holmes, Ken Holt and Paul Jackson for their tolerance of ‘brain picking’, book borrowing and ideas being bounced off them. Particular individuals that I would like to thank for material assistance or information include: Kevin Webster of Romag Ltd, who donated the PVB tested at Shrivenham. Malcolm Connell who introduced me to the wealth of World War II research on the effects of blast on glazing. Dr Tim Rose, who provided one paper that opened up to me the field of viscoelasticity in PVB. Mike Crossley, who provided the key words ‘Griffith flaws’ that gave me the connection between glazing and fracture mechanics, and who provided a number of useful references from his library on glazing. iii John Williams of HSBC, who provided additional information and photographs of the HSBC building in Istanbul. I would like to thank the scientists, engineers, technicians and support staff that run the test facilities and specialist test equipment, and without whom there would be no test data.
Load more

Recommended publications
  • Perfectly Aligned for Glass Silent Chain Technology for the Glass Industry 2 Inverted Tooth Chains for the Glass Industry I Expertise
    Tooth Chain Perfectly Aligned for Glass Silent Chain Technology for the glass industry 2 Inverted tooth chains for the glass industry I Expertise Safe, robust, and efficient. The glass industry is demanding. Drive and transport solutions not only need to reliably master operating processes, they also need to be highly resistant to harsh conditions and incredibly efficient. Inverted tooth chains cover all these requirements. They offer precise running characteristics, guarantee a long service life, and enable layouts optimized for specific applications with the utmost ef- ficiency. And they have no qualms when it comes to high temperatures. Expertise I Inverted tooth chains for the glass industry 3 Experience for the glass industry Automation solutions with inverted tooth chains from Renold ensure cost-effective production Tailor-made for your application: drive and transport Content solutions with inverted tooth chains The diverse tasks and working conditions in the glass industry require solutions that are just as varied. Based on a compre- 04 Industries – markets – requirements hensive product program and specific configurations, we have 06 Development of glass production geared our spectrum of services toward our users to consistently ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– offer solutions that are specifically tailored to their applications. 08 Industrial production process With unparalleled product quality and expert service. Auto- ––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– mation solutions with inverted tooth chains from Renold help 10 Tasks of inverted tooth chains you to significantly increase the service life of your systems, 12 Drive and transport solutions minimize downtimes, and ensure cost-effective production in 12 Hollow glass industry the long term. Our inverted tooth chains master these goals – 14 Sheet glass industry every day, around the world.
    [Show full text]
  • Standard Documentation Series
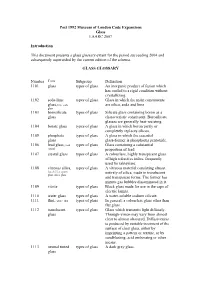
    Post 1992 Museum of London Code Expansions Glass LAARC 2007 Introduction This document presents a glass glossary extant for the period succeeding 2004 and subsequently superseded by the current edition of the schema. GLASS GLOSSARY Number Term Subgroup Definition 1101 glass types of glass An inorganic product of fusion which has cooled to a rigid condition without crystallizing. 1102 soda-lime types of glass Glass in which the main constituents glass, lime-soda are silica, soda and lime. glass 1103 borosilicate types of glass Silicate glass containing boron as a glass characteristic constituent. Borosilicate glasses are generally heat-resisting. 1104 borate glass types of glass A glass in which boron partly or completely replaces silicon. 1105 phosphate types of glass A glass in which the essential glass glass-former is phosphorus pentoxide. 1106 lead glass, lead types of glass Glass containing a substantial crystal proportion of lead. 1107 crystal glass types of glass A colourless, highly transparent glass of high refractive index, frequently used for tableware. 1108 vitreous silica, types of glass A vitreous material consisting almost fused silica, quartz entirely of silica, made in translucent glass, silica glass and transparent forms. The former has minute gas bubbles disseminated in it. 1109 vitrite types of glass Black glass made for use in the caps of electric lamps. 1110 water glass types of glass A water-soluble sodium silicate. 1111 flint, white flint types of glass In general, a colourless glass other than flat glass. 1112 translucent types of glass Glass which transmits light diffusely. glass Through-vision may vary from almost clear to almost obscured.
    [Show full text]
  • Long-Distance Migrant Workers in Nineteenth-Century Britain: a Case Study of St
    LONG-DISTANCE MIGRANT WORKERS IN NINETEENTH-CENTURY BRITAIN: A CASE STUDY OF ST. HEEENS' GEASSMAKERS J.T.Jackson, B.A., Ph.D. AVENSTEIN, drawing mainly from the published R census of 1881, defined long-journey migrants in the British Isles as people who had migrated beyond both their county of birth and the bordering counties' and suggested that they probably accounted for less than 25 per cent of all migrants in the British Isles. 2 At the same time Ravenstein indicated that most long-journey migrants would 'generally go by preference to one of the great cities of commerce and industry'. 3 Such generalisations still remain to be fully tested by later authors. Taken together, they suggest that most county towns and probably all the smaller market towns would have less than 25 per cent of total population coming from beyond their immediate county and surrounding counties' borders, while all major cities would receive more than 25 per cent of their migrant population from non- adjacent counties. This is borne out for 1851 by census data for that year (see Table 1, column 4). Of the mainland urban centres, only Cambridge, Chester and Gloucester of the county towns exceed the 25 per cent figure for long-journey migrants and only Sheffield of the major cities comes close to falling below it. Even if Irish-born are excluded, seven of the ten major cities still had 25 per cent or more of their migrant population classified as long-journey migrants (Figure 1, column 5). 4 Such resultsare not too surprising and perhaps more interesting is the more variable concentration of long- journey migrants in the intermediate-sized industrial towns.
    [Show full text]
  • Architectural Glass
    Architectural glass From Wikipedia, the free encyclopedia Architectural glass has been used in buildings since the 11th century. Glass is typically used in buildings as a transparent glazing material for windows in the building envelope. Glass is also used in glazed internal partitions and as an architectural feature. Glass in buildings is often of a safety type, including toughened and laminated glasses. Crown glass: The earliest style of glass window the concentric arcs that distort some of these panes indicate they are crown glass, possibly of the 16th century. The earliest method of glass window manufacture was the crown glass method. Hot blown glass was cut open opposite the pipe, then rapidly spun on a table before it could cool. Centrifugal force forced the hot globe of glass into a round, flat sheet. The sheet would then be broken off the pipe and trimmed to form a rectangular window to fit into a frame. At the center of a piece of crown glass, a thick remnant of the original blown bottle neck would remain, hence the name "bullseye." Optical distortions produced by the bullseye could be reduced by grinding the glass. The development of diamond pane windows was in part due to the fact that three regular diaper shaped panes could be conveniently cut from a piece of Crown glass, with minimum waste and with minimum distortion. This method for manufacturing flat glass panels was very expensive and could not be used to make large panes. It was replaced in the 19th century by the cylinder, sheet and rolled plate processes, but it is still used in traditional construction and restoration.
    [Show full text]
  • 19 July 1983, No 3
    THE AUSTRALIANA SOCIETY —sf^p ~ ; Mp a» ' I', 1 \ {1 •• \ § \ i . «__. * * ' " • •'*k. ; ^RIAMAMBMELeotl! 4 '•' \ W I * - ^^H^r^^a^v^^B « / -^ It A ©SMTE^AF - , ^/flj $,'"% * yrjM k "V* • "" _^, ^gf jg| , ^|l g 33^ ^ - " f J*! *-^ J ^^^^^^ ^ li.-u.,^^ ZZa^ ^ THE AUSTRALIANA SOCIETY NEWSLETTER ISSN 0156.8019 Published by: The Australiana Society Box A 378 1983, No.3 July, 1983 Sydney South NSW 2000 CONTENTS REGULAR FEATURES Society Information p. h Editorial p. h Letters to the Editor p. 6 Australiana News p. 7 List of I 1lustrations p.11 From Here and There p. 12 Book Reviews p.31 ARTICLES Glass In Australia, 1788-1939, by Annette Keenan p.14 Exhibition Review: Carnival Glass at Hunters Hill, by Annette Keenan p.29 Advertising Information p. B Membership Form P.33 Guidelines for Contributors p.34 Editor: John Wade All editorial correspondence should be addressed to John Wade, c/- Museum of Applied Arts and Sciences, 659 Harris Street, Ultimo, NSW, 2007. Enquiries regarding membership, subscriptions and back issues should be addressed to the Secretary, The Australiana Society, Box A 378, Sydney South, NSW, 2000. Copyright © 1983 The Australiana Society. production: P Renshaw (02) 816 1846 Society Information The annual auction will follow the Annual General Meeting to be held at 7.30 pm on Thursday, ^tth August 1983 at James R Lawson' s auction rooms, Cumberland Street, Sydney. As with previous auctions, ten per cent of the selling price is deducted as the Society's tithe. Bring along the things you want to sell and money for the things you'll want to buy.
    [Show full text]
  • 1900. Catherine Ross a Thesis S
    NE', Vý TYNI E ýy No. V4 LOCATION THE DEVELOPMENTOF THE GLASS INDUSTRY ON THE RIVERS 1900. TYNE AND WEAR , 1700 - Catherine Ross A thesis submitted for the degree of Doctor of Philosophy from the University of Newcastle upon Tynes 1982. - 449a - rP '71'Y'kI i J;, 1 -I N 8 2.'R -' --'943 LOCATION PART 11 1850 - 1900. Text cut off in original - 450 - CHAPTER SIX: THE CHANGING FACE OF THE NORTH-EAST GLASS INDUSTRY, 1850 - 1900 To Collingwood Bruce writing in 1863, "probably no section of the manufactures of the Tyne and Wear has experienced more marked changes during 1 the last twenty five years than that of glass. ' Even looking at the industry from a distance the changes in the appearance and character of the north-east glass industry during the middle of the century are still striking. Looking at the glass industry during the last fifty years of the nineteenth century it is difficult to find much in common with the industry that had flourished in the region for the previous hundred and fifty years. By the 1870s local glass firms were operating on a new scale, the centre of the industry within the region had made a significant shift, certain branches of the industry had disappeared completely and new branches had become est- ablished. These changes were startling but they were to be followed by even more dramatic and disturbing changes during the last thirty years of the century. Again, the individual branches of the industry during this period will be looked at in detail in the following three chapters but it is worth beginning by looking at the north-east glass industry as a whole during the last half of the nineteenth century and the general factors influencing its development, or more accurately its decline, during this period.
    [Show full text]
  • Through the Looking Glass: Transparency in Modern
    TITLE: THROUGH THE LOOKING GLASS: TRANSPARENCY IN MODERN ARCHITECTURE CONTENT OBJECTIVES UBJECTS OPICS MERICAN ISTORY RT RCHITECTURE S /T : A H , A , A , SOCIAL STUDIES Explore case studies of GRADE LEVEL: K-12 architectural glass and establish UTHOR EVIN OFMANN D a chronology A : K H , M.S.E . BACKGROUND Identify, define, and apply Mesopotamian civilizations first began making small glass essential vocabulary and terminology associated with objects around 2500 BCE. Used as an architectural material significant periods of first by the Romans, the production of glass declined in the development fifth century only to return as a decorative artform (stained glass) in Renaissance ecclesiastical architecture. Towards the end of the 19th century, rolled plate glass replaced Examine primary documents and connect the development glassblowing, and business owners began using larger, of architectural glass to broader clearer pieces of glass for their storefronts to sell goods. themes of technology, The development of steel framing, in addition to enabling economics, and culture the construction of taller buildings, forever freed the wall from its load-bearing conformity with structure. Soon, Prompt students to consider architects began specifying glass in both commercial and the future of architectural domestic settings in ways that promoted the use of natural glass as a key area of light, offered uninterrupted views, and contributed to a innovation regarding energy usage in contemporary building’s legibility (i.e., form follows function). Analyzing architecture the use of glass in modern architecture provides students an opportunity to examine the intersection among modern technology, economics, and culture. 1 All rights reserved © 2019 Society of Architectural Historians http://sah-archipedia.org This project is supported in part by an award from the National Endowment for the Humanities LESSON OVERVIEW This scaffolded lesson plan encourages students to connect the use of an architectural material—glass—with broader ESSENTIAL themes of history, technology, and culture.
    [Show full text]
  • The Conservation of Applied Surface Decoration of Historic Stained Glass Windows
    What’s On the Surface Does Matter: The Conservation of Applied Surface Decoration of Historic Stained Glass Windows Alyssa Grieco Submitted in partial fulfillment of the requirement for the degree Master of Science in Historic Preservation Graduate School of Architecture, Planning and Preservation Columbia University May 2014 2 Abstract What’s On the Surface Does Matter: The Conservation of Applied Surface Decoration of Historic Stained Glass Windows Alyssa Grieco Advisor: George Wheeler A stained glass window is both an architectural building element and an individual work of art. Like architecture, a stained glass window is composed of a variety of materials, mainly glass, lead, and surface decoration, each of which has its own conservation issues. Surface decoration, which includes vitreous glass paint, silver stain, and enamels, is the component of a stained glass window that is sometimes underappreciated. While it may not pose a major threat to the physical stability of the window or the safety of the window’s environment, it is the decoration that defines the windows as works of art, with imagery that holds the window’s history, including a direct view into the traditions, ideals, and beliefs of the people of their time. The conservation of the surface decoration of stained glass windows has never been fully analyzed, and both glazing and conservation professionals are constantly seeking information regarding the history of the materials and techniques used in order to create or restore a stained glass window. With conservation, the methods and techniques used to maintain and conserve the decoration will vary depending on a number of circumstances, including the location of the window, the history and traditions of the people involved, and the tools available to the conservators.
    [Show full text]
  • Bulletin of the United States Bureau of Labor Statistics, No
    U. S. DEPARTMENT OF LABOR JAMES J. DAVIS, Secretary BUREAU OF LABOR STATISTICS ETHELBERT STEWART, Commissioner BULLETIN OF THE UNITED STATES ) BUREAU OF LABOR STATISTICS \ # * • No. 441 PRODUCTIVITY OF LABOR SERIES PRODUCTIVITY OF LABOR IN THE GLASS INDUSTRY / v \ \ “ / JULY, 1927 UNITED STATES GOVERNMENT PRINTING OFFICE WASHINGTON 1927 Digitized for FRASER http://fraser.stlouisfed.org/ Federal Reserve Bank of St. Louis ACKNOWLEDGMENT This bulletin was prepared by Boris Stern, of the United States Bureau of Labor Statistics. ii ADDITIONAL COPIES OF THIS PUBLICATION MAY BE PROCURED FROM THE SUPERINTENDENT OF DOCUMENTS U .S . GOVERNMENT PRINTING OFFICE WASHINGTON, D. C. AT 40 CENTS PER COPY Digitized for FRASER http://fraser.stlouisfed.org/ Federal Reserve Bank of St. Louis CONTENTS Introduction and summary: Page Industrial revolution in the glass industry____________________ ____ 1-14 Early history of glass making_______________________________ 1-3 Regenerative furnace and continuous tank___________________ 3, 4 Development of machinery in the industry___________________ 4-7 Bottles and jars_______________________________________ 4, 5 Pressed ware__________________________________________ 5 Blown ware___________________________________________ 5, 6 Window glass__________________________________________ 6 Plate glass____________________________________________ 6, 7 Effects of machinery on labor productivity and labor cost_____ 7-14 Bottles and jars________________________________________ 7, 8 Pressed ware__________________________________________
    [Show full text]
  • M. Georges Bontemps (1799-1884), Directeur De Choisy-Le-Roi Nekrolog Von M
    Pressglas-Korrespondenz 2010-2 M. Georges Bontemps (1799-1884), Directeur de Choisy-le-Roi Nekrolog von M. Eugène-Melchior Péligot Moniteur de la Céramique et de la Verrerie, Verlag Edmond Rousset, Paris, 1. Okt. 1884, S. 224 Zur Verfügung gestellt von Herrn Dieter Neumann. Herzlichen Dank! [Übersetzung aus dem Französischen SG] das Verfahren der Mischung dieses Glases [brassage du verre] kennt, das von seinem Vater erfunden wurde, und Nekrolog - Notiz von M. Peligot [Eugène- an M. Bontemps, der dieses Verfahren und das Produkt Melchior Péligot], Sekretär du Conseil, in Choisy-le-Roi bei umfangreichen Mengen von Flint- über M. George Bontemps, glas verbessert hatte. Ein weiterer Preis von 4.000 Franc ehemals Direktor von Choisy-le-Roi wurde zwischen zwei Gesellschaftern der Fabrik für Der Dekan der französischen Glasmeister [doyen des Flintglas aufgeteilt. verriers français] M. Georges Bontemps ist nach einer Auf der „Exposition des produits de l'industrie nationa- kurzen Krankheit in Amboise verstorben. 1799 geboren, le“ von 1839 hat M. Bontemps eine neue Goldmedaille trat M. Bontemps mit siebzehn Jahren [1816] in das Po- empfangen. „Wenige Hersteller“, sagt M. Dumas in sei- lytechnikum [Ecole polytechnique] ein; in dieser Schule nem Bericht, haben „diese Liebe zu ihrer Kunst in glei- erwarb er die wissenschaftlichen Kenntnisse, die einen chem Maße, die sie dazu bringt, alle ihre Aspekte anzu- so fruchtbaren Einfluss auf seine industrielle Karriere visieren und sich um alle ihre Äste zu kümmern.“ Bon- ausgeübt haben. temps wurde auf der Ausstellung von 1844 dekoriert; Zuerst beschäftigt in der Cristallerie de Baccarat, die und er war internationaler Preisrichter auf den Weltaus- 1818 [1816!] von d’Artigues erworben wurde, wurde stellungen von 1862 und 1867.
    [Show full text]
  • Vidro Laminado
    8. GLASSES M. Clara Gonçalves Departamento de Engenharia de Química Instituto Superior Técnico Universidade de Lisboa Av. Rovisco Pais, 1049-001 Lisboa, Portugal Tel.: 351 21 8419934 Fax: 351 21 8418132 E-mail: [email protected] Abstract In architecture, glass established itself as an element that provided cohesion between the inside and the outside. Glass is a transparent structural material and one of the few building materials that combines tradition with technological innovation. Glass is a product that harmonizes colour, reflectance, transparency or opacity, texture and thickness, flatness or curvature with, for example, some control over opacity or self- cleaning properties, whilst at the same time being low-emissive, heat and/or sound insulator, offers protection and security, as well as resistance to thermal shock and impact from projectiles. Moreover glass is the only material that is 100% recyclable, what we should bear in mind, as sustainable development is only possible by careful use of resources and technology. Glass is, definitively, a hard product to beat. Outline 1. Glass in construction and architecture: brief history 2. Glass composition and structure 2.1 What is glass? 2.2.1 Zachariasen rules or crystallochemical theory 2.2 Raw materials 3. Glass technology 3.1 Melting, homogenization and fining 3.2 Flat glass forming techniques 3.2.1 Roman glass 3.2.2 Medieval glass 1 3.2.3 Crown glass 3.2.4 Colburn-Libbey-Owens Glass 3.2.5 Fourcault-Pittsburgh glass 3.2.6 Float glass 3.3 Annealing 3.4 Flow chart of float glass production process 4.
    [Show full text]
  • GPC18 Final Program.Indd
    GPC is the largest glass manufacturing event in North America, attracting global manufacturers and suppliers to exchange innovations and solutions. 79 where glass manufacturers meet November 5 – 8, 2018 Greater Columbus Convention Center Columbus, Ohio USA CONFERENCE GUIDE Gold Sponsor Organized by: Endorsed by: Tri-Mer World Leader in Glass Emissions Control Greater Columbus Convention Center | Columbus, Ohio USA More installed systems than all other suppliers combined Nearly a decade in glass: container, flat glass, tableware The proven solution for air-fuel and oxy-fuel gas furnace emissions: PM, NOx, SOx, HCl, HF, metals, mercury, hex chrome, dioxins/furans, VOCs, CO Talk with Technical Sales Director Kevin Moss, Booth 305, or call 989-321-2991 www.tri-mer.com 2 including Asset Durability and Cost Control for Glass Manufacturing Furnaces 79November 5 – 8, 2018 Greater Columbus Convention Center | Columbus, Ohio USA Welcome to the 79th Conference on Glass Problems (GPC), which is devoted to glass manufacturing, an industry whose products are as essenti al as they are ubiquitous. It’s fi tti ng that the scope of this conference is equally extensive, covering a wide range of industry interests. The Glass Manufacturing Industry Council (GMIC), the leading trade associati on bridging glass segments, in partnership with Alfred University, the leading American glass teaching and research insti tuti on, co-organize the conference, with programming directi on provided by an industry advisory board. Bob Lipetz, MBA GPC technical sessions address manufacturing issues, citi ng real world data from manufacturers and soluti ons Conference Director Glass Manufacturing Industry Council providers. Additi onal value-rich resources are available, such as our two short courses on Combusti on and on Fundamentals of Batch and Furnace Operati ons.
    [Show full text]