DOCSLIB.ORG

Measure Theory 1 Measurable Spaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measure Theory 1 Measurable Spaces Measure Theory 1 Measurable Spaces A measurable space is a set S, together with a nonempty collection, , of subsets of S, satisfying the following two conditions: S 1. For any A; B in the collection , the set1 A B is also in . S − S 2. For any A1; A2; , Ai . The elements of ·are· · 2calledS [measurable2 S sets. These two conditions are S summarized by saying that the measurable sets are closed under taking finite differences and countable unions. Think of S as the arena in which all the action (integrals, etc) will take place; and of the measurable sets are those that are \candidates for having a size". In some examples, all the measurable sets will be assigned a \size"; in others, only the smaller measurable sets will be (with the remaining mea- surable sets having, effectively “infinite size"). Several properties of measurable sets are immediate from the definition. 1. The empty set, , is measurable. [Since is nonempty, there exists some measurable set A.;So, A A = is measurable,S by condition 1 above.] − ; 2. For A and B any two measurable sets, A B, A B, and A B are all measurable. [The third is just condition 1\above.[For the second,− apply condition 2 to the sequence A; B; ; ; . For the first, note that ; ; · · · A B = A (A B): Use condition 1 twice.] It follows immediately, by rep\eated application− − of these facts, that the measurable sets are closed under taking any finite numbers of intersections, unions, and differences. 3. For A1; A2; measurable, their intersection, A , is also measurable. · · · \ i [First note that we have the following set-theoretic identity: A1 A2 A3 \ \ \ = A1 (A1 A2) (A1 A3) (A1 A4) . Now, on the right, apply· · · condition− f 1−above[to the−set-differences,[ − and[condition· · ·g 2 to the union.] Thus, measurable sets are closed under taking countable intersections and unions. Here are some examples of measurable spaces. 1. Let S be any set, and let consist only of the empty set . This is a S ; (rather boring) measurable space. 1By A B, we mean A Bc, i.e., the set of all points of A that are not in B. − \ 1 2. Let S be any set, and let consist of all subsets of S. This is a measurable space. S 3. Let S be any set, and let consist of all subsets of S that are countable (or finite). This is a measurableS space. 4. Let S be any set, and fix any nonempty collection of subsets of P S. Let be the collection of subsets of S that result from the following construction.S First set = . Now expand to include all sets that result S P S by taking differences and countable unions of sets in . Next, again expand to include all sets that result by taking differencesSand countable unions ofS sets in (the already expanded) . Continue in this way2, and denote by S S the collection that results. Then (S; ) is a measurable space. Thus, you can generate measurable spaces by startingS with any set S, and any collection of subsets of S (i.e., those that you really want to turn out, in the end, toP be measurable). By expanding that original collection , as described above, you can indeed achieve a measurable space in whichPthe chosen sets are indeed measurable. 5. Let (S; ) be any measurable space, and let K S (not necessar- ily measurable).S Let denote the collection of all subsets⊂ of K that are K -measurable. Then (K; ) is a measurable space. [The two properties forS (K; ) follow immediatelyK from the corresponding properties of (S; ).] K S Thus, each subset of a measurable space gives rise to a new measurable space (called a subspace of the original measurable space). 6. Let (S0; 0) and (S00; 00) be measurable spaces, based on disjoint un- S 0 S00 derlying sets. Set S = S S , and let consist of all sets A S such that A S0 0 and A S00 [ 00. ThenS(S; ) is a measurable⊂space. [The \ 2 S \ 2 S S two properties for (S; ) follow immediately from the corresponding prop- erties of (S0; 0) and (SS00; 00). For instance, the first property follows from: (A B) S0 S= (A S0) S(B S0) and (A B) S00 = (A S00) (B S00).] − \ \ − \ − \ \ − \ 2 Measures Let (S; ) be a measurable space. A measure on (S; ) consists of a S µS nonempty subset, , of , together with a mapping R+ (where R+ M S M ! 2 In more detail: Set 1 = . Let 2 the set that results from applying the above S P S process to 1; then by 3 the set that results from applying the process to 2, etc. Then S S S set = 1 2 . S S [ S [ · · · 2 denotes the set of nonnegative reals), satisfying the following two conditions: 1. For any A and any B A, with B , we have B . 2 M ⊂ 2 S 2 M 2. Let A1; A2; be disjoint, and set A = A1 A2 . Then: This · · · 2 M [ [· · · union A is in if and only if the sum µ(A1) + µ(A2) + converges; and when these holdMthat sum is precisely µ(A). · · · A set A is said to have measure; and µ(A) is called the measure of A. Think2ofMthe collection as consisting of those measurable sets that M actually are assigned a \size" (i.e., of those size-candidates (in ) that were successful); and of µ(A) as that size. Then the first condition abSove says that all sufficiently small measurable sets are indeed assigned size. The second condition says that the only excuse a measurable set A has for not being assigned a size is that \there is already too much measure inside A", i.e., that A effectively has “infinite measure". The last part of condition 2 says that measure is additive under taking unions of disjoint sets (something we would have wanted and expected to be true). Several properties of measures are immediate from the definition. 1. The empty set is in , and µ( ) = 0. [There exists some set A . Set B = and apply;conditionM 1, to conclude; . Now apply condition2 M ; ; 2 M 2 to the sequence ; ; (having union A = ). Since A , we have µ( ) + µ( ) + =;µ;( ·),· ·which implies µ( ) = 0.]; 2 M ; ; · · · ; ; 2. For any A; B , A B, A B, and A B are all in . Furthermore, if A and B are disjoin2 Mt, then\ µ(A [ B) = µ(A−) + µ(B). [TheM first and third follow immediately from condition[1, since A B and A B are both subsets \ − of A. For the second, apply condition 2 to the sequence A B; B; ; ; of disjoint sets, with union A B. Additivity of the measures−also follo; ws; ·from· · [ this, since when A and B are disjoint, A B = A.] 3. For any A; B , with B A,−then µ(B) µ(A). [We have, by the previous item, µ(2A)M= µ(B) + µ⊂(A B).] Thus, \the≤ bigger the set, the − larger its measure". 4. For any A1; A2; , A . [This is immediate from condition · · · 2 M \ i 2 M 1 above, since A and A A1 .] \ i 2 S \ i ⊂ 2 M Thus, the sets that have measure (i.e., those that are in ) are closed under finite differences, intersections and unions; as well as underM countable intersections. What about countable unions? Let A1; A2; be a sequence of sets in , not necessarily disjoint. First note that A =· ·A· can always be M [ i written as a union of a collection of disjoint sets in , namely of A1; A2 M − A1; A3 A2 A1; . If the sum of the measures of the sets in this last list − − · · · 3 converges, then, by condition 2 above, we are guaranteed that A . And if the sum doesn't converge, then we are guaranteed that A is not 2inM . Note, M incidentally, that convergence of this sum is guaranteed by convergence of the sum µ(A1) + µ(A2) + µ(A3) + (but, without disjointness, this last sum may exceed µ(A)). In short, the·sets· · that have measure are not in general closed under countable unions, but failure occurs only because of excessive measure. Here are some examples of measures. 1. Let S be any set, let , the collection of measurable sets, be all subsets of S, let = , and, for AS , let µ(A) = 0. This is a (boring) measure. M S 2 M 2. Let S be any set, all countable (or finite) subsets of S, the collection of all finite subsetsS of S, and, for A , let µ(A) be the nMumber 2 M of elements in the set A. This is is called counting measure on S. Note that the set S itself could be uncountable. 3. Let S be any set and the collection of all subsets of S. Fix a f S nonnegative function S R+ on S. Now let consist of all sets A such that Σ f converges.! Thus, includes allMthe finite subsets of S; 2andS A M possibly some countably infinite subsets (provided there isn't too much f on the subset); and possibly even some uncountable infinite subsets (provided f vanishes a lot on the subset). For A , set µ(A) = ΣAf. This is a measure. For f = 1, it reduces to counting2 measure.M 4. Let (S; ; ; µ) be any measurable space/measure. Fix any K S S M 2 (not necessarily in ). Denote by the collection of all sets in that are subsets of K; and bSy the collectionK of all sets in that areSsubsets of MK M K.
Load more

Recommended publications
  • Measure-Theoretic Probability I
    Measure-Theoretic Probability I Steven P.Lalley Winter 2017 1 1 Measure Theory 1.1 Why Measure Theory? There are two different views – not necessarily exclusive – on what “probability” means: the subjectivist view and the frequentist view. To the subjectivist, probability is a system of laws that should govern a rational person’s behavior in situations where a bet must be placed (not necessarily just in a casino, but in situations where a decision must be made about how to proceed when only imperfect information about the outcome of the decision is available, for instance, should I allow Dr. Scissorhands to replace my arthritic knee by a plastic joint?). To the frequentist, the laws of probability describe the long- run relative frequencies of different events in “experiments” that can be repeated under roughly identical conditions, for instance, rolling a pair of dice. For the frequentist inter- pretation, it is imperative that probability spaces be large enough to allow a description of an experiment, like dice-rolling, that is repeated infinitely many times, and that the mathematical laws should permit easy handling of limits, so that one can make sense of things like “the probability that the long-run fraction of dice rolls where the two dice sum to 7 is 1/6”. But even for the subjectivist, the laws of probability should allow for description of situations where there might be a continuum of possible outcomes, or pos- sible actions to be taken. Once one is reconciled to the need for such flexibility, it soon becomes apparent that measure theory (the theory of countably additive, as opposed to merely finitely additive measures) is the only way to go.
    [Show full text]
  • Hausdorff Measure
    Hausdorff Measure Jimmy Briggs and Tim Tyree December 3, 2016 1 1 Introduction In this report, we explore the the measurement of arbitrary subsets of the metric space (X; ρ); a topological space X along with its distance function ρ. We introduce Hausdorff Measure as a natural way of assigning sizes to these sets, especially those of smaller \dimension" than X: After an exploration of the salient properties of Hausdorff Measure, we proceed to a definition of Hausdorff dimension, a separate idea of size that allows us a more robust comparison between rough subsets of X. Many of the theorems in this report will be summarized in a proof sketch or shown by visual example. For a more rigorous treatment of the same material, we redirect the reader to Gerald B. Folland's Real Analysis: Modern techniques and their applications. Chapter 11 of the 1999 edition served as our primary reference. 2 Hausdorff Measure 2.1 Measuring low-dimensional subsets of X The need for Hausdorff Measure arises from the need to know the size of lower-dimensional subsets of a metric space. This idea is not as exotic as it may sound. In a high school Geometry course, we learn formulas for objects of various dimension embedded in R3: In Figure 1 we see the line segment, the circle, and the sphere, each with it's own idea of size. We call these length, area, and volume, respectively. Figure 1: low-dimensional subsets of R3: 2 4 3 2r πr 3 πr Note that while only volume measures something of the same dimension as the host space, R3; length, and area can still be of interest to us, especially 2 in applications.
    [Show full text]
  • Caratheodory's Extension Theorem
    Caratheodory’s extension theorem DBW August 3, 2016 These notes are meant as introductory notes on Caratheodory’s extension theorem. The presentation is not completely my own work; the presentation heavily relies on the pre- sentation of Noel Vaillant on http://www.probability.net/WEBcaratheodory.pdf. To make the line of arguments as clear as possible, the starting point is the notion of a ring on a topological space and not the notion of a semi-ring. 1 Elementary definitions and properties We fix a topological space Ω. The power set of Ω is denoted P(Ω) and consists of all subsets of Ω. Definition 1. A ring on on Ω is a subset R of P(Ω), such that (i) ∅ ∈ R (ii) A, B ∈ R ⇒ A ∪ B ∈ R (iii) A, B ∈ R ⇒ A \ B ∈ R Definition 2. A σ-algebra on Ω is a subset Σ of P(Ω) such that (i) ∅ ∈ Σ (ii) (An)n∈N ∈ Σ ⇒ ∪n An ∈ Σ (iii) A ∈ Σ ⇒ Ac ∈ Σ Since A∩B = A\(A\B) it follows that any ring on Ω is closed under finite intersections; c c hence any ring is also a semi-ring. Since ∩nAn = (∪nA ) it follows that any σ-algebra is closed under arbitrary intersections. And from A \ B = A ∩ Bc we deduce that any σ-algebra is also a ring. If (Ri)i∈I is a set of rings on Ω then it is clear that ∩I Ri is also a ring on Ω. Let S be any subset of P(Ω), then we call the intersection of all rings on Ω containing S the ring generated by S.
    [Show full text]
  • (Measure Theory for Dummies) UWEE Technical Report Number UWEETR-2006-0008
    A Measure Theory Tutorial (Measure Theory for Dummies) Maya R. Gupta {gupta}@ee.washington.edu Dept of EE, University of Washington Seattle WA, 98195-2500 UWEE Technical Report Number UWEETR-2006-0008 May 2006 Department of Electrical Engineering University of Washington Box 352500 Seattle, Washington 98195-2500 PHN: (206) 543-2150 FAX: (206) 543-3842 URL: http://www.ee.washington.edu A Measure Theory Tutorial (Measure Theory for Dummies) Maya R. Gupta {gupta}@ee.washington.edu Dept of EE, University of Washington Seattle WA, 98195-2500 University of Washington, Dept. of EE, UWEETR-2006-0008 May 2006 Abstract This tutorial is an informal introduction to measure theory for people who are interested in reading papers that use measure theory. The tutorial assumes one has had at least a year of college-level calculus, some graduate level exposure to random processes, and familiarity with terms like “closed” and “open.” The focus is on the terms and ideas relevant to applied probability and information theory. There are no proofs and no exercises. Measure theory is a bit like grammar, many people communicate clearly without worrying about all the details, but the details do exist and for good reasons. There are a number of great texts that do measure theory justice. This is not one of them. Rather this is a hack way to get the basic ideas down so you can read through research papers and follow what’s going on. Hopefully, you’ll get curious and excited enough about the details to check out some of the references for a deeper understanding.
    [Show full text]
  • Measure Theory and Probability
    Measure theory and probability Alexander Grigoryan University of Bielefeld Lecture Notes, October 2007 - February 2008 Contents 1 Construction of measures 3 1.1Introductionandexamples........................... 3 1.2 σ-additive measures ............................... 5 1.3 An example of using probability theory . .................. 7 1.4Extensionofmeasurefromsemi-ringtoaring................ 8 1.5 Extension of measure to a σ-algebra...................... 11 1.5.1 σ-rings and σ-algebras......................... 11 1.5.2 Outermeasure............................. 13 1.5.3 Symmetric difference.......................... 14 1.5.4 Measurable sets . ............................ 16 1.6 σ-finitemeasures................................ 20 1.7Nullsets..................................... 23 1.8 Lebesgue measure in Rn ............................ 25 1.8.1 Productmeasure............................ 25 1.8.2 Construction of measure in Rn. .................... 26 1.9 Probability spaces ................................ 28 1.10 Independence . ................................. 29 2 Integration 38 2.1 Measurable functions.............................. 38 2.2Sequencesofmeasurablefunctions....................... 42 2.3 The Lebesgue integral for finitemeasures................... 47 2.3.1 Simplefunctions............................ 47 2.3.2 Positivemeasurablefunctions..................... 49 2.3.3 Integrablefunctions........................... 52 2.4Integrationoversubsets............................ 56 2.5 The Lebesgue integral for σ-finitemeasure.................
    [Show full text]
  • Construction of Geometric Outer-Measures and Dimension Theory
    Construction of Geometric Outer-Measures and Dimension Theory by David Worth B.S., Mathematics, University of New Mexico, 2003 THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science Mathematics The University of New Mexico Albuquerque, New Mexico December, 2006 c 2008, David Worth iii DEDICATION To my lovely wife Meghan, to whom I am eternally grateful for her support and love. Without her I would never have followed my education or my bliss. iv ACKNOWLEDGMENTS I would like to thank my advisor, Dr. Terry Loring, for his years of encouragement and aid in pursuing mathematics. I would also like to thank Dr. Cristina Pereyra for her unfailing encouragement and her aid in completing this daunting task. I would like to thank Dr. Wojciech Kucharz for his guidance and encouragement for the entirety of my adult mathematical career. Moreover I would like to thank Dr. Jens Lorenz, Dr. Vladimir I Koltchinskii, Dr. James Ellison, and Dr. Alexandru Buium for their years of inspirational teaching and their influence in my life. v Construction of Geometric Outer-Measures and Dimension Theory by David Worth ABSTRACT OF THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science Mathematics The University of New Mexico Albuquerque, New Mexico December, 2006 Construction of Geometric Outer-Measures and Dimension Theory by David Worth B.S., Mathematics, University of New Mexico, 2003 M.S., Mathematics, University of New Mexico, 2008 Abstract Geometric Measure Theory is the rigorous mathematical study of the field commonly known as Fractal Geometry. In this work we survey means of constructing families of measures, via the so-called \Carath´eodory construction", which isolate certain small- scale features of complicated sets in a metric space.
    [Show full text]
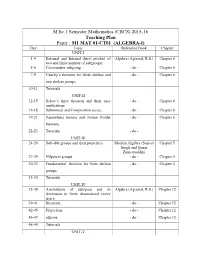
  • M.Sc. I Semester Mathematics (CBCS) 2015-16 Teaching Plan
    M.Sc. I Semester Mathematics (CBCS) 2015-16 Teaching Plan Paper : M1 MAT 01-CT01 (ALGEBRA-I) Day Topic Reference Book Chapter UNIT-I 1-4 External and Internal direct product of Algebra (Agrawal, R.S.) Chapter 6 two and finite number of subgroups; 5-6 Commutator subgroup - do - Chapter 6 7-9 Cauchy’s theorem for finite abelian and - do - Chapter 6 non abelian groups. 10-11 Tutorials UNIT-II 12-15 Sylow’s three theorem and their easy - do - Chapter 6 applications 16-18 Subnormal and Composition series, - do - Chapter 6 19-21 Zassenhaus lemma and Jordan Holder - do - Chapter 6 theorem. 22-23 Tutorials - do - UNIT-III 24-26 Solvable groups and their properties Modern Algebra (Surjeet Chapter 5 Singh and Quazi Zameeruddin) 27-29 Nilpotent groups - do - Chapter 5 30-32 Fundamental theorem for finite abelian - do - Chapter 4 groups. 33-34 Tutorials UNIT-IV 35-38 Annihilators of subspace and its Algebra (Agrawal, R.S.) Chapter 12 dimension in finite dimensional vector space 39-41 Invariant, - do - Chapter 12 42-45 Projection, - do - Chapter 12 46-47 adjoins. - do - Chapter 12 48-49 Tutorials UNIT-V 50-54 Singular and nonsingular linear Algebra (Agrawal, R.S.) Chapter 12 transformation 55-58 quadratic forms and Diagonalization. - do - Chapter12 59-60 Tutorials - do - 61-65 Students Interaction & Difficulty solving - - M.Sc. I Semester Mathematics (CBCS) 2015-16 Teaching Plan Paper : M1 MAT 02-CT02 (REAL ANALYSIS) Day Topic Reference Book Chapter UNIT-I 1-2 Length of an interval, outer measure of a Theory and Problems of Chapter 2 subset of R, Labesgue outer measure of a Real Variables: Murray subset of R R.
    [Show full text]
  • Section 17.5. the Carathéodry-Hahn Theorem: the Extension of A
    17.5. The Carath´eodory-Hahn Theorem 1 Section 17.5. The Carath´eodry-Hahn Theorem: The Extension of a Premeasure to a Measure Note. We have µ defined on S and use µ to define µ∗ on X. We then restrict µ∗ to a subset of X on which µ∗ is a measure (denoted µ). Unlike with Lebesgue measure where the elements of S are measurable sets themselves (and S is the set of open intervals), we may not have µ defined on S. In this section, we look for conditions on µ : S → [0, ∞] which imply the measurability of the elements of S. Under these conditions, µ is then an extension of µ from S to M (the σ-algebra of measurable sets). ∞ Definition. A set function µ : S → [0, ∞] is finitely additive if whenever {Ek}k=1 ∞ is a finite disjoint collection of sets in S and ∪k=1Ek ∈ S, we have n n µ · Ek = µ(Ek). k=1 ! k=1 [ X Note. We have previously defined finitely monotone for set functions and Propo- sition 17.6 gives finite additivity for an outer measure on M, but this is the first time we have discussed a finitely additive set function. Proposition 17.11. Let S be a collection of subsets of X and µ : S → [0, ∞] a set function. In order that the Carath´eodory measure µ induced by µ be an extension of µ (that is, µ = µ on S) it is necessary that µ be both finitely additive and countably monotone and, if ∅ ∈ S, then µ(∅) = 0.
    [Show full text]
  • Measure and Integration
    ¦ Measure and Integration Man is the measure of all things. — Pythagoras Lebesgue is the measure of almost all things. — Anonymous ¦.G Motivation We shall give a few reasons why it is worth bothering with measure the- ory and the Lebesgue integral. To this end, we stress the importance of measure theory in three different areas. ¦.G.G We want a powerful integral At the end of the previous chapter we encountered a neat application of Banach’s fixed point theorem to solve ordinary differential equations. An essential ingredient in the argument was the observation in Lemma 2.77 that the operation of differentiation could be replaced by integration. Note that differentiation is an operation that destroys regularity, while in- tegration yields further regularity. It is a consequence of the fundamental theorem of calculus that the indefinite integral of a continuous function is a continuously differentiable function. So far we used the elementary notion of the Riemann integral. Let us quickly recall the definition of the Riemann integral on a bounded interval. Definition 3.1. Let [a, b] with −¥ < a < b < ¥ be a compact in- terval. A partition of [a, b] is a finite sequence p := (t0,..., tN) such that a = t0 < t1 < ··· < tN = b. The mesh size of p is jpj := max1≤k≤Njtk − tk−1j. Given a partition p of [a, b], an associated vector of sample points (frequently also called tags) is a vector x = (x1,..., xN) such that xk 2 [tk−1, tk]. Given a function f : [a, b] ! R and a tagged 51 3 Measure and Integration partition (p, x) of [a, b], the Riemann sum S( f , p, x) is defined by N S( f , p, x) := ∑ f (xk)(tk − tk−1).
    [Show full text]
  • An Approximate Logic for Measures
    AN APPROXIMATE LOGIC FOR MEASURES ISAAC GOLDBRING AND HENRY TOWSNER Abstract. We present a logical framework for formalizing connections be- tween finitary combinatorics and measure theory or ergodic theory that have appeared in various places throughout the literature. We develop the basic syntax and semantics of this logic and give applications, showing that the method can express the classic Furstenberg correspondence as well as provide short proofs of the Szemer´edi Regularity Lemma and the hypergraph removal lemma. We also derive some connections between the model-theoretic notion of stability and the Gowers uniformity norms from combinatorics. 1. Introduction Since the 1970’s, diagonalization arguments (and their generalization to ul- trafilters) have been used to connect results in finitary combinatorics with results in measure theory or ergodic theory [14]. Although it has long been known that this connection can be described with first-order logic, a recent striking paper by Hrushovski [22] demonstrated that modern developments in model theory can be used to give new substantive results in this area as well. Papers on various aspects of this interaction have been published from a va- riety of perspectives, with almost as wide a variety of terminology [30, 10, 9, 1, 32, 13, 4]. Our goal in this paper is to present an assortment of these techniques in a common framework. We hope this will make the entire area more accessible. We are typically concerned with the situation where we wish to prove a state- ment 1) about sufficiently large finite structures which 2) concerns the finite analogs of measure-theoretic notions such as density or integrals.
    [Show full text]
  • Notes on Ergodic Theory
    Notes on ergodic theory Michael Hochman1 January 27, 2013 1Please report any errors to [email protected] Contents 1 Introduction 4 2 Measure preserving transformations 6 2.1 Measure preserving transformations . 6 2.2 Recurrence . 9 2.3 Inducedactiononfunctionsandmeasures . 11 2.4 Dynamics on metric spaces . 13 2.5 Some technicalities . 15 3 Ergodicity 17 3.1 Ergodicity . 17 3.2 Mixing . 19 3.3 Kac’s return time formula . 20 3.4 Ergodic measures as extreme points . 21 3.5 Ergodic decomposition I . 23 3.6 Measure integration . 24 3.7 Measure disintegration . 25 3.8 Ergodic decomposition II . 28 4 The ergodic theorem 31 4.1 Preliminaries . 31 4.2 Mean ergodic theorem . 32 4.3 Thepointwiseergodictheorem . 34 4.4 Generic points . 38 4.5 Unique ergodicity and circle rotations . 41 4.6 Sub-additive ergodic theorem . 43 5 Some categorical constructions 48 5.1 Isomorphismandfactors. 48 5.2 Product systems . 52 5.3 Natural extension . 53 5.4 Inverselimits ............................. 53 5.5 Skew products . 54 1 CONTENTS 2 6 Weak mixing 56 6.1 Weak mixing . 56 6.2 Weak mixing as a multiplier property . 59 6.3 Isometricfactors ........................... 61 6.4 Eigenfunctions . 62 6.5 Spectral isomorphism and the Kronecker factor . 66 6.6 Spectral methods . 68 7 Disjointness and a taste of entropy theory 73 7.1 Joinings and disjointness . 73 7.2 Spectrum, disjointness and the Wiener-Wintner theorem . 75 7.3 Shannon entropy: a quick introduction . 77 7.4 Digression: applications of entropy . 81 7.5 Entropy of a stationary process .
    [Show full text]
  • 2.5 Outer Measure and Measurable Sets. Note the Results of This Section Concern Any Given Outer Measure Λ
    2.5 Outer Measure and Measurable sets. Note The results of this section concern any given outer measure ¸. If an outer measure ¸ on a set X were a measure then it would be additive. In particular, given any two sets A; B ⊆ X we have that A \ B and A \ Bc are disjoint with (A \ B) [ (A \ Bc) = A and so we would have ¸(A) = ¸(A \ B) + ¸(A \ Bc): We will see later that this does not necessarily hold for all A and B but it does lead to the following definition. Definition Let ¸ be an outer measure on a set X. Then E ⊆ X is said to be measurable with respect to ¸ (or ¸-measurable) if ¸(A) = ¸(A \ E) + ¸(A \ Ec) for all A ⊆ X. (7) (This can be read as saying that we take each and every possible “test set”, A, look at the measures of the parts of A that fall within and without E, and check whether these measures add up to that of A.) Since ¸ is subadditive we have ¸(A) · ¸(A\E)+¸(A\Ec) so, in checking measurability, we need only verify that ¸(A) ¸ ¸(A \ E) + ¸(A \ Ec) for all A ⊆ X. (8) Let M = M(¸) denote the collection of ¸-measurable sets. Theorem 2.6 M is a field. Proof Trivially Á and X are in M. Take any E1;E2 2 M and any test set A ⊆ X. Then c ¸(A) = ¸(A \ E1) + ¸(A \ E1): c Now apply the definition of measurability for E2 with the test set A \ E1 to get c c c c ¸(A \ E1) = ¸((A \ E1) \ E2) + ¸((A \ E1) \ E2) c c = ¸(A \ E1 \ E2) + ¸(A \ (E1 [ E2) ): Combining c c ¸(A) = ¸(A \ E1) + ¸(A \ E1 \ E2) + ¸(A \ (E1 [ E2) ): (9) 1 We hope to use the subadditivity of ¸ on the first two term on the right hand side of (9).
    [Show full text]