DOCSLIB.ORG

2.1.3 Outer Measures and Construction of Measures Recall the Construction of Lebesgue Measure on the Real Line

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2.1.3 Outer Measures and Construction of Measures Recall the Construction of Lebesgue Measure on the Real Line CHAPTER 2. THE LEBESGUE INTEGRAL I 11 2.1.3 Outer measures and construction of measures Recall the construction of Lebesgue measure on the real line. There are various approaches to construct the Lebesgue measure on the real line. For example, consider the collection of finite union of sets of the form ]a; b]; ] − 1; b]; ]a; 1[ R: This collection is an algebra A but not a sigma-algebra (this has been discussed on p.7). A natural measure on A is given by the length of an interval. One attempts to measure the size of any subset S of R covering it by countably many intervals (recall also that R can be covered by countably many intervals) and we define this quantity by 1 1 X [ m∗(S) = inff jAkj : Ak 2 A;S ⊂ Akg (2.7) k=1 k=1 where jAkj denotes the length of the interval Ak. However, m∗(S) is not a measure since it is not additive, which we do not prove here. It is only sigma- subadditive, that is k k [ X m∗ Sn ≤ m∗(Sn) n=1 n=1 for any countable collection (Sn) of subsets of R. Alternatively one could choose coverings by open intervals (see the exercises, see also B.Dacorogna, Analyse avanc´eepour math´ematiciens)Note that the quantity m∗ coincides with the length for any set in A, that is the measure on A (this is surprisingly the more difficult part!). Also note that the sigma-subadditivity implies that m∗(A) = 0 for any countable set since m∗(fpg) = 0 for any p 2 R. In order to get a measure from m∗ one then restricts m∗(S) to a smaller class of subsets which forms a sigma-algebra and contains A where it has the desired property of sigma-additivity. In the following we describe this procedure in an abstract setting. Definition - outer measure. Let Ω be a nonempty set. An outer measure is a set function m∗ : P(Ω) ! R+ [ f1g satisfying the following conditions: m∗(;) = 0 (2.8) A ⊂ B ) m∗(A) ≤ m∗(B) (2.9) 1 1 [ X m∗ An ≤ m∗(An): (2.10) n=1 n=1 For example, m∗ given by (2.7) is an outer measure on P(R). We shall show in the theorem below that in an appropriate abstract setting the set functions as defined by (2.7) are always outer measures. Note, that a covering by a finite number of intervals or more generally cubes or rectangles which gives rise to so called outer Jordan content will not suffice in the definition of an outer measure. For example, the rational numbers in [0; 1] have outer Jordan content 1 but the outer measure m∗ is zero since the outer measure of a single point is equal to zero and the rational numbers are countable. CHAPTER 2. THE LEBESGUE INTEGRAL I 12 Construction of an outer measure from a pre-measure defined on an algebra. Let A ⊂ P(Ω) an algebra. Suppose there is a function m0 : A! R [ f1g with the following properties: 1. m0(;) = 0, S 2. if A = k≥1 Ak 2 A for some countable collection of disjoint Ak 2 A, then X m0(A) = m0(Ak): k≥1 Such a function is called a pre-measure. In many applications we also have the S property that Ω = k≥1 Ak for some countable collection of disjoint Ak 2 A. If m0(Ak) < 1 for all k we call m0 a sigma-finite pre-measure. If m0(Ω) < 1 we call m0 a finite pre-measure. For any S ⊂ Ω define 1 1 X [ m∗(S) = inff m0(Ak): Ak 2 A;S ⊂ Akg: (2.11) k=1 k=1 Theorem. m∗ is an outer measure and m∗(A) = m0(A) for any A 2 A. Proof. Obviously m∗(;) = 0 and if A ⊂ B, then any covering of B is also a covering of A. Hence m∗(A) ≤ m∗(B). In order to prove the sigma-subadditivity let > 0 be arbitrary. We choose for each Ak a covering Ckn 2 A such that 1 1 [ X −k Ak ⊂ Ckn; m0(Ckn) ≤ m∗(Ak) + 2 . n=1 n=1 S1 Now fCkn; k 2 Z+; n 2 Z+g is a countable covering of k=1 Ak by elements of A and therefore it follows from the definition of m∗ that 1 1 1 1 1 [ X X X −k X m∗ Ak ≤ m(Ckn) ≤ m∗(Ak) + 2 ≤ + m∗(Ak): k=1 k=1 n=1 k=1 k=1 To prove that m∗(A) = m0(A) for any A 2 A we note that for any sequence Cn S1 S1 of sets in A such that A ⊂ n=1 Cn we have A = n=1(Cn \ A) and therefore using the fact that m0 is also countably subadditive for general unions in A and monotone on A 1 1 X X m0(A) ≤ m0(Cn \ A) ≤ m0(Cn) n=1 n=1 proving m0(A) ≤ m∗(A) The reversed inequality is obvious since (A; ;; ;;:::) is a countable cover of A and hence m∗(A) ≤ m0(A). A toy example - pre-measure and construction of outer measure. Let Ω = fa; b; cg, A = f;; fag; fb; cg; Ωg, α; β 2 [0; 1] and define a pre-measure m0 (prove this fact!) by m0(;) = 0; m0(fag) = α; m0(fb; cg) = β; m0(Ω) = α + β CHAPTER 2. THE LEBESGUE INTEGRAL I 13 Then m∗(;) = 0; m∗(fag) = α; m∗(fbg) = β; m∗(fcg) = β and m∗(Ω) = α + β; m∗(fa; bg) = α + β; m∗(fa; cg) = α + β; m∗(fb; cg) = β It is easily seen that m∗jA = m0 and that in general m∗ is not additive, that is m∗ is not a measure on P(Ω). Indeed, if β > 0 , then m∗(fb; cg [ fbg) < m∗(fbg) + m∗(fcg). On the other hand, when β = 0 or β = 1 then m∗ defines a measure on P(Ω). An alternative setting for the construction of outer measures. Since in some situations it may be difficult to find an appropriate algebra (or a pre- measure) we present another setting for constructing outer measures. Let Ω be a nonempty set and E ⊂ P(Ω) be a collection of subsets of Ω such that ;; Ω 2 E. Let m0 : E −! [0; 1] a set function such that m0(;) = 0 (so despite its notation m0 is not necessarily a pre-measure or measure defined on E. As before for any S ⊂ Ω define 1 1 X [ m∗(S) = inff m0(Ek): Ek 2 E;S ⊂ Ekg: (2.12) k=1 k=1 Then m∗ is an outer measure and m∗(E) ≤ m0(E) for all E 2 E (the same proof as above). However, in order to prove m∗(E) = m0(E) we need more restrictive hypotheses on E and m0. Example - Outer measure on Rd. Let E the collection of all countable coverings by (closed) cubes Ck with edges parallel to the axes and let jCkj denote the usual d-dimensional size of a cube. The function 1 X m∗(S) = inf jCkj k=1 where the infimum is taken over all sets in is E an outer measure on Rd. This construction differs from the general approach assuming the sigma-additivity on an algebra for countable unions which are in the algebra but corresponds to the alternative setting. We only have finite additivity but the local compactness of d R (or the compactness of closed cubes) guarantees that m∗(A) = jAj for any closed cube A: Indeed, first note that A covers itself hence m∗(A) ≤ jAj. Then consider any countable covering of A. As before we want to prove that 1 X jAj ≤ jCnj: n=1 For an arbitrary > 0 we choose for each n an open cube On which contains Cn and such that jOnj ≤ (1 + )jCnj. Since A is compact we may select a finite subcovering of A. Consequently, N 1 X X jAj ≤ (1 + ) jCnk j ≤ (1 + ) jCnj: k=1 n=1 The monotonicity and the countable subadditivity are shown as above for an abstract pre-measure. CHAPTER 2. THE LEBESGUE INTEGRAL I 14 Definition - m∗-measurable sets. A set A ⊂ Ω is called m∗-measurable if and only if m∗(E) = m∗(E \ A) + m∗(E n A) for every E ⊂ Ω where E n A = E \ Ac. Note that by the monotonicity of the outer measure we always have the inequality with the ≤ sign. Let Σ∗ denote the family of measurable sets. Sets with outer measure equal to zero are always m∗-measurable. When the outer measure is constructed from a pre-measure defined on an algebra A, then all sets A 2 A are measurable. The notion of m∗- measurable sets filters out sets for which the outer measure m∗ is not additive (for disjoint unions) as we see from our previous toy-example. A toy example - m∗-measurable sets. Recall that Ω = fa; b; cg, A = f;; fag; fb; cg; Ωg, α; β 2 [0; 1] and a pre-measure m0 defined by m0(;) = 0; m0(fag) = α; m0(fb; cg) = β; m0(Ω) = α + β We had seen that when β > 0 , m∗(fb; cg [ fbg) < m∗(fbg) + m∗(fcg). Hence fb; cg is not m∗-measurable. In this case a set is m∗-measurable if and only if it is in the algebra A. Carath´eodory's theorem. With the above notations Σ∗is a sigma algebra and the restriction of m∗ to Σ∗ is a measure µ.
Load more

Recommended publications
  • Measure Theory and Probability Theory
    Measure Theory and Probability Theory Stéphane Dupraz In this chapter, we aim at building a theory of probabilities that extends to any set the theory of probability we have for finite sets (with which you are assumed to be familiar). For a finite set with N elements Ω = {ω1, ..., ωN }, a probability P takes any n positive numbers p1, ..., pN that sum to one, and attributes to any subset S of Ω the number (S) = P p . Extending this definition to infinitely countable sets such as P i/ωi∈S i N poses no difficulty: we can in the same way assign a positive number to each integer n ∈ N and require that P∞ 1 P n=1 pn = 1. We can then define the probability of a subset S ⊆ N as P(S) = n∈S pn. Things get more complicated when we move to uncountable sets such as the real line R. To be sure, it is possible to assign a positive number to each real number. But how to get from these positive numbers to the probability of any subset of R?2 To get a definition of a probability that applies without a hitch to uncountable sets, we give in the strategy we used for finite and countable sets and start from scratch. The definition of a probability we are going to use was borrowed from measure theory by Kolmogorov in 1933, which explains the title of this chapter. What do probabilities have to do with measurement? Simple: assigning a probability to an event is measuring the likeliness of this event.
    [Show full text]
  • Results Real Analysis I and II, MATH 5453-5463, 2006-2007
    Main results Real Analysis I and II, MATH 5453-5463, 2006-2007 Section Homework Introduction. 1.3 Operations with sets. DeMorgan Laws. 1.4 Proposition 1. Existence of the smallest algebra containing C. 2.5 Open and closed sets. 2.6 Continuous functions. Proposition 18. Hw #1. p.16 #9, 11, 17, 18; p.19 #19. 2.7 Borel sets. p.49 #40, 42, 43; p.53 #53*. 3.2 Outer measure. Proposition 1. Outer measure of an interval. Proposition 2. Subadditivity of the outer measure. Proposition 5. Approximation by open sets. 3.3 Measurable sets. Lemma 6. Measurability of sets of outer measure zero. Lemma 7. Measurability of the union. Hw #2. p.55 #1-4; p.58 # 7, 8. Theorem 10. Measurable sets form a sigma-algebra. Lemma 11. Interval is measurable. Theorem 12. Borel sets are measurable. Proposition 13. Sigma additivity of the measure. Proposition 14. Continuity of the measure. Proposition 15. Approximation by open and closed sets. Hw #3. p.64 #9-11, 13, 14. 3.4 A nonmeasurable set. 3.5 Measurable functions. Proposition 18. Equivalent definitions of measurability. Proposition 19. Sums and products of measurable functions. Theorem 20. Infima and suprema of measurable functions. Hw #4. p.70 #18-22. 3.6 Littlewood's three principles. Egoroff's theorem. Lusin's theorem. 4.2 Prop.2. Lebesgue's integral of a simple function and its props. Lebesgue's integral of a bounded measurable function. Proposition 3. Criterion of integrability. Proposition 5. Properties of integrals of bounded functions. Proposition 6. Bounded convergence theorem. 4.3 Lebesgue integral of a nonnegative function and its properties.
    [Show full text]
  • Hausdorff Measure
    Hausdorff Measure Jimmy Briggs and Tim Tyree December 3, 2016 1 1 Introduction In this report, we explore the the measurement of arbitrary subsets of the metric space (X; ρ); a topological space X along with its distance function ρ. We introduce Hausdorff Measure as a natural way of assigning sizes to these sets, especially those of smaller \dimension" than X: After an exploration of the salient properties of Hausdorff Measure, we proceed to a definition of Hausdorff dimension, a separate idea of size that allows us a more robust comparison between rough subsets of X. Many of the theorems in this report will be summarized in a proof sketch or shown by visual example. For a more rigorous treatment of the same material, we redirect the reader to Gerald B. Folland's Real Analysis: Modern techniques and their applications. Chapter 11 of the 1999 edition served as our primary reference. 2 Hausdorff Measure 2.1 Measuring low-dimensional subsets of X The need for Hausdorff Measure arises from the need to know the size of lower-dimensional subsets of a metric space. This idea is not as exotic as it may sound. In a high school Geometry course, we learn formulas for objects of various dimension embedded in R3: In Figure 1 we see the line segment, the circle, and the sphere, each with it's own idea of size. We call these length, area, and volume, respectively. Figure 1: low-dimensional subsets of R3: 2 4 3 2r πr 3 πr Note that while only volume measures something of the same dimension as the host space, R3; length, and area can still be of interest to us, especially 2 in applications.
    [Show full text]
  • Caratheodory's Extension Theorem
    Caratheodory’s extension theorem DBW August 3, 2016 These notes are meant as introductory notes on Caratheodory’s extension theorem. The presentation is not completely my own work; the presentation heavily relies on the pre- sentation of Noel Vaillant on http://www.probability.net/WEBcaratheodory.pdf. To make the line of arguments as clear as possible, the starting point is the notion of a ring on a topological space and not the notion of a semi-ring. 1 Elementary definitions and properties We fix a topological space Ω. The power set of Ω is denoted P(Ω) and consists of all subsets of Ω. Definition 1. A ring on on Ω is a subset R of P(Ω), such that (i) ∅ ∈ R (ii) A, B ∈ R ⇒ A ∪ B ∈ R (iii) A, B ∈ R ⇒ A \ B ∈ R Definition 2. A σ-algebra on Ω is a subset Σ of P(Ω) such that (i) ∅ ∈ Σ (ii) (An)n∈N ∈ Σ ⇒ ∪n An ∈ Σ (iii) A ∈ Σ ⇒ Ac ∈ Σ Since A∩B = A\(A\B) it follows that any ring on Ω is closed under finite intersections; c c hence any ring is also a semi-ring. Since ∩nAn = (∪nA ) it follows that any σ-algebra is closed under arbitrary intersections. And from A \ B = A ∩ Bc we deduce that any σ-algebra is also a ring. If (Ri)i∈I is a set of rings on Ω then it is clear that ∩I Ri is also a ring on Ω. Let S be any subset of P(Ω), then we call the intersection of all rings on Ω containing S the ring generated by S.
    [Show full text]
  • Construction of Geometric Outer-Measures and Dimension Theory
    Construction of Geometric Outer-Measures and Dimension Theory by David Worth B.S., Mathematics, University of New Mexico, 2003 THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science Mathematics The University of New Mexico Albuquerque, New Mexico December, 2006 c 2008, David Worth iii DEDICATION To my lovely wife Meghan, to whom I am eternally grateful for her support and love. Without her I would never have followed my education or my bliss. iv ACKNOWLEDGMENTS I would like to thank my advisor, Dr. Terry Loring, for his years of encouragement and aid in pursuing mathematics. I would also like to thank Dr. Cristina Pereyra for her unfailing encouragement and her aid in completing this daunting task. I would like to thank Dr. Wojciech Kucharz for his guidance and encouragement for the entirety of my adult mathematical career. Moreover I would like to thank Dr. Jens Lorenz, Dr. Vladimir I Koltchinskii, Dr. James Ellison, and Dr. Alexandru Buium for their years of inspirational teaching and their influence in my life. v Construction of Geometric Outer-Measures and Dimension Theory by David Worth ABSTRACT OF THESIS Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science Mathematics The University of New Mexico Albuquerque, New Mexico December, 2006 Construction of Geometric Outer-Measures and Dimension Theory by David Worth B.S., Mathematics, University of New Mexico, 2003 M.S., Mathematics, University of New Mexico, 2008 Abstract Geometric Measure Theory is the rigorous mathematical study of the field commonly known as Fractal Geometry. In this work we survey means of constructing families of measures, via the so-called \Carath´eodory construction", which isolate certain small- scale features of complicated sets in a metric space.
    [Show full text]
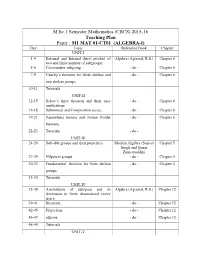
  • M.Sc. I Semester Mathematics (CBCS) 2015-16 Teaching Plan
    M.Sc. I Semester Mathematics (CBCS) 2015-16 Teaching Plan Paper : M1 MAT 01-CT01 (ALGEBRA-I) Day Topic Reference Book Chapter UNIT-I 1-4 External and Internal direct product of Algebra (Agrawal, R.S.) Chapter 6 two and finite number of subgroups; 5-6 Commutator subgroup - do - Chapter 6 7-9 Cauchy’s theorem for finite abelian and - do - Chapter 6 non abelian groups. 10-11 Tutorials UNIT-II 12-15 Sylow’s three theorem and their easy - do - Chapter 6 applications 16-18 Subnormal and Composition series, - do - Chapter 6 19-21 Zassenhaus lemma and Jordan Holder - do - Chapter 6 theorem. 22-23 Tutorials - do - UNIT-III 24-26 Solvable groups and their properties Modern Algebra (Surjeet Chapter 5 Singh and Quazi Zameeruddin) 27-29 Nilpotent groups - do - Chapter 5 30-32 Fundamental theorem for finite abelian - do - Chapter 4 groups. 33-34 Tutorials UNIT-IV 35-38 Annihilators of subspace and its Algebra (Agrawal, R.S.) Chapter 12 dimension in finite dimensional vector space 39-41 Invariant, - do - Chapter 12 42-45 Projection, - do - Chapter 12 46-47 adjoins. - do - Chapter 12 48-49 Tutorials UNIT-V 50-54 Singular and nonsingular linear Algebra (Agrawal, R.S.) Chapter 12 transformation 55-58 quadratic forms and Diagonalization. - do - Chapter12 59-60 Tutorials - do - 61-65 Students Interaction & Difficulty solving - - M.Sc. I Semester Mathematics (CBCS) 2015-16 Teaching Plan Paper : M1 MAT 02-CT02 (REAL ANALYSIS) Day Topic Reference Book Chapter UNIT-I 1-2 Length of an interval, outer measure of a Theory and Problems of Chapter 2 subset of R, Labesgue outer measure of a Real Variables: Murray subset of R R.
    [Show full text]
  • Section 17.5. the Carathéodry-Hahn Theorem: the Extension of A
    17.5. The Carath´eodory-Hahn Theorem 1 Section 17.5. The Carath´eodry-Hahn Theorem: The Extension of a Premeasure to a Measure Note. We have µ defined on S and use µ to define µ∗ on X. We then restrict µ∗ to a subset of X on which µ∗ is a measure (denoted µ). Unlike with Lebesgue measure where the elements of S are measurable sets themselves (and S is the set of open intervals), we may not have µ defined on S. In this section, we look for conditions on µ : S → [0, ∞] which imply the measurability of the elements of S. Under these conditions, µ is then an extension of µ from S to M (the σ-algebra of measurable sets). ∞ Definition. A set function µ : S → [0, ∞] is finitely additive if whenever {Ek}k=1 ∞ is a finite disjoint collection of sets in S and ∪k=1Ek ∈ S, we have n n µ · Ek = µ(Ek). k=1 ! k=1 [ X Note. We have previously defined finitely monotone for set functions and Propo- sition 17.6 gives finite additivity for an outer measure on M, but this is the first time we have discussed a finitely additive set function. Proposition 17.11. Let S be a collection of subsets of X and µ : S → [0, ∞] a set function. In order that the Carath´eodory measure µ induced by µ be an extension of µ (that is, µ = µ on S) it is necessary that µ be both finitely additive and countably monotone and, if ∅ ∈ S, then µ(∅) = 0.
    [Show full text]
  • Abelian Group, 521, 526 Absolute Value, 190 Accumulation, Point Of
    Index Abelian group, 521, 526 A-set. SeeAnalytic set Absolutevalue, 190 Asymptoticallyequal. 479 Accumulation, point of, 196 Atlas , 231; of holomorphically related Adjoint differentialform, 157, 167 charts, 245 Adjoint operator, 403 Atomic theory, 415 Adjoint space, 397 Automorphism group, 510, 511 Algebra, 524; Boolean, 91, 92; Axiomatic method, in geometry, 507-508 fundamentaltheorem of, 195-196; homo logical, 519-520; normed, 516 BAIREclasses, 460; first, 460, 462, 463; Almost all, 479 of functions, 448 Almost continuous, 460 BAIREcondition, 464 Almost equal, 479 BAIREfunction, 464, 473; non-, 474 Almost everywhere, 70 BAIREspace, 464 Almost linear equation, 321, 323 BAIREsystem, of functions, 459, 460 Alternating differentialform, 185; BAIREtheorem, 448, 460, 462 differentialoperations for, 159-165; BANACH, S., 516 theory of, vi, 143 BANACHfixed point theorem, 423 Alternative theorem, 296, 413 BANACHspace, 338, 340, 393, 399, 432, Analysis, v, 1; axiomaticmethod in, 435,437, 516; adjoint, 400; 512-518; complex, vi ; functional, conjugate, 400; dual, 400; theory of, vi 391; harmonic, 518; and number BANACHtheorem, 446, 447 theory, 500-501 Band spectra, 418 Analytic function, definedby function BAYES theorem, 109 element, 242 BELTRAMIdifferential equation, 325 Analytic numbertheory, 480 BERNOULLI, DANIEL, 23 Analytic operation, 468 BERNOULLI, JACOB, 89, 360 Analytic set, 448, 458, 465, 468, 469; BERNOULLI, JOHANN, 23 linear, 466 BERNOULLIdistribution, 96 Angle-preservingtransformation, 194 BERNOULLIlaw, of large numbers, 116 a-points,
    [Show full text]
  • 2.5 Outer Measure and Measurable Sets. Note the Results of This Section Concern Any Given Outer Measure Λ
    2.5 Outer Measure and Measurable sets. Note The results of this section concern any given outer measure ¸. If an outer measure ¸ on a set X were a measure then it would be additive. In particular, given any two sets A; B ⊆ X we have that A \ B and A \ Bc are disjoint with (A \ B) [ (A \ Bc) = A and so we would have ¸(A) = ¸(A \ B) + ¸(A \ Bc): We will see later that this does not necessarily hold for all A and B but it does lead to the following definition. Definition Let ¸ be an outer measure on a set X. Then E ⊆ X is said to be measurable with respect to ¸ (or ¸-measurable) if ¸(A) = ¸(A \ E) + ¸(A \ Ec) for all A ⊆ X. (7) (This can be read as saying that we take each and every possible “test set”, A, look at the measures of the parts of A that fall within and without E, and check whether these measures add up to that of A.) Since ¸ is subadditive we have ¸(A) · ¸(A\E)+¸(A\Ec) so, in checking measurability, we need only verify that ¸(A) ¸ ¸(A \ E) + ¸(A \ Ec) for all A ⊆ X. (8) Let M = M(¸) denote the collection of ¸-measurable sets. Theorem 2.6 M is a field. Proof Trivially Á and X are in M. Take any E1;E2 2 M and any test set A ⊆ X. Then c ¸(A) = ¸(A \ E1) + ¸(A \ E1): c Now apply the definition of measurability for E2 with the test set A \ E1 to get c c c c ¸(A \ E1) = ¸((A \ E1) \ E2) + ¸((A \ E1) \ E2) c c = ¸(A \ E1 \ E2) + ¸(A \ (E1 [ E2) ): Combining c c ¸(A) = ¸(A \ E1) + ¸(A \ E1 \ E2) + ¸(A \ (E1 [ E2) ): (9) 1 We hope to use the subadditivity of ¸ on the first two term on the right hand side of (9).
    [Show full text]
  • PATHOLOGICAL 1. Introduction
    PATHOLOGICAL APPLICATIONS OF LEBESGUE MEASURE TO THE CANTOR SET AND NON-INTEGRABLE DERIVATIVES PRICE HARDMAN WHITMAN COLLEGE 1. Introduction Pathological is an oft used word in the mathematical community, and in that context it has quite a different meaning than in everyday usage. In mathematics, something is said to be \pathological" if it is particularly poorly behaved or counterintuitive. However, this is not to say that mathe- maticians use this term in an entirely derisive manner. Counterintuitive and unexpected results often challenge common conventions and invite a reevalu- ation of previously accepted methods and theories. In this way, pathological examples can be seen as impetuses for mathematical progress. As a result, pathological examples crop up quite often in the history of mathematics, and we can usually learn a great deal about the history of a given field by studying notable pathological examples in that field. In addition to allowing us to weave historical narrative into an otherwise noncontextualized math- mematical discussion, these examples shed light on the boundaries of the subfield of mathematics in which we find them. It is the intention then of this piece to investigate the basic concepts, ap- plications, and historical development of measure theory through the use of pathological examples. We will develop some basic tools of Lebesgue mea- sure on the real line and use them to investigate some historically significant (and fascinating) examples. One such example is a function whose deriva- tive is bounded yet not Riemann integrable, seemingly in violation of the Fundamental Theorem of Calculus. In fact, this example played a large part in the development of the Lebesgue integral in the early years of the 20th century.
    [Show full text]
  • Lecture Notes for Data and Uncertainty (First Part)
    Lecture Notes for Data and Uncertainty (first part) Jochen Bröcker December 29, 2020 1 Introduction Sections 1 to 10 will cover probability theory, integration, and a bit of statis- tics (roughly in that order). The second part (Sect. 11-13) –not part of these notes– will explain an important technique in statistics called Monte Carlo simulations. This introduction will motivate probability theory and statistics a little bit, and in particular why we need concepts from measure theory and integration, which is often perceived as abstract and complicated. Probability It is not easy to explain what probability theory is about without sounding tautological. One might say that it allows to quantify uncertainty or chance, but then what do we mean by “uncertainty” or “chance”? De Moivre’s seminal textbook “The Doctrine of Chances” [dM67] is widely considered as the first textbook on probability theory, and the theory has undergone enormous developments since then. In particular, there is an ax- iomatic framework which has been universally adopted and which we will discuss in this course. But even though De Moivre’s book was first published in 1718, there is still some debate as to the interpretation of probability theory, or in other words, to what this nice axiomatic framework actually pertains. Different interpretations of probability have been put forward, but somewhat fortunately to the student, the differences matter little as far as the mathematics is concerned. Nonetheless, we will briefly mention the most prominent interpretations of probability
    [Show full text]
  • Measure Theory
    Appendix A Measure theory In this appendix we collect some important notions from measure theory. The goal is not to present a self-contained presentation, but rather to establish the basic definitions and theorems from the theory for reference in the main text. As such, the presentation omits certain existence theorems and many of the proofs of other theorems (although references are given). The focus is strongly on finite (e.g. probability-) measures, in places at the expense of generality. Some background in elementary set-theory and analysis is required. As a comprehensive reference, we note Kingman and Taylor (1966) [52], alternatives being Dudley (1989) [29] and Billingsley (1986) [15]. A.1 Sets and sigma-algebras Rough setup: set operations, monotony of sequences of subsets, set-limits, sigma-algebra’s, measurable spaces, set-functions, product spaces. Definition A.1.1. A measurable space (Ω, F ) consists of a set Ω and a σ-algebra F of subsets of Ω. A.2 Measures Rough setup: set-functions, (signed) measures, probability measures, sigma-additivity, sigma- finiteness Theorem A.2.1. Let (Ω, F ) be a measurable space with measure µ : F [0, ]. Then, → ∞ (i) for any monotone decreasing sequence (Fn)n 1 in F such that µ(Fn) < for some n, ≥ ∞ ∞ lim µ(Fn)=µ Fn , (A.1) n →∞ n=1 91 92 Measure theory (ii) for any monotone increasing sequence (Gn)n 1 in F , ≥ ∞ lim µ(Gn)=µ Gn , (A.2) n →∞ n=1 Theorem A.2.1) is sometimes referred to as the continuity theorem for measures, because if we view F as the monotone limit lim F , (A.1) can be read as lim µ(F )=µ(lim F ), ∩n n n n n n n expressing continuity from below.
    [Show full text]