DOCSLIB.ORG

Overall Heat Transfer Coefficient- LMTD and NTU Methods- Fouling in Heat Exchangers- Heat Exchangers with Phase Change

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Overall Heat Transfer Coefficient- LMTD and NTU Methods- Fouling in Heat Exchangers- Heat Exchangers with Phase Change MALLA REDDY COLLEGE OF ENGINEERING & TECHNOLOGY (Autonomous Institution – UGC, Govt. of India) Sponsored by CMR Educational Society (Affiliated to JNTU, Hyderabad, Approved by AICTE - Accredited by NBA & NAAC – A Grade - ISO 9001:2015 Certified) Maisammaguda, Dhulapally (Post Via. Kompally), Secunderabad – 500100, Telangana State, India. DEPARTMENT OF MECHANICAL ENGINEERING HEAT TRANSFER DIGITAL NOTES for B.TECH - III YEAR – II SEMESTER (2017-18) MALLA REDDY COLLEGE OF ENGINEERING & TECHNOLOGY L T/P/D C III Year B. Tech, ME-II Sem 5 1 4 (R15A0323) HEAT TRANSFER *Note: Heat and Mass Transfer data books are permitted Objectives: The objective of this subject is to provide knowledge about Heat transfer through conduction, convection and radiation. Student able to learn different modes of Heat Transfer. Student able to learn about the dimensional analysis . UNIT-I Introduction: Basic modes of heat transfer- Rate equations- Generalized heat conduction equation in Cartesian, Cylindrical and Spherical coordinate systems. Steady state heat conduction solution for plain and composite slabs, cylinders and spheres- Critical thickness of insulation- Heat conduction through fins of uniform and variable cross section- Fin effectiveness and efficiency. Unsteady state Heat Transfer conduction- Transient heat conduction- Lumped system analysis, and use of Heisler charts. UNIT-II Convection: Continuity, momentum and energy equations- Dimensional analysis- Boundary layer theory concepts- Free, and Forced convection- Approximate solution of the boundary layer equations- Laminar and turbulent heat transfer correlation- Momentum equation and velocity profiles in turbulent boundary layers- Application of dimensional analysis to free and forced convection problems- Empirical correlation. UNIT-III Radiation: Black body radiation- radiation field, Kirchhoff’s laws- shape factor- Stefan Boltzman equation- Heat radiation through absorbing media- Radiant heat exchange, parallel and perpendicular surfaces- Radiation shields. UNIT-IV Heat Exchangers: Types of heat exchangers- Parallel flow- Counter flow- Cross flow heat exchangers- Overall heat transfer coefficient- LMTD and NTU methods- Fouling in heat exchangers- Heat exchangers with phase change. Boiling and Condensation: Different regimes of boiling- Nucleate, Transition and Film boiling. Condensation: Laminar film condensation- Nusselt's theory- Condensation on vertical flat plate and horizontal tubes- Drop wise condensation. UNIT-V Mass Transfer: Conservation laws and constitutive equations- Isothermal equimass, Equimolal diffusion- Fick's law of diffusion- diffusion of gases, Liquids- Mass transfer coefficient. TEXT BOOKS: 1. Heat Transfer, by J.P.Holman, Int.Student edition, McGraw Hill Book Company. 2. Fundamentals of Heat and Mass Transfer- Sachdeva. 3. Heat transfer by Arora and Domakundwar, Dhanpat Rai & sons, New Delhi.. REFERENCE BOOKS: 1. Heat Transfer by Sukhatme. 2. Heat and Mass Transfer by R.K.Rajput, Laxmi Publications, New Delhi. 3. Heat transfer by Yunus A Cengel. OUTCOMES: Knowledge and understanding how heat and energy is transferred between the elements of a system for different configurations. Solve problems involving one or more modes of heat transfer. Student gets the exposure of different modes of Heat Transfer. UNIT-I Modes of Heat Transfer Heat Transfer by Conduction Fourier's Law of Heat Conduction dt Q =- Ka dx dt The temperature gradient is always negative along positive x direction and, dx therefore, the value as Q becomes + ve. Essential Features of Fourier’s law: 1. It is applicable to all matter (may be solid, liquid or gas). 2. It is a vector expression indicating that heat flow rate is in the direction of decreasing temperature and is normal to an isotherm. 3. It is based on experimental evidence and cannot be derived from first principle. Thermal Conductivity of Materials Sl. NO. Materials Thermal conductivity, (k) 1 Silver 10 W/mk 2 Copper 85 W/mk 3 Aluminium 25 W/mk 4 Steel 40 W/mk 5 Saw dust 0.07 W/mk 6 Glass wool 0.03 W/mk 7 Freon 0.0083 W/mk A. Pure metals, (k) = 10 to 400 W/mk Solid: B. Alloys, (k) = 10 to 120 W/mk C. Insulator, (k) = 0.023 to 2.9 W/mk Liquid: k = 0.2 to 0.5 W/mk Gas: k = 0.006 to 0.5 W/mk Thermal conductivity and temperature: k = k 0 (1+ βt ) Al ,U ( i ) Metals, k if t except. i.e. β ,−ve ( ii ) Liquid k if t except. H O 2 ( iii )Gas k if t ( iv ) Non -metal and i.e. ,+ ve β insulating material k if t various parameters on the thermal conductivity of solids. The following are the effects of various parameters on the thermal conductivity of solids. 1. Chemical composition: Pure metals have very high thermal conductivity. Impurities or alloying elements reduce the thermal conductivity considerably [Thermal conductivity of pure copper is 385 W/mºC, and that for pure nickel is 93 W/mºC. But monel metal (an alloy of 30% Ni and 70% Cu) has k of 24 W/mºC. Again for copper containing traces of Arsenic the value of k is reduced to 142 W/mºC]. 2. Mechanical forming: Forging, drawing and bending or heat treatment of metals causes considerable variation in thermal conductivity. For example, the thermal conductivity of hardened steel is lower than that of annealed state. 3. Temperature rise: The value of k for most metals decreases with temperature rise since at elevated temperatures the thermal vibrations of the lattice become higher that retard the motion of free electrons. 4. Non-metallic solids: Non-metallic solids have k much lower than that for metals. For many of the building materials (concrete, stone, brick, glass wool, cork etc.) the thermal conductivity may vary from sample to sample due Fire brick to variations in structure, composition, density and porosity. 5. Presence of air: The thermal conductivity is reduced due to the presence of air filled pores or cavities. 6. Dampness: Thermal conductivity of a damp material is considerably higher than that of dry material. 7. Density: Thermal conductivity of insulating powder, asbestos etc. increases with density Growth. Thermal conductivity of snow is also proportional to its density. Thermal Conductivity of Liquids V s k = 3 2 R Where = Boltzmann constant per molecule A v (Don’t confused with Stefen Boltzmann Constant) Vs = Sonic velocity of molecule = Distance between two adjacent molecule. R = Universal gas constant Av = Avogadro’s number Thermal conductivity of gas 1 k = nv f s 6 Where n = Number of molecule/unit volume v s = Arithmetic mean velocity f = Number of DOF = Molecular mean free path For liquid thermal conductivity lies in the range of 0.08 to 0.6 W/m-k For gases thermal conductivity lies in the range of 0.005 to 0.05 W/m-k The conductivity of the fluid related to dynamic viscosity () 4.5 k = 1 + 2n Cv ; l where, n = number of atoms in a molecule Sequence of thermal conductivity Pure metals > alloy > non-metallic crystal and amorphous > liquid > gases Wiedemann and Franz Law (based on experimental results) The ratio of the thermal and electrical conductivities is the same for all metals at the same temperature; and that the ratio is directly proportional to the absolute temperature of the metal. ’’ k k Where T or C α = T k = Thermal conductivity at T(K) υ υ υ = Electrical conductivity at T(K) − C = Lorenz number = 2.45 × 10 8 wΩ / k2 This law conveys that: the metals which are good conductors of electricity are also good conductors of heat. Except mica. Thermal Resistance: (Rth) Ohm’s Law: Flow of Electricity Voltage Drop = Current flow × Resistance Thermal Analogy to Ohm’s Law: T = qRth Temperature Drop = Heat Flow × Resistance A. Conduction Thermal Resistance: L (i) Slab ( R ) = th k A n ( r / r ) 2 1 (ii) Hollow cylinder ( R ) = th 2 kL π r r (iii) Hollow sphere ( R ) = 2 − 1 th 4 kr r π 1 2 1 B. Convective Thermal Resistance: ( R ) = th hA 1 C. Radiation Thermal Resistance: R = ( th ) 2 2 T + T2 )(T1 + T2 ) F A( 1 1D Heat Conduction through a Plane Wall (Thermal resistance) 1 L 1 R = t + + ∑ h1 A kA h2 A 1D Conduction (Radial conduction in a composite cylinder) 1D Conduction in Sphere Inside Solid: 1 d dT 2 kr 2 = 0 r dr dr 1 ( r1 / r) − T − T (r ) Ts , Ts ,1 s,2 = 1 − { } r1 / r2 1 − ( ) 4π k T − T qr = − kA dT = ( ( s ,1 s,)2 ) dr 1 / r1 − 1 / r2 = 1 / r1 1 / r2 R − t , cond 4 k π Isotropic & Anisotropic material If the directional characteristics of a material are equal /same, it is called an ‘Isotropic material’ and if unequal/different ‘Anisotropic material’. Example: Which of the following is anisotropic, i.e. exhibits change in thermal conductivity due to directional preferences? (a) Wood (b) Glass wool (c) Concrete (d) Masonry brick Answer. (a) ( ( ) Thermalconductivity k) Thermal diffusivity α = Thermalcapacity ( ρ c) 2 i. e . α = k unit m s c ρ The larger the value of α, the faster will be the heat diffuse through the material and its temperature will change with time. – Thermal diffusivity is an important characteristic quantity for unsteady condition situation. One Dimensional Steady State Conduction General Heat Conduction Equation in Cartesian Coordinates Recognize that heat transfer involves an energy transfer across a system boundary. A logical place to begin studying such process is from Conservation of Energy (1st Law of – Thermodynamics) for a closed system: dE i i Q W out = in − dt system The sign convention on work is such that negative work out is positive work in: i i dE = Q in + W out dt system The work in term could describe an electric current flow across the system boundary and through a resistance inside the system. Alternatively it could describe a shaft turning across the system boundary and overcoming friction within the system.
Load more

Recommended publications
  • The Body in Question: the Income Tax and Human Body Materials
    ZELENAK_FORMATTED_PREPROOF_PERMA (DO NOT DELETE) 3/14/2017 2:18 PM THE BODY IN QUESTION: THE INCOME TAX AND HUMAN BODY MATERIALS ∗ LAWRENCE ZELENAK I INTRODUCTION The federal income tax treatment of transactions in human body materials— such as eggs, sperm, blood, milk, hair, and kidneys—is a mess. Nothing is firmly settled. Consider, for example, the recent first-impression case of Perez v. Commissioner,1 in which the Tax Court concluded that a paid “donor” of ova had received fully taxable compensation-for-services income (rejecting the taxpayer’s claim that the payments qualified under the statutory exclusion from gross income of “damages . on account of personal physical injuries”2). By contrast, academic commentators writing before Perez had thought it fairly obvious that a paid egg donor was the seller of an asset,3 thus giving rise to at least the possibility of taxation at the favorable rates applicable to long-term capital gain. Similar confusion reigns in the case of taxpayers who donate their blood to charity. There is support both for the proposition that a blood donor performs a service for the charity4 (and so is subject to the rule that contributions of services are not deductible5), and also for the proposition that a blood donation is a contribution of property (the value of which would be deductible but for the happenstance that blood cells do not live long enough to satisfy the holding period for long-term capital gain).6 Although the same no-deduction result is Copyright © 2017 by Lawrence Zelenak. This article is also available online at http://lcp.law.duke.edu/.
    [Show full text]
  • 8123 Songs, 21 Days, 63.83 GB
    Page 1 of 247 Music 8123 songs, 21 days, 63.83 GB Name Artist The A Team Ed Sheeran A-List (Radio Edit) XMIXR Sisqo feat. Waka Flocka Flame A.D.I.D.A.S. (Clean Edit) Killer Mike ft Big Boi Aaroma (Bonus Version) Pru About A Girl The Academy Is... About The Money (Radio Edit) XMIXR T.I. feat. Young Thug About The Money (Remix) (Radio Edit) XMIXR T.I. feat. Young Thug, Lil Wayne & Jeezy About Us [Pop Edit] Brooke Hogan ft. Paul Wall Absolute Zero (Radio Edit) XMIXR Stone Sour Absolutely (Story Of A Girl) Ninedays Absolution Calling (Radio Edit) XMIXR Incubus Acapella Karmin Acapella Kelis Acapella (Radio Edit) XMIXR Karmin Accidentally in Love Counting Crows According To You (Top 40 Edit) Orianthi Act Right (Promo Only Clean Edit) Yo Gotti Feat. Young Jeezy & YG Act Right (Radio Edit) XMIXR Yo Gotti ft Jeezy & YG Actin Crazy (Radio Edit) XMIXR Action Bronson Actin' Up (Clean) Wale & Meek Mill f./French Montana Actin' Up (Radio Edit) XMIXR Wale & Meek Mill ft French Montana Action Man Hafdís Huld Addicted Ace Young Addicted Enrique Iglsias Addicted Saving abel Addicted Simple Plan Addicted To Bass Puretone Addicted To Pain (Radio Edit) XMIXR Alter Bridge Addicted To You (Radio Edit) XMIXR Avicii Addiction Ryan Leslie Feat. Cassie & Fabolous Music Page 2 of 247 Name Artist Addresses (Radio Edit) XMIXR T.I. Adore You (Radio Edit) XMIXR Miley Cyrus Adorn Miguel Adorn Miguel Adorn (Radio Edit) XMIXR Miguel Adorn (Remix) Miguel f./Wiz Khalifa Adorn (Remix) (Radio Edit) XMIXR Miguel ft Wiz Khalifa Adrenaline (Radio Edit) XMIXR Shinedown Adrienne Calling, The Adult Swim (Radio Edit) XMIXR DJ Spinking feat.
    [Show full text]
  • Axon February 2019 Release Notes
    Axon February 2019 Release Notes Document Revision: A Evidence.com Version 2019.2 Axon February 2019 Release Notes Apple, iOS, and Safari are trademarks of Apple, Inc. registered in the US and other countries. Firefox is a trademark of The Mozilla Foundation registered in the US and other countries. Google, Google Play, Android, and Chrome are trademarks of Google, Inc. Microsoft, Windows, Internet Explorer, and Excel are trademarks of Microsoft Corporation registered in the US and other countries. Javascript is a trademark of Oracle America, Inc. registered in the US and other countries. , Axon, Axon Body, Axon Body 2, Axon Capture, Axon Citizen, Axon Dock, Axon Fleet, Axon Fleet 2, Axon Flex, Axon Flex 2, Axon Interview, Axon View, Axon View XL, Evidence.com (Axon Evidence), Evidence.com Lite, Evidence Sync, and TASER are trademarks of Axon Enterprise, Inc., some of which are registered in the US and other countries. For more information, visit www.axon.com/legal. All rights reserved. ©2019 Axon Enterprise, Inc. Axon Enterprise, Inc. Page 2 of 24 Axon February 2019 Release Notes Table of Contents Overview ...................................................................................................................................................... 5 Important Information for Evidence Sync users with Axon Body 2...................................................... 5 Axon Evidence.com February Release Updates ...................................................................................... 5 Evidence Groups .......................................................................................................................................
    [Show full text]
  • United States District Court Eastern District Of
    Case 2:13-cv-05463-KDE-SS Document 1 Filed 08/16/13 Page 1 of 118 UNITED STATES DISTRICT COURT EASTERN DISTRICT OF LOUISIANA PAUL BATISTE D/B/A * CIVIL ACTION NO. ARTANG PUBLISHING LLC * * SECTION: “ ” Plaintiff, * * JUDGE VERSUS * * MAGISTRATE FAHEEM RASHEED NAJM, P/K/A T-PAIN, KHALED * BIN ABDUL KHALED, P/K/A DJ KHALED, WILLIAM * ROBERTS II, P/K/A RICK ROSS, ANTOINE * MCCOLISTER P/K/A ACE HOOD, 4 BLUNTS LIT AT * ONCE PUBLISHING, ATLANTIC RECORDING * CORPORATION, BYEFALL MUSIC LLC, BYEFALL * PRODUCTIONS, INC., CAPITOL RECORDS LLC, * CASH MONEY RECORDS, INC., EMI APRIL MUSIC, * INC., EMI BLACKWOOD MUSIC, INC., * FIRST-N-GOLD PUBLISHING, INC., FUELED BY * RAMEN, LLC, NAPPY BOY, LLC, NAPPY BOY * ENTERPRISES, LLC, NAPPY BOY PRODUCTIONS, * LLC, NAPPY BOY PUBLISHING, LLC, NASTY BEAT * MAKERS PRODUCTIONS, INC., PHASE ONE * NETWORK, INC., PITBULL’S LEGACY * PUBLISHING, RCA RECORDS, RCA/JIVE LABEL * GROUP, SONGS OF UNIVERSAL, INC., SONY * MUSIC ENTERTAINMENT DIGITAL LLC, * SONY/ATV MUSIC PUBLISHING, LLC, SONY/ATV * SONGS, LLC, SONY/ATV TUNES, LLC, THE ISLAND * DEF JAM MUSIC GROUP, TRAC-N-FIELD * ENTERTAINMENT, LLC, UMG RECORDINGS, INC., * UNIVERSAL MUSIC – MGB SONGS, UNIVERSAL * MUSIC – Z TUNES LLC, UNIVERSAL MUSIC * CORPORATION, UNIVERSAL MUSIC PUBLISHING, * INC., UNIVERSAL-POLYGRAM INTERNATIONAL * PUBLISHING, INC., WARNER-TAMERLANE * PUBLISHING CORP., WB MUSIC CORP., and * ZOMBA RECORDING LLC * * Defendants. * ****************************************************************************** Case 2:13-cv-05463-KDE-SS Document 1 Filed 08/16/13 Page 2 of 118 COMPLAINT Plaintiff Paul Batiste, doing business as Artang Publishing, LLC, by and through his attorneys Koeppel Traylor LLC, alleges and complains as follows: INTRODUCTION 1. This is an action for copyright infringement.
    [Show full text]
  • Standard Operating Procedure Whitefish Bay Police Department
    STANDARD OPERATING PROCEDURE WHITEFISH BAY POLICE DEPARTMENT SUBJECT: BODY WORN CAMERAS REVISED: 02/11/2020 ISSUED: 01/29/2019 SCOPE: All Sworn Personnel EFFECTIVE: 01/29/2019 DISTRIBUTION: Standard Operating Procedure Manual × RESCINDS 5/22/18 SOP AMENDS REFERENCE: WILEAG 5TH EDITION STANDARDS: PURPOSE: The purpose of this policy is to establish guidelines for the use, management, storage and retrieval of recordings from the department’s body worn camera (BWC) system. BWC’s will be used to support the mission of the department and assist department members in the performance of their duties by providing an accurate and unbiased recording of interactions between police members and the public. Each BWC system will be used to document various events that occur during the duty shift of the assigned member. Upon completion of the assigned member’s shift, all captured data will be preserved in a secure recording storage location. Once captured, these recordings are protected with multiple layers of encryption and cannot be altered. BWC technology facilitates the department’s objectives to collect evidence for prosecutions, ensures both officer and citizen accountability, facilitates administrative inspection functions, and provides a valuable training aid by allowing for the evaluation of officer and citizen behavior. This Standard Operating Procedure consists of the following numbered sections: I. DEFINITIONS II. DIRECTIVES III. OPERATIONAL GUIDELINES 1 I. DEFINITIONS A. AXON MOBILE SMARTPHONE APPLICATION A smartphone application (app) that allows for a Bluetooth connection from the camera to a supported smartphone device. The app will allow a member to view live or recorded video stored on the camera.
    [Show full text]
  • Geographic Perspectives on Contemporary / Smooth Jazz
    GEOGRAPHIC PERSPECTIVES ON CONTEMPORARY / SMOOTH JAZZ By WILLIAM ROBERT FLYNN Bachelor of Music in Classical Guitar Performance California State University, Fullerton Fullerton, California 2000 Master of Applied Geography Texas State University San Marcos, Texas 2001 Submitted to the Faculty of the Graduate College of the Oklahoma State University in partial fulfillment of the requirements for the Degree of DOCTOR OF PHILOSOPHY December, 2014 GEOGRAPHIC PERSPECTIVES ON CONTEMPORARY / SMOOTH JAZZ Dissertation Approved: Dr. G. Allen Finchum Dissertation Adviser Dr. Brad A. Bays Dr. Jonathan C. Comer Dr. Thomas Lanners Outside Committee Member ii ACKNOWLEDGEMENTS Completing this dissertation and my doctoral program at Oklahoma State University would not have been possible without the support of many people over the past ten years. I would like to start with my advisor and chair, Dr. Allen Finchum, who not only happens to share my interest in smooth jazz, but has always been there for me. One could not ask for a better mentor, as he was always so giving of his time, whether we were discussing my research, talking about my experiences as a graduate instructor, or him just taking an interest in my personal life. I feel blessed to have been able to work with such a special graduate committee, comprised of Dr. Jon Comer, Dr. Brad Bays, and Dr. Tom Lanners. Dr. Comer sparked my passion for quantitative methods and spatial analysis, and Dr. Bays taught my very first course at OSU, a wonderful and stimulating seminar in historical geography. With Dr. Lanners, I could not have asked for a better fit for my outside committee member, and I feel privileged to have been able to work with a musician of his caliber.
    [Show full text]
  • Songs by Artist
    Songs by Artist Karaoke Collection Title Title Title +44 18 Visions 3 Dog Night When Your Heart Stops Beating Victim 1 1 Block Radius 1910 Fruitgum Co An Old Fashioned Love Song You Got Me Simon Says Black & White 1 Fine Day 1927 Celebrate For The 1st Time Compulsory Hero Easy To Be Hard 1 Flew South If I Could Elis Comin My Kind Of Beautiful Thats When I Think Of You Joy To The World 1 Night Only 1st Class Liar Just For Tonight Beach Baby Mama Told Me Not To Come 1 Republic 2 Evisa Never Been To Spain Mercy Oh La La La Old Fashioned Love Song Say (All I Need) 2 Live Crew Out In The Country Stop & Stare Do Wah Diddy Diddy Pieces Of April 1 True Voice 2 Pac Shambala After Your Gone California Love Sure As Im Sitting Here Sacred Trust Changes The Family Of Man 1 Way Dear Mama The Show Must Go On Cutie Pie How Do You Want It 3 Doors Down 1 Way Ride So Many Tears Away From The Sun Painted Perfect Thugz Mansion Be Like That 10 000 Maniacs Until The End Of Time Behind Those Eyes Because The Night 2 Pac Ft Eminem Citizen Soldier Candy Everybody Wants 1 Day At A Time Duck & Run Like The Weather 2 Pac Ft Eric Will Here By Me More Than This Do For Love Here Without You These Are Days 2 Pac Ft Notorious Big Its Not My Time Trouble Me Runnin Kryptonite 10 Cc 2 Pistols Ft Ray J Let Me Be Myself Donna You Know Me Let Me Go Dreadlock Holiday 2 Pistols Ft T Pain & Tay Dizm Live For Today Good Morning Judge She Got It Loser Im Mandy 2 Play Ft Thomes Jules & Jucxi So I Need You Im Not In Love Careless Whisper The Better Life Rubber Bullets 2 Tons O Fun
    [Show full text]
  • Ace Hood Ft Chris Brown Co Body 2 Body
    Ace Hood ft Chris Brown Body 2 Body Ab g b 4 œ œ œ œ œ œ œ œ œ & b b 4 œ œ œ œ œ œ œ Ba by you dont have to try to read my mind cause you ? b 4 b b 4 ˙ ˙ Bb c Ab g 2 b œ œ œ œ œ œ œ œ œ œ œ & b b œ œ ≈ œ œ œ œ œ œ œ œ œ 2 know I wanna get it in andtell me why we would this think a bout If you ? b b b ˙ ˙ ˙ ˙ Bb c Ab g 4 b & b b œ œ œ œ œ œ. œ œ œ œ œ œ œ œ œ Œ œ œ œ œ œ œ 4 wan na feel my bo dy we can be bo dy to bo dy bodytobo dy ? b b b ˙ ˙ ˙ ˙ Bb c Ab g 6 b & b b œ œ œ œ œ œ œ œ œ œ Œ œ œ œ œ œ œ œ œ œ œ œ œ œ œ 6 I dont nee to rush you girl weshould be bo dy to bo dy bodytobo dy ? b b b ˙ ˙ ˙ ˙ Bb c Ab g 8 b & b b œ œ œ œ œ œ œ Œ ‰ œ œ œ œ. ≈ œ œ œ œ. œ œ œ œ œ 8 bodytobo dy wellma ke love on the floor you kis sing my tat ? b b b ˙ ˙ ˙ ˙ 2 Bb c Bridge Ab g 10 b œ œ œ œ œ œ œ.
    [Show full text]
  • Practices of Polish Butō Dancers
    Interdisciplinary Studies in Performance 14 14 Interdisciplinary Studies in Performance 14 Magdalena Zamorska Magdalena Zamorska Intense Bodily Presence The author explores the practices of Polish buto¯ dancers. Underlining the Magdalena Zamorska Magdalena transcultural potential of the genre, she discusses in particular their individual body-mind practices and so-called buto¯ techniques in order to produce a Intense Bodily Presence generalised account of buto¯ training. Her argument is underpinned by complex field research which she carried out as an expert observer and a workshop Practices of Polish Buto¯ Dancers participant. Drawing on a transdisciplinary approach, which combines insights and findings from the fields of cultural and performance studies, cultural anthropology and cognitive sciences, the book depicts the sequence of three phases which make up the processual structure of buto¯ training: intro, following and embodiment. The Author Magdalena Zamorska is a Ph.D. graduate in Humanities (2012) and an assistant professor at the Institute of Cultural Studies at the University of Wroclaw (Poland). Her research interests include movement, social choreography, issues of perception and reception in choreographic performances. She also explores the intersections of humanities and science. Intense Bodily Presence. Practices of Polish Buto¯ Dancers BodilyIntense Presence. Practices Buto¯ Polish of ISPE-14 276512_Zamorska_TL_151-214 A5HC Fusion.indd 1 08.10.18 15:10 Interdisciplinary Studies in Performance 14 14 Interdisciplinary Studies in Performance 14 Magdalena Zamorska Magdalena Zamorska Intense Bodily Presence The author explores the practices of Polish buto¯ dancers. Underlining the Magdalena Zamorska Magdalena transcultural potential of the genre, she discusses in particular their individual body-mind practices and so-called buto¯ techniques in order to produce a Intense Bodily Presence generalised account of buto¯ training.
    [Show full text]
  • Authorities to Step up Speed Controls at Accident Black Spots on Minor Roads
    FREE COPY THE NEWSPAPER FOR International SOUTHERN SPAIN hockey Official market leader Audited by PGD/OJD delights February 3rd to 9th 2017 www.surinenglish.com Costa crowds Spain, France and Ireland’s News 2 What To Do 42 national teams compete Comment 22 My Home 49 in Malaga and Lifestyle 24 Sport 56 Health & Beauty 34 Classified 62 Benalmádena P60 in English Food & Drink 41 Pastimes 70 BASIL AL BAYATI BRINGS HIS WORLD TO MALAGA The prestigious Iraqi architect has turned an old city centre mansion into a cultural centre due to open in March P8 The architect in one of the rooms of the building soon to open to the public. :: FERNANDO GONZÁLEZ Authorities to step up speed controls at accident black spots on minor roads The traffic authority (DGT) has an- more than the previous year. The A number of nounced plans to install more speed accident rate also increased, espe- stretches in the and surveillance cameras on cially on secondary roads, despite stretches of the regional road net- their volume of traffic being much province of work with high accident rates. The lower than on dual carriageways and move comes in reaction to an in- motorways. New controls to be Malaga have been crease in the road death toll in 2016; brought in include warning signs in the province of Malaga 30 peo- that show the number plate of a pinpointed ple died on the roads, 15 per cent speeding vehicle. P2 Former animal shelter Malaga bar courts Andalusian boss accused of misuse controversy after banning of funds following last customers from entering if health service
    [Show full text]
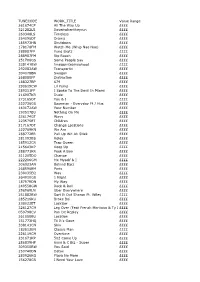
  • TUNECODE WORK TITLE Value Range 261674CP All the Way up Гггг 321282LS Iloveitwhentheyrun Гггг 269348LS Timeless Гггг
    TUNECODE WORK_TITLE Value Range 261674CP All The Way Up ££££ 321282LS Iloveitwhentheyrun ££££ 269348LS Timeless ££££ 254095DT Drama ££££ 185973HN Shutdown ££££ 178176FM Watch Me (Whip Nae Nae) ££££ 288987FP Yung Bratz ££££ 288987FM Rip Roach ££££ 251706GS Some People Say ££££ 338141BW Imsippinteainyohood ££££ 292083AW Transportin ££££ 394078BN Swagon ££££ 268080FP Distraction ££££ 188327BP 679 ££££ 290619CW Lil Pump ££££ 289311FP I Spoke To The Devil In Miami ££££ 216907KR Dude ££££ 273165DT You & I ££££ 222736GU Baseman - Everyday Ft J Hus ££££ 143172AW Your Number ££££ 190517BU Nothing On Me ££££ 236174GT Wavy ££££ 223575ET Children ££££ 217167DT Change Locations ££££ 222769KN We Are ££££ 288772ER Pull Up Wit Ah Stick ££££ 281093BS Rolex ££££ 185912CR Trap Queen ££££ 215643KP Keep Up ££££ 288771KR Peek A Boo ££££ 311205DQ Change ££££ 222206GM Me Myself & I ££££ 306923AN Behind Barz ££££ 268596EM Paris ££££ 239035EQ Way ££££ 264910GU 1 Night ££££ 187979DN My Way ££££ 249558GW Rock & Roll ££££ 256969LN Uber Everywhere ££££ 251882BW Sort It Out Sharon Ft. Wiley ££££ 285216KU Broke Boi ££££ 238022ET Lockjaw ££££ 326127CM Leg Over (Feat French Montana & Ty Dolla)££££ (Remix) 059798CV Pon De Replay ££££ 261050BU Location ££££ 151773HQ Til It's Gone ££££ 338141CN Skin ££££ 182512EN Classic Man ££££ 226119CM Overtime ££££ 231671KP 502 Come Up ££££ 286839HP 6ixvi & C Biz - Super ££££ 309350BW You Said ££££ 250740DN Detox ££££ 280926KQ Playa No More ££££ 156278GR I Need Your Love ££££ 289817KU Slipknot ££££ 318501EW Ski Mask ££££ 156551CN Alright
    [Show full text]
  • Being at Home in One's Body
    Being at home in one’s body Body image in light of identity development Being at home in one’s body Body image in light of identity development Johanna Kling Doctoral Dissertation in Psychology Department of Psychology University of Gothenburg June 5, 2019 © Johanna Kling Cover picture: Charlie Styrbjörn Cover layout: Charlotte Persson Printing: BrandFactory, Gothenburg, Sweden, 2019 ISBN: 978-91-7833-473-5 (PDF) ISBN: 978-91-7833-472-8 (Print) ISSN: 1101-718X Avhandling/Göteborgs universitet, psykologiska inst. Internet link to Gupea: http://hdl.handle.net/2077/60176 Abstract Although the importance of the body to people’s identities has long been theoretically inferred, research linking body image and identity development is scarce. The objective of this thesis was to address this research gap by exploring body image from an identity perspective. Study I aimed to examine how trajectories of body image development from early adolescence to emerging adulthood are related to young people’s sense of identity. A community sample participated from the age of 10 years (N = 967, 53% females) to the age of 24 (N = 542, 56% females). Results of Study I indicated that body image development is connected to sense of iden- tity in emerging adulthood, such that individuals in trajectories with more negative body image displayed less identity coherence. Results also indicated that girls and women (particularly those with higher body mass index) are more likely to display disadvantageous development in terms of more nega- tive body image and more identity problems. The aim of Study II was to explore the many ways in which people might experience their bodies as salient to their identities.
    [Show full text]