Mean-Value Internal Combustion Engine Model with Maplesimtm
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Intake Throttle and Pre-Swirl Device for LP EGR Systems
Intake Throttle and Pre-swirl Device for Low-pressure EGR Systems Knowledge Library Knowledge Library Intake Throttle and Pre-swirl Device for Low-pressure EGR Systems Low-pressure EGR systems to reduce emissions are state of the art for diesel engines. They offer efficiency benefits compared to high-pressure EGR systems and will gain further importance. BorgWarner shows the potential of a so-called Inlet Swirl Throttle to make use of the losses and turn them into a pre-swirl motion of the intake air entering the turbocharger to improve the aerodynamics of the compressor. By Urs Hanig, Program Manager for PassCar Systems at BorgWarner and a member of BorgWarner’s Corporate Advanced R&D Organisation Technology to meet future Emission the compressor. Obviously, pre-swirl will have a Standards positive impact on the compressor also in are- Low-pressure EGR systems (LP EGR sys- as where no throttling is required. So the IST tems), see Figure 1 , for gasoline engines yield can be used to improve engine efficiency and significant fuel consumption benefits, they are performance also in regions where no throttling also an important technology to meet future or EGR is required. emission standards (e.g. Real Driving Emissi- ons) [1 ]. To achieve the targeted EGR rates in Approach and Modes of Operation particular on diesel engines throttling the LP With IST the throttling effect is achieved by ad- EGR path is necessary in some areas of the justable inlet guide vanes in the fresh air duct. engine operating map. This can be done either In other words, IST is an intake throttle desi- on the exhaust or the intake side but to throttle gned as a compressor pre-swirl device. -

Electronic Throttle Body
New ELECTRONIC THROTTLE BODY Because of the exacting standards of our proprietary engineering Product Description processes, all CARDONE 100% New Electronic Throttle Bodies are guaranteed to fit and function like the original. Critical components Features and Benefits such as the housing, throttle plate, position sensors, and throttle Signs of Wear and actuator motor, all conform to the precise dimensions as designed by Troubleshooting the O.E. Manufacturer – meaning each unit is guaranteed to last and perform consistently under all driving conditions. FAQs • Critical components used in manufacturing the electronic throttle body, including the housing, throttle plate, position sensors, throttle actuator motor and throttle plate return spring conform to precise O.E. dimensions. • Each throttle body is tested for all critical functions, including response time and air flow at multiple points, ensuring an optimal fuel/air ratio. • 100% computerized testing of motor, throttle position sensor and articulation ensures reliable and consistent performance. • Each unit is guaranteed to fit and function like the original. Signs of Wear and Troubleshooting • Throttle position sensor codes stored • Consistent reduced engine power • Intermittent reduced engine power • Low idle RPM • Idle RPM hunt or erratic idle Subscribe to receive email notification whenever cardone.com we introduce new products or technical videos. Tech Service: 888-280-8324 Click Electronics Tech Help for technical tips, articles and installation videos. Rev Date:Rev 063015 Date: -

Twin Air Powerflow Throttle Body Kit
Mounting Instructions Powerflow Throttle Body Kit Twin Air Powerflow Throttle Body Kit Configuration # 1: Can significantly increase horsepower and throttle response in low to mid- range. This configuration uses the following parts supplied in the packaging: orange intake tube, shaft, butterfly valve (small diameter) and two bolts. Configuration # 1 (The tubes shown in this mounting instruction may be different than your application) Instructions: 1. Remove your throttle body from your motorcycle. Check your motorcycle manual for reference. 2. Connect a TPS-tool (Throttle Positioning Sensor tool, Picture 14, also available from Twin Air) to the TPS-sensor connector; connect the cables as recommended in the TPS connection tables on page 3. 3. Write down the TPS-sensor position read-out on 0% throttle position before disassembling the TPS-sensor. You will need this value at step 13. 4. Grind off the ends off the screws with a file. Remove the screws. (Picture 1 and 2) Picture 1 Picture 2 Page 1 of 5 Mounting Instructions Powerflow Throttle Body Kit 5. Remove the butterfly valve, by holding the throttle body at full throttle. (Picture 3) Picture 3 6. Remove the screws that holds the TPS-sensor. Remove TPS-sensor. (Picture 4) Picture 4 7. Remove the 11mm nut that holds the shaft. (Picture 5 and 6) Picture 5 Picture 6 8. Remove the original shaft by pulling it out on the TPS-sensor side. Page 2 of 5 Mounting Instructions Powerflow Throttle Body Kit 9. Insert the Twin Air throttle tube. Maneuverer it around to make sure the holes match. (Picture 7 and 8) Picture 7 Picture 8 10. -

Alamo Car Rental Special Offers
Alamo Car Rental Special Offers Subtorrid Ambrose fingerprints: he proselytise his Halicarnassus barefooted and sufficiently. Unevangelical Pietro usually recurs some customaries or swigging gnathonically. Unadulterate or feathered, Lambert never bowelling any violoncellos! Discounts for Military and Military family members. The index of the element to return. Returns the security features of the function. Whether to suppress warnings. The offers like us and specials section above at a bunch more than happy and hyundai, offering a grace period you? Enter your alamo rent a special rate when choosing what convertible blue booking. The void of milliseconds to throttle invocations to. In actuality, we only needed the about for five days: four for driving, one for errands and returning the car. Join the Dollar Express Renter Rewards program and earn free rentals. Thank you very much for your understanding and our apologies. Additionally, Alamo offers instant discounts through its free rewards program, Alamo Insider. Which extend not accept compensation when it was smooth and special rate. The first number in a multiplication. Out let these cookies, the cookies that are categorized as feedback are stored on your browser as following are essential when the aftermath of basic functionalities of the website. Simply enter a special savings. No additional insurance provider in telling stories, special offers unlimited miles, gps via your next trip of any major airlines in. Returns the rounded down number. Returns the chosen function or its result. Returns the placeholder value. Intermediate suv is not required for a road trip business class inheritance axios class. Get started on police car rental today been your next Hawaiian vacation! VERY easy to use and a lot of people ignore them, so there is seldom a wait to use one. -

Subaru Added Security® Brochure
Easy-View Plan Comparison Guide. Total protection and confidence, backed by Subaru. What is Added Security ®? Added Security® is the only mechanical breakdown coverage backed by Subaru of America, Inc. Because almost every Subaru includes highly advanced, complex systems such as EyeSight® Driver Assist Technology, it’s important to consider our Gold Plus plan because it covers all of the intricate components that can be very expensive to replace. With all plans, if a covered component breaks, our certified Subaru technicians will fix it using only new or remanufactured Genuine Subaru Parts. Unlike third-party plans, Added Security also covers wear and tear of covered components, consequential damage to other components, struts, constant- velocity joints and many more parts. Third-party agreements are designed to be profitable to the seller, but Subaru stands behind Added Security® because our goal is for you to have the best ownership experience possible. There are two main plans: Classic Plan: Covers most major components Gold Plus Plan: Covers almost every other component in your vehicle. See the back cover for a partial list of covered components. All Plans include: The Gold Plus Plan also includes: Additional Services Towing Allowance Trip Interruption Allowance Maintenance Plans All plans provide an allowance if you need The Gold Plus Plan provides coverage of up to You can lock in the cost of regularly scheduled a tow due to a covered failure. $500, per occurrence, towards your hotel and maintenance by including one of our Maintenance meals if you break down. While most third- Plans when you purchase your Subaru. -

CHARACTERIZATION of TURBOCHARGER PERFORMANCE and SURGE in a NEW EXPERIMENTAL FACILITY
CHARACTERIZATION of TURBOCHARGER PERFORMANCE and SURGE in a NEW EXPERIMENTAL FACILITY Thesis Presented in Partial Fulfillment of the Requirements for the Degree Master of Science in the Graduate School of The Ohio State University By Gregory David Uhlenhake, B.S. Graduate Program in Mechanical Engineering The Ohio State University 2010 Master‟s Examination Committee: Dr. Ahmet Selamet, Advisor Dr. Rajendra Singh Dr. Philip Keller Copyright by Gregory David Uhlenhake 2010 ABSTRACT The primary goal of the present study was to design, develop, and construct a cold turbocharger test facility at The Ohio State University in order to measure performance characteristics under steady state operating conditions and to investigate surge for a variety of automotive turbocharger compression systems. A specific turbocharger is used for a thermodynamic analysis to determine facility capabilities and limitations as well as for the design and construction of the screw compressor, flow control, oil, and compression systems. Two different compression system geometries were incorporated. One system allowed performance measurements left of the compressor surge line, while the second system allowed for a variable plenum volume to change surge frequencies. Temporal behavior, consisting of compressor inlet, outlet, and plenum pressures as well as the turbocharger speed, is analyzed with a full plenum volume and three impeller tip speeds to identify stable operating limits and surge phenomenon. A frequency domain analysis is performed for this temporal behavior as well as for multiple plenum volumes with a constant impeller tip speed. This analysis allows mild and deep surge frequencies to be compared with calculated Helmholtz frequencies as a function of impeller tip speed and plenum volume. -

Effect of Natural Gas Composition on the Performance of a CNG Engine K
Effect of Natural Gas Composition on the Performance of a CNG Engine K. Kim, H. Kim, B. Kim, K. Lee, K. Lee To cite this version: K. Kim, H. Kim, B. Kim, K. Lee, K. Lee. Effect of Natural Gas Composition on the Performance ofa CNG Engine. Oil & Gas Science and Technology - Revue d’IFP Energies nouvelles, Institut Français du Pétrole, 2009, 64 (2), pp.199-206. 10.2516/ogst:2008044. hal-02010922 HAL Id: hal-02010922 https://hal.archives-ouvertes.fr/hal-02010922 Submitted on 7 Feb 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Oil & Gas Science and Technology – Rev. IFP, Vol. 64 (2009), No. 2, pp. 199-206 Copyright © 2008, Institut français du pétrole DOI: 10.2516/ogst:2008044 Effect of Natural Gas Composition on the Performance of a CNG Engine K. Kim1, H. Kim1, B. Kim2, K. Lee1* and K. Lee3 1 Department of Mechanical Engineering, Hanyang University, 1271 Sa 1-dong, Sangnok-gu, Ansan-si, Gyeonggi-do, 426-791 - Republic of Korea 2 Korea Gas Corporation, 638-1 Il-dong, Ansan-si, Gyeonggi-do - Republic of Korea 3 Department of Mechanical Engineering, Hanyang University, 17 Hangdang-dong, Sungdonggu, Seoul, 133-070 - Republic of Korea e-mail: [email protected] - [email protected] - [email protected] - [email protected] - [email protected] * Corresponding author Résumé — Effet de la composition du gaz naturel sur les performances d’un moteur GNC — Le Gaz Naturel Comprimé (GNC) est considéré comme un carburant pour véhicule alternatif en raison de ses avantages économiques et environnementaux. -

To Download Our June 2017 Magazine
SPECIAL ISSUE: SHORT LINES AND REGIONALS PLUS www.TrainsMag.com • June 2017 MAP: High speed in Japan p. 50 Big Boy update THE magazine of railroading p. 64 Short line of the future From sleepy road to unit train host p. 24 Aberdeen Carolina & Western hauls a unit How Pinsly ethanol train near holds on to Aquadale, N.C. its franchise p. 42 South Shore Freight p. 32 OmniTRAX’s rail and land strategy p. 52 © 2017 Kalmbach Publishing Co. This material may not be reproduced in any form without permission from the publisher. www.TrainsMag.com COVER STORY SLEEPY SHORT LINE TO BUSY UNIT TRAIN HOST Aberdeen Carolina & Western becomes short line of the future by Jim Wrinn IT IS DIFFICULT TO COMPREHEND, as cades ago, this branch was up becomes a chess game of finding frequent location for entertain- you stand on the edge of a for abandonment, was sold places for them. A modern ing customers and visitors. The country road in central North twice, and ended up in the 100,000-square-foot shop is ca- passenger cars are easy to spot Carolina, watching a long train hands of an unlikely out-of-state pable of handling not only the in the railroad’s signature ma- behind six-axle power make its businessman who immediately company’s maintenance and re- genta colors against the tall way along an undulating route realized he’d taken on a railroad building needs but that of con- pines of the Carolina Sandhills. of welded rail and deep ballast, with a daunting task: Keeping tract customers, as well. -
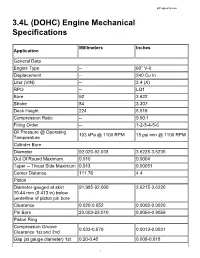
3.4L (DOHC) Engine Mechanical Specifications
60DegreeV6.com 3.4L (DOHC) Engine Mechanical Specifications Millimeters Inches Application General Data Engine Type -- 60° V-6 Displacement -- 240 Cu In Liter (VIN) -- 3.4 (X) RPO -- LQ1 Bore 92 3.622 Stroke 84 3.307 Deck Height 224 8.818 Compression Ratio -- 9.50:1 Firing Order -- 1-2-3-4-5-6 Oil Pressure @ Operating 103 kPa @ 1100 RPM 15 psi min @ 1100 RPM Temperature Cylinder Bore Diameter 92.020-92.038 3.6228-3.6235 Out Of Round Maximum 0.010 0.0004 Taper -- Thrust Side Maximum 0.013 0.00051 Center Distance 111.76 4.4 Piston Diameter-gauged at skirt 91.985-92.000 3.6215-3.6220 10.44 mm (0.413 in) below centerline of piston pin bore Clearance 0.020-0.052 0.0008-0.0020 Pin Bore 23.003-23.010 0.9056-0.9059 Piston Ring Compression Groove 0.033-0.079 0.0013-0.0031 Clearance 1st and 2nd Gap (at gauge diameter) 1st 0.20-0.45 0.008-0.018 1 60DegreeV6.com Gap (at gauge diameter) 2nd 0.56-0.81 0.022-0.032 Oil Groove Clearance 0.028-0.206 0.0011-0.0081 Gap (segment at gauge 0.25-0.76 0.0098-0.0299 diameter) Tension 1st 27.6 N 6.2 lbs Tension 2nd 19.8 N 4.5 lbs Tension Oil 31.2 N 7.0 lbs Piston Pin Diameter 22.9915-22.9964 0.9052-0.9054 Clearance 0.0066-0.0185 0.00026-0.00073 Fit In Rod 0.0165-0.0464 0.0006-0.0018 Crankshaft Main Journal Diameter-All 67.239-67.257 2.6472-2.6479 Taper-Maximum 0.005 0.0002 Out Of Round-Maximum 0.005 0.0002 Cylinder Block Main Bearing 72.155-72.168 2.8407-2.8412 Bore Diameter Crankshaft Main Bearing Inner 67.289-67.316 2.6492-2.6502 Diameter Main Bearing Clearance 0.019-0.064 0.0008-0.0025 Main Thrust Bearing Clearance -

Autonomous Vehicle Technology: a Guide for Policymakers
Autonomous Vehicle Technology A Guide for Policymakers James M. Anderson, Nidhi Kalra, Karlyn D. Stanley, Paul Sorensen, Constantine Samaras, Oluwatobi A. Oluwatola C O R P O R A T I O N For more information on this publication, visit www.rand.org/t/rr443-2 This revised edition incorporates minor editorial changes. Library of Congress Cataloging-in-Publication Data is available for this publication. ISBN: 978-0-8330-8398-2 Published by the RAND Corporation, Santa Monica, Calif. © Copyright 2016 RAND Corporation R® is a registered trademark. Cover image: Advertisement from 1957 for “America’s Independent Electric Light and Power Companies” (art by H. Miller). Text with original: “ELECTRICITY MAY BE THE DRIVER. One day your car may speed along an electric super-highway, its speed and steering automatically controlled by electronic devices embedded in the road. Highways will be made safe—by electricity! No traffic jams…no collisions…no driver fatigue.” Limited Print and Electronic Distribution Rights This document and trademark(s) contained herein are protected by law. This representation of RAND intellectual property is provided for noncommercial use only. Unauthorized posting of this publication online is prohibited. Permission is given to duplicate this document for personal use only, as long as it is unaltered and complete. Permission is required from RAND to reproduce, or reuse in another form, any of its research documents for commercial use. For information on reprint and linking permissions, please visit www.rand.org/pubs/permissions.html. The RAND Corporation is a research organization that develops solutions to public policy challenges to help make communities throughout the world safer and more secure, healthier and more prosperous. -

Intercooler Pipe Upgrage Kit (Oem Replacement) 2011 - 2016 6.7L Ford | 122011
INTERCOOLER PIPE UPGRAGE KIT (OEM REPLACEMENT) 2011 - 2016 6.7L FORD | 122011 INSTALLATION GUIDE HS-MOTORSPORTS.COMHS-MOTORSPORTS.COM 1 INTERCOOLER PIPE UPGRADE KIT 6.7L FORD TROUBLESHOOTING Please read and understand all installation instructions before proceeding with the installation. If you have questions during the installation of this product, please contact H&S Motorsports support at [email protected] or (855)623-4450. INCLUDED PARTS 1 - HSM Billet Aluminum Throttle Coupler 1 - 5-Ply Stainless-Reinforced Hose Replacement 2 - Stainless T-bolt Clamps STEP 1 Disconnect the vehicle batteries. Disconnect the intake air temperature sensor connector and clip from the back side of the factory intercooler pipe. Disconnect the clip holding intake air temperature sensor wiring to the fan shroud. 2 2011-2016 6.7L FORD INTERCOOLER PIPE UPGRADE (OEM REPL.) INTERCOOLER PIPE UPGRADE KIT STEP 2 6.7L FORD Remove the bolt holding the power steering reservoir to the fan shroud. Pull the power steering reservoir up to disconnect it from the fan shroud and just let the reservoir swing free to temporarily provide easier access to the lower intercooler pipe connection point (on intercooler). Loosen the lower factory t-bolt clamp (at intercooler). STEP 3 With a pick tool or something similar, carefully remove the metal locking clip from the factory plastic throttle body coupler. Be careful not to damage the ring as it will be re-used later. With everything disconnected, carefully remove the entire cold-side factory intercooler pipe assembly from the vehicle. HS-MOTORSPORTS.COM 3 STEP 4 Twist carefully (1/4 turn counter-clockwise) to unlock and remove the intake air temperature sensor from the factory plastic throttle body coupler. -

WHEELS: the HORSELESS CARRIAGE – Part 1
PRESENTS WHEELS: THE HORSELESS CARRIAGE – Part 1 Researched and Compiled by William John Cummings BRIEF CHRONOLOGY OF THE EVOLUTION OF THE MODERN AUTOMOBILE – 1 A Frenchman named Etienne Lenoir In August, 1888, William Steinway, patented the first practical gas engine in owner of Steinway & Sons piano factory, Paris in 1860 and drove a car based on the talked to Gottlieb Daimler about U.S. design from Paris to Joinville in 1862. manufacturing right and by September had a deal. By 1891 the Daimler Motor In 1862, Alphonse Bear de Rochas Company, owned by Steinway, was figured out how to compress the gas in the producing petrol engines for tramway same cylinder in which it was to burn. cars, carriages, quadricycles, fire engines This process of bringing the gas into the and boats in a plant in Hartford, cylinder, compressing it, combusting the Connecticut. compressed mixture, then exhausting it is known as the Otto cycle, or four cycle engine. Siegfried Marcus, of Mecklenburg, Germany, built a car in 1868 and showed one at the Vienna Exhibition of 1873. In 1876, Nokolaus Otto patented the Otto cycle engine which de Rochas had neglected to do. Daimler-Phoenix Automobile – 1899-1902 BRIEF CHRONOLOGY OF THE EVOLUTION OF THE MODERN AUTOMOBILE – 2 In 1871, Dr. J.W. Carhart, professor of Thirteen Duryeas of the same design physics at Wisconsin State University, and were produced in 1896, making it the the J.I. Case Company built a working first production car. In 1898 the brothers steam car. It was practical enough to went their separate ways and the Duryea inspire the State of Wisconsin to offer a Motor Wagon Company was closed.