First-Principle Study of Structural, Elastic Anisotropic, And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

University Name Agency Number China Embassy in Tehran 3641
University Name Agency Number China Embassy in Tehran 3641 Aba Teachers College Agency Number 10646 Agricultural University of Hebei Agency Number 10086 Akzo vocational and technical College Agency Number 13093 Anglo-Chinese College Agency Number 12708 Anhui Agricultural University Agency Number 10364 Anhui Audit Vocational College Agency Number 13849 Anhui Broadcasting Movie And Television College Agency Number 13062 Anhui Business College of Vocational Technology Agency Number 12072 Anhui Business Vocational College Agency Number 13340 Anhui China-Australia Technology and Vocational College Agency Number 13341 Anhui College of Traditional Chinese Medicine Agency Number 10369 Anhui College of Traditional Chinese Medicine Agency Number 12924 Anhui Communications Vocational & Technical College Agency Number 12816 Anhui Eletrical Engineering Professional Technique College Agency Number 13336 Anhui Finance & Trade Vocational College Agency Number 13845 Anhui Foreign Language College Agency Number 13065 Anhui Industry Polytechnic Agency Number 13852 Anhui Institute of International Business Agency Number 13846 Anhui International Business and Economics College(AIBEC) Agency Number 12326 Anhui International Economy College Agency Number 14132 Anhui Lvhai Vocational College of Business Agency Number 14133 Anhui Medical College Agency Number 12925 Anhui Medical University Agency Number 10366 Anhui Normal University Agency Number 10370 Anhui Occupatinoal College of City Management Agency Number 13338 Anhui Police College Agency Number 13847 Anhui -

A Complete Collection of Chinese Institutes and Universities For
Study in China——All China Universities All China Universities 2019.12 Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities Anhui 安徽 【www.studyinanhui.com】 1. Anhui University 安徽大学 http://ahu.admissions.cn 2. University of Science and Technology of China 中国科学技术大学 http://ustc.admissions.cn 3. Hefei University of Technology 合肥工业大学 http://hfut.admissions.cn 4. Anhui University of Technology 安徽工业大学 http://ahut.admissions.cn 5. Anhui University of Science and Technology 安徽理工大学 http://aust.admissions.cn 6. Anhui Engineering University 安徽工程大学 http://ahpu.admissions.cn 7. Anhui Agricultural University 安徽农业大学 http://ahau.admissions.cn 8. Anhui Medical University 安徽医科大学 http://ahmu.admissions.cn 9. Bengbu Medical College 蚌埠医学院 http://bbmc.admissions.cn 10. Wannan Medical College 皖南医学院 http://wnmc.admissions.cn 11. Anhui University of Chinese Medicine 安徽中医药大学 http://ahtcm.admissions.cn 12. Anhui Normal University 安徽师范大学 http://ahnu.admissions.cn 13. Fuyang Normal University 阜阳师范大学 http://fynu.admissions.cn 14. Anqing Teachers College 安庆师范大学 http://aqtc.admissions.cn 15. Huaibei Normal University 淮北师范大学 http://chnu.admissions.cn Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities 16. Huangshan University 黄山学院 http://hsu.admissions.cn 17. Western Anhui University 皖西学院 http://wxc.admissions.cn 18. Chuzhou University 滁州学院 http://chzu.admissions.cn 19. Anhui University of Finance & Economics 安徽财经大学 http://aufe.admissions.cn 20. Suzhou University 宿州学院 http://ahszu.admissions.cn 21. -

University of Leeds Chinese Accepted Institution List 2021
University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams. -

CGS) Merupakan Beasiswa Full Untuk Meneruskan Jenjang Pendidikan Magister Di Shanghai Normal University Dari Tahun 2016 Sampai Dengan Saat Ini
Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok Beasiswa pertama yang ia peroleh dari Chinese Government Scholarships (CGS) merupakan beasiswa full untuk meneruskan jenjang pendidikan magister di Shanghai Normal University dari tahun 2016 sampai dengan saat ini. Belajar dan tinggal di negeri China merupakan cita-cita kecilnya semenjak usia 6 tahun. Karena ia terinspirasi dari hadits Nabi Muhammad SAW yang berbunyi, “Uthlubul ilma walau bisshin” yang artinya, “Carilah ilmu sampai ke negeri China”. 0 | H a l a m a n Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok 1 | H a l a m a n Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok PPI Tiongkok mempersembahkan PANDUAN KULIAH DI CHINA Edisi 2017 Penulis: Nurul Juliati Putra Wanda Ahmad Fahmi Putri Aris Safitri Tirta anhari Editor: Fadlan Muzakki, Sitti Marwah, Marilyn Janice 2 | H a l a m a n Departemen Pendidikan dan Pengembangan Organisasi Perhimpunan Pelajar Indonesia (PPI) Tiongkok Sambutan Ketua PPI Tiongkok Salam sejahtera untuk kita semua. Ada pepatah yang mengatakan hidup itu harus menjadi garam dan terang bagi dunia. atas dasar itulah PPI Tiongkok ada, yaitu memberikan kontribusi positif bagi Indonesia. PPI Tiongkok sebagai wadah pengembangan minat dan bakat mahasiswa Indonesia memegang peranan penting dalam mempersatukan para pelajar Indonesia di Tiongkok. salah satu misi kami adalah agar para pelajar Indonesia tidak lupa dengan bangsanya sendiri dan suatu saat nanti bisa pulang untuk membangun Indonesia. Oleh karena itu visi Kabinet KB (keluarga berencana) PPI Tiongkok tahun ini adalah memperkuat hubungan internal antar pengurus dan juga meningkatkan kesinergian antara PPIT Cabang. kami yakin dengan hubungan internal yang solid, bahkan hingga mampu menjadi seperti keluarga, ditambah dengan perencanaan yang matang, PPI Tiongkok dapat menghasilkan inisiatif-inisiatif yang dapat berdampak positif bagi mahasiswa-mahasiswa Indonesia yang ada di Tiongkok. -

Ex-Post Project Evaluation 2010 Package IV-2 (Indonesia, China, Nepal)
Ex-Post Project Evaluation 2010 Package IV-2 (Indonesia, China, Nepal) October 2011 JAPAN INTERNATIONAL COOPERATION AGENCY International Development Center of Japan Incorporated OPMAC Corporation EVD JR 11-51 Preface Ex-post evaluation of ODA projects has been in place since 1975 and since then the coverage of evaluation has expanded. Japan’s ODA charter revised in 2003 shows Japan’s commitment to ODA evaluation, clearly stating under the section “Enhancement of Evaluation” that in order to measure, analyze and objectively evaluate the outcome of ODA, third-party evaluations conducted by experts will be enhanced. This volume shows the results of the ex-post evaluation of ODA Loan projects that were mainly completed in fiscal year 2008, and Technical Cooperation projects and Grant Aid projects, most of which project cost exceeds 1 billion JPY, that were mainly completed in fiscal year 2007. The ex-post evaluation was entrusted to external evaluators to ensure objective analysis of the projects’ effects and to draw lessons and recommendations to be utilized in similar projects. The lessons and recommendations drawn from these evaluations will be shared with JICA’s stakeholders in order to improve the quality of ODA projects. Lastly, deep appreciation is given to those who have cooperated and supported the creation of this volume of evaluations. October 2011 Masato Watanabe Vice President Japan International Cooperation Agency (JICA) Disclaimer This volume of evaluations, the English translation of the original Japanese version, shows the result of objective ex-post evaluations made by external evaluators. The views and recommendations herein do not necessarily reflect the official views and opinions of JICA. -
1 Please Read These Instructions Carefully
PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • The Program Category is Type B. • The Agency No. matches the university you will be attending. See Appendix A for a list of the Chinese university agency numbers. • Use the + by each section to expand on that section of the form. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. Contact your home or host university coordinator to find out when you will receive your admission documents. Contact information for you home university CLIC liaison can be found here: http://clicstudyinchina.com/contact-us/ 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies. -

Research on the Construction Path of the First-Class Major of Journalism in Shaanxi Universities Under the Concept of Educational Certification
2019 5th International Conference on Education Technology, Management and Humanities Science (ETMHS 2019) Research on the Construction Path of the First-class Major of Journalism in Shaanxi Universities under the Concept of Educational Certification Fang Zhang Xi’an Peihua University, Xi'an, Shaanxi, 710125, China Keywords: Higher Vocational Colleges; English; Informatization; Teaching Model; Abstract: The major of journalism has been a little unpopular in recent year. With the development of network technology and new media technology, the admission score of journalism is increasing day by day. The development of news communication industry is more vigorous, and the professional requirement of news talents with new media literacy is higher. In the future, the gap of high-quality journalism talents is very big. However, the competition for talents in China’s journalism industry has been fierce since China joined the World Trade Organization, the employment of journalism majors in recent years is not optimistic, and even the cities with developed media industry are showing a downward trend of employment rate. Therefore, colleges and universities need to speed up the reform and innovation of journalism. Based on the concept of education certification, this paper studies the construction path of first-class journalism major in Shaanxi colleges and universities. 1. Introduction First-rate majors mean that the Ministry of Education aims at building top-class majors, which are oriented to the future, adapts to the needs, leads the development, has advanced ideas and guarantees the strength of the first-class specialty. Major is the basic unit and basic platform of talent training, to build first-class undergraduate course and train first-class talents. -

Click Here to Download Full Papers
Copyright © 2013 by Society of International Chinese in Educational Technology (SICET) All rights reserved. No part of this book may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior written permission of the publisher. SICET is not responsible for papers accidentally omitted form the conference proceedings due to late or errant submission by the author or proxy, or technical electronic anomalies during the time of submission. The publisher is not responsible for the use which might be made of the information contained in this book. From SICET, the Conference Organizer: This is to confirm that all conference paper submissions are peer-reviewed by at least two referees prior to acceptance in the Final Program and prior to publication in the Proceedings book. Published by Society of International Chinese in Educational Technology (SICET) 118 College Dr. #5057 Hattiesburg, MS 39406 USA http://sicet.org ISBN: 2168-944X (Print); ISSN: 2166-0549 (Online) Printed at Tsinghua University, Beijing, China Special thanks to – EITT 2013 host universities: Educational Technology Institute (THETI), Tsinghua University, China and the Center for Instructional Technology Solutions in Industry and Education (CITSIE), Virginia Tech, USA About EITT 2013 The Second International Conference of Educational Innovation through Technology (EITT 2013) provides a forum for researchers who study technology and education to publish research findings and exchange experiences in related topics. The conference is organized by Society of International Chinese in Educational Technology (SICET). It is hosted jointly by Tsinghua University and Virginia Tech. It collaborates with the annual Educational Technology Leadership Conference (ETLC) which is sponsored by Virginia Tech's Center for Instructional Technology Solutions in Industry and Education. -
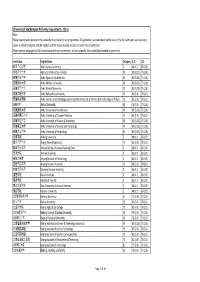
University of Southampton PGT Entry Requirements ‐ China Note: These Requirements Represent the Standard Entry Criteria for Our Programmes
University of Southampton PGT entry requirements ‐ China Note: These requirements represent the standard entry criteria for our programmes. All applications are considered on the basis of the full submission, and so strong scores in relevant subjects and the suitability of the course studied will also be taken into consideration. Please see our webpages for full information and entry requirements, including specific School and Departmental requirements. Institution English Name Category 2:1 2:2 阿坝师范学院 Aba Teachers University Z 88 (3.7) 83 (3.5) 河北农业大学 Agricultural University of Hebei X3 80 (3.25) 75 (2.8) 安徽农业大学 Anhui Agricultural University X3 80 (3.25) 75 (2.8) 安徽医科大学 Anhui Medical University X3 80 (3.25) 75 (2.8) 安徽师范大学 Anhui Normal University X3 80 (3.25) 75 (2.8) 安徽工程大学 Anhui Polytechnic University Y2 83 (3.5) 78 (3.1) 安徽科技学院 Anhui Science and Technology University (AKA University of Science And Technology of Anhui) Y2 83 (3.5) 78 (3.1) 安徽大学 Anhui University X2 78 (3.1) 73 (2.6) 安徽建筑大学 Anhui University of Architecture X3 80 (3.25) 75 (2.8) 安徽中医药大学 Anhui University of Chinese Medicine Y2 83 (3.5) 78 (3.1) 安徽财经大学 Anhui University of Finance & Economics X3 80 (3.25) 75 (2.8) 安徽理工大学 Anhui University of Science and Technology X3 80 (3.25) 75 (2.8) 安徽工业大学 Anhui University of Technology X3 80 (3.25) 75 (2.8) 安康学院 Ankang University Z 88 (3.7) 83 (3.5) 安庆师范大学 Anqing Normal University Y2 83 (3.5) 78 (3.1) 鞍山师范学院 Anshan Normal University Liaoning China Z 88 (3.7) 83 (3.5) 安顺学院 Anshun University Z 88 (3.7) 83 (3.5) 安阳工学院 Anyang Institute of Technology -

CONICYT Ranking Por Disciplina > Sub-Área OECD (Académicas) Comisión Nacional De Investigación 2
CONICYT Ranking por Disciplina > Sub-área OECD (Académicas) Comisión Nacional de Investigación 2. Ingeniería y Tecnología > 2.2 Ingeniería Eléctrica y Electrónica Científica y Tecnológica PAÍS INSTITUCIÓN RANKING PUNTAJE CHINA Tsinghua University 1 5,000 INDIA Indian Institute of Technology System (IIT System) 2 5,000 Nanyang Technological University & National Institute of Education SINGAPORE 3 5,000 (NIE) Singapore USA Massachusetts Institute of Technology (MIT) 4 5,000 CHINA Harbin Institute of Technology 5 5,000 USA Georgia Institute of Technology 6 5,000 FRANCE Universite Paris Saclay (ComUE) 7 5,000 USA Carnegie Mellon University 8 5,000 CHINA Shanghai Jiao Tong University 9 5,000 CHINA Southeast University - China 10 5,000 USA University of California Berkeley 11 5,000 CHINA Zhejiang University 12 5,000 SINGAPORE National University of Singapore 13 5,000 SWITZERLAND ETH Zurich 14 5,000 CHINA University of Electronic Science & Technology of China 15 5,000 DENMARK Aalborg University 16 5,000 USA University of Michigan 17 5,000 CHINA Huazhong University of Science & Technology 18 5,000 CHINA Beihang University 19 5,000 GERMANY Technical University of Munich 20 5,000 SWITZERLAND Ecole Polytechnique Federale de Lausanne 21 5,000 USA Stanford University 22 5,000 CHINA Peking University 23 5,000 USA University of Illinois Urbana-Champaign 24 5,000 CHINA Beijing University of Posts & Telecommunications 25 5,000 CHINA Xidian University 26 5,000 UNITED KINGDOM Imperial College London 27 5,000 USA University of Texas Austin 28 5,000 USA University -

List of Regular Institutions of Higher Education In
Table 1 List of Regular Institutions of Higher Education in China (As of May 23th, 2011) (Total number:820) Serial Level of Name of Institution Affiliation Location Remarks No. -

Study on the Graduate Employability of Chinese Regional Public Universities (Primarily Teaching-Oriented)
Jin TAO STUDY ON THE GRADUATE EMPLOYABILITY OF CHINESE REGIONAL PUBLIC UNIVERSITIES (PRIMARILY TEACHING-ORIENTED) Faculty of Management and Business Master Thesis March 2021 ABSTRACT Jin TAO: Study on the Graduate Employability of Chinese Regional Public Universities (Primarily Teaching- oriented) Master Thesis Tampere University Master’s Programme in Research and Innovation in Higher Education March 2021 Employment of university graduates is an important issue that the society pays close attention to. With the expansion of China’s higher education system, the employment situation of graduates from regional public higher education institutions (primarily teaching-oriented) has become increasingly severe. In the meantime, research on the employability of regional public university graduates remain underdeveloped. This paper carried out a two-phased mixed-methods empirical research to explore the graduate employability of regional public HEIs. Specifically, a quantitative survey was employed among 729 graduates of Xi’an University; 12 interviews were conducted with staff from Xi’an University, Baoji University of Arts and Sciences, Yulin University and Ankang University, which locate in different regions of Shaanxi Province. Overall, the analysis results showed that personal qualities and generic skills are the most important components of graduate employability, and university’s strategy has the greatest significance on graduate employability. A graduate employability model was further developed based on findings of the data. Keywords: