DOCSLIB.ORG

Regular Mappings and Marvel Temperaments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Regular Mappings and Marvel Temperaments Regular Mappings and Marvel Temperaments Graham Breed This is the annotated version of the slides for the presentation I gave at Beyond the Semitone in Aberdeen, October 2013. The annotations cover things I said, or should have said, or might have said if I’d had more time. 0.1 Motivation Goals of Regular Temperament Regular temperaments are systems that approximate just intonation using fewer notes. This assumes there’s something special about just intonation that you want to preserve, and if you don’t feel this, temperament won’t be useful to you. The ”regular” part means each just ratio is tuned in a consistent way, and more than one just ratio will typically approximate to the same tempered interval. The list below is roughly prioritized, and the tuning is the least important thing. There’s a trap in microtonal literature that you focus on the tuning, and people think it’s all about tuning, although the tuning is only a tool in the service of exploring new harmonies, or making just intonation scales more manageable. • New harmonic systems • Frugal scales • Notation • Generalized keyboards • Tuning Beyond Temperament These ideas come from the study of temperaments, but can still be useful if you don’t use temperament. This is why I talk about a ”regular mapping paradigm” rather than ”regular temperament theory”. 1 I added some citations for the academic audience, and also to avoid giving the impression that everything I was talking about was original to me. Christian Kaernbach, who gave the talk after mine, discussed the idea that musicians might not play the (simplistic) theoretically correct pitches, and that doesn’t mean they’re wrong. That fortuitously agrees with my first point here. • Support flexible pitch instruments. • Leave the tuning as just intonation. (Fokker 1969) • Write just intonation as tempered notation. (Secor 1975) The mapping from just to tempered pitches remains. What Took So Long? This is the defeatist slide that excuses why everybody isn’t using these temper- aments and related techniques already. It furthers my agenda regarding the regular mapping paradigm in that part of Kuhn’s description of paradigm shifts is about the resistance that a new paradigm encounters. It’s also worth pointing out that these ideas won’t be equally valuable to everybody. • New pitches are disruptive. • Meantone is good. • Not all music needs pure harmony. • Good mappings are easy to recognize but hard to find. • Computers make searches and tuning easier. 0.2 Theory The Marvel Mapping Tempering out 225:224 (7.7 cents) relates the 7th harmonic partial to two fifths and two thirds. These lattice diagrams show how the prime number 7 ties into the 5-limit lattice. With proper spelling, the 7 should be written as an augmented sixth rather than a minor seventh. (You may choose to add a diesis¨ accidental so that the 7 can be a kind of seventh.) 2 Because the 7.7 cents get shared out among four 5-limit intervals, each 7-limit interval can be tuned to within 2 cents, which will sound as good as just intonation in most contexts. I copied the diagrams from my Tripod Notation document. The thirds are shown shorter than the fifths so that subminor thirds giving magic approxima- tions don’t end up as huge triangles. Without showing magic approximations, the triangles should be roughly equilateral, but it doesn’t really matter. 14 5 4 6 9 A] E (F]) C G D Interval Arithmetic I like equations, so I had to bring some equations into my music theory talk. Each shows a musical relationship, and in each case the equations fail to be exact by the 225:224 that’s being tempered out. The first is an augmented triad showing two 5:4 major thirds and a 9:7 su- permajor third adding up to an octave. (Intervals add where fractions multiply.) The Wikipedia page on augmented triads mentions the 225:224, so it must be standard theory. The second equation ties the new septimal interval to familiar extended 5-limit intervals including the larger whole tone of 9:8. The third equation is the same but with the 9:8 split into two 3:2 fifths, and covers another octave. This is the equation that describes the lattices on the previous slide. Finally, we can see that two diatonic semitones approximate to being the same. This means that you can take any marvel temperament, pile up two semitones, and call the result an 8:7. In fact, you can do more than see. You can hear audio examples of these equations in ”fractions.pdf” in the accompanying bundle. For each equation, notes of an ascending scale overlap to give each dyad on the left hand side and then the first note comes back to give the right hand dyad. 3 5 5 9 2 × × ≈ 4 4 7 1 5 5 9 7 × × ≈ 4 4 8 4 5 5 3 3 7 × × × ≈ 4 4 2 2 2 16 15 ≈ 15 14 Question This was an attempt to catch the audience out, but they were too canny and asked what kind of semitone I was asking about. How may semitones are there to an octave? The point about focusing on semitones was partly to subvert the ”beyond” in the conference title, but also to show that we’re expecting generalzed diatonics of around 10 notes. I could have put this at the introduction to miracle temperament, but I decided to have it to introduce the step size list instead. Answer I showed the logarithms so that people can see how easy the calculations are. The last one is the geometric mean of the two just intervals. It’s a rough approximation of the optimal marvel semitone. log(2) 15 = 10:04 ::: log 14 log(2) 16 = 10:74 ::: log 15 log(2) 2 8 = 10:38 ::: log 7 Scale Sizes These are scale sizes rather than equal temperaments so that I don’t have to worry about ambiguous mappings. (Where there’s ambiguity, this is the 4 marvel option.) It also helps draw attention to the small numbers that represent diatonics rather than tunings. 10 and 9 both come out better than 7, so we might still expect 7 note diatonics, but also 9 and 10 note scales. For a bit more complexity, 12 is very good. There’s a notable absence of pentatonics. This is because the things that make pentatonics good in a 5-limit context put 10 and 15 into this list, but 5 itself doesn’t work so well in the 7-limit. The ranking follows cangwu badness with a dimensionless parameter of 0.001. This gives simpler scales than the default my Python module uses, and means pajara gets near the top of the rank 2 list later on. It also gives 19 as the number one division to tie in with Graham Hair’s work that was featured at the conference. I filtered out temperaments with contorsion (where each JI approximation is an even number, or something like that) because they aren’t very interesting. A lot of the information in the list ties in with that rank 2 list. If you can compare the two, you may like to do so. Note that the top three are all meantones. 19 can than pair with 41 or 22 to give magic. You can find multiple representatives of the other top rank 2 classes in the top row. The bottom row is less interesting. Because I don’t target excessively small errors, near-optimal tunings for planar marvel don’t show up. If you want one, you could try 269. The planar audio examples use 1273 ”marvel cents” to the octave. This week’s Marvel Top 40: 19 31 12 41 22 53 10 72 50 9 34 29 7 60 43 3 84 63 65 21 2 94 91 75 32 51 28 103 48 15 40 69 81 46 113 17 79 26 16 74 0.3 Harmony Substituted Dominant Cadences These audio examples (sdc.mp3) are to illustrate the use of tempered augmented triads. They’re written in musical notation, but they aren’t musical examples. They only show some chord progressions you could use to build music out of. What I know about augmented triads is that you can use one to connect any chord to any other chord. So, given that, I don’t know what a typical progression 5 would be to use as an example. I thought about finding one in Gesualdo, to tie in with some other things at the conference, but that would have meant work so instead I went to Wikipedia. That mentioned this ii-V-I progression with the V substituted. The accidentals are mixed 72-tone Sagittal. The sharp hooks are commas and the more rounded hooks are larger deviations. The first example has the augmented triad written as two consecutive 5-limit thirds. That’s the way Wikipedia writes it, but in marvel I find it the worst tuning. The whole chord covers an interval of 14:9 which isn’t very digestible. In the second example, the higher third is a 9:7 approximation. The chord as a whole covers 8:5. This is the best version if you like 5-limit intervals from the root. The final example has the 9:7 as the lower interval. That’s the best version if you like chords that imitate the large/small pattern of a major triad. Whether or not that’s important, it sounds fine because the span is still 8:5.
Load more

Recommended publications
  • The 17-Tone Puzzle — and the Neo-Medieval Key That Unlocks It
    The 17-tone Puzzle — And the Neo-medieval Key That Unlocks It by George Secor A Grave Misunderstanding The 17 division of the octave has to be one of the most misunderstood alternative tuning systems available to the microtonal experimenter. In comparison with divisions such as 19, 22, and 31, it has two major advantages: not only are its fifths better in tune, but it is also more manageable, considering its very reasonable number of tones per octave. A third advantage becomes apparent immediately upon hearing diatonic melodies played in it, one note at a time: 17 is wonderful for melody, outshining both the twelve-tone equal temperament (12-ET) and the Pythagorean tuning in this respect. The most serious problem becomes apparent when we discover that diatonic harmony in this system sounds highly dissonant, considerably more so than is the case with either 12-ET or the Pythagorean tuning, on which we were hoping to improve. Without any further thought, most experimenters thus consign the 17-tone system to the discard pile, confident in the knowledge that there are, after all, much better alternatives available. My own thinking about 17 started in exactly this way. In 1976, having been a microtonal experimenter for thirteen years, I went on record, dismissing 17-ET in only a couple of sentences: The 17-tone equal temperament is of questionable harmonic utility. If you try it, I doubt you’ll stay with it for long.1 Since that time I have become aware of some things which have caused me to change my opinion completely.
    [Show full text]
  • August 1909) James Francis Cooke
    Gardner-Webb University Digital Commons @ Gardner-Webb University The tudeE Magazine: 1883-1957 John R. Dover Memorial Library 8-1-1909 Volume 27, Number 08 (August 1909) James Francis Cooke Follow this and additional works at: https://digitalcommons.gardner-webb.edu/etude Part of the Composition Commons, Ethnomusicology Commons, Fine Arts Commons, History Commons, Liturgy and Worship Commons, Music Education Commons, Musicology Commons, Music Pedagogy Commons, Music Performance Commons, Music Practice Commons, and the Music Theory Commons Recommended Citation Cooke, James Francis. "Volume 27, Number 08 (August 1909)." , (1909). https://digitalcommons.gardner-webb.edu/etude/550 This Book is brought to you for free and open access by the John R. Dover Memorial Library at Digital Commons @ Gardner-Webb University. It has been accepted for inclusion in The tudeE Magazine: 1883-1957 by an authorized administrator of Digital Commons @ Gardner-Webb University. For more information, please contact [email protected]. AUGUST 1QCQ ETVDE Forau Price 15cents\\ i nVF.BS nf//3>1.50 Per Year lore Presser, Publisher Philadelphia. Pennsylvania THE EDITOR’S COLUMN A PRIMER OF FACTS ABOUT MUSIC 10 OUR READERS Questions and Answers on the Elements THE SCOPE OF “THE ETUDE.” New Publications ot Music By M. G. EVANS s that a Thackeray makes Warrington say to Pen- 1 than a primer; dennis, in describing a great London news¬ _____ _ encyclopaedia. A MONTHLY JOURNAL FOR THE MUSICIAN, THE THREE MONTH SUMMER SUBSCRIP¬ paper: “There she is—the great engine—she Church and Home Four-Hand MisceUany Chronology of Musical History the subject matter being presented not alpha¬ Price, 25 Cent, betically but progressively, beginning with MUSIC STUDENT, AND ALL MUSIC LOVERS.
    [Show full text]
  • Fomrhi-110.Pdf
    v^uaneny INO. nu, iNovcmDer ^uuo FoMRHI Quarterly BULLETIN 110 Christopher Goodwin 2 COMMUNICATIONS 1815 On frets and barring; some useful ideas David E McConnell 5 1816 Modifications to recorder blocks to improve sound production Peter N Madge 9 1817 What is wrong with Vermeer's guitar Peter Forrester 20 1818 A new addition to the instruments of the Mary Rose Jeremy Montagu 24 181*9 Oud or lute? - a study J Downing 25 1820 Some parallels in the ancestry of the viol and violin Ephraim Segerman 30 1821 Notes on the polyphont Ephraim Segerman 31 1822 The 'English' in English violette Ephraim Segerman 34 1823 The identity of tlie lirone Ephraim Segerman 35 1824 On the origins of the tuning peg and some early instrument name:s E Segerman 36 1825 'Twined' strings for clavichords Peter Bavington 38 1826 Wood fit for a king? An investigation J Downing 43 1827 Temperaments for gut-strung and gut-fretted instruments John R Catch 48 1828 Reply to Hebbert's Comm. 1803 on early bending method Ephraim Segerman 58 1829 Reply to Peruffo's Comm. 1804 on gut strings Ephraim Segerman 59 1830 Reply to Downing's Comm. 1805 on silk/catgut Ephraim Segerman 71 1831 On stringing of lutes (Comm. 1807) and guitars (Comms 1797, 8) E Segerman 73 1832 Tapered lute strings and added mas C J Coakley 74 1833 Review: A History of the Lute from Antiquity to the Renaissance by Douglas Alton Smith (Lute Society of America, 2002) Ephraim Segerman 77 1834 Review: Die Renaissanceblockfloeten der Sammlung Alter Musikinstrumenten des Kunsthistorisches Museums (Vienna, 2006) Jan Bouterse 83 The next issue, Quarterly 111, will appear in February 2009.
    [Show full text]
  • Information to Users
    INFORMATION TO USERS This manuscript has been reproduced from the microfihn master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely afreet reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps. Each original is also photographed in one exposure and is included in reduced form at the back of the book. Photographs included in the original manuscript have been reproduced xerographically in this copy. Higher quality 6" x 9" black and white photographic prints are available for any photographs or illustrations appearing in this copy for an additional charge. Contact UMI directly to order. UMI University Microfilms International A Bell & Howell Information Company 3 0 0 North Z eeb Road. Ann Arbor. Ml 48106-1346 USA 313/761-4700 800/521-0600 Order Number 9401386 Enharmonicism in theory and practice in 18 th-century music Telesco, Paula Jean, Ph.D. The Ohio State University, 1993 Copyright ©1993 by Telesco, Paula Jean.
    [Show full text]
  • Universal Tuning Editor
    Universal Tuning Editor Ηπ INSTRUMENTS Aaron Andrew Hunt Ηπ INSTRUMENTS hpi.zentral.zone · Universal Tuning Editor · documentation v11 1.May.2021 Changes from Previous Documentation 5 Current Version, v11 — 1. May 2021 ....................................................................5 Previous Versions ............................................................................................5 Introduction 9 Features List .................................................................................................9 User Interface Basics ......................................................................................11 Maximising the Detail View ..............................................................................12 Maximising the Tuning List ..............................................................................13 Toolbar .......................................................................................................13 Bug Reporting & Feedback ...............................................................................14 Feature Requests ..........................................................................................14 File Handling 15 Preferences ..................................................................................................15 Auto store unsaved projects internally ...............................................................15 Restore external projects at next session ...........................................................15 Prompt to handle each open project
    [Show full text]
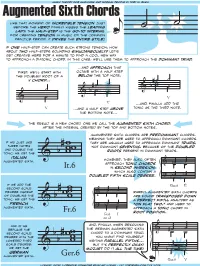
  • Augmented Sixth Chords Are Predominant Chords, Meaning They Are Used to Approach Dominant Chords
    Augmentedmusic Sixth theory for musicians Chords and normal people by toby w. rush like that moment of incredible tension just before the hero finally kisses the leading lady, the half-step is the go-to interval for creating tension in music of the common ˙ practice period. it drives the entire style! ˙ if one half-step can create such strong tension, how about two half-steps sounding simultaneously? Let’s get creative here for a minute to find a cool new way to approach a diatonic chord. in this case, we’ll use them to approach the dominant triad. ...and approach that first, we’ll start with octave with a half step the doubled root of a below the top note, V chord... #˙ ˙ #˙ ˙ ˙ ˙ & b ˙ ˙ & b ˙ ˙ V & ˙ V ...and, finally, add the V ...and a half step above tonic as the third note. the bottom note... the result is a new chord, one we call the augmented sixth chord, after the interval created by the top and bottom notes. augmented sixth chords are predominant chords, meaning they are used to approach dominant chords. if we just use they are usually used to approach dominant triads, three notes not dominant sevenths, because of the doubled and double the roots present in dominant triads. tonic, we get the #w italian ww however, they also often augmented sixth. b w & approach tonic chords & #˙ ˙ It.6 in second inversion, ˙ ˙ which also contain a doubled fifth scale degree. ? b˙ n˙ b ˙ ˙ if we add the 6 Ger.6 I4 second scale degree instead ˙ ˙ rarely, augmented sixth chords of doubling the # w & ˙ ˙ are found transposed down tonic, we get the ww a perfect fifth, analyzed as french b w ˙ ˙ “on flat two,” and used to augmented sixth.
    [Show full text]
  • The Augmented Sixth Chord
    CHAPTER24 The Augmented Sixth Chord Characteristics, Derivation, and Behavior The two excerpts in Example 24.1 are from different style periods, yet they share several features. In terms of form and harmony, both divide into two subphrases and close with strong half cadences. Further, the pre-dominant harmony in both examples is the same: an altered iv6 chord. Indeed, we hear not a Phrygian cadence (iv6-V), but rather some chromatic version, where the diatonic major sixth above the bass is raised a half step to create the strongly directed interval of the augmented sixth (+6). The new half-step ascent (#4-5) mirrors the bass's half-step descent (6-5). We refer to such chromatic pre-dominants as augmented sixth chords because of the characteristic interval between the bass 6 and the upper-voice #4. Listen to both excerpts in Example 24.1, noting the striking sound of the augmented sixth chords. EXAMPLE 24.1 A. Schubert, WaltzinG minor, Die letzte Walzer, op. 127, no. 12, D. 146 472 CHAPTER 24 THE AUGMENTED SIXTH CHORD 473 B. Handel, "Since by Man Came Death," Messiah, HWV 56 Example 24.2 demonstrates the derivation of the augmented sixth chord from the Phrygian cadence. Example 24.2A represents a traditional Phrygian half cadence. In Example 24.2B, the chromatic F# fills the space between F and G, and the passing motion creates an interval of an augmented sixth. Finally, Example 24.2C shows the augmented sixth chord as a harmonic entity, with no consonant preparation. EXAMPLE 24.2 Phrygian Cadence Generates the Augmented Sixth Chord Given that the augmented sixth chord also occurs in major, one might ask if it is an example of an applied chord or a mixture chord? To answer this question, consider the diatonic progression in Example 24.3A.
    [Show full text]
  • Tuning Continua and Keyboard Layouts
    October 4, 2007 8:34 Journal of Mathematics and Music TuningContinua-RevisedVersion Journal of Mathematics and Music Vol. 00, No. 00, March 2007, 1–15 Tuning Continua and Keyboard Layouts ANDREW MILNE∗ , WILLIAM SETHARES , and JAMES PLAMONDON † ‡ § Department of Music, P.O. Box 35, FIN-40014, University of Jyvaskyl¨ a,¨ Finland. Email: [email protected] † 1415 Engineering Drive, Dept Electrical and Computer Engineering, University of Wisconsin, Madison, WI 53706 USA. ‡ Phone: 608-262-5669. Email: [email protected] CEO, Thumtronics Inc., 6911 Thistle Hill Way, Austin, TX 78754 USA. Phone: 512-363-7094. Email: § [email protected] (received April 2007) Previous work has demonstrated the existence of keyboard layouts capable of maintaining consistent fingerings across a parameterised family of tunings. This paper describes the general principles underlying layouts that are invariant in both transposition and tuning. Straightforward computational methods for determining appropriate bases for a regular temperament are given in terms of a row-reduced matrix for the temperament-mapping. A concrete description of the range over which consistent fingering can be maintained is described by the valid tuning range. Measures of the resulting keyboard layouts allowdirect comparison of the ease with which various chordal and scalic patterns can be fingered as a function of the keyboard geometry. A number of concrete examples illustrate the generality of the methods and their applicability to a wide variety of commas and temperaments, tuning continua, and keyboard layouts. Keywords: Temperament; Comma; Layout; Button-Lattice; Swathe; Isotone 2000 Mathematics Subject Classification: 15A03; 15A04 1 Introduction Some alternative keyboard designs have the property that any given interval is fingered the same in all keys.
    [Show full text]
  • Augmented 6Ths
    TutorTube: Augmented 6ths Summer 2020 Introduction Hello and welcome to TutorTube, where The Learning Center’s Lead Tutors help you understand challenging course concepts with easy to understand videos. My name is Darren Churn, Lead Tutor for Music Theory. In today’s video, we will explore Augmented 6ths. Let’s get started. Augmented 6ths Augmented 6th chords are appropriately named due to the fact that they contain an Augmented 6th interval. They are used most commonly as predominant chords that resolve to the dominant. Augmented 6ths are not written as roman numerals like most chords you would analyze. Instead, the chord is identified as one of three types of augmented chords: Italian, French, and German. These chords can be found in major or minor keys and each of these types uses the same solfege base of Le Do Fi. The solfege refers to a lowered 6th scale degree (Le), the tonic (Do), and a raised 4th (Fi) scale degree. Our augmented 6th interval is between the Le and the Fi. Let’s look at the specific types. Italian The first type of augmented 6th chord is Italian. Italian augmented 6ths are the only chords in this category that are not 7th chords. In an Italian chord, we still have our base of Le, Do, Fi. The last note that we add simply doubles Do. This example that we have is based in the key of C. Our Le will be Ab, our Do will be C, and our Fi will be F#. Since this is an Italian chord, we will simply add another C to double the Do.
    [Show full text]
  • The Death and Resurrection of Function
    THE DEATH AND RESURRECTION OF FUNCTION A Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By John Gabriel Miller, B.A., M.C.M., M.A. ***** The Ohio State University 2008 Doctoral Examination Committee: Approved by Dr. Gregory Proctor, Advisor Dr. Graeme Boone ________________________ Dr. Lora Gingerich Dobos Advisor Graduate Program in Music Copyright by John Gabriel Miller 2008 ABSTRACT Function is one of those words that everyone understands, yet everyone understands a little differently. Although the impact and pervasiveness of function in tonal theory today is undeniable, a single, unambiguous definition of the term has yet to be agreed upon. So many theorists—Daniel Harrison, Joel Lester, Eytan Agmon, Charles Smith, William Caplin, and Gregory Proctor, to name a few—have so many different nuanced understandings of function that it is nearly impossible for conversations on the subject to be completely understood by all parties. This is because function comprises at least four distinct aspects, which, when all called by the same name, function , create ambiguity, confusion, and contradiction. Part I of the dissertation first illuminates this ambiguity in the term function by giving a historical basis for four different aspects of function, three of which are traced to Riemann, and one of which is traced all the way back to Rameau. A solution to the problem of ambiguity is then proposed: the elimination of the term function . In place of function , four new terms—behavior , kinship , province , and quality —are invoked, each uniquely corresponding to one of the four aspects of function identified.
    [Show full text]
  • Invariance of Controller Fingerings Across a Continuum of Tunings
    Invariance of Controller Fingerings across a Continuum of Tunings Andrew Milne∗∗, William Setharesyy, and James Plamondonzz May 26, 2007 Introduction On the standard piano-style keyboard, intervals and chords have different shapes in each key. For example, the geometric pattern of the major third C–E is different from the geometric pattern of the major third D–F]. Similarly, the major scale is fingered differently in each of the twelve keys (in this usage, fingerings are specified without regard to which digits of the hand press which keys). Other playing surfaces, such as the keyboards of [Bosanquet, 1877] and [Wicki, 1896], have the property that each interval, chord, and scale type have the same geometric shape in every key. Such keyboards are said to be transpositionally invariant [Keisler, 1988]. There are many possible ways to tune musical intervals and scales, and the introduction of computer and software synthesizers makes it possible to realize any sound in any tuning [Carlos, 1987]. Typically, however, keyboard controllers are designed to play in a single tuning, such as the familiar 12-tone equal temperament (12-TET) which divides the octave into twelve perceptually equal pieces. Is it possible to create a keyboard surface that is capable of supporting many possible tunings? Is it possible to do so in a way that analogous musical intervals are fingered the same throughout the various tunings, so that (for example) the 12-TET fifth is fingered the same as the Just fifth and as the 17-TET fifth? (Just tunings ∗∗Corresponding author. Email: [email protected] yyDepartment of Electrical and Computer Engineering, University of Wisconsin-Madison, Madison, WI 53706 USA.
    [Show full text]
  • Invariant Fingering Over a Tuning Continuum
    Open Research Online The Open University’s repository of research publications and other research outputs Isomorphic controllers and Dynamic Tuning: invariant fingering over a tuning continuum Journal Item How to cite: Milne, Andrew; Sethares, William and Plamondon, James (2007). Isomorphic controllers and Dynamic Tuning: invariant fingering over a tuning continuum. Computer Music Journal, 31(4) pp. 15–32. For guidance on citations see FAQs. c 2007 Massachusetts Institute of Technology Version: Version of Record Link(s) to article on publisher’s website: http://dx.doi.org/doi:10.1162/comj.2007.31.4.15 http://www.mitpressjournals.org/loi/comj Copyright and Moral Rights for the articles on this site are retained by the individual authors and/or other copyright owners. For more information on Open Research Online’s data policy on reuse of materials please consult the policies page. oro.open.ac.uk Andrew Milne,* William Sethares,** and James Isomorphic Controllers and Plamondon† *Department of Music Dynamic Tuning: Invariant University of Jyväskylä Finland Fingering over a Tuning [email protected] **Department of Electrical and Computer Engineering Continuum University of Wisconsin-Madison Madison, WI 53706 USA [email protected] †Thumtronics Inc. 6911 Thistle Hill Way Austin, TX 78754 USA [email protected] In the Western musical tradition, two pitches are all within the time-honored framework of tonality. generally considered the “same” if they have nearly Such novel musical effects are discussed briefly in equal fundamental frequencies. Likewise, two the section on dynamic tuning, but the bulk of this pitches are in the “same” pitch class if the frequency article deals with the mathematical and perceptual of one is a power-of-two multiple of the other.
    [Show full text]