DOCSLIB.ORG

The Arithmetical Hierarchy in the Setting of 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Arithmetical Hierarchy in the Setting of 1 !1 - computability Arithmetical Hierarchy in !1 Computable infinitary formulas The Arithmetical Hierarchy in the Setting of !1 - Computability Jesse Johnson Department of Mathematics University of Notre Dame 2011 ASL North American Meeting – March 26, 2011 Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability !1 - computability Arithmetical Hierarchy in !1 Computable infinitary formulas A.H. in !1 - computability Joint work with Jacob Carson, Julia Knight, Karen Lange, Charles McCoy, John Wallbaum. The Arithmetical hierarchy in the setting of !1 - computability, preprint. Continuation of work from N. Greenberg and J. F. Knight, Computable structure theory in the setting of !1. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Introductory definitions Arithmetical Hierarchy in ! 1 Indicies and the jump Computable infinitary formulas Two definitions for the arithmetical hierarchy We will give two definitions for the arithmetical hierarchy in the setting of !1 - computability. The first will resemble the definition of the effective Borel Hierarchy. The second will resemble the standard definition of the hyper-arithmetical hierarchy. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Introductory definitions Arithmetical Hierarchy in ! 1 Indicies and the jump Computable infinitary formulas !1 - computability Definition Suppose R is a relation of countable arity α. R is computably enumerable if the set of ordinal codes for sequences in R is definable by a Σ1 formula in (L!1 ; ∈). R is computable if it is both c.e. and co-c.e. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Introductory definitions Arithmetical Hierarchy in ! 1 Indicies and the jump Computable infinitary formulas Working in !1 We assume that P(!) ⊆ L!1 . Results of Gödel give a computable 1-1 function g from the countable ordinals onto L!1 , such that the relation g(α) ∈ g(β) is computable. So, computing in !1 is essentially the same as computing in L!1 . Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Introductory definitions Arithmetical Hierarchy in ! 1 Indicies and the jump Computable infinitary formulas Indices for c.e. sets As in the standard setting, we have a c.e. set of codes for Σ1 definitions. We write Wα for the c.e. set with index α. All these definitions relativize in the natural way. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Introductory definitions Arithmetical Hierarchy in ! 1 Indicies and the jump Computable infinitary formulas The jump Definition We define the halting set as K = {α ∶ α ∈ Wα}. ′ X For a arbitrary set X, X = {α ∶ α ∈ Wα }. X(0) = X. X(α+1) = (X(α))′. For limit λ, X(λ) is the set of codes for pairs (β; x) such that β < λ and x ∈ X(β). 0 n−1 We write ∆n for ∅ for 1 ≤ n < !. 0 α We write ∆α for ∅ for α ≥ !. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Two definitions for the arithmetical hierarchy Arithmetical Hierarchy in ! 1 Comparing the two definitions Computable infinitary formulas First definition for the arithmetical hierarchy Our first definition of the arithmetical hierarchy resembles the definition of the effective Borel hierarchy. Definition Let R be a relation. 0 0 R is Σ0 and Π0 if it is computable. 0 0 R is Σ1 if it is c.e.; R is Π1 if the complementary relation, ¬ R, is c.e. 0 For countable α > 1, R is Σα if it is a c.e. union of relations, 0 0 0 each of which is Πβ for some β < α; R is Πα if ¬ R is Σα. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Two definitions for the arithmetical hierarchy Arithmetical Hierarchy in ! 1 Comparing the two definitions Computable infinitary formulas 0 0 Indices for Σα and Πα sets 0 0 For α ≥ 1, we may assign indices for the Σα and Πα sets in the natural way. For α = 1, we write (Σ; 1; γ) as the index for the c.e. set with index γ. The set with index (Π; 1; γ) is the complement. For α > 1, the set with index (Σ; α; γ) is the union of sets with indices in Wγ of the form (Π; β; δ) for some β < α and some countable δ. The set with index (Π; α; γ) is the complement. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Two definitions for the arithmetical hierarchy Arithmetical Hierarchy in ! 1 Comparing the two definitions Computable infinitary formulas Second definition for the arithmetical hierarchy Our second definition for the arithmetical hierarchy resembles the standard definition for the hyper-arithmetical hierarchy. Definition Let R be a relation. 0 0 R is Σ0 and Π0 if it is computable. 0 0 R is Σ1 if it is c.e.; R is Π1 if ¬ R, is c.e. 0 0 0 For α > 1, R is Σα if it is c.e. relative to ∆α; R is Πα if ¬ R 0 is Σα. 0 0 We assign indices for the Σα and Πα sets in the same way. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Two definitions for the arithmetical hierarchy Arithmetical Hierarchy in ! 1 Comparing the two definitions Computable infinitary formulas Comparing the two definitions The two definitions agree at finite levels, but disagree at level ! and beyond. Under the first definition, membership of an element into a 0 Σα set occurs if and only if that element is a member of 0 one of the lower Πβ sets. 0 So membership into a Σα set uses information from a single lower level. Under the second definition, membership of an element 0 0 into a Σα set may use a ∆α oracle to get information from all lower levels simultaneously. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Two definitions for the arithmetical hierarchy Arithmetical Hierarchy in ! 1 Comparing the two definitions Computable infinitary formulas The two definitions disagree at level ! Proposition 0 There is a set S that is ∆! under the second definition, but is 0 not Σ! under the first definition. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability ! - computability 1 Two definitions for the arithmetical hierarchy Arithmetical Hierarchy in ! 1 Comparing the two definitions Computable infinitary formulas Proof of the proposition Proof. Define S such that α ∈ S iff α is not in the set with index (Σ; !; α) under the first definition. 0 For each n, α, let Sα,n be the union of the Σn sets with indices in Wα of the form (Π; k; β) with k < n. The union of these sets over all n will be the set with index (Σ; !; α). 0 A ∆! oracle can determine whether α ∈ Sn,α for all n. So S 0 is ∆! under the second definition. 0 However, S cannot be one of the Σ! sets under the first defintion. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability !1 - computability Definitions Arithmetical Hierarchy in !1 Main theorem Computable infinitary formulas Conclusion Computable infinitary formulas The first definition of the computable infinitary formulas corresponds to the first definition of the arithmetical hierarchy. Definition Let L be a predicate language with computable symbols. We consider L-formulas '(x) with a countable tuple of variables x. '(x) is computable Σ0 and computable Π0 if it is a quantifier-free formula of L!1;!. For α > 0, '(x) is computable Σα if ' ≡ (∃u) i(u; x), c:e: where each i is computable Πβ for some β < α. '(x) is computable Πα if ' ≡ (∀u) i(u; x), where each c:e: i is computable Σβ for some β < α. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability !1 - computability Definitions Arithmetical Hierarchy in !1 Main theorem Computable infinitary formulas Conclusion Computable infinitary formulas The second definition of the computable infinitary formulas corresponds to the second definition of the arithmetical hierarchy. Definition '(x) is computable Σ0 and computable Π0 if it is a quantifier-free formula of L!1;!. For α > 0, '(x) is computable Σα if ' ≡ (∃u) i(u; x), c:e: where each i is a countable conjunction of formulas, each computable Πβ for some β < α. '(x) is computable Πα if ' ≡ (∀u) i(u; x), where each c:e: i is a countable disjunction of formulas, each computable Σβ for some β < α. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability !1 - computability Definitions Arithmetical Hierarchy in !1 Main theorem Computable infinitary formulas Conclusion Proposition on computable infinitary formulas Using either one of the definitions for the computable infinitary formulas, the following proposition holds and is proved by induction on α. Proposition Let A be an L-structure, and let '(x) be a computable Σα (computable Πα) L-formula. Then the relation defined by '(x) 0 0 in A is Σα (Πα) relative to A. Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability !1 - computability Definitions Arithmetical Hierarchy in !1 Main theorem Computable infinitary formulas Conclusion Relatively intrinsically arithmetical relations Definition Let A be a computable structure, and let R be a relation on A. 0 We say that R is relatively intrinsically Σα on A if for all 0 isomorphisms F from A onto a copy B, F(R) is Σα(B). Johnson The Arithmetical Hierarchy in the Setting of !1 - Computability !1 - computability Definitions Arithmetical Hierarchy in !1 Main theorem Computable infinitary formulas Conclusion Main theorem We now present our main theorem. Theorem Let 1 ≤ α < !1. For a relation R on a computable structure A, the following are equivalent: 1 0 R is relatively intrinsically Σα on A.
Load more

Recommended publications
  • The Polynomial Hierarchy
    ij 'I '""T', :J[_ ';(" THE POLYNOMIAL HIERARCHY Although the complexity classes we shall study now are in one sense byproducts of our definition of NP, they have a remarkable life of their own. 17.1 OPTIMIZATION PROBLEMS Optimization problems have not been classified in a satisfactory way within the theory of P and NP; it is these problems that motivate the immediate extensions of this theory beyond NP. Let us take the traveling salesman problem as our working example. In the problem TSP we are given the distance matrix of a set of cities; we want to find the shortest tour of the cities. We have studied the complexity of the TSP within the framework of P and NP only indirectly: We defined the decision version TSP (D), and proved it NP-complete (corollary to Theorem 9.7). For the purpose of understanding better the complexity of the traveling salesman problem, we now introduce two more variants. EXACT TSP: Given a distance matrix and an integer B, is the length of the shortest tour equal to B? Also, TSP COST: Given a distance matrix, compute the length of the shortest tour. The four variants can be ordered in "increasing complexity" as follows: TSP (D); EXACTTSP; TSP COST; TSP. Each problem in this progression can be reduced to the next. For the last three problems this is trivial; for the first two one has to notice that the reduction in 411 j ;1 17.1 Optimization Problems 413 I 412 Chapter 17: THE POLYNOMIALHIERARCHY the corollary to Theorem 9.7 proving that TSP (D) is NP-complete can be used with DP.
    [Show full text]
  • Complexity Theory
    Complexity Theory Course Notes Sebastiaan A. Terwijn Radboud University Nijmegen Department of Mathematics P.O. Box 9010 6500 GL Nijmegen the Netherlands [email protected] Copyright c 2010 by Sebastiaan A. Terwijn Version: December 2017 ii Contents 1 Introduction 1 1.1 Complexity theory . .1 1.2 Preliminaries . .1 1.3 Turing machines . .2 1.4 Big O and small o .........................3 1.5 Logic . .3 1.6 Number theory . .4 1.7 Exercises . .5 2 Basics 6 2.1 Time and space bounds . .6 2.2 Inclusions between classes . .7 2.3 Hierarchy theorems . .8 2.4 Central complexity classes . 10 2.5 Problems from logic, algebra, and graph theory . 11 2.6 The Immerman-Szelepcs´enyi Theorem . 12 2.7 Exercises . 14 3 Reductions and completeness 16 3.1 Many-one reductions . 16 3.2 NP-complete problems . 18 3.3 More decision problems from logic . 19 3.4 Completeness of Hamilton path and TSP . 22 3.5 Exercises . 24 4 Relativized computation and the polynomial hierarchy 27 4.1 Relativized computation . 27 4.2 The Polynomial Hierarchy . 28 4.3 Relativization . 31 4.4 Exercises . 32 iii 5 Diagonalization 34 5.1 The Halting Problem . 34 5.2 Intermediate sets . 34 5.3 Oracle separations . 36 5.4 Many-one versus Turing reductions . 38 5.5 Sparse sets . 38 5.6 The Gap Theorem . 40 5.7 The Speed-Up Theorem . 41 5.8 Exercises . 43 6 Randomized computation 45 6.1 Probabilistic classes . 45 6.2 More about BPP . 48 6.3 The classes RP and ZPP .
    [Show full text]
  • Syllabus Computability Theory
    Syllabus Computability Theory Sebastiaan A. Terwijn Institute for Discrete Mathematics and Geometry Technical University of Vienna Wiedner Hauptstrasse 8–10/E104 A-1040 Vienna, Austria [email protected] Copyright c 2004 by Sebastiaan A. Terwijn version: 2020 Cover picture and above close-up: Sunflower drawing by Alan Turing, c copyright by University of Southampton and King’s College Cambridge 2002, 2003. iii Emil Post (1897–1954) Alonzo Church (1903–1995) Kurt G¨odel (1906–1978) Stephen Cole Kleene Alan Turing (1912–1954) (1909–1994) Contents 1 Introduction 1 1.1 Preliminaries ................................ 2 2 Basic concepts 3 2.1 Algorithms ................................. 3 2.2 Recursion .................................. 4 2.2.1 Theprimitiverecursivefunctions . 4 2.2.2 Therecursivefunctions . 5 2.3 Turingmachines .............................. 6 2.4 Arithmetization............................... 10 2.4.1 Codingfunctions .......................... 10 2.4.2 Thenormalformtheorem . 11 2.4.3 The basic equivalence and Church’s thesis . 13 2.4.4 Canonicalcodingoffinitesets. 15 2.5 Exercises .................................. 15 3 Computable and computably enumerable sets 19 3.1 Diagonalization............................... 19 3.2 Computablyenumerablesets . 19 3.3 Undecidablesets .............................. 22 3.4 Uniformity ................................. 24 3.5 Many-onereducibility ........................... 25 3.6 Simplesets ................................. 26 3.7 Therecursiontheorem ........................... 28 3.8 Exercises
    [Show full text]
  • Logic and Complexity
    o| f\ Richard Lassaigne and Michel de Rougemont Logic and Complexity Springer Contents Introduction Part 1. Basic model theory and computability 3 Chapter 1. Prepositional logic 5 1.1. Propositional language 5 1.1.1. Construction of formulas 5 1.1.2. Proof by induction 7 1.1.3. Decomposition of a formula 7 1.2. Semantics 9 1.2.1. Tautologies. Equivalent formulas 10 1.2.2. Logical consequence 11 1.2.3. Value of a formula and substitution 11 1.2.4. Complete systems of connectives 15 1.3. Normal forms 15 1.3.1. Disjunctive and conjunctive normal forms 15 1.3.2. Functions associated to formulas 16 1.3.3. Transformation methods 17 1.3.4. Clausal form 19 1.3.5. OBDD: Ordered Binary Decision Diagrams 20 1.4. Exercises 23 Chapter 2. Deduction systems 25 2.1. Examples of tableaux 25 2.2. Tableaux method 27 2.2.1. Trees 28 2.2.2. Construction of tableaux 29 2.2.3. Development and closure 30 2.3. Completeness theorem 31 2.3.1. Provable formulas 31 2.3.2. Soundness 31 2.3.3. Completeness 32 2.4. Natural deduction 33 2.5. Compactness theorem 36 2.6. Exercices 38 vi CONTENTS Chapter 3. First-order logic 41 3.1. First-order languages 41 3.1.1. Construction of terms 42 3.1.2. Construction of formulas 43 3.1.3. Free and bound variables 44 3.2. Semantics 45 3.2.1. Structures and languages 45 3.2.2. Structures and satisfaction of formulas 46 3.2.3.
    [Show full text]
  • On the Weakness of Sharply Bounded Polynomial Induction
    On the Weakness of Sharply Bounded Polynomial Induction Jan Johannsen Friedrich-Alexander-Universit¨at Erlangen-N¨urnberg May 4, 1994 Abstract 0 We shall show that if the theory S2 of sharply bounded polynomial induction is extended 0 by symbols for certain functions and their defining axioms, it is still far weaker than T2 , which has ordinary sharply bounded induction. Furthermore, we show that this extended 0 b 0 system S2+ cannot Σ1-define every function in AC , the class of functions computable by polynomial size constant depth circuits. 1 Introduction i i The theory S2 of bounded arithmetic and its fragments S2 and T2 (i ≥ 0) were defined in [Bu]. The language of these theories comprises the usual language of arithmetic plus additional 1 |x|·|y| symbols for the functions ⌊ 2 x⌋, |x| := ⌈log2(x + 1)⌉ and x#y := 2 . Quantifiers of the form ∀x≤t , ∃x≤t are called bounded quantifiers. If the bounding term t is furthermore of the form b b |s|, the quantifier is called sharply bounded. The classes Σi and Πi of the bounded arithmetic hierarchy are defined in analogy to the classes of the usual arithmetical hierarchy, where the i counts alternations of bounded quantifiers, ignoring the sharply bounded quantifiers. i S2 is axiomatized by a finite set of open axioms (called BASIC) plus the schema of poly- b nomial induction (PIND) for Σi -formulae ϕ: 1 ϕ(0) ∧ ∀x ( ϕ(⌊ x⌋) → ϕ(x) ) → ∀x ϕ(x) 2 i b T2 is the same with the ordinary induction scheme for Σi -formulae replacing PIND.
    [Show full text]
  • An Introduction to Computability Theory
    AN INTRODUCTION TO COMPUTABILITY THEORY CINDY CHUNG Abstract. This paper will give an introduction to the fundamentals of com- putability theory. Based on Robert Soare's textbook, The Art of Turing Computability: Theory and Applications, we examine concepts including the Halting problem, properties of Turing jumps and degrees, and Post's Theo- rem.1 In the paper, we will assume the reader has a conceptual understanding of computer programs. Contents 1. Basic Computability 1 2. The Halting Problem 2 3. Post's Theorem: Jumps and Quantifiers 3 3.1. Arithmetical Hierarchy 3 3.2. Degrees and Jumps 4 3.3. The Zero-Jump, 00 5 3.4. Post's Theorem 5 Acknowledgments 8 References 8 1. Basic Computability Definition 1.1. An algorithm is a procedure capable of being carried out by a computer program. It accepts various forms of numerical inputs including numbers and finite strings of numbers. Computability theory is a branch of mathematical logic that focuses on algo- rithms, formally known in this area as computable functions, and studies the degree, or level of computability that can be attributed to various sets (these concepts will be formally defined and elaborated upon below). This field was founded in the 1930s by many mathematicians including the logicians: Alan Turing, Stephen Kleene, Alonzo Church, and Emil Post. Turing first pioneered computability theory when he introduced the fundamental concept of the a-machine which is now known as the Turing machine (this concept will be intuitively defined below) in his 1936 pa- per, On computable numbers, with an application to the Entscheidungsproblem[7].
    [Show full text]
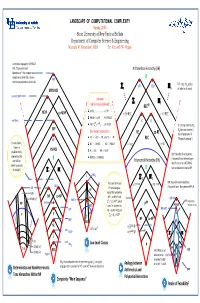
  • LANDSCAPE of COMPUTATIONAL COMPLEXITY Spring 2008 State University of New York at Buffalo Department of Computer Science & Engineering Mustafa M
    LANDSCAPE OF COMPUTATIONAL COMPLEXITY Spring 2008 State University of New York at Buffalo Department of Computer Science & Engineering Mustafa M. Faramawi, MBA Dr. Kenneth W. Regan A complete language for EXPSPACE: PIM, “Polynomial Ideal Arithmetical Hierarchy (AH) Membership”—the simplest natural completeness level that is known PIM not to have polynomial‐size circuits. TOT = {M : M is total, K(2) TOT e e ∑n Πn i.e. halts for all inputs} EXPSPACE Succinct 3SAT Unknown ∑2 Π2 but Commonly Believed: RECRE L ≠ NL …………………….. L ≠ PH NEXP co‐NEXP = ∃∀.REC = ∀∃.REC P ≠ NP ∩ co‐NP ……… P ≠ PSPACE nxn Chess p p K D NP ≠ ∑ 2 ∩Π 2 ……… NP ≠ EXP D = {Turing machines M : EXP e Best Known Separations: Me does not accept e} = RE co‐RE the complement of K. AC0 ⊂ ACC0 ⊂ PP, also TC0 ⊂ PP QBF REC (“Diagonal Language”) For any fixed k, NC1 ⊂ PSPACE, …, NL ⊂ PSPACE = ∃.REC = ∀.REC there is a PSPACE problem in this P ⊂ EXP, NP ⊂ NEXP BQP: Bounded‐Error Quantum intersection that PSPACE ⊂ EXPSPACE Polynomial Time. Believed larger can NOT be Polynomial Hierarchy (PH) than P since it has FACTORING, solved by circuits p p k but not believed to contain NP. of size O(n ) ∑ 2 Π 2 L WS5 p p ∑ 2 Π 2 The levels of AH and poly. poly. BPP: Bounded‐Error Probabilistic TAUT = ∃∀ P = ∀∃ P SAT Polynomial Time. Many believe BPP = P. NC1 PH are analogous, NLIN except that we believe NP co‐NP 0 NP ∩ co‐NP ≠ P and NTIME [n2] TC QBF PARITY ∑p ∩Πp NP PP Probabilistic NP FACT 2 2 ≠ P , which NP ACC0 stand in contrast to P PSPACE Polynomial Time MAJ‐SAT CVP RE ∩ co‐RE = REC and 0 AC RE P P ∑2 ∩Π2 = REC GAP NP co‐NP REG NL poly 0 0 ∃ .
    [Show full text]
  • Contributions to the Study of Resource-Bounded Measure
    Contributions to the Study of ResourceBounded Measure Elvira Mayordomo Camara Barcelona abril de Contributions to the Study of ResourceBounded Measure Tesis do ctoral presentada en el Departament de Llenguatges i Sistemes Informatics de la Universitat Politecnica de Catalunya para optar al grado de Do ctora en Ciencias Matematicas por Elvira Mayordomo Camara Dirigida p or el do ctor Jose Luis Balcazar Navarro Barcelona abril de This dissertation was presented on June st in the Departament de Llenguatges i Sistemes Informatics Universitat Politecnica de Catalunya The committee was formed by the following members Prof Ronald V Bo ok University of California at Santa Barbara Prof Ricard Gavalda Universitat Politecnica de Catalunya Prof Mario Ro drguez Universidad Complutense de Madrid Prof Marta Sanz Universitat Central de Barcelona Prof Jacob o Toran Universitat Politecnica de Catalunya Acknowledgements Iwant to thank sp ecially two p eople Jose Luis Balcazar and Jack Lutz Without their help and encouragement this dissertation would never have b een written Jose Luis Balcazar was my advisor and taughtmemostofwhatIknow ab out Structural Complexity showing me with his example how to do research I visited Jack Lutz in Iowa State University in several o ccasions from His patience and enthusiasm in explaining to me the intuition behind his theory and his numerous ideas were the starting p ointofmostoftheresults in this dissertation Several coauthors have collab orated in the publications included in the dierent chapters Jack Lutz Steven
    [Show full text]
  • On Infinite Variants of NP-Complete Problems
    Journal of Computer and System Sciences SS1432 journal of computer and system sciences 53, 180193 (1996) article no. 0060 View metadata, citation and similarTaking papers at core.ac.uk It to the Limit: On Infinite Variants brought to you by CORE of NP-Complete Problems provided by Elsevier - Publisher Connector Tirza Hirst and David Harel* Department of Applied Mathematics H Computer Science, The Weizmann Institute of Science, Rehovot 76100, Israel Received November 1, 1993 We first set up a general way of obtaining infinite versions We define infinite, recursive versions of NP optimization problems. of NP maximization and minimization problems. If P is the For example, MAX CLIQUE becomes the question of whether a recursive problem that asks for a maximum by graph contains an infinite clique. The present paper was motivated by trying to understand what makes some NP problems highly max |[wÄ : A<,(wÄ , S)]|, undecidable in the infinite case, while others remain on low levels of S the arithmetical hierarchy. We prove two results; one enables using knowledge about the infinite case to yield implications to the finite where ,(wÄ , S) is first-order and A is a finite structure (say, case, and the other enables implications in the other direction. a graph), we define P as the problem that asks whether Moreover, taken together, the two results provide a method for proving there is an S, such that the set [wÄ : A<,(w, S)] is infinite, (finitary) problems to be outside the syntactic class MAX NP, and, where A is an infinite recursive structure. Thus, for example, hence, outside MAX SNP too, by showing that their infinite versions are 1 Max Clique becomes the question of whether a recursive 71-complete.
    [Show full text]
  • Computational Complexity: a Modern Approach PDF Book
    COMPUTATIONAL COMPLEXITY: A MODERN APPROACH PDF, EPUB, EBOOK Sanjeev Arora,Boaz Barak | 594 pages | 16 Jun 2009 | CAMBRIDGE UNIVERSITY PRESS | 9780521424264 | English | Cambridge, United Kingdom Computational Complexity: A Modern Approach PDF Book Miller; J. The polynomial hierarchy and alternations; 6. This is a very comprehensive and detailed book on computational complexity. Circuit lower bounds; Examples and solved exercises accompany key definitions. Computational complexity: A conceptual perspective. Redirected from Computational complexities. Refresh and try again. Brand new Book. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity , i. In other words, one considers that the computation is done simultaneously on as many identical processors as needed, and the non-deterministic computation time is the time spent by the first processor that finishes the computation. Foundations of Cryptography by Oded Goldreich - Cambridge University Press The book gives the mathematical underpinnings for cryptography; this includes one-way functions, pseudorandom generators, and zero-knowledge proofs. If one knows an upper bound on the size of the binary representation of the numbers that occur during a computation, the time complexity is generally the product of the arithmetic complexity by a constant factor. Jason rated it it was amazing Aug 28, Seller Inventory bc0bebcaa63d3c. Lewis Cawthorne rated it really liked it Dec 23, Polynomial hierarchy Exponential hierarchy Grzegorczyk hierarchy Arithmetical hierarchy Boolean hierarchy. Convert currency. Convert currency. Familiarity with discrete mathematics and probability will be assumed. The formal language associated with this decision problem is then the set of all connected graphs — to obtain a precise definition of this language, one has to decide how graphs are encoded as binary strings.
    [Show full text]
  • Computability Theory of Hyperarithmetical Sets
    WESTFALISCHE¨ WILHELMS-UNIVERSITAT¨ MUNSTER¨ INSTITUT FUR¨ MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG Computability Theory of Hyperarithmetical Sets Lecture by Wolfram Pohlers Summer–Term 1996 Typeset by Martina Pfeifer Preface This text contains the somewhat extended material of a series of lectures given at the University of M¨unster. The aim of the course is to give an introduction to “higher” computability theory and to provide background material for the following courses in proof theory. The prerequisites for the course are some basic facts about computable functions and mathe- matical logic. Some emphasis has been put on the notion of generalized inductive definitions. Whenever it seemed to be opportune we tried to obtain “classical” results by using generalized inductive definitions. I am indebted to Dipl. Math. INGO LEPPER for the revising and supplementing the original text. M¨unster, September 1999 WOLFRAM POHLERS 2 Contents Contents 1 Computable Functionals and Relations ....................... 5 1.1FunctionalsandRelations................................ 5 1.2TheNormal–formTheorem............................... 10 1.3 Computability relativized . ............................... 13 2 Degrees ......................................... 15 2.1 m–Degrees....................................... 15 2.2 TURING–Reducibility . ............................... 16 2.3 TURING–Degrees.................................... 18 3 The Arithmetical Hierarchy ............................. 25 3.1TheJumpoperatorrevisited.............................. 25
    [Show full text]
  • Arithmetical Hierarchy
    Arithmetical Hierarchy Klaus Sutner Carnegie Mellon University 60-arith-hier 2017/12/15 23:18 1 The Turing Jump Arithmetical Hierarchy Definability Formal Systems Recall: Oracles 3 We can attach an orcale to a Turing machine without changing the basic theory. fegA eth function computable with A A A We = domfeg eth r.e. set with A The constructions are verbatim the same. For example, a universal Turing machine turns into a universal Turing machine plus oracle. The Use Principle 4 We continue to confuse a set A ⊆ N with its characteristic function. For any n write A n for the following finite approximation to the characteristic function: ( A(z) if z < n, (A n)(z) ' " otherwise. For any such function α write α < A if α = A n for some n. Then fegA(x) = y () 9 α < A fegα(x) = y with the understanding that the computation on the right never asks the oracle any questions outside of its domain. Of course, a divergent computation may use the oracle infinitely often. Generalized Halting 5 Definition Let A ⊆ N. The (Turing) jump of A is defined as A0 = KA = f e j fegA(e) # g So ;0 = K; = K is just the ordinary Halting set. The nth jump A(n) is obtained by iterating the jump n times. Jump Properties 6 Let A; B ⊆ N. Theorem A0 is r.e. in A. A0 is not Turing reducible to A. 0 B is r.e. in A iff B ≤m A . Proof. The first two parts are verbatim re-runs of the oracle-free argument.
    [Show full text]