DOCSLIB.ORG

Contributions to the Study of Resource-Bounded Measure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Contributions to the Study of Resource-Bounded Measure Contributions to the Study of ResourceBounded Measure Elvira Mayordomo Camara Barcelona abril de Contributions to the Study of ResourceBounded Measure Tesis do ctoral presentada en el Departament de Llenguatges i Sistemes Informatics de la Universitat Politecnica de Catalunya para optar al grado de Do ctora en Ciencias Matematicas por Elvira Mayordomo Camara Dirigida p or el do ctor Jose Luis Balcazar Navarro Barcelona abril de This dissertation was presented on June st in the Departament de Llenguatges i Sistemes Informatics Universitat Politecnica de Catalunya The committee was formed by the following members Prof Ronald V Bo ok University of California at Santa Barbara Prof Ricard Gavalda Universitat Politecnica de Catalunya Prof Mario Ro drguez Universidad Complutense de Madrid Prof Marta Sanz Universitat Central de Barcelona Prof Jacob o Toran Universitat Politecnica de Catalunya Acknowledgements Iwant to thank sp ecially two p eople Jose Luis Balcazar and Jack Lutz Without their help and encouragement this dissertation would never have b een written Jose Luis Balcazar was my advisor and taughtmemostofwhatIknow ab out Structural Complexity showing me with his example how to do research I visited Jack Lutz in Iowa State University in several o ccasions from His patience and enthusiasm in explaining to me the intuition behind his theory and his numerous ideas were the starting p ointofmostoftheresults in this dissertation Several coauthors have collab orated in the publications included in the dierent chapters Jack Lutz Steven Fenner Ronald Bo ok Jose Luis Balcazar Monsterrat Hermo and Harry Buhrman In addition a number of other p eople have contributed with dierent ideas among others Peter Miltersen Eric Allender and Martin Strauss Thanks to all the p eople that help ed me during my visits to Iowa State University the University of Ulm the University of California at Santa Barbara and the University of Aarhus I sp ecially appreciate the hospitalityof Robyn Lutz and Celia Wrathall The Spanish Ministerio de Educacion y Ciencia supp orted this work through grant FPI PN I received partial supp ort from Accion Integrada HA by the ESPRIT EC pro ject ALCOM and by National Science Foundation Grant CCR The p eople in the Department de Llenguatges i Sistemes Informatics have given me their friendship and help through these years In the section of Theoretical Computer Science I found lots of interesting discussions and p eople that listened to my often still incoherent ideas FinallyI thank my family for b eing there And Juanjo for his love and supp ort Contents Intro duction and preliminaries Intro duction Main contributions Preliminaries Resourceb ounded measure Some technical lemmas measurability and the Kolmogorov law Measuring in PSPACE Intro duction Measure in PSPACE additivity in PSPACE Measure versus category the Pbiimmune sets Intro duction Pbiimmunity and resourceb ounded measure Pbiimmunity and resourceb ounded category Measure of nonuniform complexity classes Intro duction Advice complexity classes Weaksto chasticity c Measure of P DENSE n tt Pp oly inside the Exp onential Hierarchy If NP is not small Intro duction If NP do es not have pmeasure Separating completeness notions in NP Separating reducibilities in NP Further results and op en problems Cones Intro duction Weaklyuseful languages On the robustness of ALMOSTR Bidimensional measure References Chapter Intro duction and preliminaries Intro duction The notion of eective pro cedure or algorithm was b orn in the early thirties building on the work of Church Godel Kleene Post and Turing Chur Chur Gode Klee Post Turi Turi They develop ed several formalizations of this concept such as calculus partial recursive functions and the Turing Machine formalism This was the base of Recursive Function Theory where recursive problems were dened as those that are solvable by an algorithm The construction of actual computers led to the consideration of feasibly solvable prob lems instead of recursive or theoretically solvable ones This distinction was related to the explosive growth of the exp onential function which implies that algorithms based on exhaustive searchmay b e infeasible in practice Therefore an increasing attention was paid in the sixties to the amount of computational resources used in the solution of a recursive problem Sp ecically the resources considered were mainly time and space With the work of Hartmanis Stearns and Lewis HartSt LewiStH SteaHaL Com plexity Theory started a division of recursive problems into complexity classes according to the amount of resources used in their resolution The computing mo del used here was the Turing Machine which corresp onds to a simple mathematical representation of a computer see Hop cUl for a complete description The problems that can be solved in time p olynomial in the length of the input are considered feasibly solvable and form the class denoted P But there exist many problems for which no p olynomial time algorithm is known many imp ortant ones among them have the prop erty of b eing easy to check that is once a solution is found it can be checked in p olynomial time that it is indeed a solution This leads to the denition of the class NP as the class of easytocheck prob lems there are many imp ortant problems in this class for instance those dealing with the satisfability of b o olean formulas or with the existence of a hamiltonian path in a graph and some practical op eration research problems such as the distribution of crews into planes It would be very interesting to know whether P and NP coincide In the seventies some techniques analogous to those in Recursive Function Theory for instance the concept of completeness Co ok Karp started to be develop ed and then used to attack the P NP problem This constitutes the b eginning of the eld of Structural Complexity versus which we develop next Structural Complexity describ es complexity classes using various typ es of resources in cluding time space nondeterministic time and space Bo olean circuit size and depth and alternating time and space We will not dene here all the mentioned resources let us just say that the word nondeterministic refers to the use of nondeterministic algorithms that INTRODUCTION are a generalization of the usual algorithms with the extra p ossibility of cho osing among several instructions that follow a given one and that the word alternating is indirectly related to the use of parallel algorithms in which several instructions can be run at the same time The problems considered are mainly decisional ones which are denoted as languages and we say that an algorithm recognizes a language when it solves the cor resp onding decisional problem The main op en problems in Structural Complexity have the form Is the class of languages that can be recognized with an amount f of resource included in the class of those recognized with an amount g of resource The ab ove mentioned P versus NP problem can b e formulated as Is the class of languages that can b e recognized with nondeterministic p olynomial time included in the class of the p olynomial time recognizable languages Other examples involve comparisons of p olynomial time P versus p olylogarithmic parallel time with p olynomial size hardware NC exp onential time E versus p olynomial size circuits Pp oly and p olynomial space PSPACE versus p olynomial time P The notions of oracle Turing Machine reduction and complete language are intro duced in order to compare the complexity of sp ecic languages An oracle Turing Machine is an ordinary Turing Machine equipp ed with direct access to a particular language A which is called oracle The oracle Turing Machine op erates as an ordinary one with the extra p ossibility of given a string q computing in a single step the answer to q A For each oracle A we can dene complexity classes according to the resources used to recognize a language when we can access oracle A This means that for each oracle A we have a particular computation universe where the solution of A is given for free A great eort was done to nd out which answers to op en problems of the form C D hold when translated into some such universe trying to get some light on the solution of the op en problem see BakeGiS for the rst work in this line Given a problem such as C D we say that it is nonrelativizable when there exist oracles A and B such that C D using oracle A and C D using oracle B that is the solution of the problem is dierent in the contexts of oracles A and B A nonrelativizable problem is considered dicult because most of the techniques used in Structural Complexity are indep endent of the oracle used Just a few new results have shown that nonrelativizable problems are not imp ossible to solve for instance Shamir has shown in Sham that PSPACE IP while there exist oracles for which the opp osite holds FortSi If we can recognize a language A with an oracle B this means that B is at least as hard to recognize as A since an algorithm for B would pro duce an algorithm for A This denes a partial preorder of languages denoted and called Turing reducibility with the meaning T that A B if A can be recognized using B as oracle Polynomial time reducibilities T app ear when considering
Load more

Recommended publications
  • The Complexity Zoo
    The Complexity Zoo Scott Aaronson www.ScottAaronson.com LATEX Translation by Chris Bourke [email protected] 417 classes and counting 1 Contents 1 About This Document 3 2 Introductory Essay 4 2.1 Recommended Further Reading ......................... 4 2.2 Other Theory Compendia ............................ 5 2.3 Errors? ....................................... 5 3 Pronunciation Guide 6 4 Complexity Classes 10 5 Special Zoo Exhibit: Classes of Quantum States and Probability Distribu- tions 110 6 Acknowledgements 116 7 Bibliography 117 2 1 About This Document What is this? Well its a PDF version of the website www.ComplexityZoo.com typeset in LATEX using the complexity package. Well, what’s that? The original Complexity Zoo is a website created by Scott Aaronson which contains a (more or less) comprehensive list of Complexity Classes studied in the area of theoretical computer science known as Computa- tional Complexity. I took on the (mostly painless, thank god for regular expressions) task of translating the Zoo’s HTML code to LATEX for two reasons. First, as a regular Zoo patron, I thought, “what better way to honor such an endeavor than to spruce up the cages a bit and typeset them all in beautiful LATEX.” Second, I thought it would be a perfect project to develop complexity, a LATEX pack- age I’ve created that defines commands to typeset (almost) all of the complexity classes you’ll find here (along with some handy options that allow you to conveniently change the fonts with a single option parameters). To get the package, visit my own home page at http://www.cse.unl.edu/~cbourke/.
    [Show full text]
  • The Polynomial Hierarchy
    ij 'I '""T', :J[_ ';(" THE POLYNOMIAL HIERARCHY Although the complexity classes we shall study now are in one sense byproducts of our definition of NP, they have a remarkable life of their own. 17.1 OPTIMIZATION PROBLEMS Optimization problems have not been classified in a satisfactory way within the theory of P and NP; it is these problems that motivate the immediate extensions of this theory beyond NP. Let us take the traveling salesman problem as our working example. In the problem TSP we are given the distance matrix of a set of cities; we want to find the shortest tour of the cities. We have studied the complexity of the TSP within the framework of P and NP only indirectly: We defined the decision version TSP (D), and proved it NP-complete (corollary to Theorem 9.7). For the purpose of understanding better the complexity of the traveling salesman problem, we now introduce two more variants. EXACT TSP: Given a distance matrix and an integer B, is the length of the shortest tour equal to B? Also, TSP COST: Given a distance matrix, compute the length of the shortest tour. The four variants can be ordered in "increasing complexity" as follows: TSP (D); EXACTTSP; TSP COST; TSP. Each problem in this progression can be reduced to the next. For the last three problems this is trivial; for the first two one has to notice that the reduction in 411 j ;1 17.1 Optimization Problems 413 I 412 Chapter 17: THE POLYNOMIALHIERARCHY the corollary to Theorem 9.7 proving that TSP (D) is NP-complete can be used with DP.
    [Show full text]
  • Complexity Theory
    Complexity Theory Course Notes Sebastiaan A. Terwijn Radboud University Nijmegen Department of Mathematics P.O. Box 9010 6500 GL Nijmegen the Netherlands [email protected] Copyright c 2010 by Sebastiaan A. Terwijn Version: December 2017 ii Contents 1 Introduction 1 1.1 Complexity theory . .1 1.2 Preliminaries . .1 1.3 Turing machines . .2 1.4 Big O and small o .........................3 1.5 Logic . .3 1.6 Number theory . .4 1.7 Exercises . .5 2 Basics 6 2.1 Time and space bounds . .6 2.2 Inclusions between classes . .7 2.3 Hierarchy theorems . .8 2.4 Central complexity classes . 10 2.5 Problems from logic, algebra, and graph theory . 11 2.6 The Immerman-Szelepcs´enyi Theorem . 12 2.7 Exercises . 14 3 Reductions and completeness 16 3.1 Many-one reductions . 16 3.2 NP-complete problems . 18 3.3 More decision problems from logic . 19 3.4 Completeness of Hamilton path and TSP . 22 3.5 Exercises . 24 4 Relativized computation and the polynomial hierarchy 27 4.1 Relativized computation . 27 4.2 The Polynomial Hierarchy . 28 4.3 Relativization . 31 4.4 Exercises . 32 iii 5 Diagonalization 34 5.1 The Halting Problem . 34 5.2 Intermediate sets . 34 5.3 Oracle separations . 36 5.4 Many-one versus Turing reductions . 38 5.5 Sparse sets . 38 5.6 The Gap Theorem . 40 5.7 The Speed-Up Theorem . 41 5.8 Exercises . 43 6 Randomized computation 45 6.1 Probabilistic classes . 45 6.2 More about BPP . 48 6.3 The classes RP and ZPP .
    [Show full text]
  • Axiomatizing Resource Bounds for Measure
    Axiomatizing Resource Bounds for Measure ⋆ Xiaoyang Gu1 ⋆⋆, Jack H. Lutz2 ⋆ ⋆ ⋆, Satyadev Nandakumar3, and James S. Royer4 † 1 LinkedIn Corporation, Mountain View, CA 94043, U. S. A. [email protected] 2 Iowa State University Ames, IA 50011, U. S. A. [email protected] 3 I. I. T. Kanpur Kanpur, UP 280 016 India. [email protected] 4 Syracuse University Syracuse, New York 13244, U. S. A. [email protected] Abstract. Resource-bounded measure is a generalization of classical Lebesgue measure that is useful in computational complexity. The central parameter of resource-bounded measure is the resource bound ∆, which is a class of functions. When ∆ is unrestricted, i.e., contains all functions with the specified domains and codomains, resource-bounded measure coincides with classical Lebesgue measure. On the other hand, when ∆ contains functions satisfying some complexity constraint, resource-bounded measure imposes internal measure structure on a corresponding complexity class. Most applications of resource-bounded measure use only the “measure-zero/measure-one fragment” of the theory. For this fragment, ∆ can be taken to be a class of type-one functions (e.g., from strings to rationals). However, in the full theory of resource-bounded measurability and measure, the resource bound ∆ also contains type-two functionals. To date, both the full theory and its zero-one fragment have been developed in terms of a list of example resource bounds chosen for their apparent utility. This paper replaces this list-of-examples approach with a careful investigation of the conditions that suffice for a class ∆ to be a resource bound.
    [Show full text]
  • Glossary of Complexity Classes
    App endix A Glossary of Complexity Classes Summary This glossary includes selfcontained denitions of most complexity classes mentioned in the b o ok Needless to say the glossary oers a very minimal discussion of these classes and the reader is re ferred to the main text for further discussion The items are organized by topics rather than by alphab etic order Sp ecically the glossary is partitioned into two parts dealing separately with complexity classes that are dened in terms of algorithms and their resources ie time and space complexity of Turing machines and complexity classes de ned in terms of nonuniform circuits and referring to their size and depth The algorithmic classes include timecomplexity based classes such as P NP coNP BPP RP coRP PH E EXP and NEXP and the space complexity classes L NL RL and P S P AC E The non k uniform classes include the circuit classes P p oly as well as NC and k AC Denitions and basic results regarding many other complexity classes are available at the constantly evolving Complexity Zoo A Preliminaries Complexity classes are sets of computational problems where each class contains problems that can b e solved with sp ecic computational resources To dene a complexity class one sp ecies a mo del of computation a complexity measure like time or space which is always measured as a function of the input length and a b ound on the complexity of problems in the class We follow the tradition of fo cusing on decision problems but refer to these problems using the terminology of promise problems
    [Show full text]
  • Syllabus Computability Theory
    Syllabus Computability Theory Sebastiaan A. Terwijn Institute for Discrete Mathematics and Geometry Technical University of Vienna Wiedner Hauptstrasse 8–10/E104 A-1040 Vienna, Austria [email protected] Copyright c 2004 by Sebastiaan A. Terwijn version: 2020 Cover picture and above close-up: Sunflower drawing by Alan Turing, c copyright by University of Southampton and King’s College Cambridge 2002, 2003. iii Emil Post (1897–1954) Alonzo Church (1903–1995) Kurt G¨odel (1906–1978) Stephen Cole Kleene Alan Turing (1912–1954) (1909–1994) Contents 1 Introduction 1 1.1 Preliminaries ................................ 2 2 Basic concepts 3 2.1 Algorithms ................................. 3 2.2 Recursion .................................. 4 2.2.1 Theprimitiverecursivefunctions . 4 2.2.2 Therecursivefunctions . 5 2.3 Turingmachines .............................. 6 2.4 Arithmetization............................... 10 2.4.1 Codingfunctions .......................... 10 2.4.2 Thenormalformtheorem . 11 2.4.3 The basic equivalence and Church’s thesis . 13 2.4.4 Canonicalcodingoffinitesets. 15 2.5 Exercises .................................. 15 3 Computable and computably enumerable sets 19 3.1 Diagonalization............................... 19 3.2 Computablyenumerablesets . 19 3.3 Undecidablesets .............................. 22 3.4 Uniformity ................................. 24 3.5 Many-onereducibility ........................... 25 3.6 Simplesets ................................. 26 3.7 Therecursiontheorem ........................... 28 3.8 Exercises
    [Show full text]
  • Quantum Computational Complexity Theory Is to Un- Derstand the Implications of Quantum Physics to Computational Complexity Theory
    Quantum Computational Complexity John Watrous Institute for Quantum Computing and School of Computer Science University of Waterloo, Waterloo, Ontario, Canada. Article outline I. Definition of the subject and its importance II. Introduction III. The quantum circuit model IV. Polynomial-time quantum computations V. Quantum proofs VI. Quantum interactive proof systems VII. Other selected notions in quantum complexity VIII. Future directions IX. References Glossary Quantum circuit. A quantum circuit is an acyclic network of quantum gates connected by wires: the gates represent quantum operations and the wires represent the qubits on which these operations are performed. The quantum circuit model is the most commonly studied model of quantum computation. Quantum complexity class. A quantum complexity class is a collection of computational problems that are solvable by a cho- sen quantum computational model that obeys certain resource constraints. For example, BQP is the quantum complexity class of all decision problems that can be solved in polynomial time by a arXiv:0804.3401v1 [quant-ph] 21 Apr 2008 quantum computer. Quantum proof. A quantum proof is a quantum state that plays the role of a witness or certificate to a quan- tum computer that runs a verification procedure. The quantum complexity class QMA is defined by this notion: it includes all decision problems whose yes-instances are efficiently verifiable by means of quantum proofs. Quantum interactive proof system. A quantum interactive proof system is an interaction between a verifier and one or more provers, involving the processing and exchange of quantum information, whereby the provers attempt to convince the verifier of the answer to some computational problem.
    [Show full text]
  • Logic and Complexity
    o| f\ Richard Lassaigne and Michel de Rougemont Logic and Complexity Springer Contents Introduction Part 1. Basic model theory and computability 3 Chapter 1. Prepositional logic 5 1.1. Propositional language 5 1.1.1. Construction of formulas 5 1.1.2. Proof by induction 7 1.1.3. Decomposition of a formula 7 1.2. Semantics 9 1.2.1. Tautologies. Equivalent formulas 10 1.2.2. Logical consequence 11 1.2.3. Value of a formula and substitution 11 1.2.4. Complete systems of connectives 15 1.3. Normal forms 15 1.3.1. Disjunctive and conjunctive normal forms 15 1.3.2. Functions associated to formulas 16 1.3.3. Transformation methods 17 1.3.4. Clausal form 19 1.3.5. OBDD: Ordered Binary Decision Diagrams 20 1.4. Exercises 23 Chapter 2. Deduction systems 25 2.1. Examples of tableaux 25 2.2. Tableaux method 27 2.2.1. Trees 28 2.2.2. Construction of tableaux 29 2.2.3. Development and closure 30 2.3. Completeness theorem 31 2.3.1. Provable formulas 31 2.3.2. Soundness 31 2.3.3. Completeness 32 2.4. Natural deduction 33 2.5. Compactness theorem 36 2.6. Exercices 38 vi CONTENTS Chapter 3. First-order logic 41 3.1. First-order languages 41 3.1.1. Construction of terms 42 3.1.2. Construction of formulas 43 3.1.3. Free and bound variables 44 3.2. Semantics 45 3.2.1. Structures and languages 45 3.2.2. Structures and satisfaction of formulas 46 3.2.3.
    [Show full text]
  • On the Weakness of Sharply Bounded Polynomial Induction
    On the Weakness of Sharply Bounded Polynomial Induction Jan Johannsen Friedrich-Alexander-Universit¨at Erlangen-N¨urnberg May 4, 1994 Abstract 0 We shall show that if the theory S2 of sharply bounded polynomial induction is extended 0 by symbols for certain functions and their defining axioms, it is still far weaker than T2 , which has ordinary sharply bounded induction. Furthermore, we show that this extended 0 b 0 system S2+ cannot Σ1-define every function in AC , the class of functions computable by polynomial size constant depth circuits. 1 Introduction i i The theory S2 of bounded arithmetic and its fragments S2 and T2 (i ≥ 0) were defined in [Bu]. The language of these theories comprises the usual language of arithmetic plus additional 1 |x|·|y| symbols for the functions ⌊ 2 x⌋, |x| := ⌈log2(x + 1)⌉ and x#y := 2 . Quantifiers of the form ∀x≤t , ∃x≤t are called bounded quantifiers. If the bounding term t is furthermore of the form b b |s|, the quantifier is called sharply bounded. The classes Σi and Πi of the bounded arithmetic hierarchy are defined in analogy to the classes of the usual arithmetical hierarchy, where the i counts alternations of bounded quantifiers, ignoring the sharply bounded quantifiers. i S2 is axiomatized by a finite set of open axioms (called BASIC) plus the schema of poly- b nomial induction (PIND) for Σi -formulae ϕ: 1 ϕ(0) ∧ ∀x ( ϕ(⌊ x⌋) → ϕ(x) ) → ∀x ϕ(x) 2 i b T2 is the same with the ordinary induction scheme for Σi -formulae replacing PIND.
    [Show full text]
  • An Introduction to Computability Theory
    AN INTRODUCTION TO COMPUTABILITY THEORY CINDY CHUNG Abstract. This paper will give an introduction to the fundamentals of com- putability theory. Based on Robert Soare's textbook, The Art of Turing Computability: Theory and Applications, we examine concepts including the Halting problem, properties of Turing jumps and degrees, and Post's Theo- rem.1 In the paper, we will assume the reader has a conceptual understanding of computer programs. Contents 1. Basic Computability 1 2. The Halting Problem 2 3. Post's Theorem: Jumps and Quantifiers 3 3.1. Arithmetical Hierarchy 3 3.2. Degrees and Jumps 4 3.3. The Zero-Jump, 00 5 3.4. Post's Theorem 5 Acknowledgments 8 References 8 1. Basic Computability Definition 1.1. An algorithm is a procedure capable of being carried out by a computer program. It accepts various forms of numerical inputs including numbers and finite strings of numbers. Computability theory is a branch of mathematical logic that focuses on algo- rithms, formally known in this area as computable functions, and studies the degree, or level of computability that can be attributed to various sets (these concepts will be formally defined and elaborated upon below). This field was founded in the 1930s by many mathematicians including the logicians: Alan Turing, Stephen Kleene, Alonzo Church, and Emil Post. Turing first pioneered computability theory when he introduced the fundamental concept of the a-machine which is now known as the Turing machine (this concept will be intuitively defined below) in his 1936 pa- per, On computable numbers, with an application to the Entscheidungsproblem[7].
    [Show full text]
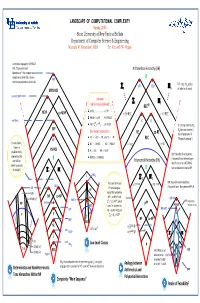
  • LANDSCAPE of COMPUTATIONAL COMPLEXITY Spring 2008 State University of New York at Buffalo Department of Computer Science & Engineering Mustafa M
    LANDSCAPE OF COMPUTATIONAL COMPLEXITY Spring 2008 State University of New York at Buffalo Department of Computer Science & Engineering Mustafa M. Faramawi, MBA Dr. Kenneth W. Regan A complete language for EXPSPACE: PIM, “Polynomial Ideal Arithmetical Hierarchy (AH) Membership”—the simplest natural completeness level that is known PIM not to have polynomial‐size circuits. TOT = {M : M is total, K(2) TOT e e ∑n Πn i.e. halts for all inputs} EXPSPACE Succinct 3SAT Unknown ∑2 Π2 but Commonly Believed: RECRE L ≠ NL …………………….. L ≠ PH NEXP co‐NEXP = ∃∀.REC = ∀∃.REC P ≠ NP ∩ co‐NP ……… P ≠ PSPACE nxn Chess p p K D NP ≠ ∑ 2 ∩Π 2 ……… NP ≠ EXP D = {Turing machines M : EXP e Best Known Separations: Me does not accept e} = RE co‐RE the complement of K. AC0 ⊂ ACC0 ⊂ PP, also TC0 ⊂ PP QBF REC (“Diagonal Language”) For any fixed k, NC1 ⊂ PSPACE, …, NL ⊂ PSPACE = ∃.REC = ∀.REC there is a PSPACE problem in this P ⊂ EXP, NP ⊂ NEXP BQP: Bounded‐Error Quantum intersection that PSPACE ⊂ EXPSPACE Polynomial Time. Believed larger can NOT be Polynomial Hierarchy (PH) than P since it has FACTORING, solved by circuits p p k but not believed to contain NP. of size O(n ) ∑ 2 Π 2 L WS5 p p ∑ 2 Π 2 The levels of AH and poly. poly. BPP: Bounded‐Error Probabilistic TAUT = ∃∀ P = ∀∃ P SAT Polynomial Time. Many believe BPP = P. NC1 PH are analogous, NLIN except that we believe NP co‐NP 0 NP ∩ co‐NP ≠ P and NTIME [n2] TC QBF PARITY ∑p ∩Πp NP PP Probabilistic NP FACT 2 2 ≠ P , which NP ACC0 stand in contrast to P PSPACE Polynomial Time MAJ‐SAT CVP RE ∩ co‐RE = REC and 0 AC RE P P ∑2 ∩Π2 = REC GAP NP co‐NP REG NL poly 0 0 ∃ .
    [Show full text]
  • Complexity Classes
    CHAPTER Complexity Classes In an ideal world, each computational problem would be classified at least approximately by its use of computational resources. Unfortunately, our ability to so classify some important prob- lems is limited. We must be content to show that such problems fall into general complexity classes, such as the polynomial-time problems P, problems whose running time on a determin- istic Turing machine is a polynomial in the length of its input, or NP, the polynomial-time problems on nondeterministic Turing machines. Many complexity classes contain “complete problems,” problems that are hardest in the class. If the complexity of one complete problem is known, that of all complete problems is known. Thus, it is very useful to know that a problem is complete for a particular complexity class. For example, the class of NP-complete problems, the hardest problems in NP, contains many hundreds of important combinatorial problems such as the Traveling Salesperson Prob- lem. It is known that each NP-complete problem can be solved in time exponential in the size of the problem, but it is not known whether they can be solved in polynomial time. Whether ? P and NP are equal or not is known as the P = NP question. Decades of research have been devoted to this question without success. As a consequence, knowing that a problem is NP- complete is good evidence that it is an exponential-time problem. On the other hand, if one such problem were shown to be in P, all such problems would be been shown to be in P,a result that would be most important.
    [Show full text]