Topi Uusitalo Single- and Dual-Frequency Laser Diodes Based on Surface Gratings
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ASSESSING the MAINTAINABILITY of C++ SOURCE CODE by MARIUS SUNDBAKKEN a Thesis Submitted in Partial Fulfillment of the Requireme
ASSESSING THE MAINTAINABILITY OF C++ SOURCE CODE By MARIUS SUNDBAKKEN A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Computer Science WASHINGTON STATE UNIVERSITY School of Electrical Engineering and Computer Science DECEMBER 2001 To the Faculty of Washington State University: The members of the Committee appointed to examine the thesis of MARIUS SUNDBAKKEN find it satisfactory and recommend that it be accepted. Chair ii ASSESSING THE MAINTAINABILITY OF C++ SOURCE CODE Abstract by Marius Sundbakken, M.S. Washington State University December 2001 Chair: David Bakken Maintenance refers to the modifications made to software systems after their first release. It is not possible to develop a significant software system that does not need maintenance because change, and hence maintenance, is an inherent characteristic of software systems. It has been estimated that it costs 80% more to maintain software than to develop it. Clearly, maintenance is the major expense in the lifetime of a software product. Predicting the maintenance effort is therefore vital for cost-effective design and development. Automated techniques that can quantify the maintainability of object- oriented designs would be very useful. Models based on metrics for object-oriented source code are necessary to assess software quality and predict engineering effort. This thesis will look at C++, one of the most widely used object-oriented programming languages in academia and industry today. Metrics based models that assess the maintainability of the source code using object-oriented software metrics are developed. iii Table of Contents 1. Introduction .................................................................................................................1 1.1. Maintenance and Maintainability....................................................................... -

Real-Time Multiplayer Software Archi- Tecture
Olli Vilmi Real-time Multiplayer Software Archi- tecture Metropolia University of Applied Sciences Bachelor of Engineering Information and Communications Technology Bachelor’s Thesis 13 March 2020 Abstract Author Olli Vilmi Title Real-time Multiplayer Software Architecture Number of Pages 49 pages + 2 appendices Date 17 February 2020 Degree Bachelor of Engineering Degree Programme Information and Communications Technology Professional Major Software Engineering Instructors Janne Salonen, Head of Department The goal of the project was to study real-time multiplayer programming to identify require- ments, problems and common solutions. Using this information, software architecture was designed and implemented for a 2D platformer game. The programming language Lua was the programming language used for the game client, which runs on the LÖVE2D game framework. Consequently, the server was also written in Lua, but any applicable language could have been chosen. The freedom to be able to use any tools was an important objective of the project. The server model, updating the game state, bandwidth and latency are critical topics which were addressed during the design process. The desired features for networking were imple- mented with simple solutions based on different requirements. Experiences and problems faced during the development are reviewed to show examples of problems and to draw conclusions. In order to prevent packet loss without inducing more latency, features from TCP were implemented on top of a UDP based messaging protocol. Bandwidth -

Application: Unity 3D Web Player
unity3d_1-adv.txt 1 of 2 Application: Unity 3D web player http://unity3d.com/webplayer/ Versions: <= 3.2.0.61061 Platforms: Windows Bug: heap corruption Exploitation: remote Date: 21 Feb 2012 Unity 3d is a game engine used in various games and it’s web player allows to play these games (unity3d extension) also directly from the web browser. # Vulnerabilities # Heap corruption caused by a negative 32bit size value which allows to execute malicious code. The problem is caused by the modification of the 64bit uncompressed size (handled as 32bit by the plugin) of the lzma header which is just composed by the following fields (from lzma86.h): Offset Size Description 0 1 = 0 - no filter, pure LZMA = 1 - x86 filter + LZMA 1 1 lc, lp and pb in encoded form 2 4 dictSize (little endian) 6 8 uncompressed size (little endian) Reading of the 64bit field as 32bit one (CMP EAX,4) and some of the subsequent operations: 070BEDA3 33C0 XOR EAX,EAX 070BEDA5 895D 08 MOV DWORD PTR SS:[EBP+8],EBX 070BEDA8 83F8 04 CMP EAX,4 070BEDAB 73 10 JNB SHORT webplaye.070BEDBD 070BEDAD 0FB65438 05 MOVZX EDX,BYTE PTR DS:[EAX+EDI+5] 070BEDB2 8B4D 08 MOV ECX,DWORD PTR SS:[EBP+8] 070BEDB5 D3E2 SHL EDX,CL 070BEDB7 0196 A4000000 ADD DWORD PTR DS:[ESI+A4],EDX 070BEDBD 8345 08 08 ADD DWORD PTR SS:[EBP+8],8 070BEDC1 40 INC EAX 070BEDC2 837D 08 40 CMP DWORD PTR SS:[EBP+8],40 070BEDC6 ^72 E0 JB SHORT webplaye.070BEDA8 070BEDC8 6A 4A PUSH 4A 070BEDCA 68 280A4B07 PUSH webplaye.074B0A28 ; ASCII "C:/BuildAgen t/work/b0bcff80449a48aa/PlatformDependent/CommonWebPlugin/CompressedFileStream.cp p" 070BEDCF 53 PUSH EBX 070BEDD0 FF35 84635407 PUSH DWORD PTR DS:[7546384] 070BEDD6 6A 04 PUSH 4 070BEDD8 68 00000400 PUSH 40000 070BEDDD E8 BA29E4FF CALL webplaye.06F0179C .. -

Independent Games What They Are and Are They Different
Jaakko Kemppainen Independent games What they are and are they different Master's thesis Digital Culture 20.2.2008 Jyväskylä University Department of Art and Culture Studies Jyväskylä JYVÄSKYLÄN YLIOPISTO Tiedekunta – Faculty Laitos – Department Faculty of Humanities Department of Art and Culture Studies Tekijä – Author Jaakko Kemppainen Työn nimi – Title Independent games What they are and are they different Oppiaine – Subject Työn laji – Level Digital Culture Master's thesis Aika – Month and year Sivumäärä – Number of pages February 2008 98 p. + Appendices 18 p. Tiivistelmä – Abstract This research figures out, how the concept of independent games and independent game production is understood in the field of game industry. Some comparisons are made to music and movie industry, using literature and different internet sources to find out commonly used definitions for independent concept on different areas of entertainment business. Three level definition for independent productions is formed, mainly from the commerce point of view - independent, semi-independent and non-independent games and producers. Second part of this research is a quantitative genre comparison between non-independent games and independent games. For the use of the genre research, a study of game genres is made and basen on that, a game genre systemi is produced. Main finding of the quantitative research is, that independent game genre distribution is different in the case of non-independent games, but there are a lot of similarities within both non-independent and -
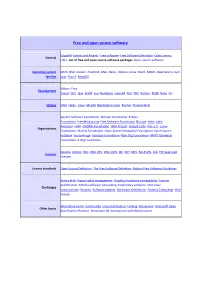
Free and Open Source Software
Free and open source software Copyleft ·Events and Awards ·Free software ·Free Software Definition ·Gratis versus General Libre ·List of free and open source software packages ·Open-source software Operating system AROS ·BSD ·Darwin ·FreeDOS ·GNU ·Haiku ·Inferno ·Linux ·Mach ·MINIX ·OpenSolaris ·Sym families bian ·Plan 9 ·ReactOS Eclipse ·Free Development Pascal ·GCC ·Java ·LLVM ·Lua ·NetBeans ·Open64 ·Perl ·PHP ·Python ·ROSE ·Ruby ·Tcl History GNU ·Haiku ·Linux ·Mozilla (Application Suite ·Firefox ·Thunderbird ) Apache Software Foundation ·Blender Foundation ·Eclipse Foundation ·freedesktop.org ·Free Software Foundation (Europe ·India ·Latin America ) ·FSMI ·GNOME Foundation ·GNU Project ·Google Code ·KDE e.V. ·Linux Organizations Foundation ·Mozilla Foundation ·Open Source Geospatial Foundation ·Open Source Initiative ·SourceForge ·Symbian Foundation ·Xiph.Org Foundation ·XMPP Standards Foundation ·X.Org Foundation Apache ·Artistic ·BSD ·GNU GPL ·GNU LGPL ·ISC ·MIT ·MPL ·Ms-PL/RL ·zlib ·FSF approved Licences licenses License standards Open Source Definition ·The Free Software Definition ·Debian Free Software Guidelines Binary blob ·Digital rights management ·Graphics hardware compatibility ·License proliferation ·Mozilla software rebranding ·Proprietary software ·SCO-Linux Challenges controversies ·Security ·Software patents ·Hardware restrictions ·Trusted Computing ·Viral license Alternative terms ·Community ·Linux distribution ·Forking ·Movement ·Microsoft Open Other topics Specification Promise ·Revolution OS ·Comparison with closed -

Novel Applications of Real-Time Audiovisual Signal Processing Technology for Art and Sports Education and Entertainment
Helsinki University of Technology Publications in Telecommunications Software and Multimedia Teknillisen korkeakoulun tietoliikenneohjelmistojen ja multimedian julkaisuja Espoo 2007 TML-A18 NOVEL APPLICATIONS OF REAL-TIME AUDIOVISUAL SIGNAL PROCESSING TECHNOLOGY FOR ART AND SPORTS EDUCATION AND ENTERTAINMENT Perttu Hämäläinen Dissertation for the degree of Doctor of Science in Technology to be presented with due permission of the Department of Computer Science and Engineering, for public examination and debate in Auditorium T2 at Helsinki University of Technology (Espoo, Finland) on the 30th of March, 2007, at 12 noon. Helsinki University of Technology Department of Computer Science and Engineering Telecommunications Software and Multimedia Laboratory Teknillinen korkeakoulu Tietotekniikan osasto Tietoliikenneohjelmistojen ja multimedian laboratorio Distribution: Helsinki University of Technology Telecommunications Software and Multimedia Laboratory P.O.Box 5400 FIN-02015 TKK URL: http://www.tml.tkk.fi Tel. +358-9-451 2870 Fax. +358-9-451 5014 © 2007 Perttu Hämäläinen ISBN 978-951-22-8704-8 ISBN 978-951-22-8705-5 (PDF) ISSN 1456-7911 ISSN 1455-9722 (PDF) URL: http://lib.tkk.fi/Diss/2007/isbn9789512287055/ Multiprint Oy/Otamedia Espoo 2007 2 ABSTRACT Author Perttu Hämäläinen Title Novel applications of real-time audiovisual signal processing technology for art and sports education and entertainment This thesis explores the possibilities of real-time audiovisual signal processing in the context of human-computer interfaces. Novel embodied -

Gazeta Power
GAZETA POWER The official Liero Community Magazine ISSUE #5 - 2006 THE ISSUE WITH THE IRRELEVANT FRONT PAGE LEARN TO LOVE THE SPIKEBALLS LIERONET IS GONE NOW LIEROX, ENHANCED FABULOUS INTERVIEW with Social Poison Nothing Special | Servers move Walking over games? | Liero.fm Most recent ComSer Column ComSer Polls What is ComSer? Do you sleep enough? ComSer means “Community Ser- No, too little .......................................281 vice” and refers to the Liero Com- Yes, I do .............................................162 munty. The full name is therefor Well, too much ....................................42 “The Liero Community Service”. Total votes: 485 What does it do? Next planet they discover ComSer’s main function is to ap- should be named after Liero pear as a sidebar or box in a web- Yes! ....................................................332 site in which it displays the ComSer Huh? ....................................................81 newsfeed. The newsfeed comes No ........................................................72 from the ComSer Forum, and Total votes: 485 the news are posted by admins. Therefor the webmasters that use Next hyperm33t should be in... ComSer on their sites do not need Warsaw ..............................................100 to update news on their own. Its all Amsterdam ..........................................63 centralized. Plus, it is completely Oslo .....................................................54 skinnable to fit any website. Kansas City .........................................40 Berlin -

Of 81 /Users/Tom/Desktop/Games.Txt Saved
/Users/tom/Desktop/games.txt Page 1 of 81 Saved: 2/6/14, 12:31:18 AM Printed For: Tom Tostanoski 1 1 To Nil Soccer Manager (1992)(Wizard Games Of Scotland Ltd) 2 1000 Miglia (1991)(Simulmondo) 3 100000 Pyramid (1988)(Basada) 4 10th Frame (1986)(Access Software Inc) 5 15x15 Picture Puzzle (1996)(Freeware) 6 1830 Railroads And Robber Barons (1995)(Avalon Interactive) 7 1869 (1992)(Max Design) 8 1942 Pacific Air War Scenario Disk (1995)(Microprose Software) 9 1942 The Pacific Air War (1994)(Microprose Software Inc) 10 1942 The Pacific Air War (1994)(Microprose Software Inc)(Rev1) 11 20000 Leagues Under The Sea (1988)(Coktel Vision) 12 221 B Baker St (1986)(Datasoft Inc) 13 2400 Ad (1987)(Origin Systems Inc) 14 3 Demon (1983)(Pc Research) 15 3 Point Basketball (1994)(MVP Software) 16 3d Ball Blaster (1992)(Dungeon Entertainment) 17 3d Beauty Jessica Sewell (1994)(Playboy)(3d goggles) 18 3d Body Adventure (1994)(Knowledge Adventure Levande Bocker) 19 3d Construction Set 1 (1991)(Domark) 20 3d Construction Set 2 (1992)(Domark) 21 3d Cyber Blaster (1994)(Dungeon Entertainment) 22 3d Cyberpuck (1995)(Dungeon Entertainment) 23 3d Dinosaur Multimedia (1994)(Knowledge Adventure) 24 3d Helicopter Simulator (1987)(Sierra Online) 25 3d Helicopter Simulator 1.10 (1987)(Sierra Online)(Rev) 26 3d Table Sports (1995)(Time Warner Interactive) 27 3d World Boxing (1992)(Simulmondo) 28 4 Queens Computer Casino (1992)(Applications Plus) 29 43D Nightmares (1996)(Visioneer) 30 4d Boxing (1991)(Mindscape Inc)(Rev1) 31 4d Boxing (1991)(Mindscape Inc)(Rev2) 32 4d -

BAKAL´AˇRSK´A PR´ACE David Slabý Ditchers
Univerzita Karlova v Praze Matematicko-fyzik´aln´ıfakulta BAKALA´ RSKˇ A´ PRACE´ David Slab´y Ditchers Katerda aplikovan´ematematiky Vedouc´ıbakal´aˇrsk´epr´ace:RNDr. Bernard Lidick´y Studijn´ıprogram: Informatika, obecn´ainformatika 2010 DˇekujiRNDr. Bernardovi Lidick´emu za veden´ıt´etobakal´aˇrsk´epr´acea za mnoh´euˇziteˇcn´erady. D´alebych r´adpodˇekoval Janu Jeron´ymovi Zv´anovci za tvorbu bal´ıˇck˚upro Debian, sv´emanˇzelceAlˇzbˇetˇeza tvorbu hezk´ehern´ı grafiky a tak´evˇsempˇr´atel˚um,kteˇr´ı byli ochotni projekt testovat a mˇeli k nˇemu cenn´epˇripom´ınky. Prohlaˇsuji,ˇzejsem svou bakal´aˇrskou pr´acinapsal samostatnˇea v´yhradnˇe s pouˇzit´ımcitovan´ych pramen˚u.Souhlas´ımse zap˚ujˇcov´an´ımpr´acea jej´ım zveˇrejˇnov´an´ım. V Praze dne 23. kvˇetna2010 David Slab´y 2 Contents 1 Introduction 6 2 Game 8 2.1 Graphic User Interface . 8 2.1.1 Splash screen . 8 2.1.2 GUI windows . 9 2.1.3 Main window . 9 2.1.4 Graphics settings window . 9 2.1.5 Players management window . 10 2.1.6 Game creation window . 11 2.1.7 Game lobby window . 11 2.1.8 Network connection window . 12 2.1.9 Server lobby window . 13 2.1.10 Credits window . 14 2.2 Gameplay . 14 2.2.1 Maps . 14 2.2.2 Game screen . 15 2.2.3 Map view . 15 2.2.4 Health and energy . 16 2.2.5 Robot movement . 17 2.2.6 Weapons . 17 2.2.7 Score . 20 2.2.8 Chatting and logging . 20 2.2.9 Spectator mode . -

Stochastic Processes an Introduction Third Edition CHAPMAN & HALL/CRC Texts in Statistical Science Series Series Editors Joseph K
Stochastic Processes An Introduction Third Edition CHAPMAN & HALL/CRC Texts in Statistical Science Series Series Editors Joseph K. Blitzstein, Harvard University, USA Julian J. Faraway, University of Bath, UK Martin Tanner, Northwestern University, USA Jim Zidek, University of British Columbia, Canada Statistical Theory: A Concise Introduction Problem Solving: A Statistician’s Guide, F. Abramovich and Y. Ritov Second Edition Practical Multivariate Analysis, Fifth Edition C. Chatfield A. Afifi, S. May, and V.A. Clark Statistics for Technology: A Course in Applied Practical Statistics for Medical Research Statistics, Third Edition D.G. Altman C. Chatfield Interpreting Data: A First Course Analysis of Variance, Design, and Regression : in Statistics Linear Modeling for Unbalanced Data, A.J.B. Anderson Second Edition R. Christensen Introduction to Probability with R K. Baclawski Bayesian Ideas and Data Analysis: An Introduction for Scientists and Statisticians Linear Algebra and Matrix Analysis for Statistics R. Christensen, W. Johnson, A. Branscum, S. Banerjee and A. Roy and T.E. Hanson Modern Data Science with R Modelling Binary Data, Second Edition B. S. Baumer, D. T. Kaplan, and N. J. Horton D. Collett Mathematical Statistics: Basic Ideas and Modelling Survival Data in Medical Research, Selected Topics, Volume I, Third Edition Second Edition D. Collett P. J. Bickel and K. A. Doksum Introduction to Statistical Methods for Mathematical Statistics: Basic Ideas and Clinical Trials Selected Topics, Volume II T.D. Cook and D.L. DeMets P. J. Bickel and K. A. Doksum Applied Statistics: Principles and Examples Analysis of Categorical Data with R D.R. Cox and E.J. Snell C. R. -

Multiplayer on One Screen Framework
Multiplayer On One Screen a framework for multiplayer games on one screen SVERRE MORKA ALEKSANDER BAUMANN SPRO MORTEN VERSVIK Master of Science in Computer Science Prestudy Submission date: Fall 2006 Supervisor: ALF INGE WANG, IDI Norwegian University of Science and Technology Department of Computer and Information Science Abstract The goal of this depth study is to look into infrastructure to support a new concept; multiplayer on one screen (MOOS) games. This concept is especially well suited for cinemas which just recently were analogue but are rapidly becoming digital. The concept can also be used in other contexts such as arcade games. The report starts by looking into previous/related work that is comparable to this new concept. We continue with evaluating technology that has to be used to make the concept possible. Further, we look into how we can make a framework which abstracts the required network support and gives possibilities for more features without making the development of games on the platform more difficult. Another important part is what kind of games can be used in the concept. As there is currently not done any research into this work before, we describe what parts from different game genres fit in the concept, and come up with a game concepts that fits good. To validate the principles of the framework, we made an implementation of the framework and tested it with all the required technology. Some pictures, a video from the session, a standalone binary of the game and source code is included. This thesis is tied-up and should not be given or shown to any other person than the external examiner, Alf Inge Wang, Morten Versvik, Sverre Morka or Aleksander Spro without any permission granted by Alf Inge Wang, Morten Versvik, Sverre Morka and Aleksander Spro. -

Elegant Letter
Brown County, Minnesota Board of Commissioners P.O. Box 248 Center & State Streets New Ulm, MN 56073 Telephone (507) 233-6600 District 1: David Borchert 405 South Broadway St. BOARD OF BROWN COUNTY COMMISSIONERS New Ulm, MN 56073 REGULAR MEETING – August 28, 2018 AGENDA: District 2: Anton Berg 20218 195th Ave 9:00 AM 1. Approve County Board Official Proceedings and Synopsis of 08-21-18 New Ulm, MN 56073 2. Set Closed Session for Labor Negotiations Strategy Planning 9:01 AM Human Services Chemical Dependency Counselor Leah Luke Probation Department Chemical Dependency Counselor LuAnn Macho District 3: Scott Windschitl 3. Chemical Dependency Treatment Fund Annual Report/DAANES County 10 Doris Drive New Ulm, MN 56073 Chemical Dependency Statistics 2017 9:20 AM Underage Substance Abuse Coalition Coordinator Abigail Schwab 4. Underage Substance Abuse Coalition Presentation District 4: 9:35 AM Children & Families Social Services Supervisor Denise Kamm Dean Simonsen 28711 310th Ave. Childcare Licensor Alesia Slater Sleepy Eye, MN 56085 5. Childcare Licensing Fees Changes 9:45 AM Human Services Director Tom Henderson District 5: 6. Human Services Claim Payments Dennis Potter 40520 US Highway 14 7. Correspondence and Consent Agenda Items Springfield, MN 56087 10:25 AM BREAK 10:30 AM HR Director Ruth Schaefer 8. Human Services Office Support Specialist Resignation/Retirement 10:32 AM Highway Engineer Wayne Stevens 9. Resolution − Proposal for a Historian for Bridge 2110 on CSAH 8 10:35 AM Auditor/Treasurer Jean Prochniak Assistant Highway Engineer Andrew Lang 10. Drainage Ditch Repair Request 10:40 AM Auditor/Treasurer Jean Prochniak 11. SpyGlass Snapshot Audit Agreement 12.