DOCSLIB.ORG

Optimal Design of Compliant Trailing Edge for Shape Changing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optimal Design of Compliant Trailing Edge for Shape Changing Chinese Journal of Aeronautics Chinese Journal of Aeronautics 21(2008) 187-192 www.elsevier.com/locate/cja Optimal Design of Compliant Trailing Edge for Shape Changing Liu Shili, Ge Wenjie*, Li Shujun School of Mechatronics, Northwestern Polytechnical University, Xi’an 710072, China Received 19 July 2007; accepted 2 January 2008 Abstract Adaptive wings have long used smooth morphing technique of compliant leading and trailing edge to improve their aerodynamic characteristics. This paper introduces a systematic approach to design compliant structures to carry out required shape changes under distributed pressure loads. In order to minimize the deviation of the deformed shape from the target shape, this method uses MATLAB and ANSYS to optimize the distributed compliant mechanisms by way of the ground approach and genetic algorithm (GA) to remove the elements possessive of very low stresses. In the optimization process, many factors should be considered such as airloads, input dis- placements, and geometric nonlinearities. Direct search method is used to locally optimize the dimension and input displacement after the GA optimization. The resultant structure could make its shape change from 0 to 9.3 degrees. The experimental data of the model confirms the feasibility of this approach. Keywords: adaptive wing; compliant mechanism; genetic algorithm; topology optimization; distributed pressure load; geometric nonlin- earity 1 Introduction* changing. Nevertheless, compared to the compliant mechanism, the smart-material-made actuators have As conventional airfoil contours are usually many disadvantages, such as deficient in energy, designed with specific lift coefficients and Mach slow in response, strong in hysteresis, limited by numbers, they could not change in accordance with temperature, and difficult to control too many ac- the environment changing. Siclari and Austin[1] in- tuators. Musolff[2] from Industry University of Ber- dicated that the variable camber trailing edge would lin used Ni-Ti shape-memory-alloy wire to make an produce the drag about sixty percent less than the adaptive variable camber wing, which could quickly conventional fixed camber airfoil. change its shape, but could not perform highly fre- There are three methods used to design vari- quent alteration because of its resilience dependent able camber wings. Of them, one is conventional on the heat exchange with the outside environment. hinged mechanism, which, however, will create Compliant mechanism is a kind of one-piece discontinuities over the wing’s surface leading to flexible structure, which can transfer motion and earlier airflow separation and drag increase. The power through its own elastic deformation. It is not others are smart material and the compliant mecha- only flexible enough to deform, but also has enough nism, of which both could realize smooth shape stiffness to withstand external loads. Thanks to its *Corresponding author. Tel.: +86-29-88493929. joint-free nature, it does not have the troublesome E-mail address:[email protected] Foundation item: National Natural Science Foundation of China problems confronted by conventional mechanism, (50675175) · 188 · Liu Shili et al. / Chinese Journal of Aeronautics 21(2008) 187-192 such as friction, lubrication, noise and recoiling, This paper presents a method to design the thereby achieving smooth shape changing. shape changeable structure by MATLAB and AN- In 1994, Kota[3], a professor from University of SYS associated with distributed compliant mecha- Michigan, firstly pointed out that compliant mecha- nism on the base of the ground structure approach nism could be used to control static shape changing and genetic algorithm (GA) taking into account the under the sponsorship of the Air Force Office of external distributed loads and geometric nonlinear- Scientific Research in USA. Saggere and Kota[4] ity. suggested a new method to design compliant adap- tive structures, which made the least square errors 2 Optimization Process between the shape-changed curve and the target 2.1 Defining the trailing edge model and ob- curve as the objective function for optimization. jective function Based on their work, Lu[5] put forward a load path representation method. However, her work was lim- As shown in Fig.1, both curves represent two ited to only linear analysis under consideration of ideal shapes of the trailing edge in the different fly- nodal loads. Good[6] from Virginia Polytechnic In- ing states. One side (A point) of the structure is stitute of State University used the compliant supposed to be fixed, and the other side (B point) to mechanism and the Moving Asymptotes method to be sliding horizontally. design the fuselage tail within the allowable range of its tip maximal deflection. Kota and Hetrick[7] in 2004 designed a compliant trailing edge on the base of the F16’s data, which can change from 0° to 15° and obtained a patent. Campanile[8] from German Aerospace Center presented a modal procedure to design synthetic flexible mechanisms for airfoil shape control, and pointed out that the future re- search should take into account the airload and the Fig.1 Initial shape and target shape. geometric nonlinearity. Buhl[9] from Risø National Firstly, the design domain should be defined by Laboratory of the Wind Energy Department in the initial curve shape, the input location and the Denmark used the SIMP method and geometrically boundary conditions. Then, it is divided with a nonlinear finite element method to design compliant beam element network simulating the bird’s feather trailing edge flaps. FlxSys Inc in 2006 produced an as shown in Fig.2. This is termed the partial ground adaptive compliant wing, which stood the test on structure method. the White Knight airplane. The results indicated that the compliant trailing edge could change ±10°[10]. In China, the research of adaptive wing has been con- centrated on smart material and conventional mechanism. Few people, it seems, have worked on designing adaptive wings with the compliant mechanism. Yang is an exception. He analyzed the Fig.2 Discretization of the design domain. active aero-elastic wings based on the aero-servo- elasticity technology[11]. Chen and Huang separately The simplest and most effective way to manu- investigated the morphing of the compliant leading facture the planar compliant mechanism is to use edge from the viewpoints of discreteness and conti- wire-cutting technology. In the optimization pro- nuity[12-13]. gram, all the elements are of rectangular beams with Liu Shili et al. / Chinese Journal of Aeronautics 21(2008) 187-192 · 189 · the same width equal to the thickness of the material, method, it does not require the gradient-based in- every beam’s height being a design variable. formation of the objective function. In order to make the structure’s deformation Every element could be expressed as a topo- come close to the target shape curve, the least logy variable and a dimension variable[5]. There- square error (LSE) between the deformed curve and foreˈeach individual could be coded as follows the target curve is defined as the objective function. U=>TT12 Tinn T 1 T LSE is the sum of squares of position differences of hh12"" hinn h 1 h h b@ (7) various points along the curves[5]. Its expression is p where n is the number of elements except the 22 minfx ( ) ¦ ( xTar,ii x Def, ) ( y Tar, ii y Def, ) (1) boundary ones. With the same heights, the boundary i 1 elements throughout the optimizing process are where i (=1, 2, ···, p) is the number of the points represented by only one variable, hb. along the curves, p is the total number of points. The fitness is the criterion of the GA optimiza- (xTar,i, yTar,i) and (xDef,i, yDef,i) are the coordinates of tion. It could be transformed from the objective ith node on the target and deformed boundary curve function into[12] respectively. Fit(f (xfx )) exp(E ( )) (8) The constraints are hmin < hi < hmax (2) where E is a coefficient deciding the compulsive hmin < hb < hmax (3) selection of the better individual. The smaller the ddmax d [] (4) value, the more different would be between the two VVmaxd s (5) individuals’ fitness thus increasing the compulsive- ness of choosing the individual of higher fitness. Tj {0,1} (6) The selection of control parameters plays an where j (=1, 2, ···, m) is the number of elements, m important role in the convergence of the GA. Gen- is the total number of elements, hi the dimension erally speaking, the cross probability ranges 0.40- variable, hmin and hmax are the lower and upper 0.99; the mutation probability is 0.000 01-0.01, and bounds of the element beam height for all elements the number of individuals 10-200. with the value dependent on manufacturing, hb the The variable would be updated through the height of the boundary elements, dmax the maximum crossover and mutation, so the possible design could nodal deformation of the nodes on the curve bound- generate in the GA process. ary when the input point is inactive, and should be 2.3 Finite element analysis (FEA) smaller than [d] to ensure structure stiffness, [d] the allowable maximum displacement when the input Because of the limited design variables and the point is inactive, Vmax the maximum stress of all the target function, the optimization module of FEA elements which must be smaller than Vs to prevent software could not be used to design the compliant yielding, Tj the topology variable equal to 1, or else morphing mechanism. Therefore, this paper pro- 0 when the element is eliminated. grammed the GA in MATLAB and the FEA in ANSYS. In the FEA, taking only account of geo- 2.2 GA optimization metric nonlinearities and the material being of linear GA is an optimization method which simulates elasticity, ANSYS could solve the node displace- the heuristic selection rule in nature, where the fit- ments and the element stresses.
Load more

Recommended publications
  • University of Oklahoma Graduate College Design and Performance Evaluation of a Retractable Wingtip Vortex Reduction Device a Th
    UNIVERSITY OF OKLAHOMA GRADUATE COLLEGE DESIGN AND PERFORMANCE EVALUATION OF A RETRACTABLE WINGTIP VORTEX REDUCTION DEVICE A THESIS SUBMITTED TO THE GRADUATE FACULTY In partial fulfillment of the requirements for the Degree of Master of Science Mechanical Engineering By Tausif Jamal Norman, OK 2019 DESIGN AND PERFORMANCE EVALUATION OF A RETRACTABLE WINGTIP VORTEX REDUCTION DEVICE A THESIS APPROVED FOR THE SCHOOL OF AEROSPACE AND MECHANICAL ENGINEERING BY THE COMMITTEE CONSISTING OF Dr. D. Keith Walters, Chair Dr. Hamidreza Shabgard Dr. Prakash Vedula ©Copyright by Tausif Jamal 2019 All Rights Reserved. ABSTRACT As an airfoil achieves lift, the pressure differential at the wingtips trigger the roll up of fluid which results in swirling wakes. This wake is characterized by the presence of strong rotating cylindrical vortices that can persist for miles. Since large aircrafts can generate strong vortices, airports require a minimum separation between two aircrafts to ensure safe take-off and landing. Recently, there have been considerable efforts to address the effects of wingtip vortices such as the categorization of expected wake turbulence for commercial aircrafts to optimize the wait times during take-off and landing. However, apart from the implementation of winglets, there has been little effort to address the issue of wingtip vortices via minimal changes to airfoil design. The primary objective of this study is to evaluate the performance of a newly proposed retractable wingtip vortex reduction device for commercial aircrafts. The proposed design consists of longitudinal slits placed in the streamwise direction near the wingtip to reduce the pressure differential between the pressure and the suction sides.
    [Show full text]
  • Electrically Heated Composite Leading Edges for Aircraft Anti-Icing Applications”
    UNIVERSITY OF NAPLES “FEDERICO II” PhD course in Aerospace, Naval and Quality Engineering PhD Thesis in Aerospace Engineering “ELECTRICALLY HEATED COMPOSITE LEADING EDGES FOR AIRCRAFT ANTI-ICING APPLICATIONS” by Francesco De Rosa 2010 To my girlfriend Tiziana for her patience and understanding precious and rare human virtues University of Naples Federico II Department of Aerospace Engineering DIAS PhD Thesis in Aerospace Engineering Author: F. De Rosa Tutor: Prof. G.P. Russo PhD course in Aerospace, Naval and Quality Engineering XXIII PhD course in Aerospace Engineering, 2008-2010 PhD course coordinator: Prof. A. Moccia ___________________________________________________________________________ Francesco De Rosa - Electrically Heated Composite Leading Edges for Aircraft Anti-Icing Applications 2 Abstract An investigation was conducted in the Aerospace Engineering Department (DIAS) at Federico II University of Naples aiming to evaluate the feasibility and the performance of an electrically heated composite leading edge for anti-icing and de-icing applications. A 283 [mm] chord NACA0012 airfoil prototype was designed, manufactured and equipped with an High Temperature composite leading edge with embedded Ni-Cr heating element. The heating element was fed by a DC power supply unit and the average power densities supplied to the leading edge were ranging 1.0 to 30.0 [kW m-2]. The present investigation focused on thermal tests experimentally performed under fixed icing conditions with zero AOA, Mach=0.2, total temperature of -20 [°C], liquid water content LWC=0.6 [g m-3] and average mean volume droplet diameter MVD=35 [µm]. These fixed conditions represented the top icing performance of the Icing Flow Facility (IFF) available at DIAS and therefore it has represented the “sizing design case” for the tested prototype.
    [Show full text]
  • Self-Actuating Flaps on Bird and Aircraft Wings 437
    Self-actuating flaps on bird and aircraft wings D.W. Bechert, W. Hage & R. Meyer Department of Turbulence Research, German Aerospace Center (DLR), Berlin, Germany. Abstract Separation control is also an important issue in biology. During the landing approach of birds and in flight through very turbulent air, one observes that the covering feathers on the upper side of bird wings tend to pop up. The raised feathers impede the spreading of the flow separation from the trailing edge to the leading edge of the wing. This mechanism of separation control by bird feathers is described in detail. Self-activated movable flaps (= artificial bird feathers) represent a high-lift system enhancing the maximum lift of airfoils up to 20%. This is achieved without perceivable deleterious effects under cruise conditions. Several data of wind tunnel experiments as well as flight experiments with an aircraft with laminar wing and movable flaps are shown. 1 Movable flaps on wings: artificial bird feathers The issue of artificial feathers on wings, has an almost anecdotal origin. Wolfgang Liebe, the inventor of the boundary layer fence once observed mountain crows in the Alps in the 1930s. He noticed that the covering feathers on the upper side of the wings tend to pop up when the birds were on landing approach or in other situations with high angle of attack, like flight through gusts. Once the attention of the observer is drawn to it, it is comparatively easy to observe this behaviour in almost any bird (see, for example, the feathers on the left-hand wing of a Skua in Fig.
    [Show full text]
  • Flexfloil Shape Adaptive Control Surfaces—Flight Test and Numerical Results
    FLEXFLOIL SHAPE ADAPTIVE CONTROL SURFACES—FLIGHT TEST AND NUMERICAL RESULTS Sridhar Kota∗ , Joaquim R. R. A. Martins∗∗ ∗FlexSys Inc. , ∗∗University of Michigan Keywords: FlexFoil, adaptive compliant trailing edge, flight testing, aerostructural optimization Abstract shape-changing control surface technologies has been realized by the ACTE program in which the The U.S Air Force and NASA recently concluded high-lift flaps of the Gulfstream III test aircraft a series of flight tests, including high speed were replaced by a 19-foot spanwise FlexFoilTM (M = 0:85) and acoustic tests of a Gulfstream III variable-geometry control surfaces on each wing, business jet retrofitted with shape adaptive trail- including a 2 ft wide compliant fairings at each ing edge control surfaces under the Adaptive end, developed by FlexSys Inc. The flight tests Compliant Trailing Edge (ACTE) program. The successfully demonstrated the flight-worthiness long-sought goal of practical, seamless, shape- of the variable geometry control surfaces. changing control surface technologies has been Modern aircraft wings and engines have realized by the ACTE program in which the high- reached near-peak levels of efficiency, making lift flaps of the Gulfstream III test aircraft were further improvements exceedingly difficult. The replaced with 23 ft spanwise FlexFoilTM variable next frontier in improving aircraft efficiency is to geometry control surfaces on each wing. The change the shape of the aircraft wing in-flight to flight tests successfully demonstrated the flight- maximize performance under all operating con- worthiness of the variable geometry control sur- ditions. Modern aircraft wing design is a com- faces. We provide an overview of structural and promise between several constraints and flight systems design requirements, test flight envelope conditions with best performance occurring very (including critical design and test points), re- rarely or purely by chance.
    [Show full text]
  • Feb. 14, 1939. E
    Feb. 14, 1939. E. F. ZA PARKA 2,147,360 AIRPLANE CONTROL APPARATUS Original Filed Feb. 16, 1933 7 Sheets-Sheet Feb. 14, 1939. E. F. ZA PARKA 2,147,360 AIRPLANE CONTROL APPARATUS Original Filed Feb. 16, 1933 7 Sheets-Sheet 2 &tkowys Feb. 14, 1939. E. F. zAPARKA 2,147,360 ARP ANE CONTROL APPARATUS Original Filed Feb. 16, 1933 7 Sheets-Sheet 3 Wr a NSeta ?????? ?????????????? "??" ?????? ??????? 8tkowcA" Feb. 14, 1939. E. F. ZA PARKA 2,147,360 AIRPLANE CONTROL APPARATUS Original Filled Feb. 16, 1933 7 Sheets-Sheet 4 Feb. 14, 1939. E. F. ZA PARKA 2,147,360 AIRPLANE CONTROL APPARATUS Original Filed. Feb. l6, l933 7 Sheets-Sheet 5 3. 8. 2. 3 Feb. 14, 1939. E. F. ZA PARKA 2,147,360 AIRPANE CONTROL APPARATUS Original Filled Feb. 16, 1933 7 Sheets-Sheet 6 M76, az 42a2/22/22a/7 ?tows Feb. 14, 1939. E. F. ZAPARKA 2,147,360 AIRPANE CONTROL APPARATUS Original Filled Feb. l6, l933 7 Sheets-Sheet 7 Jway/7 -ZWAZZ/JAZZA/ Juventor. Zff60 / Ze/7 384 ?r re? Patented Feb. 14, 1939 2,147,360 UNITED STATES PATENT OFFICE AIRPLANE CONTRO APPARATUS Edward F. Zaparka, Baltimore, Md., assignor to Zap Development Corporation, Baltimore, Md., a corporation of Delaware Application February 16, 1933, serial No. 657,133 Renewed February 1, 1937 4. Claims. (CI. 244—42) My invention relates to aircraft construction, parting from the spirit and scope of the appended and in particular relates to the control of aircraft claims, equipped with Wing flaps which Operate in the In order to make my invention more clearly Zone of optimum efficency.
    [Show full text]
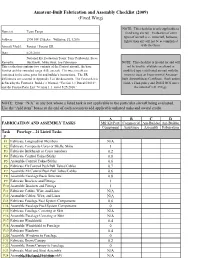
  • Amateur-Built Fabrication and Assembly Checklist (2009) (Fixed Wing)
    Amateur-Built Fabrication and Assembly Checklist (2009) (Fixed Wing) NOTE: This checklist is only applicable to Name(s) Team Tango fixed wing aircraft. Evaluation of other types of aircraft (i.e., rotorcraft, balloons, Address: 1990 SW 19th Ave. Williston, FL 32696 lighter than air) will not be accomplished Aircraft Model: Foxtrot / Foxtrot ER with this form. Date: 6/23/2010 National Kit Evaluation Team: Tony Peplowski, Steve Remarks: Buczynski, Mike Sloat, Joe Palmisano NOTE: This checklist is invalid for and will This evaluation contains two variants of the Foxtrot aircraft, the base not be used to evaluate an altered or Foxtrot and the extended range (ER) aircraft. The two aircraft are modified type certificated aircraft with the contained in the same parts list and builder's instructions. The ER intent to issue an Experimental Amateur- differences are covered in Appendix 5 of the document. The Foxtrot kit is built Airworthiness Certificate. Such action defined by the Foxtrot 4 Builder’s Manual, “Version 1.1 Dated 5/2010”, violates FAA policy and DOES NOT meet and the Foxtrot Parts List “Version 1.1. dated 5/25/2010.” the intent of § 21.191(g). NOTE: Enter “N/A” in any box where a listed task is not applicable to the particular aircraft being evaluated. Use the “Add item” boxes at the end of each section to add applicable unlisted tasks and award credit. ABCD FABRICATION AND ASSEMBLY TASKS Mfr Kit/Part/ Commercial Am-Builder Am-Builder Component Assistance Assembly Fabrication Task Fuselage – 24 Listed Tasks # F1 Fabricate Longitudinal
    [Show full text]
  • On Aircraft Trailing Edge Noise
    NEAT Consulting On Aircraft Trailing Edge Noise Yueping Guo NEAT Consulting, Seal Beach, CA 90740 USA and Russell H. Thomas NASA Langley Research Center, Hampton, VA 23681 USA Future Aircraft Design and Noise Impact 22nd Workshop of the Aeroacoustics Specialists Committee of the CEAS 6 – 7 September 2018 Netherlands Aerospace Centre – Amsterdam Acknowledgments NEAT Consulting • Aircraft Noise Reduction (ANR) Subproject of the Advanced Air Transport Technology (AATT) Project for funding this research 2 Outline NEAT Consulting • Introduction • Trailing edge noise data • Prediction methods • Estimate of HWB trailing edge noise • Summary 3 Introduction NEAT Consulting • Significant noise reduction opportunities for future aircraft have been investigated for the major airframe noise sources • Is trailing edge noise the noise floor? – Need reliable data and/or prediction tool to assess its relative importance • Objectives of this presentation – Review currently available data and prediction methods – Illustrate importance of trailing edge noise for future aircraft by preliminary estimate for the Hybrid-Wing- Body (HWB) aircraft 4 Airframe Noise Reduction NEAT Consulting • Thomas R. H., Burley C.L. and Guo Y. P., “Potential for Landing Gear Noise Reduction on Advanced Aircraft Configurations,” AIAA 2016-3039 • Thomas R. H., Guo Y. P., Berton J. J. and Fernandez H., “Aircraft Noise Reduction Technology Roadmap Toward Achieving the NASA 2035 Noise Goal,” AIAA 2017-3193 • Guo Y. P., Thomas R. H., Clark I.A. and June J.C., “Far Term Noise Reduction
    [Show full text]
  • Design Study of a Supersonic Business Jet with Variable Sweep Wings
    27TH INTERNATIONAL CONGRESS OF THE AERONAUTICAL SCIENCES DESIGN STUDY OF A SUPERSONIC BUSINESS JET WITH VARIABLE SWEEP WINGS E.Jesse, J.Dijkstra ADSE b.v. Keywords: swing wing, supersonic, business jet, variable sweepback Abstract A design study for a supersonic business jet with variable sweep wings is presented. A comparison with a fixed wing design with the same technology level shows the fundamental differences. It is concluded that a variable sweep design will show worthwhile advantages over fixed wing solutions. 1 General Introduction Fig. 1 Artist impression variable sweep design AD1104 In the EU 6th framework project HISAC (High Speed AirCraft) technologies have been studied to enable the design and development of an 2 The HISAC project environmentally acceptable Small Supersonic The HISAC project is a 6th framework project Business Jet (SSBJ). In this context a for the European Union to investigate the conceptual design with a variable sweep wing technical feasibility of an environmentally has been developed by ADSE, with support acceptable small size supersonic transport from Sukhoi, Dassault Aviation, TsAGI, NLR aircraft. With a budget of 27.5 M€ and 37 and DLR. The objective of this was to assess the partners in 13 countries this 4 year effort value of such a configuration for a possible combined much of the European industry and future SSBJ programme, and to identify critical knowledge centres. design and certification areas should such a configuration prove to be advantageous. To provide a framework for the different studies and investigations foreseen in the HISAC This paper presents the resulting design project a number of aircraft concept designs including the relevant considerations which were defined, which would all meet at least the determined the selected configuration.
    [Show full text]
  • Static and Dynamic Performance of a Morphing Trailing Edge Concept with High-Damping Elastomeric Skin
    aerospace Article Static and Dynamic Performance of a Morphing Trailing Edge Concept with High-Damping Elastomeric Skin Maurizio Arena 1,*, Christof Nagel 2, Rosario Pecora 1,* , Oliver Schorsch 2 , Antonio Concilio 3 and Ignazio Dimino 3 1 Department of Industrial Engineering—Aerospace Division, University of Naples “Federico II”, Via Claudio, 21, 80125 Napoli (NA), Italy 2 Fraunhofer Institute for Manufacturing Technology and Advanced Materials, Wiener Straße 12, D-28359 Bremen, Germany; [email protected] (C.N.); [email protected] (O.S.) 3 Smart Structures Division Via Maiorise, The Italian Aerospace Research Centre, CIRA, 81043 Capua (CE), Italy; [email protected] (A.C.); [email protected] (I.D.) * Correspondence: [email protected] (M.A.); [email protected] (R.P.); Tel.: +39-081-768-3573 (M.A. & R.P.) Received: 18 November 2018; Accepted: 14 February 2019; Published: 19 February 2019 Abstract: Nature has many striking examples of adaptive structures: the emulation of birds’ flight is the true challenge of a morphing wing. The integration of increasingly innovative technologies, such as reliable kinematic mechanisms, embedded servo-actuation and smart materials systems, enables us to realize new structural systems fully compatible with the more and more stringent airworthiness requirements. In this paper, the authors describe the characterization of an adaptive structure, representative of a wing trailing edge, consisting of a finger-like rib mechanism with a highly deformable skin, which comprises both soft and stiff parts. The morphing skin is able to follow the trailing edge movement under repeated cycles, while being stiff enough to preserve its shape under aerodynamic loads and adequately pliable to minimize the actuation power required for morphing.
    [Show full text]
  • Feasibility Study of a Multi-Purpose Aircraft Concept with a Leading-Edge Cross-Flow Fan
    Dissertations and Theses 5-2018 Feasibility Study of a Multi-Purpose Aircraft Concept with a Leading-Edge Cross-Flow Fan Stanislav Karpuk Follow this and additional works at: https://commons.erau.edu/edt Part of the Aerospace Engineering Commons Scholarly Commons Citation Karpuk, Stanislav, "Feasibility Study of a Multi-Purpose Aircraft Concept with a Leading-Edge Cross-Flow Fan" (2018). Dissertations and Theses. 399. https://commons.erau.edu/edt/399 This Thesis - Open Access is brought to you for free and open access by Scholarly Commons. It has been accepted for inclusion in Dissertations and Theses by an authorized administrator of Scholarly Commons. For more information, please contact [email protected]. FEASIBILITY STUDY OF A MULTI-PURPOSE AIRCRAFT CONCEPT WITH A LEADING-EDGE CROSS-FLOW FAN A Thesis Submitted to the Faculty of Embry-Riddle Aeronautical University by Stanislav Karpuk In Partial Fulfillment of the Requirements for the Degree of Master of Science in Aerospace Engineering May 2018 Embry-Riddle Aeronautical University Daytona Beach, Florida i ACKNOWLEDGMENTS I would like to thank Dr Gudmundsson and Dr Golubev for their knowledge, guidance and advising they provided during these two years of the program. I also would like to thank my committee member Dr Engblom for his advice and recommendations. I also want to thank Petr and Marina Kazarin for their support, help and the opportunity to enjoy the Russian community for those two years. This project would not be possible without strong computational power available in ERAU, so I would like to thank all staff and faculty who contributed to development and support of the VEGA cluster.
    [Show full text]
  • Topology Optimization of Large-Scale 3D Morphing Wing Structures
    actuators Article Topology Optimization of Large-Scale 3D Morphing Wing Structures Peter Dørffler Ladegaard Jensen 1,* , Fengwen Wang 1 , Ignazio Dimino 2 and Ole Sigmund 1 1 Department of Mechanical Engineering, Technical University of Denmark, 2800 Kongens Lyngby, Denmark; [email protected] (F.W.); [email protected] (O.S.) 2 Adaptive Structures Technologies, The Italian Aerospace Research Centre, CIRA, Via Maiorise, 81043 Capua, Italy; [email protected] * Correspondence: [email protected] Abstract: This work proposes a systematic topology optimization approach for simultaneously de- signing the morphing functionality and actuation in three-dimensional wing structures. The actuation was modeled by a linear-strain-based expansion in the actuation material. A three-phase material model was employed to represent structural and actuating materials and voids. To ensure both structural stiffness with respect to aerodynamic loading and morphing capabilities, the optimization problem was formulated to minimize structural compliance, while the morphing functionality was enforced by constraining a morphing error between the actual and target wing shape. Moreover, a feature-mapping approach was utilized to constrain and simplify the actuator geometries. A trailing edge wing section was designed to validate the proposed optimization approach. Numerical results demonstrated that three-dimensional optimized wing sections utilize a more advanced structural layout to enhance structural performance while keeping the morphing functionality better than two-dimensional wing ribs. The work presents the first step towards the systematic design of three-dimensional morphing wing sections. Citation: Jensen, P.D.L.; Wang, F.; Dimino, I.; Sigmund, O. Topology Keywords: topology optimization; morphing wing; aerospace design optimization; smart and Optimization of Large-Scale 3D adaptive structures; feature mapping Morphing Wing Structures.
    [Show full text]
  • Aerodynamic Efficiency of High Maneuverable Aircraft Applying Adaptive Wing Trailing Edge Section
    24TH INTERNATIONAL CONGRESS OF THE AERONAUTICAL SCIENCES AERODYNAMIC EFFICIENCY OF HIGH MANEUVERABLE AIRCRAFT APPLYING ADAPTIVE WING TRAILING EDGE SECTION Christian Breitsamter Institute for Fluid Mechanics, Aerodynamics Division, Technische Universität München Boltzmannstrasse 15, 85748 Garching, Germany Keywords: Adaptive wing, high agility aircraft, high angle of attack, force measurements Abstract environmental impacts enforce continuous im- The aerodynamic characteristics of a high- provement of the performance of both civil and agility aircraft of canard-delta wing type are military aircraft. A key issue enhancing the air- analyzed in detail comparing the performance craft efficiency is the use of advanced and adap- obtained by smooth, variable camber wing trail- tive wing technologies (Fig. 1) [1-4]. ing-edge sections versus conventional trailing- The aerodynamic characteristics of adap- edge flaps. Wind tunnel tests are conducted on a tive and form-variable wing elements and multi- detailed model fitted with discrete elements rep- functional control surfaces have been inten- resenting the adaptive wing trailing-edge sec- sively studied in several German and European tions. Force and flow field measurements are research programs [5-8]. Results show increased carried out to study the aerodynamic properties. glide number, reduced drag and improved high Lift, drag and pitching moment coefficients are lift performance. A main focus is on structural evaluated to assess aerodynamic efficiency and concepts for adaptive flap systems as well as for maneuver capabilities. Comparing the data for local surface deformations and the integration of adaptive and conventional flap configurations, related sensors, actuators and controllers in the it is shown that smooth, variable camber results aircraft [9].
    [Show full text]