Drought's Legacy: Multi-Year Hydraulic Deterioration Underlies Widespread
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Kingdom Class Family Scientific Name Common Name I Q a Records
Kingdom Class Family Scientific Name Common Name I Q A Records plants monocots Poaceae Paspalidium rarum C 2/2 plants monocots Poaceae Aristida latifolia feathertop wiregrass C 3/3 plants monocots Poaceae Aristida lazaridis C 1/1 plants monocots Poaceae Astrebla pectinata barley mitchell grass C 1/1 plants monocots Poaceae Cenchrus setigerus Y 1/1 plants monocots Poaceae Echinochloa colona awnless barnyard grass Y 2/2 plants monocots Poaceae Aristida polyclados C 1/1 plants monocots Poaceae Cymbopogon ambiguus lemon grass C 1/1 plants monocots Poaceae Digitaria ctenantha C 1/1 plants monocots Poaceae Enteropogon ramosus C 1/1 plants monocots Poaceae Enneapogon avenaceus C 1/1 plants monocots Poaceae Eragrostis tenellula delicate lovegrass C 2/2 plants monocots Poaceae Urochloa praetervisa C 1/1 plants monocots Poaceae Heteropogon contortus black speargrass C 1/1 plants monocots Poaceae Iseilema membranaceum small flinders grass C 1/1 plants monocots Poaceae Bothriochloa ewartiana desert bluegrass C 2/2 plants monocots Poaceae Brachyachne convergens common native couch C 2/2 plants monocots Poaceae Enneapogon lindleyanus C 3/3 plants monocots Poaceae Enneapogon polyphyllus leafy nineawn C 1/1 plants monocots Poaceae Sporobolus actinocladus katoora grass C 1/1 plants monocots Poaceae Cenchrus pennisetiformis Y 1/1 plants monocots Poaceae Sporobolus australasicus C 1/1 plants monocots Poaceae Eriachne pulchella subsp. dominii C 1/1 plants monocots Poaceae Dichanthium sericeum subsp. humilius C 1/1 plants monocots Poaceae Digitaria divaricatissima var. divaricatissima C 1/1 plants monocots Poaceae Eriachne mucronata forma (Alpha C.E.Hubbard 7882) C 1/1 plants monocots Poaceae Sehima nervosum C 1/1 plants monocots Poaceae Eulalia aurea silky browntop C 2/2 plants monocots Poaceae Chloris virgata feathertop rhodes grass Y 1/1 CODES I - Y indicates that the taxon is introduced to Queensland and has naturalised. -

Honey and Pollen Flora of SE Australia Species
List of families - genus/species Page Acanthaceae ........................................................................................................................................................................34 Avicennia marina grey mangrove 34 Aizoaceae ............................................................................................................................................................................... 35 Mesembryanthemum crystallinum ice plant 35 Alliaceae ................................................................................................................................................................................... 36 Allium cepa onions 36 Amaranthaceae ..................................................................................................................................................................37 Ptilotus species foxtails 37 Anacardiaceae ................................................................................................................................................................... 38 Schinus molle var areira pepper tree 38 Schinus terebinthifolius Brazilian pepper tree 39 Apiaceae .................................................................................................................................................................................. 40 Daucus carota carrot 40 Foeniculum vulgare fennel 41 Araliaceae ................................................................................................................................................................................42 -

Brisbane Native Plants by Suburb
INDEX - BRISBANE SUBURBS SPECIES LIST Acacia Ridge. ...........15 Chelmer ...................14 Hamilton. .................10 Mayne. .................25 Pullenvale............... 22 Toowong ....................46 Albion .......................25 Chermside West .11 Hawthorne................. 7 McDowall. ..............6 Torwood .....................47 Alderley ....................45 Clayfield ..................14 Heathwood.... 34. Meeandah.............. 2 Queensport ............32 Trinder Park ...............32 Algester.................... 15 Coopers Plains........32 Hemmant. .................32 Merthyr .................7 Annerley ...................32 Coorparoo ................3 Hendra. .................10 Middle Park .........19 Rainworth. ..............47 Underwood. ................41 Anstead ....................17 Corinda. ..................14 Herston ....................5 Milton ...................46 Ransome. ................32 Upper Brookfield .......23 Archerfield ...............32 Highgate Hill. ........43 Mitchelton ...........45 Red Hill.................... 43 Upper Mt gravatt. .......15 Ascot. .......................36 Darra .......................33 Hill End ..................45 Moggill. .................20 Richlands ................34 Ashgrove. ................26 Deagon ....................2 Holland Park........... 3 Moorooka. ............32 River Hills................ 19 Virginia ........................31 Aspley ......................31 Doboy ......................2 Morningside. .........3 Robertson ................42 Auchenflower -

Alphitonia Excelsa Common Name: Red Ash Family - Rhamnaceae
Alphitonia Excelsa Common Name: Red Ash Family - Rhamnaceae Description • Alphitonia Excelsa is a small to medium size tree with a branching canopy formation • Reaches a height of 15m and width of 6m • The tree is commonly found in dry sclerophyll forest and rainforests • Favours well drained soils and is highly suitable for erosion control areas • Fast growing ability, highly suitable for areas prone to coastal salty winds and drought condition • Prefers full sun conditions • Spectacular cream ‘petal-like’ flowers appear from summer to autumn • Ecological role provides a habitat for native birds (cockatoos) and the small green-banded blue butterfly • Round black fruit ripens from June to September • Distribution occurs from the coastal areas of WA across the top end of the NT, and along the coastline from Northern Qld to the southern coastal areas of NSW How to look after this plant • Prefers full sun • When planting tree into ground, dig a slow release native fertiliser (low phosphorous formulation) into soil to provide plant with essential nutrients, encourage healthy plant growth and increase flowering. Slow release fertiliser will generally last up to 6 months, reapply between 5-6 months to continue plant growth • Water every 2-3 days a week for the first month when planted. Cut back watering to once or twice a week after the first month (avoid over watering) • Lightly prune after the flowering season to increase the foliage growth • If soil is low in organic matter, dig compost into existing soil to develop valuable humus around your plant. • For clay soils, dig gypsum and garden soil into the existing ground to encourage drainage. -

Auwahi: Ethnobotany of a Hawaiian Dryland Forest
AUWAHI: ETHNOBOTANY OF A HAWAIIAN DRYLAND FOREST. A. C. Medeiros1, C.F. Davenport2, and C.G. Chimera1 1. U.S. Geological Survey, Biological Resources Division, Haleakala Field Station, P.O. Box 369, Makawao, HI 96768 2. Social Sciences Department, Maui Community College, 310 Ka’ahumanu Ave., Kahului, HI 96732 ABSTRACT Auwahi district on East Maui extends from sea level to about 6800 feet (1790 meters) elevation at the southwest rift of leeward Haleakal¯a volcano. In botanical references, Auwahi currently refers to a centrally located, fairly large (5400 acres) stand of diverse dry forest at 3000-5000 feet (915- 1525 meters) elevation surrounded by less diverse forest and more open-statured shrubland on lava. Auwahi contains high native tree diversity with 50 dryland species, many with extremely hard, durable, and heavy wood. To early Hawaiians, forests like Auwahi must have seemed an invaluable source of unique natural materials, especially the wide variety of woods for tool making for agriculture and fishing, canoe building, kapa making, and weapons. Of the 50 species of native trees at Auwahi, 19 species (38%) are known to have been used for medicine, 13 species (26%) for tool-making, 13 species (26%) for canoe building 13 species (26%) for house building, 8 species (16%) for tools for making kapa, 8 species (16%) for weapons 8 species (16%) for fishing, 8 species (16%) for dyes, and 7 species (14 %) for religious purposes. Other miscellaneous uses include edible fruits or seeds, bird lime, cordage, a fish narcotizing agent, firewood, a source of "fireworks", recreation, scenting agents, poi boards, and h¯olua sled construction. -

Alphitonia Excelsa
Plant of the Month - February by Allan Carr Alphitonia excelsa soap tree Pronunciation: al-fit-OWN-ee-a ek-SELL-sa RHAMNACEAE Derivation: Alphitonia, from the Greek, alphiton – baked barley meal (referring to the red mealy matter around the seeds); excelsa, from the Latin, excelsus – elevated, lofty (referring to its tall habit). Chewed leaves (undersides) Buds, flowers, sugar ant Fruits, both green and mature There are about 20 Alphitonia species, mostly in tropical areas around the world with 7 or 8 extending to Australia. Description: A. excelsa is a tree to 18 m, sometimes smaller, that occurs in deep sands on forest edges in coastal and near coastal areas from northern Qld down into southern NSW. It is also found in northern WA and NT The bark is usually distinctively mottled with a variety of lichens. Young parts of the plant are covered in rusty hairs and smell of sarsaparilla when crushed. The common name comes from the ability to form a soapy froth when leaves are rubbed with wet hands. This is due to a high *saponin content. Bark Leaves to 150 mm x 55 mm are alternate, green above with an under surface of silvery- white with fine hairs. Their edges are slightly curled under and frequently show much damage after being eaten by various leaf chewing insects including caterpillars of the Small Green-banded Blue butterfly (Psychonotis caelius). Flowers are creamy-green, tiny, 5-petalled and borne in *axillary clusters from November to April. Fruits are dry, black, globular to 12 mm across with reddish -brown seeds inside. -
Alphitonia Excelsa (A
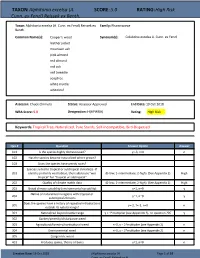
TAXON: Alphitonia excelsa (A. SCORE: 5.0 RATING: High Risk Cunn. ex Fenzl) Reissek ex Benth. Taxon: Alphitonia excelsa (A. Cunn. ex Fenzl) Reissek ex Family: Rhamnaceae Benth. Common Name(s): Cooper's wood Synonym(s): Colubrina excelsa A. Cunn. ex Fenzl leather jacket mountain ash pink almond red almond red ash red tweedie soaptree white myrtle whiteleaf Assessor: Chuck Chimera Status: Assessor Approved End Date: 19 Oct 2018 WRA Score: 5.0 Designation: H(HPWRA) Rating: High Risk Keywords: Tropical Tree, Naturalized, Pure Stands, Self-Incompatible, Bird-Dispersed Qsn # Question Answer Option Answer 101 Is the species highly domesticated? y=-3, n=0 n 102 Has the species become naturalized where grown? 103 Does the species have weedy races? Species suited to tropical or subtropical climate(s) - If 201 island is primarily wet habitat, then substitute "wet (0-low; 1-intermediate; 2-high) (See Appendix 2) High tropical" for "tropical or subtropical" 202 Quality of climate match data (0-low; 1-intermediate; 2-high) (See Appendix 2) High 203 Broad climate suitability (environmental versatility) y=1, n=0 y Native or naturalized in regions with tropical or 204 y=1, n=0 y subtropical climates Does the species have a history of repeated introductions 205 y=-2, ?=-1, n=0 n outside its natural range? 301 Naturalized beyond native range y = 1*multiplier (see Appendix 2), n= question 205 y 302 Garden/amenity/disturbance weed 303 Agricultural/forestry/horticultural weed n=0, y = 2*multiplier (see Appendix 2) n 304 Environmental weed n=0, y = 2*multiplier (see Appendix 2) n 305 Congeneric weed 401 Produces spines, thorns or burrs y=1, n=0 n Creation Date: 19 Oct 2018 (Alphitonia excelsa (A. -

Section 8-Maggie-Final AM
KEY TO GROUP 8 Shrubs or trees usually more than 1.5 m tall. A. flower B. phyllode and C. leaf D. leaf E. leaf margins F. leaf margins spike pod lobed dissected crenate serrate NOTE: The following trees and shrubs, which are deciduous when flowering, will not come out in this key unless you can find a leaf. There are usually some old ones on the ground or even a few hanging on the tree. These plants are: Brachychiton (Group 8.G), Cochlospermum (Group 8.G), Cordia (Group 8.K), Gyrocarpos (Group 8.G), Sterculia (Group 8.O), Terminalia (Group 8.M), Turraea (Group 8.R), and the mangrove, Xylocarpus (Group 1.H). 1 Leaves with oil glands, readily visible with a hand lens if not to the naked eye, aromatic when crushed, eucalypt or citrus smell. (Chiefly eucalypts, paperbarks, bottlebrushes and similar) go to 2 1* Leaves lacking easily seen oil glands, if aromatic when crushed, then smell not of an eucalypt; citrus or even an apple smell go to 5 Oil glands/dots as seen with a good hand lens 2 Trees; petals fused to form an operculum or cap, stamens numerous and free (eucalpyts) go to 3 2* Shrubs or trees, petals not fused to form an operculum or cap, stamens if numerous then usually united into bundles or stamens are fewer than 10 (Myrtaceae-Rutaceae) go to 4 3 Bark smooth throughout but occasionally some rough fibrous or persistent bark at base go to Group 8.A 3* Persistent, fibrous bark for at least 2-3 m or usually more from the base go to Group 8.B 4 Flowers clustered into spikes (see sketch A), old capsules usually remain on the old wood -

Nomenclatural Notes on the Alphitonia Group in Australia (Rhamnaceae) Jürgen Kellermanna,B
Swainsona 33: 135–142 (2020) © 2020 Board of the Botanic Gardens & State Herbarium (Adelaide, South Australia) Nomenclatural notes on the Alphitonia Group in Australia (Rhamnaceae) Jürgen Kellermanna,b a State Herbarium of South Australia, Botanic Gardens and State Herbarium, Hackney Road, Adelaide, South Australia 5000 Email: [email protected] b The University of Adelaide, School of Biological Sciences, Adelaide, South Australia 5005 Abstract: The nomenclature and typification of seven species of Alphitonia Reissek ex Endl. and Emmenosperma F.Muell. is discussed. These two genera form the “Alphitonia Group” together with Granitites Rye and Jaffrea H.C.Hopkins & Pillon from New Caledonia. Lectotypes are chosen for E. cunninghamii Benth. and for the synonyms A. excelsa var. acutifolia Braid, A. obtusifolia R.Br. ex Braid and A. obtusifolia var. tenuis Braid. The lectotypes of A. petriei Braid & C.T.White and A. philippinensis Braid are clarified. Three species are illustrated: A. petriei, A. whitei Braid and E. cunninghamii. Keywords: Nomenclature, typification, second-step lectotype, Rhamnaceae, incertae sedis, Australia Introduction when fruits are ripe, they split open and the pericarp falls off, leaving the seeds (usually 3) remaining attached Rhamnaceae Juss. is a medium-sized plant family with to the base of the fruit (Fig. 3F, P). over 1000 species in 64 genera. The current intra- familial classification was devised by Richardson et al. Alphitonia (10–15 species) was published in (2000b), following the first molecular analysis of the Endlicher (1840), using Reissek’s manuscript name whole family (Richardson et al. 2000a). The family is and description. He indicated that Colubrina excelsa divided into 11 tribes, but several genera have not been A.Cunn. -

Jewel Bugs of Australia (Insecta, Heteroptera, Scutelleridae)1
© Biologiezentrum Linz/Austria; download unter www.biologiezentrum.at Jewel Bugs of Australia (Insecta, Heteroptera, Scutelleridae)1 G. CASSIS & L. VANAGS Abstract: The Australian genera of the Scutelleridae are redescribed, with a species exemplar of the ma- le genitalia of each genus illustrated. Scanning electron micrographs are also provided for key non-ge- nitalic characters. The Australian jewel bug fauna comprises 13 genera and 25 species. Heissiphara is described as a new genus, for a single species, H. minuta nov.sp., from Western Australia. Calliscyta is restored as a valid genus, and removed from synonymy with Choerocoris. All the Australian species of Scutelleridae are described, and an identification key is given. Two new species of Choerocoris are des- cribed from eastern Australia: C. grossi nov.sp. and C. lattini nov.sp. Lampromicra aerea (DISTANT) is res- tored as a valid species, and removed from synonymy with L. senator (FABRICIUS). Calliphara nobilis (LIN- NAEUS) is recorded from Australia for the first time. Calliphara billardierii (FABRICIUS) and C. praslinia praslinia BREDDIN are removed from the Australian biota. The identity of Sphaerocoris subnotatus WAL- KER is unknown and is incertae sedis. A description is also given for the Neotropical species, Agonoso- ma trilineatum (FABRICIUS); a biological control agent recently introduced into Australia to control the pasture weed Bellyache Bush (Jatropha gossypifolia, Euphorbiaceae). Coleotichus borealis DISTANT and C. (Epicoleotichus) schultzei TAUEBER are synonymised with C. excellens (WALKER). Callidea erythrina WAL- KER is synonymized with Lampromicra senator. Lectotype designations are given for the following taxa: Coleotichus testaceus WALKER, Coleotichus excellens, Sphaerocoris circuliferus (WALKER), Callidea aureocinc- ta WALKER, Callidea collaris WALKER and Callidea curtula WALKER. -

Inventory of Vascular Plants of the Kahuku Addition, Hawai'i
CORE Metadata, citation and similar papers at core.ac.uk Provided by ScholarSpace at University of Hawai'i at Manoa PACIFIC COOPERATIVE STUDIES UNIT UNIVERSITY OF HAWAI`I AT MĀNOA David C. Duffy, Unit Leader Department of Botany 3190 Maile Way, St. John #408 Honolulu, Hawai’i 96822 Technical Report 157 INVENTORY OF VASCULAR PLANTS OF THE KAHUKU ADDITION, HAWAI`I VOLCANOES NATIONAL PARK June 2008 David M. Benitez1, Thomas Belfield1, Rhonda Loh2, Linda Pratt3 and Andrew D. Christie1 1 Pacific Cooperative Studies Unit (University of Hawai`i at Mānoa), Hawai`i Volcanoes National Park, Resources Management Division, PO Box 52, Hawai`i National Park, HI 96718 2 National Park Service, Hawai`i Volcanoes National Park, Resources Management Division, PO Box 52, Hawai`i National Park, HI 96718 3 U.S. Geological Survey, Pacific Island Ecosystems Research Center, PO Box 44, Hawai`i National Park, HI 96718 TABLE OF CONTENTS ABSTRACT.......................................................................................................................1 INTRODUCTION...............................................................................................................1 THE SURVEY AREA ........................................................................................................2 Recent History- Ranching and Resource Extraction .....................................................3 Recent History- Introduced Ungulates...........................................................................4 Climate ..........................................................................................................................4 -

PLANT SPECIES AVAILABLE from NOOSA & DISTRICT LANDCARE RESOURCE CENTRE, POMONA, September 2015 (Opposite the Pub)
PLANT SPECIES AVAILABLE FROM NOOSA & DISTRICT LANDCARE RESOURCE CENTRE, POMONA, September 2015 (opposite the pub) Prices: Tube stock: $2.00 * Orders 100-500: $1.80 Kauri, Brown & Hoop pines: $2.20 * Orders 500 plus: $1.54 Bunya pines: $3.50 * Orders over 1000 – price negotiable Specials: $1.00 * Larger pots as marked * Members receive 10% - 20% discount on plants * Phone 5485 2468 to pre-order plants Acacia fimbriata BRISBANE WATTLE Shrub or bushy small tree to 4m. Hardy and fast growing. Attractive ferny semi-weeping foliage. Flowers are scented yellow fluffy balls in winter. Acacia falcata SICKLE WATTLE Shrub to 4 m throughout Queensland and NSW, mostly in Coastal areas. Often very ‘showy’ flowering periods in June with cream coloured ball-flowers. Unusual seed pods show the seeds very obviously which attracts birds such as the pale headed rosellas. Alectryon coriaceus BEACH ALECTRYON Bushy coastal shrub 1-6m. Panicles of small yellow flowers in winter and distinctive bird-attracting fruit. Very hardy in a coastal site, not frost tolerant. Allocasuarina littoralis BLACK SHE-OAK Open forest tree to 10m, black fissured bark. Hardy, adaptable and fast growing in variety of sites. Black cockatoo feed tree, suitable for cabinet work. Allocasuarina torulosa ROSE SHE-OAK Medium tree slender and pyramidal 10 – 25 metres. Food tree for Black Cockatoos. Hardy and adaptable; suitable for moist rich or nutrient-deficient sandy soils; frost tolerant. Alpinia caerulea NATIVE GINGER Clumping plant to 1.5m. Understorey species, likes shady moist site. Bright blue berries attract birds. Fruit, leaves and tuberous roots are edible and make a tasty addition to salads.