DOCSLIB.ORG

Evidence of Exotic Meson Particle Discovered At

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Evidence of Exotic Meson Particle Discovered At Vol. 51 - No. 37 September 19, 1997 BROOKHAVEN NATIONAL LABORATORY Evidence of Exotic Meson Particle Discovered at AGS Researchers at BNL’s Alternating mass of 1.4 GeV after years of select- Gradient Synchrotron (AGS) accelera- ing and analyzing data from products tor have found evidence of a new and of billions of particle collisions made rare subatomic particle called an “ex- during the experiment’s 1994 run. otic” meson. The result was presented to par- This finding at AGS Experiment ticipants of the Seventh International 852, described in the September 1 Conference on Hadron Spectroscopy, issue of Physical Review Letters, helps held at BNL August 25-30 (see story validate the standard model, the cen- on page 2). At the conference, confir- tral theory of modern physics. mation of the E852 result was re- Also, the finding could improve un- ported by what is called the Crystal derstanding of how matter binds to- Barrel collaboration at CERN, the gether at the relatively low energy European particle physics laboratory. level of 18 billion electron volts (GeV). “In some sense, we’ve discovered a The E852 team of 51 scientists, new form of matter,” said Chung. “This graduate students and undergradu- particle had been hypothesized [in ates includes researchers from: BNL, the late 1970s], but it’s never, never Northwestern University, Rensselaer been pinned down. Polytechnic Institute, the University “To find evidence of a particle that of Massachusetts, Dartmouth College, has never been detected before, one and Russia’s Institute for High En- that’s so important to our understand- ergy Physics and the Moscow State ing of elementary particles, is hugely University. satisfying,” Chung continued. “Just The E852 collaboration also in- as satisfying is the fact that we found cludes an Indiana University group, it at the AGS, the home to so many which did not sign the Physical Re- particle discoveries over the decades view Letters publication. “Instead of a and, as our work also shows, a great short letter, the Indiana group wanted machine for high-energy physics.” to write a longer paper, with all the To do the experiment, E852 re- technical and experimental details searchers aimed an 18-GeV beam of included,” said Senior Physicist Suh- negatively charged pions from the Roger Stoutenburgh Urk Chung of BNL’s Physics Depart- AGS at a target of liquid hydrogen. ment, an E852 cospokesman. The target was in a device called a Funded by the U.S. Department of multi-particle spectrometer (MPS), an Energy (DOE) and the National Sci- instrument designed to detect many ence Foundation, the E852 research- different types of particles at once. ers uncovered an exotic meson with a (continued on page 2) At the Alternating Gradient Synchrotron, Experiment 852 researchers (from left, front, counterclockwise) Dennis Weygand, Hans Willutzki, Suh-Urk Chung and Robert Hackenburg are beside the multi-particle spectrometer with which the exotic meson was found. LIA Suports HFBR Review Process, Opposes D’Amato, Forbes Legislation Bromley Calls Anti-HFBR Bill The Board of Directors of the Long Island Association (LIA), the region’s largest business and civic organization, has unanimously passed a resolution ‘Unwise, Unwarranted’ urging that the U.S. Department of Energy be allowed to complete its process of In reaction to the bills introduced into the U.S. Congress by U.S. evaluating the environmental, safety, health and community impact of BNL’s Senator Alfonse D’Amato and Representative Michael Forbes, D. Allan High Flux Beam Reactor (HFBR) and then allowing Energy Secretary Federico Bromley, who is the past President of the American Physical Society and Peña to make a determination as to whether the reactor should be restarted. the former Director of the Office of Science & Technology Policy under Hence the LIA’s resolution opposes the legislation introduced into the U.S. President George Bush, sent them a letter, excerpted below, on Thursday Senate by Senator Alfonse D’Amato and into the House by U.S. Representative September 11, with copies to all members of the House and Senate energy Michael Forbes, which attempts to shut down the reactor permanently without & water development appropriations subcommittees. any evaluation through any process. Dear Senator D’Amato and Representative Forbes: “The decision on the future of Brookhaven National Laboratory’s reactor should be based on science, not politics,” noted LIA President Matthew Crosson On behalf of more than 40,000 physicists throughout the United in a press release issued on Monday, September 15. “To flatly require that the States, the Council of The American Physical Society last April adopted reactor never be reopened, regardless of findings which might determine a statement on neutron scattering facilities. That statement, a copy of otherwise, is unnessary and unwise. It also may be damaging to Long Island’s which I am enclosing, stresses the critical role that neutron science plays future economy. The facilities at the Laboratory, including the reactor, were core in a wide range of technologies across many fields. The statement also component’s of Project Long Island’s determination that Long Island’s future calls attention to the loss of American leadership in this area of research will largely depend on high technology industries.” and the risks that our nation will face if the problem is not soon Crosson continued, “The LIA will urge both houses of Congress to oppose the redressed. legislation introduced by Senator D’Amato and Congressman Forbes. This issue I have learned recently that you and Representative Michael Forbes is too important to Long Island and the country’s future scientific endeavors to have submitted companion legislation that would permanently close be determined by political considerations.” Brookhaven’s High Flux Beam Reactor, one of only four major neutron The LIA President concluded, “It is through research at [the HFBR] that we scattering facilities in our country. From a scientific standpoint, I believe may be able to find cures for Lyme disease, cancer, arthritis and heart disease. that such action is unwise and unwarranted. For almost half a century, Let’s not be so abrupt in our decision to shut out these possibilities. Long Island Brookhaven has been one of the gems in our nation’s scientific enter- deserves better than that.” prise, and the High Flux Beam Reactor has been an integral part of the Established in 1926 and now based in Commack, the LIA represents approxi- laboratory’s outstanding program. mately half of Nassau and Suffolk’s work force and aims to improve Long Island’s Sincerely, D. Allan Bromley business and working environment. Interim Director Announces Five Changes Within BNL’s Organization On Tuesday, September 16, BNL’s Noted Bond, “I want to thank Sue ment of new management systems ning Manager. Becoming Interim Re- Interim Director Peter Bond an- for her heroic efforts over the past and processes.” actor Division Manager is Al Queirolo, nounced that, effective that day, five several years, which were extremely Bill Gunther, who since 1994 has who since 1995 had been that changes had taken place within the stressful and challenging times for been the Manager of the Office of En- Division’s Deputy Manager. The Re- Lab’s interim organization. the Laboratory.” vironmental Restoration (OER), has actor Division operates both BNL’s First, at her request, Sue Davis He continued, “I am extremely been named Interim Associate Direc- High Flux Beam Reactor (HFBR) and stepped down as BNL’s Associate Di- pleased that Dr. Davis has agreed to tor for Reactor, Safety & Security. the Brookhaven Medical Research rector for Reactor, Safety & Security, serve as a senior advisor within the Replacing Gunther as Interim OER Reactor. the position that she has held since Director’s Office [because] her experi- Manager is Bob Howe, who until Tues- “I want to thank Dave for his con- 1992. Davis will remain within the ence and knowledge of the Laboratory’s day was OER’s Deputy Manager. tributions to both the HFBR and the Director’s Office, as a senior advisor ES&H programs and related issues In addition, Dave Rorer, the Man- Laboratory during a particularly diffi- on environment, safety and health will be invaluable as we pursue a ager of the Reactor Division since 1995, cult time at the HFBR,” commented (ES&H). change in our culture and the develop- is now that Division’s Strategic Plan- Bond. Brookhaven Bulletin September 19, 1997 in which they found confirmation of Hadron Spectroscopy ’97: An Exotic Event the new particle. Conference attendee Ted Barnes, The annual International Confer- Oak Ridge National Laboratory and ence on Hadron Spectroscopy has been University of Tennessee, who gave key in the field since its inception, the first plenary-session talk and is and the seventh such conference, held not affiliated with either the E852 or at BNL this year from August 25 to the Crystal Barrel collaborations, had 30, proved to be exceptionally excit- commented earlier on the finding. ing. “This is a very important discov- As the 194 scientists from 19 coun- ery,” Barnes said. “Theorists have pre- tries who attended the conference dicted the existence of exotic hybrid learned, not only had a long-sought- mesons, which contain both quarks after new particle, an exotic meson, and gluons, since the late 1970s, but finally been observed (see story on E852 may have found the smoking page 1), but also, using an entirely gun for their existence. It’s a bench- different approach, another experi- mark that will set the mathematical mental team had uncovered evidence scales for future experimentation and supporting the discovery. theoretical study.” First, the evidence for an exotic Michael Herbert Said Chung, “This could be the meson with a mass of 1.4 billion elec- beginning of a new era in hadron tron volts (GeV) found at Experiment spectroscopy, where multiquarks and 852 at BNL’s Alternating Gradient gluons are accepted as constituents of Synchrotron, was formally presented hadrons.
Load more

Recommended publications
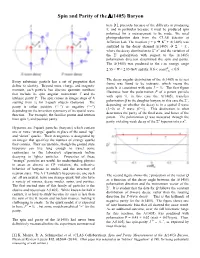
  • Spin and Parity of the Λ(1405) Baryon
    Spin and Parity of the (1405) Baryon here [1], precisely because of the difficulty in producing it, and in particular because it must be produced spin polarized for a measurement to be made. We used photoproduction data from the CLAS detector at Jefferson Lab. The reaction + p K+ + (1405) was analyzed in the decay channel (1405) + + , where the decay distribution to + and the variation of the + polarization with respect to the (1405) polarization direction determined the spin and parity. The (1405) was produced in the c.m. energy range K 2.55 < W < 2.85 GeV and for 0.6 coscm.. 0.9 . The decay angular distribution of the (1405) in its rest Every subatomic particle has a set of properties that frame was found to be isotropic, which means the define its identity. Beyond mass, charge, and magnetic particle is consistent with spin J = ½. The first figure moment, each particle has discrete quantum numbers illustrates how the polarization P of a parent particle that include its spin angular momentum J and its with spin ½, in this case the (1405), transfers intrinsic parity P. The spin comes in integer steps of ԰ + starting from ½ for 3-quark objects (baryons). The polarization Q to the daughter baryon, in this case the , depending on whether the decay is in a spatial S wave parity is either positive (“+”) or negative (“”) (L=0) or P wave (L=1). This distinction is what depending on the inversion symmetry of its spatial wave determines the parity of the final state, and hence of the function. For example, the familiar proton and neutron parent.
    [Show full text]
  • The Subatomic Particle Mass Spectrum
    The Subatomic Particle Mass Spectrum Robert L. Oldershaw 12 Emily Lane Amherst, MA 01002 USA [email protected] Key Words: Subatomic Particles; Particle Mass Spectrum; General Relativity; Kerr Metric; Discrete Self-Similarity; Discrete Scale Relativity 1 Abstract: Representative members of the subatomic particle mass spectrum in the 100 MeV to 7,000 MeV range are retrodicted to a first approximation using the Kerr solution of General Relativity. The particle masses appear to form a restricted set of quantized values of a Kerr- based angular momentum-mass relation: M = n1/2 M, where values of n are a set of discrete integers and M is a revised Planck mass. A fractal paradigm manifesting global discrete self- similarity is critical to a proper determination of M, which differs from the conventional Planck mass by a factor of roughly 1019. This exceedingly simple and generic mass equation retrodicts the masses of a representative set of 27 well-known particles with an average relative error of 1.6%. A more rigorous mass formula, which includes the total spin angular momentum rule of Quantum Mechanics, the canonical spin values of the particles, and the dimensionless rotational parameter of the Kerr angular momentum-mass relation, is able to retrodict the masses of the 8 dominant baryons in the 900 MeV to 1700 MeV range at the < 99.7% > level. 2 “There remains one especially unsatisfactory feature [of the Standard Model of particle physics]: the observed masses of the particles, m. There is no theory that adequately explains these numbers. We use the numbers in all our theories, but we do not understand them – what they are, or where they come from.
    [Show full text]
  • FUNDAMENTAL PARTICLES Year 14 Physics Erin Hannigan
    FUNDAMENTAL PARTICLES Year 14 Physics Erin Hannigan 1 Key Word List ■ Natural Philosophy – the science of matter and energy and their interactions. ■ Hadron – any elementary particle that interacts strongly with other particles. ■ Lepton – an elementary particle that participates in weak interactions. ■ Subatomic Particle – a body having finite mass and internal structure but negligible dimensions. ■ Quark – any of a number f subatomic particles carrying a fractional electric charge, postulated as building blocks of the hadrons. Quarks have not been directly observed but theoretical predictions based on their existence have been confirmed experimentally. ■ Atom – the smallest component of an element having the chemical properties of the element. 2 Fundamental Particles ■ Fundamental particles (also called elementary particles) are the smallest building blocks of the universe. The key characteristic of fundamental particles is that they have no internal structure. ■ There are two type of fundamental particles: – Particles that make up all matter, called fermions – Particles that carry force, called bosons ■ The four fundamental forces include: – Gravity – The weak force – Electromagnetism – The strong force 3 The Four Fundamental Forces ■ The four fundamental forces of nature govern everything that happens in the universe. ■ Gravity – The attraction between two objects that have mass or energy ■ The weak force – Responsible for particle decay – Physicists describe this interaction through the exchange of force-carrying particles called
    [Show full text]
  • Introduction to Subatomic- Particle Spectrometers∗
    IIT-CAPP-15/2 Introduction to Subatomic- Particle Spectrometers∗ Daniel M. Kaplan Illinois Institute of Technology Chicago, IL 60616 Charles E. Lane Drexel University Philadelphia, PA 19104 Kenneth S. Nelsony University of Virginia Charlottesville, VA 22901 Abstract An introductory review, suitable for the beginning student of high-energy physics or professionals from other fields who may desire familiarity with subatomic-particle detection techniques. Subatomic-particle fundamentals and the basics of particle in- teractions with matter are summarized, after which we review particle detectors. We conclude with three examples that illustrate the variety of subatomic-particle spectrom- eters and exemplify the combined use of several detection techniques to characterize interaction events more-or-less completely. arXiv:physics/9805026v3 [physics.ins-det] 17 Jul 2015 ∗To appear in the Wiley Encyclopedia of Electrical and Electronics Engineering. yNow at Johns Hopkins University Applied Physics Laboratory, Laurel, MD 20723. 1 Contents 1 Introduction 5 2 Overview of Subatomic Particles 5 2.1 Leptons, Hadrons, Gauge and Higgs Bosons . 5 2.2 Neutrinos . 6 2.3 Quarks . 8 3 Overview of Particle Detection 9 3.1 Position Measurement: Hodoscopes and Telescopes . 9 3.2 Momentum and Energy Measurement . 9 3.2.1 Magnetic Spectrometry . 9 3.2.2 Calorimeters . 10 3.3 Particle Identification . 10 3.3.1 Calorimetric Electron (and Photon) Identification . 10 3.3.2 Muon Identification . 11 3.3.3 Time of Flight and Ionization . 11 3.3.4 Cherenkov Detectors . 11 3.3.5 Transition-Radiation Detectors . 12 3.4 Neutrino Detection . 12 3.4.1 Reactor Neutrinos . 12 3.4.2 Detection of High Energy Neutrinos .
    [Show full text]
  • Qt7r7253zd.Pdf
    Lawrence Berkeley National Laboratory Recent Work Title RELATIVISTIC QUARK MODEL BASED ON THE VENEZIANO REPRESENTATION. II. GENERAL TRAJECTORIES Permalink https://escholarship.org/uc/item/7r7253zd Author Mandelstam, Stanley. Publication Date 1969-09-02 eScholarship.org Powered by the California Digital Library University of California Submitted to Physical Review UCRL- 19327 Preprint 7. z RELATIVISTIC QUARK MODEL BASED ON THE VENEZIANO REPRESENTATION. II. GENERAL TRAJECTORIES RECEIVED LAWRENCE RADIATION LABORATORY Stanley Mandeistam SEP25 1969 September 2, 1969 LIBRARY AND DOCUMENTS SECTiON AEC Contract No. W7405-eng-48 TWO-WEEK LOAN COPY 4 This is a Library Circulating Copy whIch may be borrowed for two weeks. for a personal retention copy, call Tech. Info. Dlvislon, Ext. 5545 I C.) LAWRENCE RADIATION LABORATOR SLJ-LJ UNIVERSITY of CALIFORNIA BERKELET DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California.
    [Show full text]
  • Hadrons and Nuclei Abstract
    Hadrons and Nuclei William Detmold (editor),1 Robert G. Edwards (editor),2 Jozef J. Dudek,2, 3 Michael Engelhardt,4 Huey-Wen Lin,5 Stefan Meinel,6, 7 Kostas Orginos,2, 3 and Phiala Shanahan1 (USQCD Collaboration) 1Massachusetts Institute of Technology 2Jefferson Lab 3College of William and Mary 4New Mexico State University 5Michigan State University 6University of Arizona 7RIKEN BNL Research Center Abstract This document is one of a series of whitepapers from the USQCD collaboration. Here, we discuss opportunities for lattice QCD calculations related to the structure and spectroscopy of hadrons and nuclei. An overview of recent lattice calculations of the structure of the proton and other hadrons is presented along with prospects for future extensions. Progress and prospects of hadronic spectroscopy and the study of resonances in the light, strange and heavy quark sectors is summarized. Finally, recent advances in the study of light nuclei from lattice QCD are addressed, and the scope of future investigations that are currently envisioned is outlined. 1 CONTENTS Executive summary3 I. Introduction3 II. Hadron Structure4 A. Charges, radii, electroweak form factors and polarizabilities4 B. Parton Distribution Functions5 1. Moments of Parton Distribution Functions6 2. Quasi-distributions and pseudo-distributions6 3. Good lattice cross sections7 4. Hadronic tensor methods8 C. Generalized Parton Distribution Functions8 D. Transverse momentum-dependent parton distributions9 E. Gluon aspects of hadron structure 11 III. Hadron Spectroscopy 13 A. Light hadron spectroscopy 14 B. Heavy quarks and the XYZ states 20 IV. Nuclear Spectroscopy, Interactions and Structure 21 A. Nuclear spectroscopy 22 B. Nuclear Structure 23 C. Nuclear interactions 26 D.
    [Show full text]
  • The Ghost Particle 1 Ask Students If They Can Think of Some Things They Cannot Directly See but They Know Exist
    Original broadcast: February 21, 2006 BEFORE WATCHING The Ghost Particle 1 Ask students if they can think of some things they cannot directly see but they know exist. Have them provide examples and reasoning for PROGRAM OVERVIEW how they know these things exist. NOVA explores the 70–year struggle so (Some examples and evidence of their existence include: [bacteria and virus- far to understand the most elusive of all es—illnesses], [energy—heat from the elementary particles, the neutrino. sun], [magnetism—effect on a com- pass], and [gravity—objects falling The program: towards Earth].) How do scientists • relates how the neutrino first came to be theorized by physicist observe and measure things that cannot be seen with the naked eye? Wolfgang Pauli in 1930. (They use instruments such as • notes the challenge of studying a particle with no electric charge. microscopes and telescopes, and • describes the first experiment that confirmed the existence of the they look at how unseen things neutrino in 1956. affect other objects.) • recounts how scientists came to believe that neutrinos—which are 2 Review the structure of an atom, produced during radioactive decay—would also be involved in including protons, neutrons, and nuclear fusion, a process suspected as the fuel source for the sun. electrons. Ask students what they know about subatomic particles, • tells how theoretician John Bahcall and chemist Ray Davis began i.e., any of the various units of mat- studying neutrinos to better understand how stars shine—Bahcall ter below the size of an atom. To created the first mathematical model predicting the sun’s solar help students better understand the neutrino production and Davis designed an experiment to measure size of some subatomic particles, solar neutrinos.
    [Show full text]
  • Chiral Extrapolations and Exotic Meson Spectrum
    Physics Letters B 526 (2002) 72–78 www.elsevier.com/locate/npe Chiral extrapolations and exotic meson spectrum Anthony W. Thomas a, Adam P. Szczepaniak b a Special Research Centre for the Subatomic Structure of Matter and Department of Physics and Mathematical Physics, Adelaide University, Adelaide SA 5005, Australia b Department of Physics and Nuclear Theory Center, Indiana University, Bloomington, IN 47405, USA Received 15 June 2001; received in revised form 10 December 2001; accepted 18 December 2001 Editor: H. Georgi Abstract We examine the chiral corrections to exotic meson masses calculated in lattice QCD. In the soft pion limit we find that corrections from virtual, closed channels lead to strong non-linear behavior which has been found in other hadronic systems. We find the resulting mass shifts to be as large as 100 MeV and therefore large corrections to the predictions of exotic meson masses based on linear extrapolations to the chiral limit are expected. Furthermore, by considering a class of phenomenologically successful hybrid meson models we show that this behavior is not altered by contributions from open decay channels. 2002 Published by Elsevier Science B.V. One of the biggest challenges in hadronic physics is with glueballs—they have regular quantum numbers to understand the role of gluonic degrees of freedom. and therefore cannot be unambiguously identified as Even though there is evidence from high energy purely gluonic excitations. On the other hand, the ex- experiments that gluons contribute significantly to istence of mesons with exotic quantum numbers (com- hadron structure, for example, to the momentum and binations of spin, parity and charge conjugation, J PC, spin sum rules, there is a pressing need for direct which cannot be attributed to valence quarks alone), observation of gluonic excitations at low energies.
    [Show full text]
  • Make an Atom Vocabulary Grade Levels
    MAKE AN ATOM Fundamental to physical science is a basic understanding of the atom. Atoms are comprised of protons, neutrons, and electrons. Protons and neutrons are at the center of the atom while electrons live in lobe-shaped clouds outside the nucleus. The number of electrons usually matches the number of protons, yielding a net neutral charge for the atom. Sometimes an atom has less neutrons or more neutrons than protons. This is called an isotope. If an atom has different numbers of electrons than protons, then it is an ion. If an atom has different numbers of protons, it is a different element all together. Scientists at Idaho National Laboratory study, create, and use radioactive isotopes like Uranium 234. The 234 means this isotope has an atomic mass of 234 Atomic Mass Units (AMU). GRADE LEVELS: 3-8 VOCABULARY Atom – The basic unit of a chemical element. Proton – A stable subatomic particle occurring in all atomic nuclei, with a positive electric charge equal in magnitude to that of an electron, but of opposite sign. Neutron – A subatomic particle of about the same mass as a proton but without an electric charge, present in all atomic nuclei except those of ordinary hydrogen. Electron – A stable subatomic particle with a charge of negative electricity, found in all atoms and acting as the primary carrier of electricity in solids. Orbital – Each of the actual or potential patterns of electron density that may be formed on an atom or molecule by one or more electrons. Ion – An atom or molecule with a net electric charge due to the loss or gain of one or more electrons.
    [Show full text]
  • LINE SHAPES of the EXOTIC C¯C MESONS X(3872)
    LINE SHAPES OF THE EXOTIC cc¯ MESONS X(3872) AND Z±(4430) DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Meng Lu, B.S., M.S. ***** The Ohio State University 2008 Dissertation Committee: Approved by Eric Braaten, Adviser Richard J. Furnstahl Adviser Klaus Honscheid Graduate Program in Junko Shigemitsu Physics c Copyright by Meng Lu 2008 ABSTRACT The B-factory experiments have recently discovered a series of new cc¯ mesons, including the X(3872) and the first manifestly exotic meson Z±(4430). The prox- 0 0 imity of the mass of the X to the D∗ D¯ threshold has motivated its identification as a loosely-bound hadronic molecule whose constituents are a superposition of the 0 0 0 0 charm mesons pairs D∗ D¯ and D D¯ ∗ . Factorization formulas for its line shapes are derived by taking advantage of the universality of S-wave resonances near a 2-particle threshold and by including the effects from the nonzero width of D∗ meson and the inelastic scattering channels of the charm mesons. The best fit to the line shapes of + 0 0 0 X in the J/ψπ π− and D D¯ π channels measured by the Belle Collaboration corre- 0 0 sponds to the X being a bound state whose mass is just below the D∗ D¯ threshold. The differences between the line shapes of X produced in B+ decays and B0 decays as + + 0 0 0 0 well as in decay channels J/ψπ π−,J/ψπ π−π , and D D¯ π are further derived by taking into account the effects from the closeby channel composed of charged charm mesons.
    [Show full text]
  • Chiral Extrapolations and Exotic Meson Spectrum
    IUNTC 01-02 ADP-01-18/T453 May 2001 CHIRAL EXTRAPOLATIONS AND EXOTIC MESON SPECTRUM Anthony W. Thomasa and Adam P. Szczepaniakb a Special Research Centre for the Subatomic Structure of Matter and Department of Physics and Mathematical Physics, Adelaide University, Adelaide SA 5005, Australia a Department of Physics and Nuclear Theory Center Indiana University, Bloomington, IN 47405, USA We examine the chiral corrections to exotic meson masses calculated in lattice QCD. In particular, we ask whether the non-linear chiral behavior at small quark masses, which has been found in other hadronic systems, could lead to large cor- rections to the predictions of exotic meson masses based on linear extrapolations to the chiral limit. We find that our present understanding of exotic meson decay dy- namics suggests that open channels may not make a significant contribution to such non-linearities whereas the virtual, closed channels may be important. arXiv:hep-ph/0106080v1 7 Jun 2001 1. Introduction. One of the biggest challenges in hadronic physics is to understand the role of gluonic degrees of freedom. Even though there is evidence from high energy experiments that gluons contribute significantly to hadron structure, for example to the momentum and spin sum rules, there is a pressing need for direct observation of gluonic excitations at low energies. In particular, it is expected that glue should manifest itself in the meson spectrum and reflect on the nature of confinement. In recent years a few candidates for glueballs and hybrid mesons have been re- ported. For example, there are two major glueball candidates, the f0(1500) and f0(1710), scalar-isoscalar mesons observed inpp ¯ annihilation, in central production as well as in J/ψ (f0(1710)) decays [1].
    [Show full text]
  • Classification of Elementary Particles
    CLASSIFICATION OF ELEMENTARY PARTICLES #Classification On the basis of “SPIN”: - •Elementary Particles are categorised in two classes i.e. Bosons and Fermions: - BOSONS Introduction: In particle physics boson is the type of particle that obeys the rule of Bose- Einstein statistics. These bosons have quantum spin having integral value 0, +1, -1, +2, -2, etc. •History: The name Boson comes from the surname of Indian physicist Satyendra Nath Bose and physicist Albert Einstein. They develop a method of analysis called Bose-Einstein Statistics. In an effort to understand the Plank's law, Bose proposed a method to analyse the behaviour of photon in 1924.He sent paper to Einstein. One of the most dramatic effect of Bose- Einstein Statistics is the prediction that boson can overlap and coexist with other bosons. Because of this it is possible to become a photon to laser. The name Boson First coined by scientists Paul Dirac in the honour of famous scientists Satyendra Nath Bose and Albert Einstein. Regarding: •Boson are fundamental particle such as gluons ,W ,Z boson, recently discovered Higgs boson aka God particle and Graviton. •Boson may be elementary like Photon or Composite i.e.made with two or more elementary particle. •All observed particles are either fermion or Boson. Types of Bosons- •Bosons are categorised into two categories; Gauge Boson: Gauge Boson are the particle that Carries the interaction of fundamental forces between particles. All known Gauge Boson have spin 1 and therefore all Gauge Boson are vector. •gauge boson is characterized into 5 categories. •Gluons(g): That carries strong nuclear forces between matter particle.
    [Show full text]