And Doberman Pinscher Strategy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

WIEZE 2018.Pdf
Dogshow der Hopstreek CAC Wieze 39 Ste K.V.N tentoonstelling Oktoberhallen, Schroverstraat te Wieze (op 4km van Aalst) info: [email protected] Secretariaat: Impens Bianca 0032 (0) 478 32 99 64 Titels: Hopprins(es) - Hopkoning(in) - Hopkeizer(in) 1 Prijs/1 Prix - 1 Sluiting/1 Fermeture Geen extra kosten - Pas de frais extra Klassen – Classes: Puppy – Chiot (6 – 9 m.) € 35 Minor puppy € 35 Jeugd – Jeune – Jugend – Youth (9 – 18 m.) € 49 Intermediaire – Intermediaire – Zwischen – Intermediate (15 – 24 m.) € 49 Open – Ouverte – Offene (>= 15 m.) € 49 Gebruik – Travail – Gebrauch – Utility (>= 15 m. + certificaat) € 49 Kampioen – Champion – Sieger (>= 15 m. + certificaat) € 49 Veteraan (Min 8 jaar – ans – Jahre – years) € 35 Vanaf de tweede hond € 45 - (uitgezonderd Baby, Puppy en Veteraan ) A partir du 2ième chien € 45-(Sauf pour les Baby, Puppy et Véteran) Abzug ab 2. Hund € 45 - (Außer für den Baby, Puppy oder Veteraan) Discount from 2nd dog € 45 - (Except for the Baby, Puppy or Veteran) Korting lid KVN – € 3 / hond - (per hond – par chien – pro hund – per dog) Koppels - Groepen GRATIS Sluiting - Fermeture 30 April 2018 Geen benches aanwezig – pas de cages – keine Benches– no benche Enkel online beveiligde betaling -Seulement inscription en ligne avec paiement sécurisé - Only online entry with secure payement www.doglle.com IBAN FR76 3004 7141 3100 0200 2880 337 – BIC CMCIFRPP Wieze Internationale CAC Hondententoonstelling- 39ste K.V.N. Show der Hopstreek 19-05-2018 & 20-05-2018 Zaterdag - Samedi 19-05-2018 : 1--4--5--6--9 Keurmeester/Juge -

Dog Breeds Pack 1 Professional Vector Graphics Page 1
DOG BREEDS PACK 1 PROFESSIONAL VECTOR GRAPHICS PAGE 1 Affenpinscher Afghan Hound Aidi Airedale Terrier Akbash Akita Inu Alano Español Alaskan Klee Kai Alaskan Malamute Alpine Dachsbracke American American American American Akita American Bulldog Cocker Spaniel Eskimo Dog Foxhound American American Mastiff American Pit American American Hairless Terrier Bull Terrier Staffordshire Terrier Water Spaniel Anatolian Anglo-Français Appenzeller Shepherd Dog de Petite Vénerie Sennenhund Ariege Pointer Ariegeois COPYRIGHT (c) 2013 FOLIEN.DS. ALL RIGHTS RESERVED. WWW.VECTORART.AT DOG BREEDS PACK 1 PROFESSIONAL VECTOR GRAPHICS PAGE 2 Armant Armenian Artois Hound Australian Australian Kelpie Gampr dog Cattle Dog Australian Australian Australian Stumpy Australian Terrier Austrian Black Shepherd Silky Terrier Tail Cattle Dog and Tan Hound Austrian Pinscher Azawakh Bakharwal Dog Barbet Basenji Basque Basset Artésien Basset Bleu Basset Fauve Basset Griffon Shepherd Dog Normand de Gascogne de Bretagne Vendeen, Petit Basset Griffon Bavarian Mountain Vendéen, Grand Basset Hound Hound Beagle Beagle-Harrier COPYRIGHT (c) 2013 FOLIEN.DS. ALL RIGHTS RESERVED. WWW.VECTORART.AT DOG BREEDS PACK 2 PROFESSIONAL VECTOR GRAPHICS PAGE 3 Belgian Shepherd Belgian Shepherd Bearded Collie Beauceron Bedlington Terrier (Tervuren) Dog (Groenendael) Belgian Shepherd Belgian Shepherd Bergamasco Dog (Laekenois) Dog (Malinois) Shepherd Berger Blanc Suisse Berger Picard Bernese Mountain Black and Berner Laufhund Dog Bichon Frisé Billy Tan Coonhound Black and Tan Black Norwegian -

IN RAKVERE 17Th & 18Th of October 2020
TWO NATIONAL ALL BREEDS DRIVE IN DOG SHOWS th th IN RAKVERE 17 & 18 of October 2020 Indoor Show will take place in RAKVERE SPORTSHALL, KASTANI 12 RAKVERE, ESTONIA Judging starts at 10 These double national shows are held under the protection of the Estonian Kennel Union. Dogs in intermediate, open, working and champion class compete for the Estonian CAC. Certificate (CAC) winning dog becomes an Estonian champion if the dog is a champion in its own country. Dogs in junior class (9-18 month) compete for the Estonian Junior Certificate – EST JUN CAC and for the Estonian Junior Champion title. Dogs in veteran class compete for the Estonian veteran certificate – EST VET CAC and for the Estonian Veteran Champion title. Organizer: RAKVERE KOERTESÕPRADE KLUBI INFO: by phone +372 521 9294 Maire Tõnurist CLASSES: /The decisive date concerning the age is the day of the show/ Babypuppy (4-6 month) BOB BABY BABY BIS Puppy (6-9 month) BOB PUPPY PUPPY BIS All dogs (except baby and puppy) Junior (9-18 month) compete for JUN-CAC BOB JUN JUN BIS in junior, intermediate, Intermediate (15-24 month) open, working, champion Open (from 15 month) Compete and veteran class Working (from 15 month) enclose the working certificate for CAC can compete for BOB, BIG Champion (from 15 month) enclose the champion title Veteran (from 8 year) VET CACEST VET CH title + BOB VET VET BIS and Best In Show ! ADDITIONAL COMPETITIONS: All dogs in competitions must be at least 9 month old and take part from this show and get also at least „very good“ from breed judging to take part at these additional competitions (except breeding dog himself in progeny class) Brace competition - for a male and a female dog of the same breed owned by the same owner. -

EPC Exhibit 134-10 May 20, 2011 the LIBRARY of CONGRESS
EPC Exhibit 134-10 May 20, 2011 THE LIBRARY OF CONGRESS Dewey Section To: Caroline Kent, Chair Decimal Classification Editorial Policy Committee Cc: Members of the Decimal Classification Editorial Policy Committee Karl E. Debus-López, Chief, U.S. General Division From: Giles Martin, Assistant Editor Winton Matthews, Consulting Assistant Editor Dewey Decimal Classification OCLC Online Computer Library Center, Inc Re: 636.72-636.76 Dog breeds Magdalena Svanberg, of the Kungliga biblioteket/National Library of Sweden, pointed out that the arrangement of dog breeds in 636.72-636.76 was different from that used by the Féderation Cynologique Internationale (FCI). The FCI classification is found at http://www.fci.be/nomenclature.aspx, and at the top level is: Group 1 Sheepdogs and Cattle Dogs (except Swiss Cattle Dogs) Group 2 Pinscher and Schnauzer - Molossoid Breeds - Swiss Mountain and Cattle Dogs Group 3 Terriers Group 4 Dachshunds Group 5 Spitz and Primitive types Group 6 Scenthounds and Related Breeds Group 7 Pointing Dogs Group 8 Retrievers - Flushing Dogs - Water Dogs Group 9 Companion and Toy Dogs Group 10 Sighthounds 1 The American Kennel Club (AKC) arrangement, followed by Dewey, is very different at the top level: Sporting Group 636.752 Hound Group 636.753 Working Group 636.73 Terrier Group 636.755 Toy Group 636.76 Non-Sporting Group 636.72 Herding Group 636.737 Miscellaneous Class (breeds which have not yet been put into the other groups) (The order given here is that on the AKC’s webpage, http://www.akc.org/breeds/index.cfm?nav_area=breeds ) The situation is made more complex because 636.72-636.76 contain several references to breeds as “(United Kingdom)” as a shortcut for saying that this group is one of the groupings of the Kennel Club of the United Kingdom (KC). -

Alphabetic Breedslist 12/08/201 2018 SHOW DOG
Alphabetic Breedslist 12/08/2018 - WORLD DOG SHOW 2018 Count Breed Cat.Nrs. Ring 35 II Affenpinscher 9721-9755 11 128 V Akita 13888-14015 44 Bis 105 V Alaskan Malamute 12845-12949 42 Bis 82 V American Akita 14016-14097 43 b 9 II Anatolian Shepherd Dog 11882-11890 22 b 25 II Appenzell Cattle Dog 12421-12445 26 2 II Austrian Pinscher 9756-9757 32 Bis 95 V Basenji 14508-14602 47 83 II Bernese Mountain Dog - Males 12446-12528 3 91 II Bernese Mountain Dog - Females 12529-12619 4 80 IX Bichon Frise 14894-14973 63 b 42 IX Bolognese 14974-15015 65 8 II Bosnian-Herzegovinian Croation Shepherd Dog 11918-11925 10 153 IX Boston Terrier 17467-17619 54 111 II Boxer 10677-10787 18 24 II Broholmer 10653-10676 51 a 107 II Bulldog - Males 11318-11424 17 97 II Bulldog - Females 11425-11521 20 102 II Bullmastiff 11522-11623 6 4 V Canaan Dog 14294-14297 51 a 7 V CANADIAN ESKIMO DOG 12707-12713 42 3 V Canarian Warren Hound 14603-14605 42 33 II Caucasian Shepherd Dog 12312-12344 8 110 IX Cavalier King Charles Spaniel 16545-16654 74 9 II Central Asia Shepherd Dog 12345-12353 22 b 70 IX Chihuahua long-Haired - Females 16475-16544 56 91 IX Chihuahua long-Haired - Males 16384-16474 55 68 IX Chihuahua Smooth-haired - Males 16240-16307 53 76 IX Chihuahua Smooth-haired - Females 16308-16383 52 78 IX Chinese Crested Dog - Females 15783-15860 50 77 IX Chinese Crested Dog - Males 15706-15782 51 b 65 V Chow Chow 13767-13831 38 7 II Cinmarrón Uruguaya 11891-11897 35 25 V Cirneco dell'Etna 14641-14665 36 a 115 IX Continental Toy Spaniel, Papillon 16799-16913 67 16 IX Continental -
Domestic Dog Breeding Has Been Practiced for Centuries Across the a History of Dog Breeding Entire Globe
ANCESTRY GREY WOLF TAYMYR WOLF OF THE DOMESTIC DOG: Domestic dog breeding has been practiced for centuries across the A history of dog breeding entire globe. Ancestor wolves, primarily the Grey Wolf and Taymyr Wolf, evolved, migrated, and bred into local breeds specific to areas from ancient wolves to of certain countries. Local breeds, differentiated by the process of evolution an migration with little human intervention, bred into basal present pedigrees breeds. Humans then began to focus these breeds into specified BREED Basal breed, no further breeding Relation by selective Relation by selective BREED Basal breed, additional breeding pedigrees, and over time, became the modern breeds you see Direct Relation breeding breeding through BREED Alive migration BREED Subsequent breed, no further breeding Additional Relation BREED Extinct Relation by Migration BREED Subsequent breed, additional breeding around the world today. This ancestral tree charts the structure from wolf to modern breeds showing overlapping connections between Asia Australia Africa Eurasia Europe North America Central/ South Source: www.pbs.org America evolution, wolf migration, and peoples’ migration. WOLVES & CANIDS ANCIENT BREEDS BASAL BREEDS MODERN BREEDS Predate history 3000-1000 BC 1-1900 AD 1901-PRESENT S G O D N A I L A R T S U A L KELPIE Source: sciencemag.org A C Many iterations of dingo-type dogs have been found in the aborigine cave paintings of Australia. However, many O of the uniquely Australian breeds were created by the L migration of European dogs by way of their owners. STUMPY TAIL CATTLE DOG Because of this, many Australian dogs are more closely related to European breeds than any original Australian breeds. -
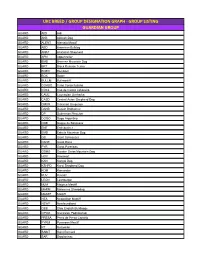
Ukc Breed / Group Designation Graph
UKC BREED / GROUP DESIGNATION GRAPH - GROUP LISTING GUARDIAN GROUP GUARD AIDI Aidi GUARD AKB Akbash Dog GUARD ALENT Alentejo Mastiff GUARD ABD American Bulldog GUARD ANAT Anatolian Shepherd GUARD APN Appenzeller GUARD BMD Bernese Mountain Dog GUARD BRT Black Russian Terrier GUARD BOER Boerboel GUARD BOX Boxer GUARD BULLM Bullmastiff GUARD CORSO Cane Corso Italiano GUARD CDCL Cao de Castro Laboreiro GUARD CAUC Caucasian Ovcharka GUARD CASD Central Asian Shepherd Dog GUARD CMUR Cimarron Uruguayo GUARD DANB Danish Broholmer GUARD DP Doberman Pinscher GUARD DOGO Dogo Argentino GUARD DDB Dogue de Bordeaux GUARD ENT Entlebucher GUARD EMD Estrela Mountain Dog GUARD GS Giant Schnauzer GUARD DANE Great Dane GUARD PYR Great Pyrenees GUARD GSMD Greater Swiss Mountain Dog GUARD HOV Hovawart GUARD KAN Kangal Dog GUARD KSHPD Karst Shepherd Dog GUARD KOM Komondor GUARD KUV Kuvasz GUARD LEON Leonberger GUARD MJM Majorca Mastiff GUARD MARM Maremma Sheepdog GUARD MASTF Mastiff GUARD NEA Neapolitan Mastiff GUARD NEWF Newfoundland GUARD OEB Olde English Bulldogge GUARD OPOD Owczarek Podhalanski GUARD PRESA Perro de Presa Canario GUARD PYRM Pyrenean Mastiff GUARD RT Rottweiler GUARD SAINT Saint Bernard GUARD SAR Sarplaninac GUARD SC Slovak Cuvac GUARD SMAST Spanish Mastiff GUARD SSCH Standard Schnauzer GUARD TM Tibetan Mastiff GUARD TJAK Tornjak GUARD TOSA Tosa Ken SCENTHOUND GROUP SCENT AD Alpine Dachsbracke SCENT B&T American Black & Tan Coonhound SCENT AF American Foxhound SCENT ALH American Leopard Hound SCENT AFVP Anglo-Francais de Petite Venerie SCENT -

AUSTRALIAN NATIONAL KENNEL COUNCIL LTD Judge
AUSTRALIAN NATIONAL KENNEL COUNCIL LTD GROUP 1 - TOYS Judge: Affenpinscher Bourbonnais Pointing Dog * Dachshund (Min. Long) Australian Silky Terrier Bracco Italiano Dachshund (Rabbit Long Bichon Frise Brittany Haired) * Bolognese * Chesapeake Bay Retriever Dachshund (Smooth) Cavalier King Charles Spaniel Clumber Spaniel Dachshund (Min. Smooth) Chihuahua (Long Coat) Cocker Spaniel Dachshund (Rabbit Smooth Chihuahua (Smooth Coat) Cocker Spaniel (American) Haired) * Chinese Crested Dog Curly Coated Retriever Dachshund (Wire) Continental Toy Spaniel Deutch Stichelhaar * Dachshund (Min. Wire) (Papillon) Drentsche Partridge Dog * Dachshund (Rabbit Wire Continental Toy Spaniel English Setter Haired) * (Phalene) * English Springer Spaniel Deerhound Coton De Tulear Field Spaniel Drever * Griffon Belge * Flat Coated Retriever Fawn Brittany Griffon * English Toy Terrier (Black & French Pointing Dog Gascogne Finnish Hound * Tan) Type * Finnish Spitz Griffon Bruxellois French Pointing Dog Pyrenean Foxhound Havanese Type * Gascon Saintongeois * Italian Greyhound French Spaniel * German Hound * Japanese Chin French Water Dog * Grand Basset Griffon King Charles Spaniel Frisian Pointing Dog * Vendeen Kromforhlander * Frisian Water Dog * Grand Griffon Vendeen * Lowchen German Shorthaired Pointer Great Anglo French-White & Maltese German Wirehaired Pointer Black Hound * Miniature Pinscher German Spaniel * Great Anglo-French Tri Colour Hound * Pekingese Golden Retriever Great Anglo-French White & Petit Brabancon * Gordon Setter Orange Hound * Pomeranian -

Judges Schedule Holland Cup 9Th December 2016
JUDGES SCHEDULE HOLLAND CUP 9TH DECEMBER 2016 FCI group 1 FCI group 6 , Panos Demetriou (CY): Berger Picard, Catalan Sheepdog, Ciobanesc Romanesc Gabriela Ridarčíková (SK): Rhodesian Ridgeback Carpatin, Ciobanesc Romanesc Mioritic, Croatian Sheepdog, Czeslovakian Wolfdog, Theo Viets (NL): Artésien-Norman Basset, Austrian Black And Tan Hound, Basset Dutch Shepherd Dog (all hair varieties), German Shepherd Dog, Long-Haired and Hound, Bavarian Mountain Scenthound, Beagle, Bernese Hound, Billy, Black and Tan Short-Haired, Komondor, Lancashire Heeler, Majorca Shepherd Dog, Maremma And Coonhound, Bleu Gascony Basset, Bloodhound, Dalmatian, Fawn Brittany Basset, Abruzzes Sheepdog, Mudi, Portuguese Sheepdog, Pyrenean Sheepdog, Long-Haired Finnish Hound, German Hound, Grand Basset griffon vendéen, Jura Hound, Lucerne and Smooth-Faces, South Russian Ovcharka Hound, Montenegrin Mountain Dog, Norwegian Hound, Otterhound, Petit Basset Rachel Dijkhorst-Noij (NL): Collie Rough, Collie Smooth, Old English Sheepdog, griffon vendéen, Polish Hound, Polish Hunting Dog, Schwyz Hound, Slovakian Hound, Shetland Sheepdog Small Blue Gascony Hound, Spanish Hound, Swedish Dachsbracke + all not Val Geddes (GB): Border Collie mentioned breeds of group 6 Jan de Gids (NL): Beauceron, Welsh Corgi Pembroke, White Swiss Shepherd Dog Svend Løvenkjær (DK): Australian Cattle Dog, Australian Kelpie, Australian Stumpy FCI group 7 , Tail Cattle Dog, Belgian Shepherd Dog, Groenendael, Laekenois, Malinois and Rudy Feyaerts (BE): Hungarian (Short-Haired and Wire-Haired) Pointing -

Kurzform Rasse / Abbreviation Breed Stand/As Of: Sept
Kurzform Rasse / Abbreviation Breed Stand/as of: Sept. 2016 A AP Affenpinscher / Monkey Terrier AH Afghanischer Windhund / Afgan Hound AID Atlas Berghund / Atlas Mountain Dog (Aidi) AT Airedale Terrier AK Akita AM Alaskan Malamute DBR Alpenländische Dachsbracke / Alpine Basset Hound AA American Akita ACS American Cocker Spaniel / American Cocker Spaniel AFH Amerikanischer Fuchshund / American Foxhound AST American Staffordshire Terrier AWS Amerikanischer Wasserspaniel / American Water Spaniel AFPV Small French English Hound (Anglo-francais de petite venerie) APPS Appenzeller Sennenhund / Appenzell Mountain Dog ARIE Ariegeois / Arigie Hound ACD Australischer Treibhund / Australian Cattledog KELP Australian Kelpie ASH Australian Shepherd SILT Australian Silky Terrier STCD Australian Stumpy Tail Cattle Dog AUST Australischer Terrier / Australian Terrier AZ Azawakh B BARB Franzosicher Wasserhund / French Water Dog (Barbet) BAR Barsoi / Russian Wolfhound (Borzoi) BAJI Basenji BAN Basst Artesien Normad / Norman Artesien Basset (Basset artesien normand) BBG Blauer Basset der Gascogne / Bue Cascony Basset (Basset bleu de Gascogne) BFB Tawny Brittany Basset (Basset fauve de Bretagne) BASH Basset Hound BGS Bayrischer Gebirgsschweisshund / Bavarian Mountain Hound BG Beagle BH Beagle Harrier BC Bearded Collie BET Bedlington Terrier BBS Weisser Schweizer Schäferhund / White Swiss Shepherd Dog (Berger Blanc Suisse) BBC Beauceron (Berger de Beauce) BBR Briard (Berger de Brie) BPIC Picardieschäferhund / Picardy Shepdog (Berger de Picardie (Berger Picard)) -

Breed Specific Instructions (BSI) Regarding Exaggerations in Pedigree Dogs
By the Nordic Kennel Clubs 2014 Applicable from 2014 Breed Specific Instructions (BSI) regarding exaggerations in pedigree dogs DANSK KENNEL KLUB HUNDARÆKTARFÉLAG ÍSLANDS NORSK KENNEL KLUB SUOMEN KENNELLIITTO SVENSKA KENNELKLUBBEN Index Introduction .............................................................................................................................4 Application ..............................................................................................................................6 Basics for all dogs ...................................................................................................................8 Breed types ...........................................................................................................................10 FCI GROUP 1 Sheepdogs and Cattle Dogs ..............................................................................12 FCI GROUP 2 Pinscher and Schnauzer - Molossoïd Breeds - Swiss Mountain and Cattle Dogs ...14 FCI GROUP 3 Terriers .............................................................................................................19 FCI GROUP 4 Dachshunds ......................................................................................................21 FCI GROUP 5 Spitz and Primitive types ...................................................................................22 FCI GROUP 6 Scenthounds and Related Breeds ......................................................................24 FCI GROUP 7 Pointing Dogs ....................................................................................................26 -

Breed Specific Instructions (BSI) Regarding Exaggerations in Pedigree Dogs
By the Nordic Kennel Clubs 2014 Applicable from 2014 Breed Specific Instructions (BSI) regarding exaggerations in pedigree dogs DANSK KENNEL KLUB HUNDARÆKTARFÉLAG ÍSLANDS NORSK KENNEL KLUB SUOMEN KENNELLIITTO SVENSKA KENNELKLUBBEN Index Introduction .............................................................................................................................4 Application ..............................................................................................................................6 Basics for all dogs ...................................................................................................................8 Breed types ...........................................................................................................................10 FCI GROUP 1 Sheepdogs and Cattle Dogs ..............................................................................12 FCI GROUP 2 Pinscher and Schnauzer - Molossoïd Breeds - Swiss Mountain and Cattle Dogs ...14 FCI GROUP 3 Terriers .............................................................................................................19 FCI GROUP 4 Dachshunds ......................................................................................................21 FCI GROUP 5 Spitz and Primitive types ...................................................................................22 FCI GROUP 6 Scenthounds and Related Breeds ......................................................................24 FCI GROUP 7 Pointing Dogs ....................................................................................................26