Super-Human Performance in Gran Turismo Sport Using Deep Reinforcement Learning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
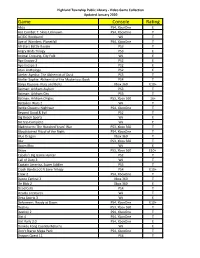
Game Console Rating
Highland Township Public Library - Video Game Collection Updated January 2020 Game Console Rating Abzu PS4, XboxOne E Ace Combat 7: Skies Unknown PS4, XboxOne T AC/DC Rockband Wii T Age of Wonders: Planetfall PS4, XboxOne T All-Stars Battle Royale PS3 T Angry Birds Trilogy PS3 E Animal Crossing, City Folk Wii E Ape Escape 2 PS2 E Ape Escape 3 PS2 E Atari Anthology PS2 E Atelier Ayesha: The Alchemist of Dusk PS3 T Atelier Sophie: Alchemist of the Mysterious Book PS4 T Banjo Kazooie- Nuts and Bolts Xbox 360 E10+ Batman: Arkham Asylum PS3 T Batman: Arkham City PS3 T Batman: Arkham Origins PS3, Xbox 360 16+ Battalion Wars 2 Wii T Battle Chasers: Nightwar PS4, XboxOne T Beyond Good & Evil PS2 T Big Beach Sports Wii E Bit Trip Complete Wii E Bladestorm: The Hundred Years' War PS3, Xbox 360 T Bloodstained Ritual of the Night PS4, XboxOne T Blue Dragon Xbox 360 T Blur PS3, Xbox 360 T Boom Blox Wii E Brave PS3, Xbox 360 E10+ Cabela's Big Game Hunter PS2 T Call of Duty 3 Wii T Captain America, Super Soldier PS3 T Crash Bandicoot N Sane Trilogy PS4 E10+ Crew 2 PS4, XboxOne T Dance Central 3 Xbox 360 T De Blob 2 Xbox 360 E Dead Cells PS4 T Deadly Creatures Wii T Deca Sports 3 Wii E Deformers: Ready at Dawn PS4, XboxOne E10+ Destiny PS3, Xbox 360 T Destiny 2 PS4, XboxOne T Dirt 4 PS4, XboxOne T Dirt Rally 2.0 PS4, XboxOne E Donkey Kong Country Returns Wii E Don't Starve Mega Pack PS4, XboxOne T Dragon Quest 11 PS4 T Highland Township Public Library - Video Game Collection Updated January 2020 Game Console Rating Dragon Quest Builders PS4 E10+ Dragon -

Course Organization CISC 877 Video Game Development Week 1: Introduction
Course Organization CISC 877 Video Game Development Week 1: Introduction T.C. Nicholas Graham [email protected] http://equis.cs.queensu.ca/wiki/index.php/CISC_877 Winter term, 2010 equis: engineering interactive systems Topics include… Timeline and Marking Scheme Video game design Gaminggp platforms and fundamental technolo gies Activity Due Date Grade January 26, Game development processes and pipeline Project Proposal (2-3 pages, hand-in) 10% 2010 Software architecture of video games Progress Presentation (involves Mar 2, 2010 20% Video games as distributed systems presentation and online report) Game physics Informal progress reports Weekly 5% GAIGame AI April 6, 2010 Scripting languages Final Project Presentation / Show 10% (tentative) Game development tools Final Project Report April 9, 2010 45% Social and ethical aspects of video games Class Participation 10% User in terf aces of gam es equis: engineering interactive systems equis: engineering interactive systems Homework Project proposal (for next week) Wiki contains detailed description of project ideas, game you will be extending The Project Proposal to be posted on Wiki – create yourself an account Form your own project groups – pick project appropriate to group size OGRE tutorials (over next two weeks) …see Wiki for details Download URL: http://equis.cs.queensu.ca/~graham/cisc877/soft/ equis: engineering interactive systems equis: engineering interactive systems The Game: Life is a Village The Game: Life is a Village Goal is to build an interesting village -

Magisterarbeit / Master's Thesis
MAGISTERARBEIT / MASTER’S THESIS Titel der Magisterarbeit / Title of the Master‘s Thesis „Player Characters in Plattform-exklusiven Videospielen“ verfasst von / submitted by Christof Strauss Bakk.phil. BA BA MA angestrebter akademischer Grad / in partial fulfilment of the requirements for the degree of Magister der Philosophie (Mag. phil.) Wien, 2019 / Vienna 2019 Studienkennzahl lt. Studienblatt / UA 066 841 degree programme code as it appears on the student record sheet: Studienrichtung lt. Studienblatt / Magisterstudium Publizistik- und degree programme as it appears on Kommunikationswissenschaft the student record sheet: Betreut von / Supervisor: tit. Univ. Prof. Dr. Wolfgang Duchkowitsch 1. Einleitung ....................................................................................................................... 1 2. Was ist ein Videospiel .................................................................................................... 2 3. Videospiele in der Kommunikationswissenschaft............................................................ 3 4. Methodik ........................................................................................................................ 7 5. Videospiel-Genres .........................................................................................................10 6. Geschichte der Videospiele ...........................................................................................13 6.1. Die Anfänge der Videospiele ..................................................................................13 -

Michelin to Make Playstation's Gran
PRESS INFORMATION NEW YORK, Aug. 23, 2019 — PlayStation has selected Michelin as “official tire technology partner” for its Gran Turismo franchise, the best and most authentic driving game, the companies announced today at the PlayStation Theater on Broadway. Under the multi-year agreement, Michelin also becomes “official tire supplier” of FIA Certified Gran Turismo Championships, with Michelin-branded tires featured in the game during its third World Tour live event also in progress at PlayStation Theater throughout the weekend. The relationship begins by increasing Michelin’s visibility through free downloadable content on Gran Turismo Sport available to users by October 2019. The Michelin-themed download will feature for the first time: . A new Michelin section on the Gran Turismo Sport “Brand Central” virtual museum, which introduces players to Michelin’s deep history in global motorsports, performance and innovation. Tire technology by Michelin available in the “Tuning” section of Gran Turismo Sport, applicable to the game’s established hard, medium and soft formats. On-track branding elements and scenography from many of the world’s most celebrated motorsports competitions and venues. In 1895, the Michelin brothers entered a purpose-built car in the Paris-Bordeaux-Paris motor race to prove the performance of air-filled tires. Since that storied race, Michelin has achieved a record of innovation and ultra-high performance in the most demanding and celebrated racing competitions around the world, including 22 consecutive overall wins at the iconic 24 Hours of Le Mans and more than 330 FIA World Rally Championship victories. Through racing series such as FIA World Endurance Championship, FIA World Rally Championship, FIA Formula E and International Motor Sports Association series in the U.S., Michelin uses motorsports as a laboratory to collect vast amounts of real-world data that power its industry-leading models and simulators for tire development. -

Printing from Playstation® 2 / Gran Turismo 4
Printing from PlayStation® 2 / Gran Turismo 4 NOTE: • Photographs can be taken within the replay of Arcade races and Gran Turismo Mode. • Transferring picture data to the printer can be via a USB lead between each device or USB storage media (Sony Computer Entertainment Australia Pty Ltd recommends the Sony Micro Vault ™) • Photographs can only be taken in SINGLE PLAYER mode. Photographs in Gran Turismo Mode Section 1. Taking Photo - Photo Travel (refer Gran Turismo Instruction Manual – Photo Travel) In the Gran Turismo Mode main screen go to Photo Travel (this is in the upper left corner of the map). Select your city, configure the camera angle, settings, take your photo and save your photo. Section 2. Taking Photo – Replay Theatre (refer Gran Turismo Instruction Manual) In the Gran Turismo Mode main scre en go to Replay Theatre (this is in the bottom right of the map). Choose the Replay file. Choose Play. The Replay will start. Press the Select during the replay when you would like to photograph the race. This will take you into Photo Shoot . Configure the camera angle, settings, take your photo and save your photo. Section 3. Printing a Photo – Photo Lab (refer Gran Turismo Instruction Manual) Connect the Epson printer to one of the USB ports on your PlayStation 2. Make sure there is paper in the printer. In the Gran Turismo Mode main screen select Home. Go to the Photo Lab. Go to Photo (selected from the left side). Select the photos you want to print. Choose the Print Icon ( the small printer shaped on the right-hand side of the screen) this will add the selected photos to the Print Folder. -

Ps4 Architecture
PS4 ARCHITECTURE JERRY AFFRICOT OVERVIEW • Evolution of game consoles • PlayStation History • CPU Architecture • GPU architecture • System Memory • Future of the PlayStation EVOLUTION OF GAME CONSOLES • 1967 • First video game console with two attached controllers • Invented by Ralph Baer • Only six simple games: ping-pong, tennis, handball, volleyball, chase games, light-gun games • 1975-1977 • Magnavox Odyssey consoles • Same games with better graphics, controllers. EVOLUTION OF GAME CONSOLES (continued) • 1978-1980 • First Nintendo video gaming consoles • First color TV game series sold only in Japan • 1981-1985 • Development of games like fighting, platform, adventure and RPG • Classic games: • Pac-man, Mario Bros, the Legend of Zelda etc. EVOLUTION OF GAMES CONSOLES (continued) • 1986-1990 • Mega Drive/Genesis • Super Nintendo Entertainment System (SNES) • 1991-1993 • Compact discs • Transition of 2D graphics to that of 3D graphics • First CD console launched by Philips (1991) EVOLUTION OF GAME CONSOLES (continued) • 1994-1997 • PlayStation release • Nintendo 64 (still using cartridges) • 1998-2004 • PlayStation 2 • GameCube • Xbox featuring Xbox Live HISTORY OF THE PLAYSTATION • PlayStation (1994) • PS1 (2000) • Smaller version of the PlayStation • PS2 (2000) • Backward compatible with most PS1 games • PS2 Slim line (2004) • Smaller version of the PS2 HISTORY OF THE PLAYSTATION (continued) • PSP (2004) • PS3 (2006) • First console to introduce use of motion sensing technology • Slimmer model released in 2009 • PSP Go (2009) • PS -

A Beginners Guide to SUPER GT IT’S AWESOME! Introduction to SUPER GT
A Beginners Guide to SUPER GT IT’S AWESOME! Introduction to SUPER GT UPER GT is the Japan's ■Full of world-class star drivers and team directors in SUPER GT premier touring car series S Drivers participating in SUPER GT are well be ranked among the world top featuring heavily-modified drivers. Many of them started their career from junior karting competitions, production cars (and cars that eventually stepped up into higher racing categories. Just as with baseball and are scheduled to be commercially football, SUPER GT has many world-class talents from both home and abroad. available). GT stands for Grand Furthermore, most teams appoint former drivers to team directors who have Touring - a high-performance car that is capable of high speed and achieved successful career in the top categories including Formula One and long-distance driving. SUPER GT is the 24 Hours of Le Mans. This has made the series establish a leading position a long-distance competition driven in the Japanese motor racing, creating even more exciting and dramatic battles by a couple of drivers per team to attracts millions of fans globally. sharing driving duties. The top class GT500 has undergone a big ■You don’t want to miss intense championship battles! transformation with new cars and regulations. The year 2014 is an In SUPER GT, each car is driven by two inaugural season in which the basic drivers sharing driving duties. Driver technical regulations is unified with points are awarded to the top ten the German touring car series DTM finishers in each race, and the driver duo (Deutsche Tourenwagen Masters). -

Personalized Game Reviews Information Systems and Computer
Personalized Game Reviews Miguel Pacheco de Melo Flores Ribeiro Thesis to obtain the Master of Science Degree in Information Systems and Computer Engineering Supervisor: Prof. Carlos Ant´onioRoque Martinho Examination Committee Chairperson: Prof. Lu´ısManuel Antunes Veiga Supervisor: Prof. Carlos Ant´onioRoque Martinho Member of the Committee: Prof. Jo~aoMiguel de Sousa de Assis Dias May 2019 Acknowledgments I would like to thank my parents and brother for their love and friendship through all my life. I would also like to thank my grandparents, uncles and cousins for their understanding and support throughout all these years. Moreover, I would like to acknowledge my dissertation supervisors Prof. Carlos Ant´onioRoque Martinho and Prof. Layla Hirsh Mart´ınezfor their insight, support and sharing of knowledge that has made this Thesis possible. Last but not least, to my girlfriend and all my friends that helped me grow as a person and were always there for me during the good and bad times in my life. Thank you. To each and every one of you, thank you. Abstract Nowadays one way of subjective evaluation of games is through game reviews. These are critical analysis, aiming to give information about the quality of the games. While the experience of playing a game is inherently personal and different for each player, current approaches to the evaluation of this experience do not take into account the individual characteristics of each player. We firmly believe game review scores should take into account the personality of the player. To verify this, we created a game review system, using multiple machine learning algorithms, to give multiple reviews for different personalities which allow us to give a more holistic perspective of a review score, based on multiple and distinct players' profiles. -

The New BMW 3 Series Gran Turismo. Contents
BMW Media information The new BMW 3 Series Gran Turismo. 02/2013 Contents. Page 1 1. The new BMW 3 Series Gran Turismo. Highlights. .................................................................................................................................. 2 2. Concept: Aesthetic appeal, space and functionality. ......................................................................6 3. Design: Innovative, emotional and practical. ...................................................................................7 4. Powertrain and chassis: Driving pleasure, dynamic excellence and comfort over long and short distances. ..................................................................................................................... 15 5. BMW EfficientDynamics: More power, less fuel consumption. ............................................................................. 22 6. BMW ConnectedDrive: Setting the pace for safety, convenience and infotainment. ................................ 26 7. Production: Optimised processes for uncompromising quality. ................................................. 29 7. Technical specifications. .............................................................................................. 30 8. Output and torque diagrams. ..................................................................................... 34 9. Exterior and interior dimensions. ............................................................................ 39 BMW Media information 1. The new BMW 3 Series Gran Turismo. 02/2013 -

Gran Turismo™ Sport ©2017 Sony Interactive Entertainment Inc
Gran Turismo™ Sport ©2017 Sony Interactive Entertainment Inc. Published by Sony Interactive Entertainment Europe. Developed by Polyphony Digital Inc. “Polyphony Digital logo”, “Gran Turismo” and “GT” are trademarks of Sony Interactive Entertainment Inc.. “ ”, “PlayStation”, “DUALSHOCK”, “ ” and “ ” are registered trademarks or trademarks of Sony Interactive Entertainment Inc. “Sony” is a registered trademark of Sony Corporation. All rights reserved. All titles, content, publisher names, trademarks, artwork, and associated imagery are trademarks and/or copyright material of their respective owners. Game/console/ PS4™ Vertical Stand not included. PlayStation®Plus 12 month subscription offer is available upon purchase of: XZ2, XZ2 Compact and and XZ Premium from 5th April 2018 to 30th June 2018. To participate and claim your PlayStation®Plus subscription you must access this offer via Xperia Lounge. All claims for PlayStation®Plus subscription must be made by 27 July 2018. Available in UK & Ireland. For full T&Cs please visit xperiaplaystationplus.co.uk. Use of Remote Play requires a PS4™ system, DUALSHOCK®4 wireless controller, Sony Entertainment Network account and high-speed internet connection with upload and download speeds of at least 15 Mbps. Use of your home WiFi is recommended. Some games do not support Remote Play. PlayStation®Plus subscription only available to Sony Entertainment Network (SEN) account holders with access to PlayStation®Store and high-speed internet. PlayStation™Network (PSN), PS Store and PS Plus subject to terms of use and country and language restrictions; PS Plus content and services vary by subscriber age. Users must be 7 years or older and users under 18 require parental consent. Service availability is not guaranteed. -

Ps4 Game Saves Download Gran Turismo Ps4 Game Saves Download Gran Turismo
ps4 game saves download gran turismo Ps4 game saves download gran turismo. PS4 Game Name: Gran Turismo 4 Working on: CFW 5.05 ISO Region: USA Language: English Game Source: DVD Game Format: PKG Mirrors Available: Rapidgator. Gran Turismo 4 (USA) PS4 ISO Download Links https://filecrypt.cc/Container/9240F74495.html. So, what do you think ? You must be logged in to post a comment. Search. About. Welcome to PS4 ISO Net! Our goal is to give you an easy access to complete PS4 Games in PKG format that can be played on your Jailbroken (Currently Firmware 5.05) console. All of our games are hosted on rapidgator.net, so please purchase a premium account on one of our links to get full access to all the games. If you find any broken link, please leave a comment on the respective game page and we will fix it as soon as possible. Ps4 game saves download gran turismo. Downloads: 212,814 Categories: 237. Total Download Views: 91,654,153. Total Files Served: 7,337,307. Total Size Served: 53.21 TB. Gran Turismo 6 Starter Save File. Download Name: Gran Turismo 6 Starter Save File NEW. Date Added: Mon. Aug 02, 2021. File Size: 92.27 KB. File Type: (Zip file) I made this modded savefile on GT6 which makes the game start with 50.000 credits and the starter Honda Fit. I wanted to create a save with a small credit bonus to compensate a bit for the lack of seasonal events, but didnt want to ruin the game experience and make progress meaningless. -

STS 145 Game Review: Wipeout
STS 145 Game Review: Wipeout Game Review: Wipeout Yu Ping Hu <[email protected]> 22 February 2001 The Sport of the Future In 2052, anti-gravity racing is all the rage. The F3600 Race League boasts the best anti-grav race craft, the finest pilots, and the fastest action. This is the world Psygnosis created for Wipeout, one of the first games available for the Playstation after the console's 1995 launch. In the first half of the twenty-first century, scientists were developing anti-grav technology. However, due to corporate greed and political maneuvering, government support of this research disappeared, and the researchers ridiculed. Despite this, anti-grav was a total success, solving the world's fuel and transportation problems, and giving rise to what would become the most popular sport of all time. To be honest, the story line for Wipeout is thin, supplied in two pages of "quotes" in the game manual. However, it doesn't matter: it's simply a pretext for high speed racing. Once you start the game, all that matters is flying faster than the other 7 racers, and finishing the three-lap race in first place. This is no mean feat: every race, you start in last place, and need to speed your way to the front of the pack. They apparently don't believe in pole position in 2052. Full credits and publication information are also available. Gameplay Basics The game offers three modes: single race, time trial, and championship race. Single race allows you to play against computer controlled opponents on any of the tracks, while time trial allows you to fly solo against the clock.