DOCSLIB.ORG

15-853:Algorithms in the Real World Cryptography Outline Public Key

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
15-853:Algorithms in the Real World Cryptography Outline Public Key Cryptography Outline Introduction: terminology, cryptanalysis, security 15-853:Algorithms in the Real World Primitives: one-way functions, trapdoors, … Protocols: digital signatures, key exchange, .. Cryptography 3 and 4 Number Theory: groups, fields, … Private-Key Algorithms: Rijndael, DES Public-Key Algorithms: – Diffie-Hellman Key Exchange – El-Gamal, RSA, Blum-Goldwasser – Quantum Cryptography Case Studies: Kerberos, Digital Cash 15-853 Page 1 15-853 Page 2 Public Key Cryptosystems One-way trapdoor functions Introduced by Diffie and Hellman in 1976. Both Public-Key and Digital signatures make use of one-way trapdoor functions. Plaintext Public Key systems Public Key: K = public key 1 K1 Encryption Ek(M) = C – Encode: c = f(m) K2 = private key – Decode: m = f-1(c) using trapdoor Cyphertext Digital signatures Digital Signatures: K Decryption D (C) = M – Sign: c = f-1(m) using trapdoor 2 k K1 = private key – Verify: m = f(c) K2 = public key Original Plaintext Typically used as part of a more complicated protocol. 15-853 Page 3 15-853 Page 4 1 Example of TLS (previously SSL) Public Key History TLS (Transport Layer Security) is the standard for the web (https), and voice over IP. Some algorithms Protocol (somewhat simplified): Bob -> amazon.com – Diffie-Hellman, 1976, key-exchange based on discrete logs B->A: client hello: protocol version, acceptable ciphers – Merkle-Hellman, 1978, based on “knapsack problem” A->B: server hello: cipher, session ID, |amazon.com|verisign – McEliece, 1978, based on algebraic coding theory hand- B->A: key exchange, {masterkey} – RSA, 1978, based on factoring amazon’s public key shake A->B: server finish: ([amazon,prev-messages,masterkey])key1 – Rabin, 1979, security can be reduced to factoring B->A: client finish: ([bob,prev-messages,masterkey])key2 – ElGamal, 1985, based on discrete logs A->B: server message: (message1,[message1])key1 data – Blum-Goldwasser, 1985, based on quadratic residues B->A: client message: (message2,[message2]) key2 – Elliptic curves, 1985, discrete logs over Elliptic curves |h| = Certificate issuer – Chor-Rivest, 1988, based on knapsack problem = Issuer, <h,h’s public key, time stamp> issuer’s private key – NTRU, 1996, based on Lattices <…>private key = Digital signature {…}public key = Public-key encryption – XTR, 2000, based on discrete logs of a particular field [..] = Secure Hash (…)key = Private-key encryption key1 and key2 are derived from masterkey and session ID 15-853 Page 5 15-853 Page 6 Diffie-Hellman Key Exchange Person-in-the-middle attack A group (G,*) and a primitive element (generator) g is made public. – Alice picks a, and sends ga to Bob ga gc – Bob picks b and sends gb to Alice Alice – The shared key is gab Mallory Bob Note the shared key is easy for Alice or Bob to gd gb compute, but assuming discrete logs are hard is Key = gad Key = gcb hard for anyone else to compute. 1 1 Can someone see a problem with this protocol? Mallory gets to listen to everything. 15-853 Page 7 15-853 Page 8 2 ElGamal ElGamal Public-key Cryptosystem Based on the difficulty of the discrete log problem. (G,*) is a group Encode: Invented in 1985 • α a generator for G Pick random k ∈ Z|G| Digital signature and Key-exchange variants • a ∈ Z E(m) = (y1, y2) – Digital signature is AES standard |G| = (α k, m * βk) • β = αa – Public Key used by TRW (avoided RSA patent) G is selected so that it Decode: Works over various groups a -1 is hard to solve the D(y) = y2 * (y1 ) k ka -1 – Zp, discrete log problem. = (m * β ) * (α ) – Multiplicative group GF(pn), = m * βk * (βk)-1 = m – Elliptic Curves Public Key: (α, β) and some description of G You need to know a to Private Key: a easily decode y! 15-853 Page 9 15-853 Page 10 ElGamal: Example Merkle-Hellman Gets “security” from the Subet Sum (also called * Encode: 7 G = Z11 knapsack) which is NP-hard to solve in general. Pick random k = 4 • α = 2 Subset Sum (Knapsack): Given a sequence W = {w ,w , E(m) = (24, 7 * 34) 0 1 • a = 8 …,w }, w ∈ Z of weights and a sum S, calculate a = (5, 6) n-1 i • β = 28 (mod 11) = 3 boolean vector B, such that: Decode: (5, 6) 8 -1 D(y) = 6 * (5 ) = 6 * 4-1 = 6 * 3 (mod 11) * = 7 Even deciding if there is a solution is NP-hard. Public Key: (2, 3), Z11 Private Key: a = 8 15-853 Page 11 15-853 Page 12 3 Merkle-Hellman Merkle-Hellman W is superincreasing if: What we need Encode: n y = E(m) = ∑i=1 mi w’i It is easy to solve the subset-sum problem for • w1, , wn superincreasing superincreasing W in O(n) time. Decode: integers Main idea of Merkle-Hellman: z = a-1 y mod p n • p > ∑i=1 wi and prime -1 n – Hide the easy case by multiplying each w by a = a ∑i=1 mi w’i mod p i • a, 1 ≤ a ≤ n -1 n constant a modulo a prime p = a ∑i=1 miaiwi mod p • w’ = a w mod p n i i = ∑i=1 mi wi – Knowing a and p allows you to retrieve the Solve subset sum prob: Public Key: w’i superincreasing sequence (w1, , wn, z) Private Key: wi, p, a, obtaining m1, mn 15-853 Page 13 15-853 Page 14 RSA Merkle Hellman: Problem Name after Rivest, Shamir and Adleman (1978) but Was broken by Shamir in 1984. apparently invented by Clifford Cocks in 1973. Shamir showed how to use integer programming to Based on difficulty of factoring. * solve the particular class of Subset Sum problems Used to hide the size of a group Zn since: in polynomial time. Factoring has not been reduced to RSA Lesson: don’t leave your trapdoor loose. – an algorithm that generates m from c does not give an efficient algorithm for factoring On the other hand, factoring has been reduced to finding the private-key. – there is an efficient algorithm for factoring given one that can find the private key from the public key. 15-853 Page 15 15-853 Page 16 4 RSA Public-key Cryptosystem RSA continued Why it works: What we need: Public Key: (e,n) D(c) = cd mod n • p and q, primes of Private Key: d = med mod n approximately the 1 + k(p-1)(q-1) same size Encode: = m mod n = m1 + k φ(n) mod n • n = pq m ∈ Zn φ(n) = (p-1)(q-1) E(m) = me mod n = m(m φ(n))k mod n * • e ∈ Z φ(n) = m • d = e-1 mod φ(n) Why is this argument not quite sound? Decode: * φ(n) d What if m ∉ Zn then m ≠ 1 mod n D(c) = c mod n Answer 1: Not hard to show that it still works. Answer 2: jackpot – you’ve factored n 15-853 Page 17 15-853 Page 18 RSA computations Security of RSA To generate the keys, we need to Warning: – Find two primes p and q. Generate candidates – Do not use this or any other algorithm naively! and use primality testing to filter them. Possible security holes: – Find e-1 mod (p-1)(q-1). Use Euclid’s – Need to use “safe” primes p and q. In particular algorithm. Takes time log2(n) p-1 and q-1 should have large prime factors. To encode and decode – p and q should not have the same number of digits. – Take me or cd. Use the power method. Can use a middle attack starting at sqrt(n). Takes time log(e) log2(n) and log(d) log2(n) . – e cannot be too small In practice e is selected to be small so that encoding – Don’t use same n for different e’s. is fast. – You should always “pad” 15-853 Page 19 15-853 Page 20 5 Algorithm to factor given d and e RSA Performance If an attacker has an algorithm that generates d Performance: (600Mhz PIII) (from: ssh toolkit): from e, then he/she can factor n in PPT. Variant Algorithm Bits/key Mbits/sec of the Rabin-Miller primality test. 1024 .35sec/key RSA Keygen Function TryFactor(e,d,n) LasVegas algorithm 2048 2.83sec/key 1. write ed – 1 as 2sr, r odd Probability of pass 1024 1786/sec 3.5 RSA Encrypt 2. choose w at random < n is > .5. 2048 672/sec 1.2 r 3. v = w mod n Will return p or q 1024 74/sec .074 4. if v = 1 then return(fail) RSA Decrypt if it passes. 2048 12/sec .024 5. while v ≠ 1 mod n Try until you pass. ElGamal Enc. 1024 31/sec .031 6. v = v 0 ElGamal Dec. 1024 61/sec .061 7. v = v2 mod n DES-cbc 56 95 8. if v0 = n - 1 then return(fail) twofish-cbc 128 140 9. return(pass, gcd(v0 + 1, n)) Rijndael 128 180 15-853 Page 21 15-853 Page 22 RSA in the “Real World” Factoring in the Real World Part of many standards: PKCS, ITU X.509, Quadratic Sieve (QS): ANSI X9.31, IEEE P1363 Used by: SSL, PEM, PGP, Entrust, … – Used in 1994 to factor a 129 digit (428-bit) number. 1600 Machines, 8 months. The standards specify many details on the implementation, e.g. Number field Sieve (NFS): – e should be selected to be small, but not too small – Used in 1999 to factor 155 digit (512-bit) number. – “multi prime” versions make use of n = pqr… 35 CPU years.
Load more

Recommended publications
  • Bilinear Map Cryptography from Progressively Weaker Assumptions
    Full version of an extended abstract published in Proceedings of CT-RSA 2013, Springer-Verlag, Feb. 2013. Available from the IACR Cryptology ePrint Archive as Report 2012/687. The k-BDH Assumption Family: Bilinear Map Cryptography from Progressively Weaker Assumptions Karyn Benson, Hovav Shacham ∗ Brent Watersy University of California, San Diego University of Texas at Austin fkbenson, [email protected] [email protected] February 4, 2013 Abstract Over the past decade bilinear maps have been used to build a large variety of cryptosystems. In addition to new functionality, we have concurrently seen the emergence of many strong assump- tions. In this work, we explore how to build bilinear map cryptosystems under progressively weaker assumptions. We propose k-BDH, a new family of progressively weaker assumptions that generalizes the de- cisional bilinear Diffie-Hellman (DBDH) assumption. We give evidence in the generic group model that each assumption in our family is strictly weaker than the assumptions before it. DBDH has been used for proving many schemes secure, notably identity-based and functional encryption schemes; we expect that our k-BDH will lead to generalizations of many such schemes. To illustrate the usefulness of our k-BDH family, we construct a family of selectively secure Identity-Based Encryption (IBE) systems based on it. Our system can be viewed as a generalization of the Boneh-Boyen IBE, however, the construction and proof require new ideas to fit the family. We then extend our methods to produces hierarchical IBEs and CCA security; and give a fully secure variant. In addition, we discuss the opportunities and challenges of building new systems under our weaker assumption family.
    [Show full text]
  • Circuit-Extension Handshakes for Tor Achieving Forward Secrecy in a Quantum World
    Proceedings on Privacy Enhancing Technologies ; 2016 (4):219–236 John M. Schanck*, William Whyte, and Zhenfei Zhang Circuit-extension handshakes for Tor achieving forward secrecy in a quantum world Abstract: We propose a circuit extension handshake for 2. Anonymity: Some one-way authenticated key ex- Tor that is forward secure against adversaries who gain change protocols, such as ntor [13], guarantee that quantum computing capabilities after session negotia- the unauthenticated peer does not reveal their iden- tion. In doing so, we refine the notion of an authen- tity just by participating in the protocol. Such pro- ticated and confidential channel establishment (ACCE) tocols are deemed one-way anonymous. protocol and define pre-quantum, transitional, and post- 3. Forward Secrecy: A protocol provides forward quantum ACCE security. These new definitions reflect secrecy if the compromise of a party’s long-term the types of adversaries that a protocol might be de- key material does not affect the secrecy of session signed to resist. We prove that, with some small mod- keys negotiated prior to the compromise. Forward ifications, the currently deployed Tor circuit extension secrecy is typically achieved by mixing long-term handshake, ntor, provides pre-quantum ACCE security. key material with ephemeral keys that are discarded We then prove that our new protocol, when instantiated as soon as the session has been established. with a post-quantum key encapsulation mechanism, Forward secret protocols are a particularly effective tool achieves the stronger notion of transitional ACCE se- for resisting mass surveillance as they resist a broad curity. Finally, we instantiate our protocol with NTRU- class of harvest-then-decrypt attacks.
    [Show full text]
  • Intro to Cryptography 1 Introduction 2 Secure Password Manager
    Programming Assignment 1 Winter 2021 CS 255: Intro to Cryptography Prof. Dan Boneh Due Monday, Feb. 8, 11:59pm 1 Introduction In many software systems today, the primary weakness often lies in the user’s password. This is especially apparent in light of recent security breaches that have highlighted some of the weak passwords people commonly use (e.g., 123456 or password). It is very important, then, that users choose strong passwords (or “passphrases”) to secure their accounts, but strong passwords can be long and unwieldy. Even more problematic, the user generally has many different services that use password authentication, and as a result, the user has to recall many different passwords. One way for users to address this problem is to use a password manager, such as LastPass and KeePass. Password managers make it very convenient for users to use a unique, strong password for each service that requires password authentication. However, given the sensitivity of the data contained in the password manager, it takes considerable care to store the information securely. In this assignment, you will be writing a secure and efficient password manager. In your implemen- tation, you will make use of various cryptographic primitives we have discussed in class—notably, authenticated encryption and collision-resistant hash functions. Because it is ill-advised to imple- ment your own primitives in cryptography, you should use an established library: in this case, the Stanford Javascript Crypto Library (SJCL). We will provide starter code that contains a basic tem- plate, which you will be able to fill in to satisfy the functionality and security properties described below.
    [Show full text]
  • User Authentication and Cryptographic Primitives
    User Authentication and Cryptographic Primitives Brad Karp UCL Computer Science CS GZ03 / M030 16th November 2016 Outline • Authenticating users – Local users: hashed passwords – Remote users: s/key – Unexpected covert channel: the Tenex password- guessing attack • Symmetric-key-cryptography • Public-key cryptography usage model • RSA algorithm for public-key cryptography – Number theory background – Algorithm definition 2 Dictionary Attack on Hashed Password Databases • Suppose hacker obtains copy of password file (until recently, world-readable on UNIX) • Compute H(x) for 50K common words • String compare resulting hashed words against passwords in file • Learn all users’ passwords that are common English words after only 50K computations of H(x)! • Same hashed dictionary works on all password files in world! 3 Salted Password Hashes • Generate a random string of bytes, r • For user password x, store [H(r,x), r] in password file • Result: same password produces different result on every machine – So must see password file before can hash dictionary – …and single hashed dictionary won’t work for multiple hosts • Modern UNIX: password hashes salted; hashed password database readable only by root 4 Salted Password Hashes • Generate a random string of bytes, r Dictionary• For user password attack still x, store possible [H(r,x after), r] in attacker seespassword password file file! Users• Result: should same pick password passwords produces that different aren’t result close to ondictionary every machine words. – So must see password file
    [Show full text]
  • To Change Your Ud Password(S)
    TO CHANGE YOUR UD PASSWORD(S) The MyCampus portal allows the user a single-signon for campus applications. IMPORTANT NOTICE AT BOTTOM OF THESE INSTRUCTIONS !! INITIAL PROCEDURE TO ALLOW YOU TO CHANGE YOUR PASSWORD ON THE UD NETWORK : 1. In your web browser, enter http://mycampus.dbq.edu . If you are logging in for the first time, you will be directed to answer (3) security questions. Also, be sure to answer one of the recovery methods. 2. Once the questions are answered, you will click on SUBMIT and then CONTINUE and then YES. 3. In one location, you will now find MyUD, Campus Portal, Email and UDOnline (Moodle). 4. You can now click on any of these apps and you will be logged in already. The email link will prompt you for the password a second time until we get all accounts set up properly. YOU MUST BE SURE TO LOGOUT OF EACH APPLICATION AFTER YOU’RE DONE USING IT !! TO CHANGE YOUR PASSWORD: 1. After you have logged into the MyCampus.dbq.edu website, you will see your username in the upper- right corner of the screen. 2. Click on your name and then go into My Account. 3. At the bottom, you will click on Change Password and then proceed as directed. 4. You can now logout. You will need to use your new password on your next login. Password must be a minimum of 6 characters and contain 3 of the following 4 categories: - Uppercase character - Lowercase character - Number - Special character You cannot use the previous password You’ll be required to change your password every 180 days.
    [Show full text]
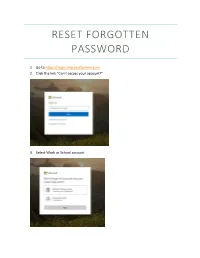
  • Reset Forgotten Password with Office365
    RESET FORGOTTEN PASSWORD 1. Go to https://login.microsoftonline.com 2. Click the link “Can’t access your account?” 3. Select Work or School account 4. Enter in your User ID with the @uamont.edu at the end and then enter the characters as seen in the picture. You can click the refresh button for a different set of letters. 5. You will have 3 options to verify your account and reset your password. This information was set up when you registered with self-service password reset. If you have not registered, please go to https://aka.ms/ssprsetup and enter in your information. A step by step guide on how to do this can be found here. a. Text your mobile phone b. Call your mobile phone c. Answer Security Questions 6. Choose one option and enter the information requested 7. Click Text for text my mobile phone, Call for call my mobile phone, or click Next when you’ve answered all security questions. a. If you have selected Text my mobile phone you will be required to enter in a verification code and click Next b. If you have select Call my mobile phone you will receive a call and will need to enter # to verify. 8. Enter in your new password and click Finish a. Note: If you receive the message, “Unfortunately, your password contains a word, phrase, or pattern that makes it easily guessable. Please try again with a different password.” Please try to create a password that does not use any dictionary words. b. Passwords must meet 3 of the 4 following requirements i.
    [Show full text]
  • Implementation and Performance Evaluation of XTR Over Wireless Network
    Implementation and Performance Evaluation of XTR over Wireless Network By Basem Shihada [email protected] Dept. of Computer Science 200 University Avenue West Waterloo, Ontario, Canada (519) 888-4567 ext. 6238 CS 887 Final Project 19th of April 2002 Implementation and Performance Evaluation of XTR over Wireless Network 1. Abstract Wireless systems require reliable data transmission, large bandwidth and maximum data security. Most current implementations of wireless security algorithms perform lots of operations on the wireless device. This result in a large number of computation overhead, thus reducing the device performance. Furthermore, many current implementations do not provide a fast level of security measures such as client authentication, authorization, data validation and data encryption. XTR is an abbreviation of Efficient and Compact Subgroup Trace Representation (ECSTR). Developed by Arjen Lenstra & Eric Verheul and considered a new public key cryptographic security system that merges high level of security GF(p6) with less number of computation GF(p2). The claim here is that XTR has less communication requirements, and significant computation advantages, which indicate that XTR is suitable for the small computing devices such as, wireless devices, wireless internet, and general wireless applications. The hoping result is a more flexible and powerful secure wireless network that can be easily used for application deployment. This project presents an implementation and performance evaluation to XTR public key cryptographic system over wireless network. The goal of this project is to develop an efficient and portable secure wireless network, which perform a variety of wireless applications in a secure manner. The project literately surveys XTR mathematical and theoretical background as well as system implementation and deployment over wireless network.
    [Show full text]
  • Optimizing a Password Hashing Function with Hardware-Accelerated Symmetric Encryption
    S S symmetry Article Optimizing a Password Hashing Function with Hardware-Accelerated Symmetric Encryption Rafael Álvarez 1,* , Alicia Andrade 2 and Antonio Zamora 3 1 Departamento de Ciencia de la Computación e Inteligencia Artificial (DCCIA), Universidad de Alicante, 03690 Alicante, Spain 2 Fac. Ingeniería, Ciencias Físicas y Matemática, Universidad Central, Quito 170129, Ecuador; [email protected] 3 Departamento de Ciencia de la Computación e Inteligencia Artificial (DCCIA), Universidad de Alicante, 03690 Alicante, Spain; [email protected] * Correspondence: [email protected] Received: 2 November 2018; Accepted: 22 November 2018; Published: 3 December 2018 Abstract: Password-based key derivation functions (PBKDFs) are commonly used to transform user passwords into keys for symmetric encryption, as well as for user authentication, password hashing, and preventing attacks based on custom hardware. We propose two optimized alternatives that enhance the performance of a previously published PBKDF. This design is based on (1) employing a symmetric cipher, the Advanced Encryption Standard (AES), as a pseudo-random generator and (2) taking advantage of the support for the hardware acceleration for AES that is available on many common platforms in order to mitigate common attacks to password-based user authentication systems. We also analyze their security characteristics, establishing that they are equivalent to the security of the core primitive (AES), and we compare their performance with well-known PBKDF algorithms, such as Scrypt and Argon2, with favorable results. Keywords: symmetric; encryption; password; hash; cryptography; PBKDF 1. Introduction Key derivation functions are employed to obtain one or more keys from a master secret. This is especially useful in the case of user passwords, which can be of arbitrary length and are unsuitable to be used directly as fixed-size cipher keys, so, there must be a process for converting passwords into secret keys.
    [Show full text]
  • Strong Password-Based Authentication in TLS Using the Three-Party Group Diffie–Hellman Protocol
    284 Int. J. Security and Networks, Vol. 2, Nos. 3/4, 2007 Strong password-based authentication in TLS using the three-party group Diffie–Hellman protocol Michel Abdalla* École normale supérieure – CNRS, LIENS, Paris, France E-mail: [email protected] *Corresponding author Emmanuel Bresson Department of Cryptology, CELAR Technology Center, Bruz, France E-mail: [email protected] Olivier Chevassut Lawrence Berkeley National Laboratory, Berkeley, CA, USA E-mail: [email protected] Bodo Möller Horst Görtz Institute for IT Security, Ruhr-Universität Bochum, Bochum, Germany E-mail: [email protected] David Pointcheval École normale supérieure – CNRS, LIENS, Paris, France E-mail: [email protected] Abstract: The internet has evolved into a very hostile ecosystem where ‘phishing’ attacks are common practice. This paper shows that the three-party group Diffie-Hellman key exchange can help protect against these attacks. We have developed password-based ciphersuites for the Transport Layer Security (TLS) protocol that are not only provably secure but also believed to be free from patent and licensing restrictions based on an analysis of relevant patents in the area. Keywords: password authentication; group Diffie–Hellman key exchange; transport layer security; TLS. Reference to this paper should be made as follows: Abdalla, M., Bresson, E., Chevassut, O., Möller, B. and Pointcheval, D. (2007) ‘Strong password-based authentication in TLS using the three-party group Diffie-Hellman protocol’, Int. J. Security and Networks, Vol. 2, Nos. 3/4, pp.284–296. Biographical notes: Michel Abdalla is currently a Researcher with the Centre National de la Recherche Scientifique (CNRS), France and a Member of the Cryptography Team at the Ecole Normale Supérieure (ENS), France.
    [Show full text]
  • DRAFT Special Publication 800-56A, Recommendation for Pair-Wise Key
    The attached DRAFT document (provided here for historical purposes) has been superseded by the following publication: Publication Number: NIST Special Publication (SP) 800-56A Revision 2 Title: Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography Publication Date: 05/13/2013 • Final Publication: https://doi.org/10.6028/NIST.SP.800-56Ar2 (which links to http://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-56Ar2.pdf). • Information on other NIST Computer Security Division publications and programs can be found at: http://csrc.nist.gov/ The following information was posted with the attached DRAFT document: Aug 20, 2012 SP 800-56 A Rev.1 DRAFT Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography (Draft Revision) NIST announces the release of draft revision of Special Publication 800-56A, Recommendation for Pair-Wise Key Establishment Schemes Using Discrete Logarithm Cryptography. SP 800-56A specifies key-establishment schemes based on the discrete logarithm problem over finite fields and elliptic curves, including several variations of Diffie-Hellman and MQV key establishment schemes. The revision is made on the March 2007 version. The main changes are listed in Appendix D. Please submit comments to 56A2012rev-comments @ nist.gov with "Comments on SP 800-56A (Revision)" in the subject line. The comment period closes on October 31, 2012. NIST Special Publication 800-56A Recommendation for Pair-Wise August 2012 Key-Establishment Schemes Using Discrete Logarithm Cryptography (Draft Revision) Elaine Barker, Lily Chen, Miles Smid and Allen Roginsky C O M P U T E R S E C U R I T Y Abstract This Recommendation specifies key-establishment schemes based on the discrete logarithm problem over finite fields and elliptic curves, including several variations of Diffie-Hellman and MQV key establishment schemes.
    [Show full text]
  • Password Cracking
    Password Cracking Sam Martin and Mark Tokutomi 1 Introduction Passwords are a system designed to provide authentication. There are many different ways to authenticate users of a system: a user can present a physical object like a key card, prove identity using a personal characteristic like a fingerprint, or use something that only the user knows. In contrast to the other approaches listed, a primary benefit of using authentication through a pass- word is that in the event that your password becomes compromised it can be easily changed. This paper will discuss what password cracking is, techniques for password cracking when an attacker has the ability to attempt to log in to the system using a user name and password pair, techniques for when an attacker has access to however passwords are stored on the system, attacks involve observing password entry in some way and finally how graphical passwords and graphical password cracks work. Figure 1: The flow of password attacking possibilities. Figure 1 shows some scenarios attempts at password cracking can occur. The attacker can gain access to a machine through physical or remote access. The user could attempt to try each possible password or likely password (a form of dictionary attack). If the attack can gain access to hashes of the passwords it is possible to use software like OphCrack which utilizes Rainbow Tables to crack passwords[1]. A spammer may use dictionary attacks to gain access to bank accounts or other 1 web services as well. Wireless protocols are vulnerable to some password cracking techniques when packet sniffers are able to gain initialization packets.
    [Show full text]
  • 21. the Diffie-Hellman Problem
    Chapter 21 The Diffie-Hellman Problem This is a chapter from version 2.0 of the book “Mathematics of Public Key Cryptography” by Steven Galbraith, available from http://www.math.auckland.ac.nz/˜sgal018/crypto- book/crypto-book.html The copyright for this chapter is held by Steven Galbraith. This book was published by Cambridge University Press in early 2012. This is the extended and corrected version. Some of the Theorem/Lemma/Exercise numbers may be different in the published version. Please send an email to [email protected] if youfind any mistakes. This chapter gives a thorough discussion of the computational Diffie-Hellman problem (CDH) and related computational problems. We give a number of reductions between computational problems, most significantly reductions from DLP to CDH. We explain self-correction of CDH oracles, study the static Diffie-Hellman problem, and study hard bits of the DLP and CDH. We always use multiplicative notation for groups in this chapter (except for in the Maurer reduction where some operations are specific to elliptic curves). 21.1 Variants of the Diffie-Hellman Problem We present some computational problems related to CDH, and prove reductions among them. The main result is to prove that CDH and Fixed-CDH are equivalent. Most of the results in this section apply to both algebraic groups (AG) and algebraic group quotients (AGQ) of prime orderr (some exceptions are Lemma 21.1.9, Lemma 21.1.16 and, later, Lemma 21.3.1). For the algebraic group quotientsG considered in this book then one can obtain all the results by lifting from the quotient to the covering groupG ′ and applying the results there.
    [Show full text]