The Pennsylvania State University the Graduate School
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1St IEEE 5G World Forum
1st IEEE 5G World Forum Roadmap Applications & Services Workgroup: 5G is Power Starved Brian Zahnstecher, Principal, IEEE Senior Member Chair, SF Bay IEEE Power Electronics Society (PELS) Power Content Owner, IEEE 5G Initiative Roadmap, Application Services Workgroup Co-chair, IEEE 5G Initiative Webinar Chair, IEEE 5G Energy Efficiency Tutorial [email protected] +1 (508) 847-5747 PowerRox™ www.powerrox.com Twitter: @PowerRoxLLC LinkedIn: www.linkedin.com/in/zahnstecher Monday, July 9, 2018 DISCLAIMER There is neither any sponsored promotion nor bias toward any of the products/organizations mentioned in this tutorial. Any vendor-specific content is provided for example purposes only. 2 ALL INFORMATION SHALL BE CONSIDERED SPEAKER PROPERTY UNLESS OTHERWISE SUPERSEDED BY ANOTHER DOCUMENT. OVERVIEW • Marketing Projections Vs. Reality • What is the power gap? • Power Sources Vs. Loads • Making the Projections a Reality • Summary / Conclusions 3 ALL INFORMATION SHALL BE CONSIDERED SPEAKER PROPERTY UNLESS OTHERWISE SUPERSEDED BY ANOTHER DOCUMENT. Market Projections Vs. Reality • Network Usage Projections . How do these translate to load projections? . Which components ARE Moore’s Law Like? o Which are NOT? 54% YoY growth!!! IMAGES CREDIT: "Ericsson Mobility Report 2018," Ericsson, June 2018. 4 ALL INFORMATION SHALL BE CONSIDERED SPEAKER PROPERTY UNLESS OTHERWISE SUPERSEDED BY ANOTHER DOCUMENT. Market Projections Vs. Reality • Network Usage Projections . How will shifts in global usage markets impact the availability of power? . Is WW power projected to grow on the same trajectory? IMAGES CREDIT: "Estimated U.S. Energy Net Generation 1950-2018," US EIA, July 2018. IMAGES CREDIT: "Ericsson Mobility Report 2018," Ericsson, June 2018. 5 ALL INFORMATION SHALL BE CONSIDERED SPEAKER PROPERTY UNLESS OTHERWISE SUPERSEDED BY ANOTHER DOCUMENT. -

International Journal of Recent Technology and Engineering (IJRTE) ISSN: 2277-3878, Volume-8 Issue-5, January 2020
International Journal of Recent Technology and Engineering (IJRTE) ISSN: 2277-3878, Volume-8 Issue-5, January 2020 5G Massive Multiple Input and Multiple Output System with Maximum Spectral Performance N C A Boovarahan, K. Umapathy channel fading function isn't always clearly exploited. Abstract: Massive MIMO is the presently maximum compelling Various subcarrier [15-18]choice techniques are sub-6 GHz physical-layer era for destiny wireless access. Excellent mentioned by manner of dividing the spectrum allocation spectral overall performance finished through manner of spatial techniques in broad classes i.e. Single channel allocation and multiplexing of many terminals inside the equal time-frequency resource. The 5G structures are characterized through excessive group of channel allocation. The SCS-MC-CDMA device transmission records prices, 1Gbps and above, so large bandwidth allocates to every person and selected a wide form of transmission is expected. The most vital objectives within the 5G sub-vendors [16]. wireless systems design is to deal with the excessive inter photograph interference (ISI) as a consequence of the high II. SUB CHANNEL SELECTION ALGORITHM & statistics fees, and using the accessible spectral bandwidth in MAXIMUM THROUGHPUT resourceful way.MC-CDMA is categorized in to two methods that is ODFM and CDMA. Efficient useful resource allocation is the The main end result of our paper shows that the Eigen principle trouble within the development of fourth generation values of the correlation matrix of the effective channel can be cellular communication systems. For utilizing the internet and properly approximated via sampling values of the multimedia a maximum data fee is preferred, so in this paper the general performance of MC-CDMA systems the usage of Sylow autocorrelation of the time-varying transfer function. -

First Year First Semester
First year First Semester. ET/Hum/T/A/111 HUMANITIES-A 4 Pds/Wk Credit 4 English - 2 Pds/week - 50 Marks Sociology - 2 Pds/week - 50 Marks HUMANITIES 1. Basic writing skills 2. Report, Covering Letter & Curriculum-Vitae writing 3. Reading and Comprehension 4. Selected Short Stories Text Book: ENGLISH FOR ALL SOCIOLOGY 1. Sociology: nature and scope of sociology - sociology and other social sciences - sociological perspectives and explanation of social issues 2. Society and technology: impact of technology on the society - a case study 3. Social stratification: systems of social stratification - determinants of social stratification - functionalist, conflict and elitist perspectives on social stratification 4. Work: meaning and experience of work: postindustrial society- post-fordism and the flexible firm 5. Development - conceptions of and approaches to development - the roles of state and the market in the development 6. Globalization: the concept of globalization - globalization and the nation state - development and globalization in post colonial times. 7. Industrial policy and technological change in india - the nature and role of the state in India 8. Technology transfer: the concept and types of technology transfer-dynamics of technology transfer 9. Technology assessment: the concept - steps involved in technology assessment 10. Environment: sociological perspectives on environment - environmental tradition and values in ancient india 11. The development of management: scientific management - organic organization - net work organization - post modern organization - debureaucratization - transformation of management 12. Technological problems and the modern society: selected case studies – electric power crisis, industrial and/or environmental disaster, or nuclear accident ET/T/112 PHYSICAL ELECTRONICS 3 Pds/Wk Credit 3 Crystal structure: periodic arrays of atoms, fundamental type of lattices, crystal direction & planes. -

Mc/Ds-Cdma Versus Sc/Ds-Cdma in Mobile Radio: Spectral Efficiency Approach
WSEAS TRANSACTIONS on COMMUNICATIONS P. Varzakas MC/DS-CDMA VERSUS SC/DS-CDMA IN MOBILE RADIO: SPECTRAL EFFICIENCY APPROACH P.Varzakas Department of Electronics Technological Educational Institute of Lamia 3o Km Old Road Lamia-Athens, GR 35100, Lamia e-mail: [email protected] Abstract—The spectral efficiency of a multicarrier direct-sequence code-division multiple-access (MC/DS-CDMA) cellular system operating in a mobile radio environment with Rayleigh fading, is investigated. In this work, spectral efficiency is evaluated in terms of channel capacity (in the Shannon sense) per user, estimated in an average sense. It is analytically shown that, under normalized condi- tions and assuming a static model of operation, MC/DS-CDMA spectral efficiency, on downlink, is higher than that of single-carrier direct-sequence code-division multiple-access (SC/DS-CDMA). This result is justified by the combination of path-diversity reception, achieved by a conventional coherent maximal-ratio combining (MRC) RAKE receiver, and physical frequency diversity potential provided, in a fading environment, by frequency-division multiplexing on a set of orthogonal carriers. It is shown that the increase of the carrier frequencies, in the MC/DS-CDMA cellular system, leads to a respective improvement of the spectral efficiency achieved. Key-Words:-Spectral efficiency, multicarrier modulation, code-division multiple access, cellular sys- tems. 1 Introduction can also be estimated in an average sense while its degradation is anticipated to a certain degree by uti- In the literature, there has been a growing inter- lizing some kind of diversity reception technique, est in broadband transmission over time-variant [3, 4]. -
School of Engineering & Technology B. Tech Electronics And
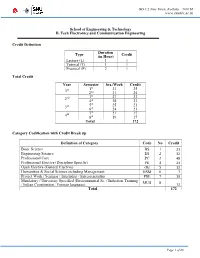
DG 1/2 New Town, Kolkata – 700156 www.snuniv.ac.in School of Engineering & Technology B. Tech Electronics and Communication Engineering Credit Definition Duration Type (in Hour) Credit Lecture (L) 1 1 Tutorial (T) 1 1 Practical (P) 2 1 Total Credit Year Semester hrs./Week Credit 1st 31 25 1st 2nd 31 25 3rd 27 23 2nd 4th 28 23 5th 25 21 3rd 6th 24 21 7th 21 17 4th 8th 19 17 Total 172 Category Codification with Credit Break up Definition of Category Code No Credit Basic Science BS 1 21 Engineering Science ES 2 32 Professional Core PC 3 48 Professional Elective (Discipline Specific) PE 4 21 Open Elective (General Elective) OE 5 12 Humanities & Social Science including Management HSM 6 7 Project Work / Seminar / Internship / Entrepreneurship PSE 7 19 Mandatory / University Specified (Environmental Sc. / Induction Training MUS 8 / Indian Constitution / Foreign language) 12 Total 172 Page 1 of 66 DG 1/2 New Town, Kolkata – 700156 www.snuniv.ac.in School of Engineering & Technology B. Tech Electronics and Communication Engineering Category wise Credit Distribution Subject Codification 1 X X X X X X 11 If “Type” = 3, then 1 – Seminar, 2 Course No – project, 3 – Internship/Entrepreneurship, 4 - Type Department Semester (1..8) Viva Code 1 – L/L+T, 2 – L+P, 3 – Sessional, 4 – P/Workshop Category Degree 1 – BS, 2 – ES, 3 – PC, 4 – PE, 5 – OE, 6 – HSM, 7 – PSE, 8 – MUS 1 – B.Tech 2 – M.Tech 3 – PhD Page 2 of 66 DG 1/2 New Town, Kolkata – 700156 www.snuniv.ac.in School of Engineering & Technology B. -

Dongning Guo Curriculum Vitae
Dongning Guo Curriculum Vitae Contact Department of Electrical & Computer Engineering Northwestern University 2145 Sheridan Rd., Evanston, IL 60208 Tel: +1-847-491-3056 Fax: +1-847-491-4455 Email: [email protected] http://users.ece.northwestern.edu/∼dguo Research Interests Blockchain technologies, wireless communications, information theory, com- munication networks, and machine learning. Employment 9/2020–present Professor (by courtesy) Department of Computer Science Northwestern University, Evanston, IL, USA. 9/2015–present Professor Department of Electrical & Computer Engineering Northwestern University, Evanston, IL, USA. 9/2010–8/2015 Associate Professor Department of Electrical Engineering & Computer Science Northwestern University, Evanston, IL, USA. 9/2004–8/2010 Assistant Professor Department of Electrical Engineering & Computer Science Northwestern University, Evanston, IL, USA. 7/2014–6/2015 Visiting Scientist (courtesy appointment) Research Laboratory of Electronics Massachusetts Institute of Technology, Cambridge, MA, USA. 3/2011–8/2011 Consultant New Jersey Research & Development Center, Qualcomm Inc., Bridgewater, NJ, USA. 10/2010–2/2011 Visiting Professor Institute of Network Coding Chinese University of Hong Kong, China. 8/2006–9/2006 Visiting Professor 1 Department of Electronics & Telecommunications Norwegian University of Science & Technology, Trondheim, Norway. 2/1998–8/1999 Research & Development Engineer Centre for Wireless Communications (now the Institute for Infocomm Re- search), Singapore. Education Ph.D., Electrical Engineering, 2004 Princeton University, Princeton, NJ. Thesis: Gaussian Channels: Information, Estimation and Multiuser Detection Adviser: Sergio Verdu´ Committee: Sergio Verdu,´ Shlomo Shamai, H. Vincent Poor, Robert Calder- bank, Mung Chiang. M.A., Electrical Engineering, 2001 Princeton University, Princeton, NJ. M.Eng., Electrical Engineering, 1999 National University of Singapore, Singapore. Thesis: Linear Parallel Interference Cancellation in CDMA Adviser: Lars K. -

PG-Curriculum (Structure and Course Contents) Electronics Engineering with Effect from July 2018
PG-Curriculum (Structure and Course Contents) Electronics Engineering With effect from July 2018 Electronics and Communication Engineering Punjab Engineering College (Deemed to be University) Chandigarh PG Curriculum Structure Segment {Fractal system Sr. (each section of 0.5 Course Stream Course Name Credits No. Credits and 7 contact hours)} 1 2 3 4 5 6 Semester I Internet of Things 1.5 1. Soft Computing Machine Learning 1.5 Design of experiments and Design of experiments and research 2. 3 research methodology methodology 3. Program Core-I Advanced Communication Systems 3 4. Program Core-II Telecommunication Systems 3 Advanced Digital Signal Processing Program Microwave Integrated Circuit 1.5 Elective-I: E1 RF and Microwave MEMS-I FPGA and ASIC 5. Semiconductor Microwave Devices Program Digital Image Processing 1.5 Elective-II: E2 RF and Microwave MEMS-II FPGA Based System Design Engineering EM1: Fourier Transforms 1 6. Mathematics EM2: Numerical Methods 1 (EM) EM3: Optimization Techniques-II 1 Total Credits 18 1 Segment {Fractal system Sr. (each section of 0.5 Course Stream Course Name Credits No. Credits and 7 contact hours)} 1 2 3 4 5 6 Semester II Communication Skills (CS) 1.5 Soft Skills and 1. Management and Entrepreneurship(M)/IPR 1 Management Professional Ethics (PE) 0.5 Program Core 2. Optoelectronics 3 III Program Core- 3. Wireless Sensors Networks 3 IV Microcontroller Based Systems Semiconductor Device Modelling Program Thin Film Deposition and Device 1.5 Elective-III: E3 Fabrication-I Analog VLSI Circuit Design Coding Theory and Application 4. Digital VLSI Circuit Design Nano Electronic Devices Program Thin Film Deposition and Device 1.5 Elective-IV: E4 Fabrication-II Embedded Systems Open Elective 1 1.5 Neural Networks 5. -

Spectral Efficiency Comparison of Ofdm and Mc-Cdma with Carrier Frequency Offset
RADIOENGINEERING, VOL. 26, NO. 1, APRIL 2017 221 Spectral Efficiency Comparison of OFDM and MC-CDMA with Carrier Frequency Offset Junaid AHMED Dept. of Electrical Engineering, COMSATS Institute of Information Technology, Tarlai Kalan, 45550 Islamabad, Pakistan [email protected] Submitted March 4, 2016 / Accepted December 15, 2016 Abstract. Inter-carrier interference and multiple access ficiency degradation of MC-CDMA, in the presence of CFO, interference due to carrier frequency offset (CFO) are two over a frequency selective Rayleigh fading environment is major factors that deteriorate the performance of orthogonal studied in [10], [11]; a lower bound of spectral efficiency in frequency division multiple access (OFDMA) and multicar- the presence of asynchronous interferers is derived. Previous rier code division multiple access (MC-CDMA) in wireless research work on the performance of OFDMA in the presence communication. This paper presents a new mathematical of CFO has mostly focused on symbol/bit error rate [12–16]. analysis for spectral efficiency of OFDMA communication The analyses mostly use Gaussian or improved Gaussian ap- systems over a frequency selective Rayleigh fading environ- proximation, which are not accurate due to correlation in ment in the presence of multiple users. It also compares the frequency response of the adjacent subchannels, especially spectral efficiency performance of OFDMA and MC-CDMA at low bit error rates [17]. In [18–20], average capacity/ spec- at different load, signal-to-noise ratio, CFO and delay spread tral efficiency of OFDM with CFO in Rician and Rayleigh conditions. MC-CDMA is found to be more resilient to CFO fading environment is analyzed respectively. -

Optimizing Spectral Efficiency in Multiwavelength Optical CDMA System Tung-Wah Frederick Chang, Student Member, IEEE, and Edward H
1442 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 51, NO. 9, SEPTEMBER 2003 Optimizing Spectral Efficiency in Multiwavelength Optical CDMA System Tung-Wah Frederick Chang, Student Member, IEEE, and Edward H. Sargent, Member, IEEE Abstract—Prime codes are excellent candidates for use in multiwavelength optical code-division multiple-access (O-CDMA) systems. We show that in an O-CDMA system using two-dimen- sional single-pulse-per-row codes, a single choice of the number of wavelength channels can accommodate different numbers of users with maximal spectral efficiency. The optimum single-user-detec- tion spectral efficiency of the system can be reached using AND detection. A fixed-hardware network can readily be adapted in response to changes in the number of users and traffic load. Index Terms—Adaptive networks, optical code-division multiple access (O-CDMA), spectral efficiency, two-dimensional (2-D) codes. Fig. 1. An example of SPR prime code from [9]. In this case, x a S, v a S, and aPS. is a time duration of a chip. I. INTRODUCTION PTICAL code-division multiple access (O-CDMA) has In this letter, we explore the effect of distribution of band- attracted attention for over a decade [1]–[3]. While the O width between the temporal and wavelength/spatial domains on vast bandwidth of the optical fiber medium provides high-speed the spectral efficiency of the system. Next, we investigate the point-to-point data transmission, the CDMA scheme facilitates effect of detection method on the achieved spectral efficiency random access to the channel in a bursty traffic environment. of the system. -
Télécom Paris (ENST) Institut Eurécom THESE Souad Guemghar
T´el´ecom Paris (ENST) Institut Eur´ecom THESE Pr´esent´ee pour Obtenir le Grade de Docteur de l'Ecole Nationale Sup´erieure des T´el´ecommunications Sp´ecialit´e: Communication et Electronique Souad Guemghar Techniques de Codage Avanc´ees et Applications au CDMA Pr´esident P. Sol´e, I3S (Sophia Antipolis, France) Rapporteurs E. Biglieri, Politecnico de Torino (Turin, Italie) J. Boutros, ENST (Paris, France) Examinateurs A. Glavieux, ENST Bretagne (Brest, France) A. Roumy, IRISA (Rennes, France) Directeur de th`ese G. Caire, Institut Eur´ecom (Sophia Antipolis, France) 29 Janvier 2004 T´el´ecom Paris (ENST) Institut Eur´ecom THESIS In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy from Ecole Nationale Sup´erieure des T´el´ecommunications Specializing: Communication and Electronics Souad Guemghar Advanced Coding Techniques and Applications to CDMA President P. Sol´e, I3S (Sophia Antipolis, France) Readers E. Biglieri, Politecnico de Torino (Torino, Italy) J. Boutros, ENST (Paris, France) Examiners A. Glavieux, ENST Bretagne (Brest, France) A. Roumy, IRISA (Rennes, France) Thesis supervisor G. Caire, Institut Eur´ecom (Sophia Antipolis, France) January 29th 2004 A mes parents, ma soeur et mon mari Remerciements Mon travail de th`ese est maintenant presque arriv´e a` sa fin et c'est le moment d'exprimer ma gratitude et mes remerciements envers certaines personnes. Tout d'abord, je remercie mon directeur de th`ese Giuseppe Caire de m'avoir donn´e l'occasion de faire cette th`ese qui constitue une exp´erience extr^emement enrichissante sur plusieurs plans. Il a souvent eu de brillantes id´ees de recherche, ce qui m'a fait explorer plusieurs domaines diff´erents. -

Walchand College of Engineering, Sangli (Government Aided Autonomous Institute)
Walchand College of Engineering, Sangli (Government Aided Autonomous Institute) Course Contents (Syllabus) for Third Year B. Tech. (Electronics Engineering) Sem – V to VI AY 2020-21 Professional Core (Theory) Title of the Course: 4EN 301 Digital Signal Processing L T P Cr 3 0 0 3 Pre-Requisite Courses: Signals and Systems Textbooks: 1. “Digital Signal Processing: A Computer Based Approach”, Sanjit K. Mitra, 4th Edition, Tata McGraw-Hill Publication. 2. “Discrete Time Signal Processing”, Oppenheim & Schafer,2nd Edition, Pearson education. References: 1. “Digital Signal Processing”, J. G. Proakis, Prentice Hall India Course Objectives : 1. To illustrate the fundamental concepts of Signal Processing. 2. To explain the different techniques for design of filters and multirate systems. 3. To enable the students for the design and development of DSP systems. Course Learning Outcomes: CO After the completion of the course the student should be able Bloom’s Cognitive to level Descriptor CO1 Solve Discrete Fourier Transform in efficient manner III Apply CO2 Analyze the structures for Discrete Time systems IV Classify CO3 Design the FIR, IIR Digital Filters for given specifications. VI Create CO4 Describe the fundamentals of Multirate DSP and Wavelet II Explain Transform CO-PO Mapping : 1 2 3 4 5 6 7 8 9 10 11 12 PSO1 PSO2 CO1 3 2 CO2 3 2 CO3 2 2 CO4 2 2 Assessments : Teacher Assessment: Two components of In Semester Evaluation (ISE), One Mid Semester Examination (MSE) and one End Semester Examination (ESE) having 20%, 30% and 50% weights respectively. Assessment Marks ISE 1 10 MSE 30 ISE 2 10 ESE 50 ISE 1 and ISE 2 are based on assignment/declared test/quiz/seminar etc. -

Spectral Efficiency of MIMO Multiaccess Systems with Single-User Decoding Ashok Mantravadi, Student Member, IEEE, Venugopal V
382 IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 21, NO. 3, APRIL 2003 Spectral Efficiency of MIMO Multiaccess Systems With Single-User Decoding Ashok Mantravadi, Student Member, IEEE, Venugopal V. Veeravalli, Senior Member, IEEE, and Harish Viswanathan, Member, IEEE Abstract—The use of multiple antennas at the transmitter and mobile may be practical. In this paper, we study potential gains the receiver is considered for the uplink of cellular communica- from using multiple antennas for uplink cellular systems, with tion systems. The achievable spectral efficiency in bits/s/Hz is used a focus on wideband code-division multiple-access (CDMA) as the criterion for comparing various design choices. The focus is on wideband code-division multiple-access (CDMA) systems when systems. the receiver uses the matched-filter or the minimum mean-squared In studying such multiantenna systems over fading chan- error detector, followed by single-user decoders. The spreading se- nels, an important aspect is the availability of channel state quences of the CDMA system are assumed to be random across information (CSI) at both ends of the link. We assume perfect the users, but could be dependent across the transmit antennas of each user. Using analytical results in the large system asymptote, channel state information at the receiver (base station). While guidelines are provided for the sequence design across the transmit availability of CSI at the transmitter allows for better perfor- antennas and for choosing the number of antennas. In addition, mance, the mobile is limited by allowable complexity as well as comparisons are made between (random) CDMA and orthogonal availability of channel feedback.