Dynamics of Isolated Magnetic Bright Points Derived from Hinode/SOT G-Band Observations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Hinode Project and Science Center (Hinode-SC)
Hinode Project and Science Center (Hinode-SC) Shinsuke Imada (Nagoya Univ., ISEE) Characteristics of the Advanced Telescopes | Hinode Science Center at NAOJ 2019/10/13 22(30 For Researchers 日本語 シェア Tweet “Hinode” Unveils To do research Information Gallery For Researchers the Mysteries of the Sun using Hinode data TOP "Hinode" Unveils the Mysteries of the Sun Characteristics of the Advanced Telescopes Solar Observing Satellite "Hinode" (SOLAR-B) | Hinode Science Center at NAOJ 2019/10/13 22(29 "Hinode" Unveils Characteristics of the Advanced Telescopes the Mysteries of the For Researchers 日本語 Sun Tweet シェア Overview of “Hinode” “Hinode” Unveils To do research Characteristics of the Advanced Telescopes Solar Observing Information Gallery For Researchers Satellite "Hinode" the Mysteries of the Sun using Hinode data (SOLAR-B) The Sun's atmosphere is comprised of layers. The layers beneath the surface (photosphere) cannot be TOP "Hinode" UnveilsSolar the Mysteries of the Sun ObservingSolar Observing Satellite "Hinode" (SOLAR-B) Satelliteseen “ directly,Hinode but the upper layers ”above (SOLAR the photosphere each emit- differentB) wavelengths of lights. So, About the "Hinode" Project you can see each layer by changing the observing wavelength. By loading three telescopes observing in "Hinode" Unveils Solar Observing Satellite "Hinode" (SOLAR-B) different wavelengththe Mysteries ranges, of the Hinode can simultaneously observe from the photosphere to the corona (upper atmosphere).Sun Characteristics of the Advanced Telescopes Overview of “Hinode” -

Co-Aligned IRIS, SDO and Hinode Data Cubes Release 1.0
Co-aligned IRIS, SDO and Hinode data cubes Release 1.0 Milan Gošic´ Feb 26, 2020 CONTENTS 1 Introduction 1 1.1 About this Guide.............................................1 1.2 Synopsis of the IRIS, Hinode and SDO missions............................1 1.3 Hinode and SDO data cubes co-aligned with IRIS observations....................2 2 Finding and downloading IRIS-SDO-Hinode co-aligned data cubes5 2.1 Using the IRIS Webpage (HCR).....................................5 2.2 Using SSWIDL..............................................5 3 Reading and browsing IRIS-SDO-Hinode co-aligned data cubes 11 3.1 Reading level 2 co-aligned SDO and Hinode datasets.......................... 11 3.2 Browsing co-aligned SDO and Hinode data cubes with CRISPEX................... 13 i ii CHAPTER ONE INTRODUCTION 1.1 About this Guide The purpose of this guide is to provide detailed instructions on how users can find, download, browse, and analyze co-aligned level 2 data obtained with The Interface Region Imaging Spectrograph (IRIS), the Atmospheric Imaging Assembly (AIA) on board the Solar Dynamics Observatory (SDO), and Hinode/SOT level 2 data. The IRIS team at the Lockheed Martin Solar and Astrophysics Laboratory (LMSAL) created new data cubes consisting of the Hinode/SOT and SDO/AIA images co-aligned with the simultaneous IRIS observations. These datasets all have the same IRIS level 2 FITS format, therefore can be accessed and examined using the IRIS SolarSoft software. In this guide, we provide step by step instructions how to access, read, and visualize these newly created co-aligned data cubes. In particular, we describe: • How to find data using SolarSoft IDL routines; • How to acquire data sets using either SolarSoft or Heliophysics Coverage Registry (HCR); • How to read data and visualize them using SolarSoft routines or Crisp Spectral Explorer (CRISPEX). -

Development of 60Μm Pitch Cdte Double-Sided Strip Detector for FOXSI-3 Rocket Experiment
Development of 60µm pitch CdTe double-sided strip detector for FOXSI-3 rocket experiment Kento Furukawa(U-Tokyo, ISAS/JAXA) Shin'nosuke Ishikawa, Tadayuki Takahashi, Shin Watanabe(ISAS/JAXA), Koichi Hagino(Tokyo University of Science), Shin'ichiro Takeda(OIST), P.S. Athiray, Lindsay Glesener, Sophie Musset, Juliana Vievering (U. of Minnesota), Juan Camilo Buitrago Casas , Säm Krucker (SSL/UCB), and Steven Christe (NASA/GSFC) 1 2 CdTe semiconductor and diode device Cadmium Telluride semiconductor : • High density • Large atomic number • High efficiency Issue : small µτ product especially for holes 260eV(FWHM) • Uniform & thin device @6.4keV 1400V,-40℃ • Schottky Diode (Takahashi et al. 1998 ) High bias voltage full charge collection + high energy resolution Takahashi et al. (2005) 3 Application of CdTe Diode Double-sided Strip Detector Watanabe et al. 2009 Anode(Pt): Ohmic contact Cathode(Al): Schottky contact Astrophysical Application • Hard X-ray Imager(HXI) onboard Hitomi(ASTRO-H) satellite • FOXSI rocket mission Medical Application • Small animal SPECT system (OIST/JAXA) 4 Hard X-ray study of the Sun Observation Target : the Sun Corona and flare Scientific Aim • Coronal Heating (thermal emission) • Particle Acceleration (non-thermal emission ) →Sensitive Hard X-ray imaging and spectral observation is the key especially for small scale flares study Soft X-ray image by Hinode (micro and nano) (NAOJ/JAXA) So far only Indirect Imaging e.g. RHESSI spacecraft (Rotational Modulation collimator) No direct imaging in hard X-ray band for solar mission 5 FOXSI rocket mission FOXSI experiment (UCB/SSL, NASA, UMN, ISAS/JAXA) Indirect Direct Imaging Spectroscopy with Focusing Optics in Hard X-ray Hard X-ray telescopes + CdTe focal plane detectors FOXSI’s hard X-ray telescope clearly identified a micro-flare with high S/N ratio Direct Telescope Angular resolution : 5 arcsec (FWHM) Focal plane detector 50µm on focal plane Krucker et al. -

Message from the Director General September 2017 Saku Tsuneta Director General
Message from the Director General September 2017 Saku Tsuneta Director General Institute of Space and Astronautical Science Japan Aerospace Exploration Agency On April 28, 2016, the Japan former ISAS project managers, and levels, the satellite was declared to Aerospace Exploration Agency an Action Plan for Reforming ISAS have entered into its scheduled orbit (JAXA) made the difficult decision Based on the Anomaly Experienced in March 2017. The successful start to terminate attempts to restore by Hitomi was developed. In of the ARASE mission is a testament communication with the X-ray addition, “town hall meetings” were to the dedication and skills across Astronomy Satellite ASTRO-H (also held to share the spirit and practice JAXA. known as HITOMI), which was of the action plan with all ISAS ISAS is currently operating six launched on February 17, 2016, due employees. The plan, which was satellites and space probes: ARASE, to the communication anomalies applied to launch preparations of Hayabusa2, HISAKI, AKATSUKI, that occurred on March 26, 2016. the geospace exploration satellite HINODE, and GEOTAIL. Asteroid Since that time, in consultation with ARASE, contributed to the successful Explorer Hayabusa2, which is experts inside as well as outside and stable operation of that satellite, currently on its planned trajectory JAXA, the Institute of Space and and will be applied to other projects towards the 162173 Ryugu asteroid Astronautical Science (ISAS) has such as the Smart Lander for under ion engine power, is equipped been making every possible effort Investigating Moon (SLIM). The plan- with new technologies for solar to determine what went wrong, and do-check-act (PDCA) cycle should system exploration such as long- what can be done to prevent this work to further refine both current distance communication using Ka- from happening again in the future. -

Securing Japan an Assessment of Japan´S Strategy for Space
Full Report Securing Japan An assessment of Japan´s strategy for space Report: Title: “ESPI Report 74 - Securing Japan - Full Report” Published: July 2020 ISSN: 2218-0931 (print) • 2076-6688 (online) Editor and publisher: European Space Policy Institute (ESPI) Schwarzenbergplatz 6 • 1030 Vienna • Austria Phone: +43 1 718 11 18 -0 E-Mail: [email protected] Website: www.espi.or.at Rights reserved - No part of this report may be reproduced or transmitted in any form or for any purpose without permission from ESPI. Citations and extracts to be published by other means are subject to mentioning “ESPI Report 74 - Securing Japan - Full Report, July 2020. All rights reserved” and sample transmission to ESPI before publishing. ESPI is not responsible for any losses, injury or damage caused to any person or property (including under contract, by negligence, product liability or otherwise) whether they may be direct or indirect, special, incidental or consequential, resulting from the information contained in this publication. Design: copylot.at Cover page picture credit: European Space Agency (ESA) TABLE OF CONTENT 1 INTRODUCTION ............................................................................................................................. 1 1.1 Background and rationales ............................................................................................................. 1 1.2 Objectives of the Study ................................................................................................................... 2 1.3 Methodology -
![Arxiv:0710.2934V2 [Astro-Ph] 17 Oct 2007](https://docslib.b-cdn.net/cover/5974/arxiv-0710-2934v2-astro-ph-17-oct-2007-1115974.webp)
Arxiv:0710.2934V2 [Astro-Ph] 17 Oct 2007
PASJ: Publ. Astron. Soc. Japan , 1–??, c 2018. Astronomical Society of Japan. A Tale Of Two Spicules: The Impact of Spicules on the Magnetic Chromosphere Bart De Pontieu1, Scott McIntosh2,3, Viggo H. Hansteen4,1, Mats Carlsson4 [email protected], [email protected], [email protected],[email protected] C.J. Schrijver1, T.D. Tarbell1, A.M. Title1, R.A. Shine1 [email protected], [email protected], [email protected], [email protected] Y. Suematsu5, S. Tsuneta5, Y. Katsukawa5, K. Ichimoto5, T. Shimizu6 S. Nagata7 [email protected],[email protected], [email protected], [email protected], [email protected], [email protected] 1Lockheed Martin Solar and Astrophysics Laboratory, Palo Alto, CA 94304, USA 2High Altitude Observatory, National Center for Atmospheric Research, PO Box 3000, Boulder, CO 80307, USA 3Department of Space Studies, Southwest Research Insititute, 1050 Walnut St, Suite 400, Boulder, CO 80302, USA 4Institute of Theoretical Astrophysics, University of Oslo, PB 1029 Blindern, 0315 Oslo Norway 5National Astronomical Observatory of Japan, Mitaka, Tokyo, 181-8588, Japan 6ISAS/JAXA, Sagamihara, Kanagawa, 229-8510, Japan 7Kwasan and Hida Observatories, Kyoto University,Yamashina, Kyoto, 607-8471, Japan (Received 2007 June 10; accepted accepted for Hinode special issue) Abstract We use high-resolution observations of the Sun in Ca II H (3968A)˚ from the Solar Optical Telescope on Hinode to show that there are at least two types of spicules that dominate the structure of the magnetic solar chromosphere. Both types are tied to the relentless magnetoconvective driving in the photosphere, but have very different dynamic properties. -

Abundances 164 ACE (Advanced Composition Explorer) 1, 21, 60, 71
Index abundances 164 CIR (corotating interaction region) 3, ACE (Advanced Composition Explorer) 1, 14À15, 32, 36À37, 47, 62, 108, 151, 21, 60, 71, 170À171, 173, 175, 177, 254À255 200, 251 energetic particles 63, 154 SWICS 43, 86 Climax neutron monitor 197 ACRs (anomalous cosmic rays) 10, 12, 197, CME (coronal mass ejection) 3, 14À15, 56, 258À259 64, 86, 93, 95, 123, 256, 268 CIRs 159 composition 268 pickup ions 197 open flux 138 termination shock 197, 211 comets 2À4, 11 active longitude 25 ComptonÀGetting effect 156 active region 25 convection equation tilt 25 diffusion 204 activity cycle (see also solar cycle) 1À2, corona 1À2 11À12 streamers 48, 63, 105, 254 Advanced Composition Explorer see ACE temperature 42 Alfve´n waves 116, 140, 266 coronal hole 30, 42, 104, 254, 265 AMPTE (Active Magnetospheric Particle PCH (polar coronal hole) 104, 126, 128 Tracer Explorer) mission 43, 197, coronal mass ejections see CME 259 corotating interaction regions see CIR anisotropy telescopes (AT) 158 corotating rarefaction region see CRR Cosmic Ray and Solar Particle Bastille Day see flares Investigation (COSPIN) 152 bow shock 10 cosmic ray nuclear composition (CRNC) butterfly diagram 24À25 172 cosmic rays 2, 16, 22, 29, 34, 37, 195, 259 Cassini mission 181 anomalous 195 CELIAS see SOHO charge state 217 CH see coronal hole composition 196, 217 CHEM 43 convection–diffusion model 213 282 Index cosmic rays (cont.) Energetic Particle Composition Experiment drift 101, 225 (EPAC) 152 force-free approximation 213 energetic particle 268 galactic 195 anisotropy 156, -

Temperature Variability in X-Ray Bright Points Observed with Hinode/XRT R
Temperature variability in X-ray bright points observed with Hinode/XRT R. Kariyappa, E. E. Deluca, S. H. Saar, L. Golub, Luc Damé, Alexei A. Pevtsov, B. A. Varghese To cite this version: R. Kariyappa, E. E. Deluca, S. H. Saar, L. Golub, Luc Damé, et al.. Temperature variability in X-ray bright points observed with Hinode/XRT. Astronomy and Astrophysics - A&A, EDP Sciences, 2011, 526, pp.A78. 10.1051/0004-6361/201014878. hal-00550486 HAL Id: hal-00550486 https://hal.archives-ouvertes.fr/hal-00550486 Submitted on 17 Jul 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A&A 526, A78 (2011) Astronomy DOI: 10.1051/0004-6361/201014878 & c ESO 2010 Astrophysics Temperature variability in X-ray bright points observed with Hinode/XRT R. Kariyappa1,2,E.E.DeLuca2,S.H.Saar2,L.Golub2,L.Damé3,A.A.Pevtsov4, and B. A. Varghese1 1 Indian Institute of Astrophysics, Bangalore 560034, India e-mail: [email protected] 2 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA, USA 3 LATMOS (Laboratoire Atmosphères, Milieux, Observations Spatiales), 11 boulevard d’Alembert, 78280 Guyancourt, France 4 National Solar Observatory, PO Box 62, Sunspot, NM 88349, USA Received 28 April 2010 / Accepted 10 November 2010 ABSTRACT Aims. -
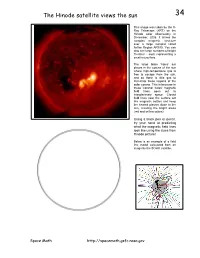
The Hinode Satellite Views the Sun 34
The Hinode satellite views the sun 34 This image was taken by the X- Ray Telescope (XRT) on the Hinode solar observatory in December, 2006. It shows the complex magnetic structure over a large sunspot called Active Region AR930. You can also see large numbers of bright 'freckles' - each representing a small micro-flare. The large black 'holes' are places in the corona of the sun where high-temperature gas is free to escape from the sun, and so there is little gas to illuminate these regions of the solar corona. This is because in these 'coronal holes' magnetic field lines open out to interplanetary space. Closed field lines near the surface act like magnetic bottles and keep the heated plasma close to the sun, creating the bright areas (red and yellow colors). Using a black pen or pencil, try your hand at predicting what the magnetic field lines look like using the clues from Hinode picture! Below is an example of a field line model calculated from an image by the SOHO satellite. Space Math http://spacemath.gsfc.nasa.gov 34 Answer Key: Students may come up with several different versions. The main thing to look for is that in the regions where the Hinode picture shows orange or yellow, students should draw loops of magnetism…like a bar magnet field….that are close-in to the solar surface. In the black regions (north pole) of sun and the large spot to the left of the sunspot (yellow), they should draw magnetic lines that start in the dark region but end outside the picture because they are continuing on into interplanetary space. -

JAXA's Planetary Exploration Plan
Planetary Exploration and International Collaboration Institute of Space and Astronautical Science Japan Aerospace Exploration Agency Yoshio Toukaku, Director for International Strategy and Coordination Naoya Ozaki, Assistant Professor, Dept of Spacecraft Engineering ISAS/JAXA September, 2019 The Path Japanese Planetary Exploration 1985 1995 2010 2018 Sakigake/ Nozomi Akatsuki BepiColombo Suisei MMO/MPO Comet flyby Planned and Venus Climate Mercury Orbiter launched Mars Orbiter orbiter Asteroid Sample Asteroid Sample Martian Moons Lunar probe Return Mission Return Mission explorer Hiten Hayabusa Hayabusa2 MMX 1992 2003 2014 2020s (TBD) Recent Science Missions HAYABUSA 2003-2010 HINODE(SOLAR-B)2006- KAGUYASELENE)2007-2009 Asteroid Explorer SolAr OBservAtion Lunar Exploration AKATSUKI 2010- Venus Meteorology IKAROS 2010 HisAki 2013 SolAr SAil PlAnetary atmosphere HAYABUSA2 2014-2020 Hitomi(ASTRO-H) 2016 ArAse (ERG) 2016 Asteroid Explorer X-Ray Astronomy Van Allen Belt proBe Hayabusa & Hayabusa 2 Asteroid Sample Return Missions “Hayabusa” spacecraft brought back the material of Asteroid Itokawa while establishing innovative ion engines. “Hayabusa2”, while utilizing the experience cultivated in “Hayabusa”, has arrived at the C type Asteroid Ryugu in order to elucidate the origin and evolution of the solar system and primordial materials that would have led to emergence of life. Hayabusa Hayabusa2 Target Itokawa Ryugu Launch 2003 2014 Arrival 2005 2018 Return 2010 2020 ©JAXA Asteroid Ryugu 6 Martian Moons eXploration (MMX) Sample return from Marian moon for detailed analysis. Strategic L-Class A key element in the ISAS roadmap for small body exploration. Phase A n Science Objectives 1. Origin of Mars satellites. - Captured asteroids? - Accreted debris resulting from a giant impact? 2. Preparatory processes enabling to the habitability of the solar system. -

Analysis of Small Scale Solar Magnetic Fields Using Hinode SOT/SP
Analysis of small scale solar magnetic fields using Hinode SOT/SP Dissertation for the award of the degree “Doctor rerum naturalium” (Dr.rer.nat.) of the Georg-August-Universität Göttingen within the doctoral program PROPHYS of the Georg-August University School of Science (GAUSS) submitted by David Bühler from Itzehoe Göttingen, 2013 Thesis Committee Prof. Dr. Sami K. Solanki Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany Prof. Dr. Stefan Dreizler Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Dr. Andreas Lagg Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany Members of the Examination Board Reviewer: Prof. Dr. Stefan Dreizler Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Second Reviewer: Prof. Dr. Sami K. Solanki Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany Additional Reviewer: Prof. Dr. Wolfgang Schmidt Kiepenheuer-Institut für Sonnenphysik, Albert-Ludwigs-Universität Freiburg, Germany Further members of the Examination Board: Prof. Dr. Manfred Schüssler Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany Prof. Dr. Laurent Gizon Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Prof. Dr. Wolfgang Glatzel Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Prof. Dr. Hardi Peter Max-Planck-Institut für Sonnensystemforschung, Katlenburg-Lindau, Germany Date of the oral examination: 7. November 2013 Bibliografische Information der Deutschen Nationalbibliothek Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie; detaillierte bibliografische Daten sind im Internet über http://dnb.d-nb.de abrufbar. ISBN 978-3-942171-78-6 uni-edition GmbH 2014 http://www.uni-edition.de c David Bühler This work is distributed under a Creative Commons Attribution 3.0 License Printed in Germany 3 Contents Summary 7 1 Introduction 9 1.1 Zeeman effect............................... -

Full-Sun Observations for Identifying the Source of the Slow Solar Wind
Full-Sun observations for identifying the source of the slow solar wind David H. Brooks1,*, Ignacio Ugarte-Urra1 & Harry P. Warren2 1 College of Science, George Mason University, 4400 University Drive, Fairfax, Virginia 22030, USA 2 Space Science Division, Naval Research Laboratory, 4555 Overlook Avenue SW, Washington, District Of Columbia 20375, USA * Correspondence to: [email protected] Present address: Hinode Team, ISAS/JAXA, 3-1-1 Yoshinodai, Chuo-ku, Sagamihara, Kanagawa 252-5210, Japan Abstract: Fast (>700 km s−1) and slow (~400 km s−1) winds stream from the Sun, permeate the heliosphere and influence the near-Earth environment. While the fast wind is known to emanate primarily from polar coronal holes, the source of the slow wind remains unknown. Here we identify possible sites of origin using a slow solar wind source map of the entire Sun, which we construct from specially designed, full- disk observations from the Hinode satellite, and a magnetic field model. Our map provides a full-Sun observation that combines three key ingredients for identifying the sources: velocity, plasma composition and magnetic topology and shows them as solar wind composition plasma outflowing on open magnetic field lines. The area coverage of the identified sources is large enough that the sum of their mass contributions can explain a significant fraction of the mass loss rate of the solar wind. Introduction Understanding the flow of energy and matter throughout the solar system is a fundamental goal of heliophysics, and identifying the solar sources of this flow would be a major step forward in achieving that objective.