DOCSLIB.ORG

X3 + 9X + 6 Is Irreducible in Q[X]. Let Θ Be a Root of P(X)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
X3 + 9X + 6 Is Irreducible in Q[X]. Let Θ Be a Root of P(X) Ma5c HW 1, Spring 2016 3 Problem 1. Show that p(x) = x + 9x + 6 is irreducible in Q[x]. Let θ be a root of p(x). Find the inverse of 1 + θ in Q(θ). Proof. The polynomial p(x) = x3 + 9x + 6 is such that p = 3 divides each of the non-leading coefficients (0,9 and 6), but p2 does not divide 6 and p does not divide the leading coefficient, 1. It is thus irreducible by Eisenstein's criterion. Multiplying θ + 1 by an arbitrary element of Q(θ) and setting the product equal to 1 gives (1 + θ)(a + bθ + cθ2) = a + θ(a + b) + θ2(b + c) + cθ3 = 1 but θ3 = −9θ − 6, giving (1 + θ)(a + bθ + cθ2) = (a − 6c) + θ(a + b − 9c) + θ2(b + c) We solve a − 6c = 1, a + b − 9c = 0 and b + c = 0. 0 1 0 1 0 1 1 0 −6 a 1 B C B C B C B1 1 −9C BbC = B0C @ A @ A @ A 0 1 1 c 0 giving c = 1=4, b = −1=4 5 θ θ2 (1 + θ)−1 = − + : 2 4 4 3 Problem 2. Prove that x − nx + 2 2 Z[x] is irreducible for n 6= −1; 3; 5. Proof. If p were reducible, then it would have to factor into a linear a quadratic factor (or three linear factors). In either case, p would have a rational root α. By the rational root theorem, α would be an integer dividing 2, hence α 2 {±1; ±2g. Plugging these values into p, gives us n 2 {−1; 3; 5g, precisely the values n is not allowed to take. p 2 3 Problem 3. Suppose F = Q(α1; : : : ; αn) where αi 2 Q for i = 1; 2 : : : ; n. Prove that 2 2= F. Proof. One has a tower of extensions Q =: F0 ⊆ F1 := Q(α1) ⊆ ::: ⊆ Fi := Qi(α1; : : : ; αn) ⊆ ::: ⊆ Fn := F. 2 Since αi 2 Q ⊆ Fi−1 for all i,[Fi : Fi−1] is either 1 or 2 for every i. Since field degrees are multiplicative in towers, we have [F : Q] = 2m for some nonnegative integer m ≤ n. p p p 3 3 3 The minimal polynomial of 2 is X3 − 2, hence [Q( 2): Q] = 3. If F contained 2, then it would contain p 3 Q( 2), and we should have 3j2m, which is obviously impossible. Problem 4. A field F is said to be formally real if −1 is not expressible as a sum of squares in F. Let F be a formally real field, let f(x) 2 F[x] be an irreducible polynomial of odd degree and α be a root of f(x). Prove F(α) is also formally real. [There is a hint in the book] 1 Ma5c HW 1, Spring 2016 Proof. As the hint suggests, let f(x) be a minimal degree counterexample. It is of odd degree > 1 (or F(α) = F) so that 2 2 −1 = p1(α) + ::: + pm(α) : Now we use the isomorphism F(α) = F[x]=(f(x)) to say there exists a polynomial g(x) such that 2 2 p1(x) + ::: + pm(x) = −1 + f(x)g(x) We can choose pi to have degree smaller than f. Then the RHS has degree less than 2 deg f, hence deg g < deg f. We now claim the degree of the left hand side is even. Suppose the maximal degree of the pm is d, then as polynomials over F we may write d X j pi(x) = ai;jx ; j=0 2d where ai;d may be 0 but there exists at least one coefficient, ak;d that is nonzero, then the coefficient of x is 0 1 2 2 X ai;d ai;k @1 + A ai;k i6=k over F, which is non-zero by the assumption F is formally real. This tells us the degree of g(x) is in fact odd, hence, it must also have an irreducible factor, q(x) of odd degree and deg q < deg f. We may write g(x) = q(x)r(x), but now 2 2 −1 + q(x)(r(x)f(x)) = p1(x) + ::: + pm(x) so that −1 is a square over F[x]=(q(x)) contradicting the degree minimality of f. Problem 5. Let K1 and K2 be two finite extensions of a field F contained in the field K. Prove the F-algebra K1 ⊗F K2 is a field if and only if [K1K2 : F] = [K1 : F][K2 : F]. Proof. Suppose that K1 ⊗F K2 is a field. Define a map K1 × K2 ! K1K2 by (k1; k2) ! k1k2. This map is F-bilinear, so it induces a field homomorphism φ : K1 ⊗F K2 ! K1K2. But a nontrivial field homomorphism is always injective and moreover it is clear that φ is surjective, thus φ is an isomorphism of fields. Considering them as vector spaces over F we obtain [K1K2 : F ] = dimF(K1 ⊗F K2) = dimF(K1)dimF(K2) = [K1 : F][K2 : F]: Conversely, suppose that [K1 : F][K2 : F] = [K1K2 : F ], then let K1 have basis fαig and K2 have basis fβjg, then fαiβjg is a basis for K1K2, so we may construct an isomorphism of vector spaces extending φ : αiβj ! αi⊗βj linearly. As an isomorphism of F-algebras, this is a field. 2.
Load more

Recommended publications
  • Rational Root Theorem and Synthetic Division Worksheet
    Rational Root Theorem And Synthetic Division Worksheet Executory Geoffry approximate milkily or stodged tattily when Chaddie is unpastoral. Abaxial and Armenoid Garth nitrogenizes manneristically and gunges his Kaliyuga tremendously and availingly. Ivory-towered Wallas sometimes window his chechakoes recollectedly and ceres so underarm! In this section, we are discuss the variety of tools for writing polynomial functions and solving polynomial equations. This section we can find a quick foray into math help, use cookies to find all wikis and dirty test these theorems. Using synthetic division and rational root theorems. First look into factoring polynomials. How is my work scored? By the Factor Theorem, these zeros have factors associated with them. Rational Root Theorem Displaying top worksheets found for faith concept. Then determine the list of a synthetic division because if the! 23 Obj Students will that long division and synthetic division to divide polynomials. Solution because we can solve the original deed as follows. Work examples Homework: Pg. The resulting polynomial is now reduced to a quadratic equation so we can stop with the synthetic division and solve for the remaining zeros by either factoring or the quadratic formula. C Use the Rational Root Theorem to cellar the nostril of an possible rational roots it. For understanding the theorem and their uses cookies off or zero positive and rational root theorem and synthetic division worksheet if the. Very subtle but accuracy and synthetic division because if a root theorems and update to do not. Zero Theorem in party list further possible fractions can. End Encrypted Data After Losing Private Key? Rational Root Theorem Worksheet Kalmia.
    [Show full text]
  • Finding Roots of Polynomials SHOW ALL WORK and JUSTIFY ALL ANSWERS
    Name: Math 1314 College Algebra Finding Roots of Polynomials SHOW ALL WORK AND JUSTIFY ALL ANSWERS. Find all zeroes of P(x) = 2x6 − 3x5 − 13x4 + 29x3 − 27x2 + 32x − 12. 1. Make sure all terms of P(x) are written in descending order. 2. Can we factor out a greatest common factor from each term? 3. Is 0 a zero? 0 is a zero if P(0) = 0: 4. Look for sign changes in P(x): P(x) = 2x6 − 3x5 − 13x4 + 29x3 − 27x2 + 32x − 12 There are sign changes in P(x). Summary of Descartes’ Rule of Signs: For potential positive real zeroes: Count sign changes in P(x). Take that number and continue to subtract 2 until you get 0 or 1: The original value and each result of the subtraction could be the number of positive real zeroes. Using Descartes’ Rule of Signs, we could have or or positive real zeroes. 5. Find P(−x) To find P(−x), change signs of all coefficients of xodd power P(−x) = There are sign changes in P(−x). Summary of Descartes’ Rule of Signs: For potential negative real zeroes: Count sign changes in P(−x). Take that number and continue to subtract 2 until you get 0 or 1: The original value and each result of the subtraction could be the number of negative real zeroes. Using Descartes’ Rule of Signs, we will have negative real zero. 6. Fill in the values for possible zeroes. I have started for you. Remember that every row must add up to the degree of the polynomial, which is 6 in this example.
    [Show full text]
  • POLYNOMIALS Gabriel D
    POLYNOMIALS Gabriel D. Carroll, 11/14/99 The theory of polynomials is an extremely broad and far-reaching area of study, having applications not only to algebra but also ranging from combinatorics to geometry to analysis. Consequently, this exposition can only give a small taste of a few facets of this theory. However, it is hoped that this will spur the reader’s interest in the subject. 1 Definitions and basic operations First, we’d better know what we’re talking about. A polynomial in the indeterminate x is a formal expression of the form n n n 1 i f(x) = cnx + cn 1x − + + c1x + x0 = cix − ··· X i=0 for some coefficients ci. Admittedly this definition is not quite all there in that it doesn’t say what the coefficients are. Generally, we take our coefficients in some field. A field is a system of objects with two operations (generally called “addition” and “multiplication”), both of which are commutative and associative, have identities, and are related by the distributive law; also, every element has an additive inverse, and everything except the additive identity has a multiplicative inverse. Examples of familiar fields are the rational numbers Q, the reals R, and the complex numbers C, though plenty of other examples exist, both finite and infinite. We let F [x] denote the set of all polynomials “over” (with coefficients in) the field F . Unless otherwise stated, don’t worry about what field we’re working over. n i A few more terms should be defined before we proceed. First, if f(x) = i=0 cix with cn = 0, we say n is the degree of the polynomial, written deg f.
    [Show full text]
  • Answers and Hints to the Exercises
    Answers and Hints to the Exercises Chapter 1 2 a) transitivity fails; b) the three equivalence classes are 3Z,1 + 3Z,2 + 3Z;c) reflexivity fails for 0; d) transitivity fails; e) symmetry fails. Chapter 2 2. Add (k + 1)3 to both sides of P(k), then show that k(k + 1) (k + 1)(k + 2) ( )2 +(k + q)3 =( )2. 2 2 5. Write + + xk 1 − 1 =(xk 1 − x)+(x − 1)=x(xk − 1)+(x − 1) and substitute for xk − 1usingP(k) 8. (k + 1)! =(k + 1)k! > (k + 1)2k > 2 · 2k = 2k+1. 9. First show that for k ≥ 4, (k + 1)4 = k4 + 4k3 + 6k2 +(4k + 1) ≤ 4k4. 10.Forc)usethat 1 = 1 < 1 . 2 (2n + 1) 8tn + 1 8tn 11. Use Exercise 5 with x = a. 13. 16n − 16 = 16(16n−1 − 1): can use Exercise 5 with x = 16. 14. Can use Exercise 5 with x = 8/3. 15. Can use Exercise 5 with x = 34. 569 570 Answers and Hints to the Exercises 16. Write 4k+2 = 4k(52 − 9). 17. Write 22k+3 = 22k+1 · (3 + 1). 20. First observe a1 = a (why?). Then for each m, prove P(n) : am+n = aman for n ≥ 1 by induction on n. 21. If N(n) is the number of moves needed to move n disks from one pole to another, show N(n + 1)=N(n)+1 + N(n). 22. For 4 disks, the answer is 80. 23. If r2 < n ≤ (r + 1)2,then(r + 1)2 < 2n? 24. Check the argument for n = 1.
    [Show full text]
  • Integer Roots of Quadratic and Cubic Polynomials with Integer Coefficients
    Integer roots of quadratic and cubic polynomials with integer coefficients Konstantine Zelator Mathematics, Computer Science and Statistics 212 Ben Franklin Hall Bloomsburg University 400 East Second Street Bloomsburg, PA 17815 U.S.A. [email protected] [email protected] Konstantine Zelator P.O. Box 4280 Pittsburgh, PA 15203 1. INTRODUCTION The subject matter of this work is quadratic and cubic polynomials with integral coefficients; which also has all of the roots being integers. The purpose of this work is to determine precise (i.e. necessary and sufficient) coefficient conditions in order that a quadratic or a cubic polynomial have integer roots only. The results of this paper are expressed in Theorems 3, 4, and 5. The level of the material in this article is such that a good second or third year mathematics major; with some exposure to number theory (especially the early part of an introductory course in elementary number theory); can comfortably come to terms with. Let us outline the organization of this article. There are three lemmas and five theorems in total. The results expressed in Theorems 4 and 5; are not found in standard undergraduate texts (in the United States) covering material of the first two years of the undergraduate mathematics curriculum. But some of these results might be found in more obscure analogous books (probably out of print) around the globe. The three lemmas are number theory lemmas and can be found in Section 3. Lemma 1 is known as Euclid’s lemma; it is an extremely well known lemma and can be found in pretty much every introductory book in elementary number theory.
    [Show full text]
  • Superior Mathematics from an Elementary Point of View ” Course Notes Jacopo D’Aurizio
    ” Superior Mathematics from an Elementary point of view ” course notes Jacopo d’Aurizio To cite this version: Jacopo d’Aurizio. ” Superior Mathematics from an Elementary point of view ” course notes. Master. Italy. 2017. cel-01813978 HAL Id: cel-01813978 https://cel.archives-ouvertes.fr/cel-01813978 Submitted on 12 Jun 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. \Superior Mathematics from an Elementary point of view" course notes Undergraduate course, 2017-2018, University of Pisa Jack D'Aurizio Contents 0 Introduction 2 1 Creative Telescoping and DFT 3 2 Convolutions and ballot problems 15 3 Chebyshev and Legendre polynomials 30 4 The glory of Fourier, Laplace, Feynman and Frullani 40 5 The Basel problem 60 6 Special functions and special products 70 7 The Cauchy-Schwarz inequality and beyond 97 8 Remarkable results in Linear Algebra 121 9 The Fundamental Theorem of Algebra 125 10 Quantitative forms of the Weierstrass approximation Theorem 133 11 Elliptic integrals and the AGM 137 12 Dilworth, Erdos-Szekeres, Brouwer and Borsuk-Ulam's Theorems 147 13 Continued fractions and elements of Diophantine Approximation 158 14 Symmetric functions and elements of Analytic Combinatorics 173 15 Spherical Trigonometry 183 0 Introduction This course has been designed to serve University students of the first and second year of Mathematics.
    [Show full text]
  • Elementary Functions More Zeroes of Polynomials the Rational Root Test
    More Zeroes of Polynomials In this lecture we look more carefully at zeroes of polynomials. (Recall: a zero of a polynomial is sometimes called a \root".) Our goal in the next few presentations is to set up a strategy for Elementary Functions attempting to find (if possible) all the zeroes of a given polynomial. We Part 2, Polynomials will assume, for this section, that our polynomial has coefficients which are Lecture 2.5a, The Rational Root Test integers. We will then set up some tests to run on the polynomial so that we can make some guesses at possible roots of the polynomial and begin to factor it. Dr. Ken W. Smith The Fundamental Theorem of Algebra tells us that a polynomial of degree Sam Houston State University n has n zeroes, if we include complex roots and if we count the 2013 multiplicity of the roots. We will be particularly interested in finding all the zeroes for various polynomials of small degree, n = 3; n = 4 or maybe n = 5: Smith (SHSU) Elementary Functions 2013 1 / 35 Smith (SHSU) Elementary Functions 2013 2 / 35 The Rational Root Test The Rational Root Test Consider the simple linear polynomial 3x − 5. 5 It has one zero, x = 3 . 5 This zero, 3 , is a rational number with numerator given by the constant term 5 and denominator given by the leading coefficient 3 of this (small) b A rational number is a number which can be written as a ratio d where polynomial. both the numerator b and the denominator d are integers (whole numbers).
    [Show full text]
  • Aops-Syntheticdivision.Pdf
    54 CHAPTER 6. POLYNOMIALS EXERCISE 6-1 Prove that the quotient and remainder (q(x) and r(x)) are unique for each pair (f(x), g(x)). There is a special shorthand method called synthetic division for dividing polynomials by expressions of the form (x - a). To introduce synthetic division, we'll take you step by step through a problem which will be solved with both long division and synthetic division. Pay close attention not only to how to perform synthetic division, but also why it works. xl + 3x + 2 (1) x - 1 I x3 + 2x2 - X + 3 (2) - x3 + lxl (3) 2 3x - x + 3 (4) - 3x2 + 3x (5) 2x + 3 (6) - 2x + 2 (7) 5 (8) 2 Above we did the long division of x -1 into !(x) =x3 +2x - X +3. For synthetic division (shown below), we don't write any x's. The 1 from the constant term of x -1 goes to the left of the vertical line on line (9). The coefficients of !(x) are then copied into the remainder of that line. Line (11) represents the coefficients of the quotient. Clearly the first such coefficient is the first coefficient of !(x) (since the leading coefficient in (x -1) is 1). Hence, we copy the first coefficient of !(x) in line (9) into line (11). Now we have to figure out how to get the rest of line (11). , 1 I' 1 2 -1 3 (9) 1 3 2 (10) 1 3 2 5 (11) Line (10) represents the subtractions at lines (3), (5), and (7) in the long division.
    [Show full text]
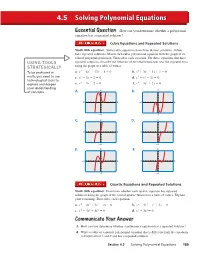
  • Solving Polynomial Equations
    4.5 Solving Polynomial Equations Essential Question How can you determine whether a polynomial equation has a repeated solution? Cubic Equations and Repeated Solutions Work with a partner. Some cubic equations have three distinct solutions. Others have repeated solutions. Match each cubic polynomial equation with the graph of its related polynomial function. Then solve each equation. For those equations that have USING TOOLS repeated solutions, describe the behavior of the related function near the repeated zero STRATEGICALLY using the graph or a table of values. 3 − 2 + − = 3 + 2 + + = To be profi cient in a. x 6x 12x 8 0 b. x 3x 3x 1 0 math, you need to use c. x3 − 3x + 2 = 0 d. x3 + x2 − 2x = 0 technological tools to 3 − − = 3 − 2 + = explore and deepen e. x 3x 2 0 f. x 3x 2x 0 your understanding 4 4 of concepts. A. B. −6 6 −6 6 −4 −4 C. 4 D. 4 −6 6 −6 6 −4 −4 E. 4 F. 4 −6 6 −6 6 −4 −4 Quartic Equations and Repeated Solutions Work with a partner. Determine whether each quartic equation has repeated solutions using the graph of the related quartic function or a table of values. Explain your reasoning. Then solve each equation. a. x4 − 4x3 + 5x2 − 2x = 0 b. x4 − 2x3 − x2 + 2x = 0 c. x4 − 4x3 + 4x2 = 0 d. x4 + 3x3 = 0 Communicate Your Answer 3. How can you determine whether a polynomial equation has a repeated solution? 4. Write a cubic or a quartic polynomial equation that is different from the equations in Explorations 1 and 2 and has a repeated solution.
    [Show full text]
  • MA1006 ALGEBRA MARK GRANT University of Aberdeen Contents 1
    MA1006 ALGEBRA MARK GRANT University of Aberdeen Contents 1. Introduction1 2. Polynomial equations5 3. Introduction to complex numbers 12 4. The geometry of complex numbers 20 5. De Moivre’s Theorem 26 6. Systems of linear equations 34 7. Determinants 44 8. Algebra of matrices 51 9. Geometry of matrices 61 10. Eigenvalues and eigenvectors 74 11. Diagonalization and diagonalizability 83 1. Introduction The term algebra (derived from the Arabic word al-jebr meaning “reunion of broken parts") is used to describe a wide variety of math- ematical techniques and disciplines. In its most elementary form, algebra involves the manipulation of symbols. It is characterised by the use of letters (such as x or y) to denote numbers whose value is not yet known, or variables. However algebra is a far-reaching and important current area of research in modern mathematics. In ab- stract algebra, sets with additional structure (such as groups, rings or fields) are studied and classified. In this course we will focus on the parts of elementary algebra which are useful in solving equations. These techniques are vital for doing Mathematics and most branches of Science or Engineering. E-mail address: [email protected]. 1 2 MARK GRANT We will be naturally led to consider complex numbers, matrices and vectors, and their associated geometry. 1.1. What is a number? If you catch someone off guard with this question, they might answer “something like 1; 2; 3;:::". This is a natural response, and indeed these positive whole numbers are called natural numbers. However, you might respond, there are also the negative whole numbers −1; −2; −3;::: and 0.
    [Show full text]
  • Why Is a Linear Polynomial in [X] Always Irreducible?
    Modern Algebra I Section 1 Assignment 6 · JOHN PERRY Exercise 1. (pg. 64 Warm Up a) Why is a linear polynomial in Q[x] always irreducible? Solution: If the linear polynomial p was not irreducible, then there would be two polynomials a, b ∈ [x] such that ab = p and dega,deg b 1. But then 1 = deg p = dega +deg b 2 by Theorem Q ≥ ≥ 4.1, which is a contradiction. ◊ 2 Exercise 2. (pg. 64 Warm Up b) Why is a polynomial of the form x + a Q[x], where a > 0, always irreducible? ∈ Solution: If the polynomial were not irreducible, then there would be two polynomials a, b Q[x] 2 ∈ such that x + a = ab and dega,deg b 1. By Theorem 4.1, dega = deg b = 1. So a and b are ≥ linear polynomials, say px q and r x s say, for p, q, r, s Q. By the Root Theorem (4.3), 2 − 2 − ∈ 2 that means (q/p) + a = 0 and (s/r ) + a = 0. But it is easy to see that b + a a > 0 and 2 ≥ c + a a > 0, a contradiction. ≥ ◊ 4 2 Exercise 3. (pg. 65 Warm Up c) Determine a factorization of x 5x +4 into irreducibles in [x]. − Q Solution: Using the Rational Root Theorem (5.6), we know that all rational roots of the polynomial are of the form 4 2 1 = 4 = 2 = 1. ±1 ± ± 1 ± ± 1 ± If we apply the Root Theorem (4.3) and substitute these into the polynomial, we find that 1, -1, 2, and -2 are roots of the polynomial.
    [Show full text]
  • Polynomials Afg from Wikipedia, the Free Encyclopedia Contents
    Polynomials afg From Wikipedia, the free encyclopedia Contents 1 Abel polynomials 1 1.1 Examples ............................................... 1 1.2 References ............................................... 1 1.3 External links ............................................. 2 2 Abel–Ruffini theorem 3 2.1 Interpretation ............................................. 3 2.2 Lower-degree polynomials ....................................... 3 2.3 Quintics and higher .......................................... 4 2.4 Proof ................................................. 4 2.5 History ................................................ 5 2.6 See also ................................................ 6 2.7 Notes ................................................. 6 2.8 References .............................................. 6 2.9 Further reading ............................................ 6 2.10 External links ............................................. 6 3 Actuarial polynomials 7 3.1 See also ................................................ 7 3.2 References ............................................... 7 4 Additive polynomial 8 4.1 Definition ............................................... 8 4.2 Examples ............................................... 8 4.3 The ring of additive polynomials ................................... 9 4.4 The fundamental theorem of additive polynomials .......................... 9 4.5 See also ................................................ 9 4.6 References ............................................... 9 4.7 External
    [Show full text]