DOCSLIB.ORG

Estimating the Mean and Variance of a Normal Distribution

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Estimating the Mean and Variance of a Normal Distribution Estimating the Mean and Variance of a Normal Distribution Learning Objectives After completing this module, the student will be able to • explain the value of repeating experiments • explain the role of the law of large numbers in estimating population means • describe the effect of increasing the sample size or reducing measurement errors or other sources of variability Knowledge and Skills • Properties of the arithmetic mean • Estimating the mean of a normal distribution • Law of Large Numbers • Estimating the Variance of a normal distribution • Generating random variates in EXCEL Prerequisites 1. Calculating sample mean and arithmetic average 2. Calculating sample standard variance and standard deviation 3. Normal distribution Citation: Neuhauser, C. Estimating the Mean and Variance of a Normal Distribution. Created: September 9, 2009 Revisions: Copyright: © 2009 Neuhauser. This is an open‐access article distributed under the terms of the Creative Commons Attribution Non‐Commercial Share Alike License, which permits unrestricted use, distribution, and reproduction in any medium, and allows others to translate, make remixes, and produce new stories based on this work, provided the original author and source are credited and the new work will carry the same license. Funding: This work was partially supported by a HHMI Professors grant from the Howard Hughes Medical Institute. Page 1 Pretest 1. Laura and Hamid are late for Chemistry lab. The lab manual asks for determining the density of solid platinum by repeating the measurements three times. To save time, they decide to only measure the density once. Explain the consequences of this shortcut. 2. Tom and Bao Yu measured the density of solid platinum three times: 19.8, 21.4, and 21.9 g/cm3. Determine the arithmetic average of these three measurements accurate to three decimal places. 3. The following graphs are densities of probability distributions. Which represent the density of a normal distribution? (a) (b) (c) 0.5 2.5 0.35 0.45 0.3 0.4 2 0.25 0.35 0.3 1.5 0.2 0.25 0.15 0.2 1 0.15 0.1 0.1 0.5 0.05 0.05 0 0 0 0 2 4 6 0 2 4 6 0 2 4 6 t t 4. Which two parameters are typically used to describe the normal distribution? a. Median b. Variance c. Standard deviation d. Mean 5. Suppose X is normally distributed with mean 3 and standard deviation 1, that is, XN∼ (3,1) . Use EXCEL to (a) find PX(3)> , (b) find PX(1< < 4) , and (c) determine a so that PX(>= a ) 0.74 . Citation: Neuhauser, C. Estimating the Mean and Variance of a Normal Distribution. Created: September 9, 2009 Revisions: Copyright: © 2009 Neuhauser. This is an open‐access article distributed under the terms of the Creative Commons Attribution Non‐Commercial Share Alike License, which permits unrestricted use, distribution, and reproduction in any medium, and allows others to translate, make remixes, and produce new stories based on this work, provided the original author and source are credited and the new work will carry the same license. Funding: This work was partially supported by a HHMI Professors grant from the Howard Hughes Medical Institute. Page 2 Estimating the Mean of a Normally Distributed Population Suppose an experiment is repeated n times under identical conditions. Denote by xi ,1,2,,in= … the outcome of each individual experiment. The arithmetic average xn is calculated n xx12+++… xn 1 xni==∑x nni=1 When outcomes are not all distinct, we can count the number of times each value occurs: Suppose again that an experiment is repeated n times under identical conditions. But now, we assume that there are only k distinct values x j , jk= 1,2,..., , and that x j occurs fj times. Then the arithmetic average xn is calculated 11k xnkkjj=+++=()xf11 xf 22 ... xf∑ xf nnj=1 Example Suppose that the following data represent the ages of patients in a study: 17, 19, 19, 20, 21, 24, 26, 26, 26, and 27. We find for the arithmetic average 17+++++++++ 19 19 20 21 24 26 26 26 27 225 x ===22.5 10 10 10 Since some of the values occur more than twice, we can also use the frequency distribution: xj 17 19 20 21 24 26 27 fj 1 2 1 1 1 3 1 For the arithmetic average we find 1225 x =++++++==()(17)(1) (19)(2) (20)(1) (21)(1) (24)(1) (26)(3) (27)(1) 22.5 10 10 10 Citation: Neuhauser, C. Estimating the Mean and Variance of a Normal Distribution. Created: September 9, 2009 Revisions: Copyright: © 2009 Neuhauser. This is an open‐access article distributed under the terms of the Creative Commons Attribution Non‐Commercial Share Alike License, which permits unrestricted use, distribution, and reproduction in any medium, and allows others to translate, make remixes, and produce new stories based on this work, provided the original author and source are credited and the new work will carry the same license. Funding: This work was partially supported by a HHMI Professors grant from the Howard Hughes Medical Institute. Page 3 In‐class Activity We will explore the properties of the arithmetic mean when measurements are taken from a normal distribution. Open the first tab (Explore 1) on the accompanying spreadsheet. Column B has 100 random variates from a normal distribution with mean 3 and variance 1. Recall that the function “=NORMINV(probability,mean,standard_dev)” returns the inverse of the normal cumulative distribution for the specified mean and standard deviation. Column C calculates the cumulative sum and Column D has the corresponding arithmetic averages. The Figure plots Column D against Column A. Use the F9 key to explore the arithmetic average. What do you observe? Theory In Explore 1, you observed that the arithmetic mean stabilizes around the mean of the normal distribution, regardless of the variance, as you increase the sample size. This is a consequence of the Law of Large Numbers. While we do not yet have the background to completely understand its mathematical formulation, we will give it here anyway so that you can see how a mathematical result expressing this property is formulated. We will come back to this result later in the course when we have more background. Law of Large Numbers If XX12,,,… Xn are independent and identically distributed with EX||i < ∞ , then as n tends to infinity, Xn converges to EX1 in probability. Problems 1. A random variate is a particular outcome of a random variable. Assume that random variates are drawn repeatedly from a normal distribution with mean 4 and variance 9. If you calculated the arithmetic average for a large number of variates from this distribution, what would you expect the arithmetic average to be close to? 2. The Law of Large Numbers holds quite generally. Without going more deeply into the theory, can you guess the answer to the following problem? Suppose you repeatedly tossed a biased coin where heads occur with probability 0.2. What percentage of time would you expect to see heads? Based on our observations in Explore 1, we conclude that the mean of a normal distribution can be estimated by repeatedly sampling from the normal distribution and calculating the arithmetic average of the sample. This arithmetic average serves as an estimate for the mean of the normal distribution. Citation: Neuhauser, C. Estimating the Mean and Variance of a Normal Distribution. Created: September 9, 2009 Revisions: Copyright: © 2009 Neuhauser. This is an open‐access article distributed under the terms of the Creative Commons Attribution Non‐Commercial Share Alike License, which permits unrestricted use, distribution, and reproduction in any medium, and allows others to translate, make remixes, and produce new stories based on this work, provided the original author and source are credited and the new work will carry the same license. Funding: This work was partially supported by a HHMI Professors grant from the Howard Hughes Medical Institute. Page 4 Properties of the Arithmetic Average Explore 2 When you compare the arithmetic averages of 100 random variates in Explore 1, you will realize that different runs of the simulation result in slightly different averages. Arithmetic averages are random variables and we will explore their distribution as a function of the sample size. Again, we will use normally distributed random variables. A simulation is set up under the tab Explore 2 that simulates arithmetic averages of normally distributed random variables. We vary the sample sizes. Details are explained in the spreadsheet. Use the F9 key to explore the effect of the sample size on the arithmetic average. What do you observe? Explore 3 The variation in the arithmetic mean comes from the fact that the random variates in each sample vary from run to run. The more the random variates vary, the more the arithmetic mean varies. The degree of variation is described by the standard deviation. To explore the effect of the variation, we simulate arithmetic means for two different scenarios in the spreadsheet under tab Explore 3: in one simulation, we calculate arithmetic means for random variates that are normally distributed with mean 3 and standard deviation 1; in the second scenario, we calculate arithmetic means for random variates that are normally distributed with mean 3 and standard deviation 0.5. Details are explained in the spreadsheet. Use the F9 key to explore the effect of the standard deviation on the arithmetic average. What do you observe? Problems (cont.) 3. Based on your observations in Explore 2 and 3, what is the effect on the arithmetic mean when you (a) increase sample size and (b) reduce variation. What does this imply for experiments? Citation: Neuhauser, C.
Load more

Recommended publications
  • Applied Biostatistics Mean and Standard Deviation the Mean the Median Is Not the Only Measure of Central Value for a Distribution
    Health Sciences M.Sc. Programme Applied Biostatistics Mean and Standard Deviation The mean The median is not the only measure of central value for a distribution. Another is the arithmetic mean or average, usually referred to simply as the mean. This is found by taking the sum of the observations and dividing by their number. The mean is often denoted by a little bar over the symbol for the variable, e.g. x . The sample mean has much nicer mathematical properties than the median and is thus more useful for the comparison methods described later. The median is a very useful descriptive statistic, but not much used for other purposes. Median, mean and skewness The sum of the 57 FEV1s is 231.51 and hence the mean is 231.51/57 = 4.06. This is very close to the median, 4.1, so the median is within 1% of the mean. This is not so for the triglyceride data. The median triglyceride is 0.46 but the mean is 0.51, which is higher. The median is 10% away from the mean. If the distribution is symmetrical the sample mean and median will be about the same, but in a skew distribution they will not. If the distribution is skew to the right, as for serum triglyceride, the mean will be greater, if it is skew to the left the median will be greater. This is because the values in the tails affect the mean but not the median. Figure 1 shows the positions of the mean and median on the histogram of triglyceride.
    [Show full text]
  • Business Statistics Unit 4 Correlation and Regression.Pdf
    RCUB, B.Com 4 th Semester Business Statistics – II Rani Channamma University, Belagavi B.Com – 4th Semester Business Statistics – II UNIT – 4 : CORRELATION Introduction: In today’s business world we come across many activities, which are dependent on each other. In businesses we see large number of problems involving the use of two or more variables. Identifying these variables and its dependency helps us in resolving the many problems. Many times there are problems or situations where two variables seem to move in the same direction such as both are increasing or decreasing. At times an increase in one variable is accompanied by a decline in another. For example, family income and expenditure, price of a product and its demand, advertisement expenditure and sales volume etc. If two quantities vary in such a way that movements in one are accompanied by movements in the other, then these quantities are said to be correlated. Meaning: Correlation is a statistical technique to ascertain the association or relationship between two or more variables. Correlation analysis is a statistical technique to study the degree and direction of relationship between two or more variables. A correlation coefficient is a statistical measure of the degree to which changes to the value of one variable predict change to the value of another. When the fluctuation of one variable reliably predicts a similar fluctuation in another variable, there’s often a tendency to think that means that the change in one causes the change in the other. Uses of correlations: 1. Correlation analysis helps inn deriving precisely the degree and the direction of such relationship.
    [Show full text]
  • Beating Monte Carlo
    SIMULATION BEATING MONTE CARLO Simulation methods using low-discrepancy point sets beat Monte Carlo hands down when valuing complex financial derivatives, report Anargyros Papageorgiou and Joseph Traub onte Carlo simulation is widely used to ods with basic Monte Carlo in the valuation of alised Faure achieves accuracy of 10"2 with 170 M price complex financial instruments, and a collateraliscd mortgage obligation (CMO). points, while modified Sobol uses 600 points. much time and money have been invested in We found that deterministic methods beat The Monte Carlo method, on the other hand, re• the hope of improving its performance. How• Monte Carlo: quires 2,700 points for the same accuracy, ever, recent theoretical results and extensive • by a wide margin. In particular: (iii) Monte Carlo tends to waste points due to computer testing indicate that deterministic (i) Both the generalised Faure and modified clustering, which severely compromises its per• methods, such as simulations using Sobol or Sobol methods converge significantly faster formance when the sample size is small. Faure points, may be superior in both speed than Monte Carlo. • as the sample size and the accuracy de• and accuracy. (ii) The generalised Faure method always con• mands grow. In particular: Tn this paper, we refer to a deterministic verges at least as fast as the modified Sobol (i) Deterministic methods are 20 to 50 times method by the name of the sequence of points method and often faster. faster than Monte Carlo (the speed-up factor) it uses, eg, the Sobol method. Wc tested the gen• (iii) The Monte Carlo method is sensitive to the even with moderate sample sizes (2,000 de• eralised Faure sequence due to Tezuka (1995) initial seed.
    [Show full text]
  • Lecture 3: Measure of Central Tendency
    Lecture 3: Measure of Central Tendency Donglei Du ([email protected]) Faculty of Business Administration, University of New Brunswick, NB Canada Fredericton E3B 9Y2 Donglei Du (UNB) ADM 2623: Business Statistics 1 / 53 Table of contents 1 Measure of central tendency: location parameter Introduction Arithmetic Mean Weighted Mean (WM) Median Mode Geometric Mean Mean for grouped data The Median for Grouped Data The Mode for Grouped Data 2 Dicussion: How to lie with averges? Or how to defend yourselves from those lying with averages? Donglei Du (UNB) ADM 2623: Business Statistics 2 / 53 Section 1 Measure of central tendency: location parameter Donglei Du (UNB) ADM 2623: Business Statistics 3 / 53 Subsection 1 Introduction Donglei Du (UNB) ADM 2623: Business Statistics 4 / 53 Introduction Characterize the average or typical behavior of the data. There are many types of central tendency measures: Arithmetic mean Weighted arithmetic mean Geometric mean Median Mode Donglei Du (UNB) ADM 2623: Business Statistics 5 / 53 Subsection 2 Arithmetic Mean Donglei Du (UNB) ADM 2623: Business Statistics 6 / 53 Arithmetic Mean The Arithmetic Mean of a set of n numbers x + ::: + x AM = 1 n n Arithmetic Mean for population and sample N P xi µ = i=1 N n P xi x¯ = i=1 n Donglei Du (UNB) ADM 2623: Business Statistics 7 / 53 Example Example: A sample of five executives received the following bonuses last year ($000): 14.0 15.0 17.0 16.0 15.0 Problem: Determine the average bonus given last year. Solution: 14 + 15 + 17 + 16 + 15 77 x¯ = = = 15:4: 5 5 Donglei Du (UNB) ADM 2623: Business Statistics 8 / 53 Example Example: the weight example (weight.csv) The R code: weight <- read.csv("weight.csv") sec_01A<-weight$Weight.01A.2013Fall # Mean mean(sec_01A) ## [1] 155.8548 Donglei Du (UNB) ADM 2623: Business Statistics 9 / 53 Will Rogers phenomenon Consider two sets of IQ scores of famous people.
    [Show full text]
  • “Mean”? a Review of Interpreting and Calculating Different Types of Means and Standard Deviations
    pharmaceutics Review What Does It “Mean”? A Review of Interpreting and Calculating Different Types of Means and Standard Deviations Marilyn N. Martinez 1,* and Mary J. Bartholomew 2 1 Office of New Animal Drug Evaluation, Center for Veterinary Medicine, US FDA, Rockville, MD 20855, USA 2 Office of Surveillance and Compliance, Center for Veterinary Medicine, US FDA, Rockville, MD 20855, USA; [email protected] * Correspondence: [email protected]; Tel.: +1-240-3-402-0635 Academic Editors: Arlene McDowell and Neal Davies Received: 17 January 2017; Accepted: 5 April 2017; Published: 13 April 2017 Abstract: Typically, investigations are conducted with the goal of generating inferences about a population (humans or animal). Since it is not feasible to evaluate the entire population, the study is conducted using a randomly selected subset of that population. With the goal of using the results generated from that sample to provide inferences about the true population, it is important to consider the properties of the population distribution and how well they are represented by the sample (the subset of values). Consistent with that study objective, it is necessary to identify and use the most appropriate set of summary statistics to describe the study results. Inherent in that choice is the need to identify the specific question being asked and the assumptions associated with the data analysis. The estimate of a “mean” value is an example of a summary statistic that is sometimes reported without adequate consideration as to its implications or the underlying assumptions associated with the data being evaluated. When ignoring these critical considerations, the method of calculating the variance may be inconsistent with the type of mean being reported.
    [Show full text]
  • Notes on Calculating Computer Performance
    Notes on Calculating Computer Performance Bruce Jacob and Trevor Mudge Advanced Computer Architecture Lab EECS Department, University of Michigan {blj,tnm}@umich.edu Abstract This report explains what it means to characterize the performance of a computer, and which methods are appro- priate and inappropriate for the task. The most widely used metric is the performance on the SPEC benchmark suite of programs; currently, the results of running the SPEC benchmark suite are compiled into a single number using the geometric mean. The primary reason for using the geometric mean is that it preserves values across normalization, but unfortunately, it does not preserve total run time, which is probably the figure of greatest interest when performances are being compared. Cycles per Instruction (CPI) is another widely used metric, but this method is invalid, even if comparing machines with identical clock speeds. Comparing CPI values to judge performance falls prey to the same prob- lems as averaging normalized values. In general, normalized values must not be averaged and instead of the geometric mean, either the harmonic or the arithmetic mean is the appropriate method for averaging a set running times. The arithmetic mean should be used to average times, and the harmonic mean should be used to average rates (1/time). A number of published SPECmarks are recomputed using these means to demonstrate the effect of choosing a favorable algorithm. 1.0 Performance and the Use of Means We want to summarize the performance of a computer; the easiest way uses a single number that can be compared against the numbers of other machines.
    [Show full text]
  • Weighted Arithmetic Mean in Ancient India ̊І ˨Ͻ˨Ξϑі˨ ͬϞͻ˨Ξ ̙Ϟϑϑ˨
    ͖͑χϑΎξ͖̐˨ͱ Weighted Arithmetic Mean in Ancient India ̊І ˨ͻ˨ξϑІ˨ ͬϟͻ˨ξ ̙ϟϑϑ˨ ߝ vȘɾɟȩƇʕżɾǞȩȘ Òׯ»× ŁÁÎ »ÒÜÎł Á¨ ×­¯Ò Ŋ¼×ε ×¼¼ìŌ ŁµÒÁ µµ ŊåΩŌł Ò³Ò ×Á ¯¼×¯¨ì ×­× ×ì̯µ ÁÎ ¼×ε åµÜ Á¨ ×­ ¯Ò×ίÜׯÁ¼ æ­¯­ æÁܵį ¯¼ ÒÁ» Ò¼Òį ¯×Ò ůŬ ūŬŬŷ ŹŬŮŨŹū ×­× VĮĮ E­µ¼Á¯Ò ­ ¨ÁÎ ×­ ËÐ ÇÅÇ˶Ð}ЪÜĮ a­ žÎ¯×­»×¯ E¼į E¯¼ ¼ EÁ »×­»×¯µ ¼ Ò¯¼×¯¨¯ ¯¼×µµ× Á¨ ¼¯¼× Î ×­Î Ò׼Π»ÒÜÎÒ Á¨ ¼×ε ×¼¼ì ÜÒ ¯¼ 2¼¯ ¯Ò ëÌÎÒÒ ¯¼ ×­ åÎì ¼» Z}¶­¨ã ×­× ­ Ò×ׯÒׯÒĮ a­ÜÒį ×­ ÌÎ¯Ò Î¯×­»×¯ ŁÎ×­Îį µ©Î¯ł a­ÁÒ ¨ÁÎ ×­ ±ÁÜμµ Á¼ Ò×ׯÒ×¯Ò ×­× ­ ¨Áܼ ¯¼ ĂĊĄĄĮ 2¼ ¨Áλܵ ŁĂł ¯Ò å¯æ ¯¼ Ò×ׯÒ×¯Ò Ò ¼ Òׯ»× Á¨ ×­ ¼×ε ×¼¼ì Á¨ ¯Ò×ίÜׯÁ¼Į ×­ ¯¼Ü©Üε ¯×Áίµ Á¨ Z}¶­¨ã [1]į Ò µÒÁ ¯¼ ­¯Ò µÎ× Îׯµ Ŋp­ì \×ׯÒׯÒĵŌ [2]į E­µ¼Á¯Ò ­¯©­µ¯©­×Ò ÒÁ» Á¨ p­¼ ×­ n ÍÜ¼×¯×¯Ò x1,x2,...,xn Î ÒÒ¯©¼ ×­ ¼¯¼× 2¼¯¼ ¯Ò Á¼ »¯¼¯Ò×Îׯå Ò×ׯÒׯÒį ¼ 毩­×Ò w1,w2,...,wn ÎÒÌׯåµìį ×­¼ ×­ »ÁÎ ©¼Îµ Î»Î³Ò ×­× ×­ ŮÇШ}ÌËÐÇ} Á¨ <Üׯ¯µì ŊÁ¼×¯¼Ò ׯµ Á¼Ì× Ŋ毩­× ί׭»×¯ »¼Ō x ¯Ò ¨¯¼ Ò ÒίÌׯÁ¼ ¨ÁÎ ×­ Á¼Ü× Á¨ ©Î¯Üµ×Üεį ÌÁÌܵׯÁ¼į ¼ w x + + w x Á¼Á»¯ ¼ÒÜÒÒ ¯¼ 寵µ©Ò Ò æµµ Ò ¯¼ ¯×¯Ò ¼ ×Áæ¼Ò Á¼ x = 1 1 ··· n n . UkV w + + w Òµ æ­¯­ ¯Ò ÎÎ ¯¼ ¼ì Áܼ×Îì å¼ × ×­ ÌÎÒ¼× ×¯»Į 1 ··· n a­ ׯµ ÒίÌׯÁ¼ Á¨ Á¼×»ÌÁÎÎì ¯¼ÜÒ×ίµ ¼ Á»»Î¯µ ÌÎׯ ÌÁ¯¼×Ò ×Á ­¯©­µì åµÁÌ Ò×ׯÒׯµ ߝࡏߞ ÷Ǖƚ ÚȩɔʕȀŏɟǞɾʿ ŏȘƇ vȒɔȩɟɾŏȘżƚ ȩǀ ɾǕƚ ÒìÒ×»ĮŌ Ł[2]į ÌĮ ĂĊćł ɟǞɾǕȒƚɾǞż ƚŏȘ žÒ ×ίÜ× ×Á VĮĮ E­µ¼Á¯Ò Á¼ ­¯Ò ĂăĆ×­ ¯Î×­ ¼¼¯åÎÒÎì Ł­ æÒ Áμ Á¼ ăĊ 4ܼ ĂĉĊĄłį æ »¼×¯Á¼ a­ žÎ¯×­»×¯ E¼ ŁžĮEĮ ¯¼ Ò­ÁÎ׳ ¯Ò ¨ÎÍܼ׵ì ÜÒ ¼Á× ¨æ Á¨ ×­ Òåε ¨ÁλܵׯÁ¼Ò ¼ Ì̵¯×¯Á¼Ò Á¨ ×­ Á¼µì ¯¼ Ò×ׯÒ×¯Ò ¼ »×­»×¯Òį Ü× µÒÁ ¯¼ ëÌί»¼×µ žÎ¯×­»×¯ E¼ ×­× ÁÜÎ ¯¼ ×­ æÁÎ³Ò Á¨ ¼¯¼× 2¼¯¼ Ò¯¼į Á¼Á»¯Òį ÒÁ¯ÁµÁ©ìį ¼ Á×­Î ¯åÎÒ »¯
    [Show full text]
  • Means, Standard Deviations and Standard Errors
    CHAPTER 4 Means, standard deviations and standard errors 4.1 Introduction Change of units 4.2 Mean, median and mode Coefficient of variation 4.3 Measures of variation 4.4 Calculating the mean and standard Range and interquartile range deviation from a frequency Variance distribution Degrees of freedom 4.5 Sampling variation and Standard deviation standard error Interpretation of the standard Understanding standard deviations deviation and standard errors 4.1 INTRODUCTION A frequency distribution (see Section 3.2) gives a general picture of the distribu- tion of a variable. It is often convenient, however, to summarize a numerical variable still further by giving just two measurements, one indicating the average value and the other the spread of the values. 4.2 MEAN, MEDIAN AND MODE The average value is usually represented by the arithmetic mean, customarily just called the mean. This is simply the sum of the values divided by the number of values. Æx Mean, x n where x denotes the values of the variable, Æ (the Greek capital letter sigma) means `the sum of' and n is the number of observations. The mean is denoted by x (spoken `x bar'). Other measures of the average value are the median and the mode. The median was defined in Section 3.3 as the value that divides the distribution in half. If the observations are arranged in increasing order, the median is the middle observation. (n 1) Median th value of ordered observations 2 34 Chapter 4: Means, standard deviations and standard errors If there is an even number of observations, there is no middle one and the average of the two `middle' ones is taken.
    [Show full text]
  • An Exposition on Means Mabrouck K
    Louisiana State University LSU Digital Commons LSU Master's Theses Graduate School 2004 Which mean do you mean?: an exposition on means Mabrouck K. Faradj Louisiana State University and Agricultural and Mechanical College, [email protected] Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_theses Part of the Applied Mathematics Commons Recommended Citation Faradj, Mabrouck K., "Which mean do you mean?: an exposition on means" (2004). LSU Master's Theses. 1852. https://digitalcommons.lsu.edu/gradschool_theses/1852 This Thesis is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Master's Theses by an authorized graduate school editor of LSU Digital Commons. For more information, please contact [email protected]. WHICH MEAN DO YOU MEAN? AN EXPOSITION ON MEANS A Thesis Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Master of Science in The Department of Mathematics by Mabrouck K. Faradj B.S., L.S.U., 1986 M.P.A., L.S.U., 1997 August, 2004 Acknowledgments This work was motivated by an unpublished paper written by Dr. Madden in 2000. This thesis would not be possible without contributions from many people. To every one who contributed to this project, my deepest gratitude. It is a pleasure to give special thanks to Professor James J. Madden for helping me complete this work. This thesis is dedicated to my wife Marianna for sacrificing so much of her self so that I may realize my dreams.
    [Show full text]
  • The Precision of the Arithmetic Mean, Geometric Mean And
    1 The precision of the arithmetic mean, geometric mean and percentiles for citation data: An experimental simulation modelling approach1 Mike Thelwall, Statistical Cybermetrics Research Group, School of Mathematics and Computer Science, University of Wolverhampton, Wulfruna Street, Wolverhampton, UK. When comparing the citation impact of nations, departments or other groups of researchers within individual fields, three approaches have been proposed: arithmetic means, geometric means, and percentage in the top X%. This article compares the precision of these statistics using 97 trillion experimentally simulated citation counts from 6875 sets of different parameters (although all having the same scale parameter) based upon the discretised lognormal distribution with limits from 1000 repetitions for each parameter set. The results show that the geometric mean is the most precise, closely followed by the percentage of a country’s articles in the top 50% most cited articles for a field, year and document type. Thus the geometric mean citation count is recommended for future citation-based comparisons between nations. The percentage of a country’s articles in the top 1% most cited is a particularly imprecise indicator and is not recommended for international comparisons based on individual fields. Moreover, whereas standard confidence interval formulae for the geometric mean appear to be accurate, confidence interval formulae are less accurate and consistent for percentile indicators. These recommendations assume that the scale parameters of the samples are the same but the choice of indicator is complex and partly conceptual if they are not. Keywords: scientometrics; citation analysis; research evaluation; geometric mean; percentile indicators; MNCS 1. Introduction The European Union and some countries and regions produce periodic reports that compare their scientific performance with the world average or with appropriate comparators (EC, 2007; Elsevier, 2013; NIFU, 2014; NISTEP, 2014; NSF, 2014; Salmi, 2015).
    [Show full text]
  • Characterization of Background Water Quality for Streams and Groundwater
    NATURAL RESOURCES DEFENSE COUNCIL’S & POWDER RIVER BASIN RESOURCE COUNCIL’S PETITION FOR REVIEW EXHIBIT 14 5644 CHARACTERIZATION OF BACKGROUND WATER QUALITY FOR STREAMS AND GROUNDWATER FERNALD ENVIRONMENTAL MANAGEMENT PROJECT FERNALD, OHIO REMEDIAL INVESTIGATION and FEASIBILITY STUDY I- May 1994 . U.S. DEPARTMENT OF ENERGY FERNALD FIELD OFFICE DRAFT’”FINAL 4 .,. ., J I 5644 Background Study May 1994 TABLE OF CONTENTS Eiw? List of Tables iv List of Figures vii List of Acronyms viii 1.0 Introduction - 1-1 1.1 Brief History of the Site 1-1 1.2 Purpose 1-3 1.3 Geologic Setting 1-4 1.4 Hydrologic Setting 1-7 1.4.1 Great Miami River 1-7 1.4.2 Paddys Run 1-10 1.4.3 Great Miami Aquifer 1-11 1.4.4 Glacial Overburden 1-13 1.4.5 Monitoring Wells 1-13 1.5 EPA Guidance on Background Characterization 1-15 1.6 Summary of Revisions Made to the Draft Report (May 1993) 1-16 2.0 Previous Studies 2-1 2.1 Environmental Monitoring Program 2-1 2.2 U.S. Geological Survey Surface Water Monitoring 2-1 2.3 U.S. Geological Survey Groundwater Study 2-3 2.4 IT Corporation Final Interim Report 2-3 2.5 Argonne National Laboratory Environmental Survey 2-3 2.6 Ohio Department of Health 2-3 2.7 Ohio Environmental Protection Agency Study of the Great Miami River 2-6 2.8 Previous RI/FS Background Studies 2-6 2.9 RCRA Groundwater Monitoring 2-7 3.0 Development of the RI/FS Background Data Set 3-1 3.1 Sampling Locations 3-1 3.1.1 Surface Water, 3-1 3.1.2 Groundwater 3-2 3.1.2.1 Identification of Potential Background Monitoring Wells 3-2 3.1.2.2 Screening of Background Locations
    [Show full text]
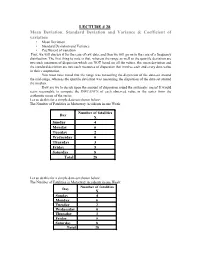
  • LECTURE # 28 Mean Deviation, Standard Deviation and Variance
    LECTURE # 28 Mean Deviation, Standard Deviation and Variance & Coefficient of variation • Mean Deviation • Standard Deviation and Variance • Coefficient of variation First, we will discuss it for the case of raw data, and then we will go on to the case of a frequency distribution. The first thing to note is that, whereas the range as well as the quartile deviation are two such measures of dispersion which are NOT based on all the values, the mean deviation and the standard deviation are two such measures of dispersion that involve each and every data-value in their computation. You must have noted that the range was measuring the dispersion of the data-set around the mid-range, whereas the quartile deviation was measuring the dispersion of the data-set around the median. How are we to decide upon the amount of dispersion round the arithmetic mean? It would seem reasonable to compute the DISTANCE of each observed value in the series from the arithmetic mean of the series. Let us do this for a simple data-set shown below: The Number of Fatalities in Motorway Accidents in one Week: Number of fatalities Day X Sunday 4 Monday 6 Tuesday 2 Wednesday 0 Thursday 3 Friday 5 Saturday 8 Total 28 Let us do this for a simple data-set shown below: The Number of Fatalities in Motorway Accidents in one Week: Number of fatalities Day X Sunday 4 Monday 6 Tuesday 2 Wednesday 0 Thursday 3 Friday 5 Saturday 8 Total 28 The arithmetic mean number of fatalities per day is ∑ X 28 X = = = 4 n 7 In order to determine the distances of the data-values from the mean, we subtract our value of the arithmetic mean from each daily figure, and this gives us the deviations that occur in the third column of the table below: Number of fatalities Day X X − X Sunday 4 0 Monday 6 + 2 Tuesday 2 – 2 Wednesday 0 – 4 Thursday 3 – 1 Friday 5 + 1 Saturday 8 + 4 TOTAL 28 0 The deviations are negative when the daily figure is less than the mean (4 accidents) and positive when the figure is higher than the mean.
    [Show full text]