Players' Average Marginal Contribution in Basketball And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Thunder on the Water
EUSTIS BLANKS LAKE MINNEOLA, SPORTS B1 LEESBURG, FLORIDA Saturday, March 22, 2014 www.dailycommercial.com HEALTH CARE: People find freedom to 50 YEARS: Disney marks start business and still get coverage, C3 ‘small world’ anniversary, A4 TAVARES State will not fine Lake over class-size violations LIVI STANFORD | Staff Writer ducted a self-audit and cor- ed data,” said Cheryl Etters, in February, Superintendent This follows the determi- [email protected] rected its data within the spokeswoman for the FL- Susan Moxley called for an nation that six school prin- The Florida Department appeal window, according DOE, in an email. “They did independent review of all cipals broke the law by inac- of Education will not fine to FLDOE officials. so within the appeal win- schools in the district to de- curately reporting their class Lake County schools for “The district determined, dow. They were never out of termine whether any class- sizes to the state. class-size violations report- based on the audit, that they compliance.” size violations were know- Because the district ed because the district con- needed to submit updat- During a press conference ingly made. SEE SCHOOLS | A2 TAVARES LEESBURG Leesburg weighs county fire merger LIVI STANFORD | Staff Writer [email protected] The city of Leesburg is exploring the op- tion of consolidating its fire and emergency services with Lake County, City Manager Al Minner confirmed on Friday. “There is not enough money to support quality fire services,” he said, explaining the PHOTOS BY BRETT LE BLANC / DAILY COMMERCIAL city spends $285 per capita on fire services Paul Mezyk drives his Jersey Skiff Last Blast during Friday testing for the Spring Thunder Classic Race Boat Regatta on Lake compared with $150 per capita spent by fire Dora in Tavares on Friday. -

Past Match-Ups & Game Notes
Turkish Airlines EuroLeague PAST MATCH-UPS & GAME NOTES REGULAR SEASON - ROUND 17 EUROLEAGUE 2019-20 | REGULAR SEASON | ROUND 17 1 Jan 02, 2020 CET: 19:00 LOCAL TIME: 20:00 | ZALGIRIO ARENA ZALGIRIS KAUNAS MACCABI FOX TEL AVIV 92 ULANOVAS, EDGARAS 12 DIBARTOLOMEO, JOHN Forward | 1.99 | Born: 1992 Guard | 1.83 | Born: 1991 40 GRIGONIS, MARIUS 50 ZOOSMAN, YOVEL Guard | 1.98 | Born: 1994 Guard | 2.00 | Born: 1998 34 LANDALE, JOCK 28 BLACK, TARIK Center | 2.11 | Born: 1995 Center | 2.06 | Born: 1991 32 LEDAY, ZACH 8 AVDIJA, DENI Forward | 2.02 | Born: 1994 Guard | 2.05 | Born: 2001 31 JOKUBAITIS, ROKAS 7 CASSPI, OMRI Guard | 1.93 | Born: 2000 Forward | 2.05 | Born: 1988 23 GEBEN, MARTINAS 1 WILBEKIN, SCOTTIE Center | 2.08 | Born: 1994 Guard | 1.88 | Born: 1993 21 MILAKNIS, ARTURAS 15 COHEN, JAKE Guard | 1.95 | Born: 1986 Forward | 2.10 | Born: 1990 16 LUKOSIUNAS, KAROLIS 14 WOLTERS, NATE Forward | 1.95 | Born: 1997 Guard | 1.93 | Born: 1991 @NateWolters 13 JANKUNAS, PAULIUS 11 DORSEY, TYLER Forward | 2.05 | Born: 1984 Guard | 1.96 | Born: 1996 @P_Jankunas13 12 VENSKUS, ERIKAS 5 HUNTER, OTHELLO Center | 2.05 | Born: 2000 Center | 2.03 | Born: 1986 10 HAYES, NIGEL 2 ACY, QUINCY Forward | 2.03 | Born: 1994 Forward | 2.01 | Born: 1990 0 WALKUP, THOMAS 0 BRYANT, ELIJAH Guard | 1.93 | Born: 1992 Guard | 1.96 | Born: 1995 4 LEKAVICIUS, LUKAS 6 COHEN, SANDY Guard | 1.80 | Born: 1994 Guard | 1.98 | Born: 1995 1 RIVERS, KC 4 CALOIARO, ANGELO Guard | 1.96 | Born: 1987 Forward | 2.03 | Born: 1989 PAST MATCH-UPS & GAME NOTES EUROLEAGUE MEDIA EUROLEAGUE -

2017-18 Media Guide.Pub
1 2 TABLE OF CONTENTS LAKERS STAFF LAKERS PLAYOFF RECORDS Team Directory 6 Year-by-Year Playoff Results 96 President/CEO Joey Buss 7 Head-to-Head vs. Opponents 96 General Manager Nick Mazzella 7 Career Playoff Leaders 97 Head Coach Coby Karl 8 All-Time Single-Game Highs 98 Assistant Coach Brian Walsh 8 All-Time Highs / Lows 99 Assistant Coach Isaiah Fox 8 Lakers Individual Records 100 Assistant Coach Dane Johnson 9 Opponent All-Time Highs / Lows 101 Assistant Coach Sean Nolen 9 All-Time Playoff Scores 102 Player Development Coach Metta World Peace 9 Video Coordinator Anthony Beaumont 9 THE OPPONENTS Athletic Trainer Heather Mau 10 G League Map 104 Strength & Conditioning Coach Misha Cavaye 10 Agua Caliente Clippers of Ontario 105 Basketball Operations Coordinator Nick Lagios 10 Director of Scouting Jesse Buss 10 Austin Spurs 106 Canton Charge 107 Delaware 87ers 108 HE LAYERS Erie BayHawks 109 T P Fort Wayne Mad Ants 110 Individual Bios 12-23 Grand Rapids Drive 111 Greensboro Swarm 112 THE G LEAGUE Iowa Wolves 113 G League Directory 25 Lakeland Magic 114 NBA G League Key Dates 26 Long Island Nets 115 2016-17 Final Standings 27 Maine Red Claws 116 2016-17 Team Statistics 28-29 Memphis Hustle 117 2016-17 NBA G League Leaders 30 Northern Arizona Suns 118 2016-17 Highs / Lows 30 Oklahoma City Blue 119 Champions By Year 31 Raptors 905 120 NBA G League Award Winners 31 Reno Bighorns 121 2017 NBA G League Draft 32 Rio Grande Valley Vipers 122 NBA G League Single-Game Bests 33 Salt Lake City Stars 123 Santa Cruz Warriors 124 2016-17 YEAR IN REVIEW -

Past Match-Ups & Game Notes
Turkish Airlines EuroLeague PAST MATCH-UPS & GAME NOTES REGULAR SEASON - ROUND 2 EUROLEAGUE 2019-20 | REGULAR SEASON | ROUND 2 1 Oct 10, 2019 CET: 19:00 LOCAL TIME: 19:00 | STARK ARENA CRVENA ZVEZDA MTS BELGRADE FENERBAHCE BEKO ISTANBUL 50 OJO, MICHAEL 12 KALINIC, NIKOLA Center | 2.16 | Born: 1993 Forward | 2.02 | Born: 1991 @nikola_kalinic 32 JOVANOVIC, NIKOLA 35 MUHAMMED, ALI Center | 2.11 | Born: 1994 Guard | 1.78 | Born: 1983 @BobbyDixon20 28 SIMANIC, BORISA 24 VESELY, JAN Forward | 2.09 | Born: 1998 Center | 2.13 | Born: 1990 @JanVesely24 13 DOBRIC, OGNJEN 21 WILLIAMS, DERRICK Guard | 2.00 | Born: 1994 Forward | 2.03 | Born: 1991 12 BARON, BILLY 19 DE COLO, NANDO Guard | 1.88 | Born: 1990 Guard | 1.96 | Born: 1987 @billy_baron @nandodecolo 10 LAZIC, BRANKO 77 LAUVERGNE, JOFFREY Guard | 1.95 | Born: 1989 Center | 2.11 | Born: 1991 9 NENADIC, NEMANJA 70 DATOME, LUIGI Forward | 1.97 | Born: 1994 Forward | 2.03 | Born: 1987 @GigiDatome 7 DAVIDOVAC, DEJAN 44 DUVERIOGLU, AHMET Forward | 2.02 | Born: 1995 Center | 2.09 | Born: 1993 5 PERPEROGLOU, STRATOS 16 SLOUKAS, KOSTAS Forward | 2.03 | Born: 1984 Guard | 1.90 | Born: 1990 4 BROWN, LORENZO 10 MAHMUTOGLU, MELIH Guard | 1.96 | Born: 1990 Guard | 1.91 | Born: 1990 22 JENKINS, CHARLES 9 WESTERMANN, LEO Guard | 1.91 | Born: 1989 Guard | 1.98 | Born: 1992 @thejenkinsguy22 @lwestermann 15 GIST, JAMES 3 TIRPANCI, ERGI Forward | 2.04 | Born: 1986 Guard | 2.00 | Born: 2000 3 COVIC, FILIP 13 BIBEROVIC, TARIK Guard | 1.80 | Born: 1989 Forward | 2.01 | Born: 2001 1 BROWN, DERRICK 91 STIMAC, VLADIMIR -

Past Match-Ups & Game Notes
Turkish Airlines EuroLeague PAST MATCH-UPS & GAME NOTES REGULAR SEASON - ROUND 1 EUROLEAGUE 2019-20 | REGULAR SEASON | ROUND 1 1 Oct 03, 2019 CET: 19:00 LOCAL TIME: 20:00 | ARENA MYTISHCHI KHIMKI MOSCOW REGION MACCABI FOX TEL AVIV 11 JEREBKO, JONAS 12 DIBARTOLOMEO, JOHN Center | 2.08 | Born: 1987 Guard | 1.83 | Born: 1991 10 DESIATNIKOV, ANDREI 50 ZOOSMAN, YOVEL Center | 2.20 | Born: 1994 Guard | 2.00 | Born: 1998 45 BERTANS, DAIRIS 28 BLACK, TARIK Guard | 1.92 | Born: 1989 Center | 2.06 | Born: 1991 31 VALIEV, EVGENY 8 AVDIJA, DENI Forward | 2.05 | Born: 1990 Guard | 2.05 | Born: 2001 25 MOZGOV, TIMOFEY 7 CASSPI, OMRI Center | 2.16 | Born: 1986 Forward | 2.05 | Born: 1988 24 JOVIC, STEFAN 1 WILBEKIN, SCOTTIE Guard | 1.98 | Born: 1990 Guard | 1.88 | Born: 1993 13 GILL, ANTHONY 15 COHEN, JAKE Forward | 2.04 | Born: 1992 Forward | 2.10 | Born: 1990 9 VIALTSEV, EGOR 14 WOLTERS, NATE Forward | 1.93 | Born: 1985 Guard | 1.93 | Born: 1991 @NateWolters 8 ZAYTSEV, VYACHESLAV 11 DORSEY, TYLER Guard | 1.90 | Born: 1989 Guard | 1.96 | Born: 1996 7 KARASEV, SERGEY 5 HUNTER, OTHELLO Forward | 2.01 | Born: 1993 Center | 2.03 | Born: 1986 5 BOOKER, DEVIN 2 ACY, QUINCY Center | 2.05 | Born: 1991 Forward | 2.01 | Born: 1990 12 MONIA, SERGEY 0 BRYANT, ELIJAH Forward | 2.02 | Born: 1983 Guard | 1.96 | Born: 1995 6 TIMMA, JANIS 6 COHEN, SANDY Forward | 2.01 | Born: 1992 Guard | 1.98 | Born: 1995 3 KRAMER, CHRIS Guard | 1.91 | Born: 1988 PAST MATCH-UPS & GAME NOTES EUROLEAGUE MEDIA EUROLEAGUE 2019-20 | REGULAR SEASON | ROUND 1 2 Oct 03, 2019 CET: 19:00 LOCAL -

Past Match-Ups & Game Notes
Turkish Airlines EuroLeague PAST MATCH-UPS & GAME NOTES REGULAR SEASON - ROUND 28 EUROLEAGUE 2019-20 | REGULAR SEASON | ROUND 28 1 Mar 06, 2020 CET: 19:00 LOCAL TIME: 19:00 | STARK ARENA CRVENA ZVEZDA MTS BELGRADE MACCABI FOX TEL AVIV 50 OJO, MICHAEL 12 DIBARTOLOMEO, JOHN Center | 2.16 | Born: 1993 Guard | 1.83 | Born: 1991 32 JOVANOVIC, NIKOLA 50 ZOOSMAN, YOVEL Center | 2.11 | Born: 1994 Guard | 2.00 | Born: 1998 28 SIMANIC, BORISA 28 BLACK, TARIK Forward | 2.09 | Born: 1998 Center | 2.06 | Born: 1991 13 DOBRIC, OGNJEN 8 AVDIJA, DENI Guard | 2.00 | Born: 1994 Guard | 2.05 | Born: 2001 12 BARON, BILLY 7 CASSPI, OMRI Guard | 1.88 | Born: 1990 Forward | 2.05 | Born: 1988 @billy_baron 10 LAZIC, BRANKO 1 WILBEKIN, SCOTTIE Guard | 1.95 | Born: 1989 Guard | 1.88 | Born: 1993 7 DAVIDOVAC, DEJAN 15 COHEN, JAKE Forward | 2.02 | Born: 1995 Forward | 2.10 | Born: 1990 5 PERPEROGLOU, STRATOS 14 WOLTERS, NATE Forward | 2.03 | Born: 1984 Guard | 1.93 | Born: 1991 @NateWolters 4 BROWN, LORENZO 11 DORSEY, TYLER Guard | 1.96 | Born: 1990 Guard | 1.96 | Born: 1996 22 JENKINS, CHARLES 5 HUNTER, OTHELLO Guard | 1.91 | Born: 1989 Center | 2.03 | Born: 1986 @thejenkinsguy22 15 GIST, JAMES 2 ACY, QUINCY Forward | 2.04 | Born: 1986 Forward | 2.01 | Born: 1990 21 JAGODIC-KURIDZA, MARKO 0 BRYANT, ELIJAH Forward | 2.05 | Born: 1987 Guard | 1.96 | Born: 1995 91 STIMAC, VLADIMIR 6 COHEN, SANDY Center | 2.10 | Born: 1987 Guard | 1.98 | Born: 1995 00 PUNTER, KEVIN 4 CALOIARO, ANGELO Guard | 1.93 | Born: 1993 Forward | 2.03 | Born: 1989 PAST MATCH-UPS & GAME NOTES EUROLEAGUE -
NCAA Bowl Eligibility Policies
TABLE OF CONTENTS 2019-20 Bowl Schedule ..................................................................................................................2-3 The Bowl Experience .......................................................................................................................4-5 The Football Bowl Association What is the FBA? ...............................................................................................................................6-7 Bowl Games: Where Everybody Wins .........................................................................8-9 The Regular Season Wins ...........................................................................................10-11 Communities Win .........................................................................................................12-13 The Fans Win ...................................................................................................................14-15 Institutions Win ..............................................................................................................16-17 Most Importantly: Student-Athletes Win .............................................................18-19 FBA Executive Director Wright Waters .......................................................................................20 FBA Executive Committee ..............................................................................................................21 NCAA Bowl Eligibility Policies .......................................................................................................22 -
So Long at the Fair
First victory: Every claims PGA Tour win at Bay Hill /B1 MONDAY TODAY CITRUS COUNTY & next morning HIGH 72 Mostly cloudy, LOW 50% chance of rain showers. 56 PAGE A4 www.chronicleonline.com MARCH 24, 2014 Florida’s Best Community Newspaper Serving Florida’s Best Community 50¢ VOL. 119 ISSUE 229 INSIDE STATE NEWS: Flood rates Cook tackles biggest problem fast The Legislature moves MIKE WRIGHT But the soft-spoken Cook week he and Duke reached Commissioners were im- forward on a plan to didn’t interrupt as Greene, or agreement on not only the pressed that Cook was able entice private insurance Staff writer the attorneys, or the Duke ex- 2012 and 2013 contested as- to find settlement just two companies./Page A3 INVERNESS — Les Cook ecutives, or their lawyers, de- sessments, but also the 2014 months on the job. CITRUS COUNTY FAIR: always had a plan. bated the company’s 2012 assessment as well. “What you see is his ability Every time he joined his and 2013 taxable assessments The agreement ends costly to find a conclusion to this Fair coupon boss, Property Appraiser that the two sides were litigation and gives local gov- that is very beneficial to our Find the coupon for a Geoff Greene, in negotiations nowhere near to solving. ernments breathing room in community,” Commissioner discounted midway ride with Duke Energy over the So it came as a relief to Cit- knowing the largest taxpayer Joe Meek said. “Regardless Les Cook armband./Page A6 power company’s lawsuits rus County commissioners in the county has its taxable of the final figures .. -

The Seekers Undergraduate Researchers Set out on Life-Altering Quests
No. 2, 2014 I $5 The Seekers Undergraduate researchers set out on life-altering quests I W ARRIOR A RT I ST I O PERA STAR Contents | March 2014 20 26 30 20 26 30 COVER STORY The Good Fight Strength of Character Inquiring Minds An Iraq war veteran struggling Mezzo-soprano Phyllis with post-traumatic stress Pancella shares with students Undergraduate Research nds his footing with the help her secrets for success: passion Awards free students to of a KU Wounded Warrior and preparation. experience scholarship’s joy of Scholarship. victory— and agony of defeat. By Jennifer Jackson Sanner By Chris Lazzarino By Chris Lazzarino Cover image of Holly Laerty by Kelsey Kimberlin Established in 1902 as e Graduate Magazine Volume 112, No. 2, 2014 ISSUE 2, 2014 | 1 Lift the Chorus Near missus her undergraduate and master’s degrees at KU, and for Your many years was a professor opinion counts Editor’s Note: An online and administrator at KU. Please email us a note invitation for alumni to share their at [email protected] KU love stories for Valentine’s She also had been warned about the Green Hall steps. She to tell us what you think of Day attracted this letter from a your alumni magazine. longtime Kansas Alumni reader was a resident of Douthart and stalwart Jayhawk. Scholarship Hall during the Vietnam anti-war disturbances at KU. A number of we law less I nd this bias in Kansas M I did students volunteered to stay in Alumni oensive. not meet my sweethearts the old law library one night Surely that boy and girl at KU. -
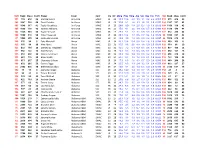
Team Conf 25 Michael Lyons Air Force MWC JR 23 40 Todd
HnR Rank Class ConR Player Team Conf Cla GP Mn/g Pt/g Rb/g A/g S/g B/g T/g TS% HnI Rank Class ConR 111 772 238 25 Michael Lyons Air Force MWC JR 23 33.1 15.6 4.0 1.5 1.1 0.2 2.4 0.551 113 673 212 23 105 1047 316 40 Todd Fletcher Air Force MWC JR 29 30.9 8.1 2.6 3.3 1.6 0.1 1.9 0.571 104 1107 337 42 105 1048 317 41 Taylor Broekhuis Air Force MWC JR 29 29.8 9.0 4.8 2.0 0.7 1.0 1.9 0.572 104 1108 338 43 105 1068 136 42 Kamryn Williams Air Force MWC FR 29 15.0 4.1 2.6 1.4 0.6 0.7 1.0 0.490 103 1130 146 44 104 1125 363 44 Taylor Stewart Air Force MWC SR 15 27.1 8.1 2.9 3.1 0.8 0.3 1.5 0.521 107 912 298 32 100 1300 378 50 Mike Fitzgerald Air Force MWC JR 29 29.1 10.4 3.8 0.6 0.7 0.4 1.6 0.632 99 1352 391 51 97 1480 215 56 Justin Hammonds Air Force MWC FR 24 13.9 4.5 1.9 0.5 0.5 0.2 0.8 0.597 96 1519 218 57 129 276 94 5 Zeke Marshall Akron MAC JR 34 26.1 10.4 5.4 0.8 0.4 2.8 1.6 0.584 128 299 106 6 125 350 94 10 Alex Abreu Akron MAC SO 31 30.5 9.6 2.6 4.8 1.8 0.0 2.5 0.611 126 339 86 10 122 432 114 14 Demetrius Treadwell Akron MAC SO 32 16.5 7.2 5.1 0.9 0.5 0.6 1.3 0.497 122 437 109 14 117 558 142 15 Nick Harney Akron MAC SO 29 15.3 8.3 2.9 0.6 0.6 0.1 1.6 0.574 117 550 141 15 115 618 202 16 Nikola Cvetinovic Akron MAC SR 34 25.9 9.9 5.4 1.8 0.8 0.2 1.9 0.531 114 636 210 16 113 683 175 20 Brian Walsh Akron MAC SO 34 24.7 8.3 3.9 1.2 0.9 0.1 1.0 0.597 112 723 184 22 110 813 257 25 Chauncey Gilliam Akron MAC JR 34 17.1 6.5 1.6 0.8 0.7 0.0 0.6 0.580 109 840 264 26 109 852 265 26 Quincy Diggs Akron MAC JR 34 25.5 8.5 3.1 2.4 1.2 0.1 2.4 0.550 108 -

Communications
DEC. 21, 2019 | VILLANOVA | GAME NOTES KANSAS COMMUNICATIONS 9-1 0-0 #1 / #1 8-2 0-0 #18 / #14 WILDCATS OVERALL BIG 12 RANKING (AP/COACHES) OVERALL BIG EAST RANKING (AP/COACHES) -VS- Bill Self 482-107 (.818) Jay Wright 456-177 (.720) JAYHAWKS HEAD COACH RECORD AT KU, 17TH SEASON HEAD COACH RECORD AT NOVA, 19TH SEASON GAME SCHEDULE (H: 6-0; A: 0-0; N: 3-1) KANSAS AT VILLANOVA SERIES AT A GLANCE KU OPP BIG EAST/BIG 12 BATTLE OVERALL TIED, 4-4 Date Rnk Rnk Opponent TV Time/Result Philadelphia, Pa. • Wells Fargo Center (20,056) in Philadelphia Villanova leads, 1-0 NOVEMBER (6-1) 11 Last Meeting W, 74-71 @ KU, 12/15/2018 5 3/3 4/4 vs. Duke! ESPN L, 66-68 Saturday, December 21, 2019 • 12 p.m. (ET)/11 a.m. (CT) 8 3/3 -/- UNCG ESPNU W, 74-62 15 5/3 -/- MONMOUTH B12 NOW W, 112-57 FOX JAYHAWK RADIO 19 4/5 -/- EAST TENNESSEE ST.~ B12 NOW W, 75-63 NETWORK Play-by-Play: Gus Johnson Radio: IMG Jayhawk Radio Network 25 4/5 -/- vs. Chaminade# ESPNU W, 93-63 Analyst: Jim Jackson Webcast: KUAthletics.com/Radio 26 4/5 -/- vs. BYU# ESPN W, 71-56 Reporter: Andy Katz Play-by-Play: Brian Hanni ‹‹ POINTS 27 4/5 rv/rv vs. Dayton# ESPN W, 90-84 (ot) Producer: Matt Gangl Analyst: Greg Gurley 84.6 PER GAME 80.4 DECEMBER (3-0) Producer/Engineer: Steve Kincaid 7 2/3 20/21 COLORADO ESPN2 W, 72-58 TIP-OFF 52.6 ‹‹ FG% 48.5 10 2/3 -/- MILWAUKEE B12 NOW W, 95-68 • No. -

PROBABLE STARTING LINEUPS Louisville Cardinals Vs. Cincinnati
Louisville Basketball Quick Facts Location Louisville, Ky. 40292 Founded / Enrollment 1798 / 22,000 Nine NCAA Final Fours 1980, 1986 NCAA Champions 38 NCAA Tournament Appearances Nickname/Colors Cardinals / Red and Black Conference BIG EAST Sports Information University of Louisville Louisville, KY 40292 www.GoCards.com Home Court KFC Yum! Center (22,000) Phone: (502) 852-6581 Fax: (502) 852-7401 email: [email protected] President Dr. James Ramsey Vice President for Athletics Tom Jurich Louisville Cardinals vs. Cincinnati Bearcats Head Coach Rick Pitino (UMass '74) U of L Record 299-111 (12th yr.) PROBABLE STARTING LINEUPS Overall Record 653-239 (28th yr.) Louisville (24-5, 12-4) Ht. Wt. Yr. PPG RPG Hometown Asst. Coaches Wyking Jones, Kevin Keatts, Kareem Richardson F 20 Wayne BLACKSHEAR 6-5 230 So. 8.4 3.4 Chicago, Ill. Dir. of Basketball Operations Andre McGee F 21 Chane BEHANAN 6-6 250 So. 10.7 7.4 Cincinnati, Ohio All-Time Record 1,686-869 (99th yr.) C 10 Gorgui DIENG 6-11 245 Jr. 9.9 10.1 Kebemer, Senegal All-Time NCAA Tournament Record 64-40 G 2 Russ SMITH 6-1 165 Jr. 18.4 3.8 Brooklyn, N.Y. (38 Appearances, Nine Final Fours, G 3 Peyton SIVA 6-0 185 Sr. 9.8 2.2 Seattle, Wash. Two NCAA Championships - 1980, 1986) Important Phone Numbers CIncinnati (20-9, 8-8) Ht Wt. Yr. PPG RPG Hometown Athletics Office (502) 852-5732 F 2 Titus RUBLES 6-7 207 Jr. 6.2 5.8 Dallas, Texas Basketball Office (502) 852-6651 C 13 Cheikh MBODJ 6-10 236 Sr.