DOCSLIB.ORG

Key Questions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Key Questions 2/28/14 Things you should know when you leave… Key Questions ECE 340 • Why do carriers diffuse? Lecture 16 and 17: Diffusion • What happens when we add an electric of Carriers field to our carrier gradient? • How can I visualize this from a band Class Outline: diagram? • What is the general effect of including recombination in our considerations? •Diffusion Processes • What is the relationship between •Diffusion and Drift of Carriers diffusion and mobility? M.J. Gilbert ECE 340 – Lecture 16 and 17 Diffusion Processes Diffusion Processes What happens when we have a concentration discontinuity?? Let’s shine light on a localized part of a semiconductor… Now let’s monitor the system… Consider a situation where we spray perfume in the corner of a room… •Assume thermal motion . • If there is no convection or motion of air, then the scent spreads by diffusion. •Carriers move by interacting with the lattice or impurities. • This is due to the random motion of particles. •Thermal motion causes particles to jump to an •Particles move randomly until they collide with an air molecule which changes adjacent compartment. it’s direction. •After the mean-free time (τ ), half of • c If the motion is truly random, then a particle sitting in some volume has equal particles will leave and half will remain a probabilities of moving into or out of the volume at some time interval. certain volume. 1024 T = 0 512 512 512 256 256 384 384 Shouldn’t the same thing happen T1 = 0 in a semiconductor if we have 1024 t = 3τ t = 0 t =τ c t = 2τ c 128 128 c 256 spatial gradients of carriers? T2 = 0 • 320 256 Process continues until uniform concentration. 192 •We must have a concentration gradient for T3 = 0 t = 6τ c diffusion to start. M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 1 2/28/14 Diffusion Processes Diffusion Processes How do we describe this physical process?? So we have a flux of particles… We want to calculate the rate at which electrons diffuse in a simple one- The rate of electron flow in the +x direction dimensional example. Consider an arbitrary electron distribution… (per unit area): λ φ = n − n •Divide the distribution into n ( 1 2 ) 2τ c incremental distances of the mean-free path (λ). Since the mean-free path is a small differential •Evaluate n(x) in the center length, we can write the electron difference as: of the segments. φn = In the limit of small Δx, or small •Electrons on the left of x n(x)− n(x + Δx) 0 n − n = λ mean-free path between collisions… have a 50% chance of 1 2 Δx moving left or right in a 2 time, τc. λ n(x)− n(x + Δx) λ •Same is true for electrons φn (x) = lim Δx→0 τ c Δx λ λ to the right of x0. λ2 dn(x) = − Net # of electrons moving from left 1 1 τ dx Diffusion coefficient (n1λA)− (n2λA) c 2 to right in one τc. 2 2 (cm /sec) λ λ M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 Diffusion Processes Diffusion and Drift of Carriers But we already expected this… How do we handle a concentration gradient and an electric field? Define the carrier flux for E electrons and holes: e- The total current must be the sum of the electron and hole currents resulting dn x J (x) = J n + J p ( ) from the drift and diffusion processes φn (x)= −Dn dx h+ n(x) dn x ( ) Electrons dp(x) J n (x)= qµnn(x)E(x)+ qDn φ p (x)= −Dp dx dx p(x) dp(x) And the corresponding current densities associated with diffusion… J n (x)= qµ p p(x)E(x)− qD p Holes x dx n dn(x) J diff = qDn Drift Diffusion dx Where are the particles and currents flowing? φn (diff) φ (drift) p dp(x) φp (diff and drift) n J = −qD diff n dx Jp (diff and drift) Jp (diff) Jn (drift) Carriers move together, currents Dashed Arrows = Particle Flow ! !Solid Arrows = Resulting Currents! opposite directions. !! M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 2 2/28/14 Diffusion and Drift of Carriers Diffusion and Drift of Carriers A few extra observations… Can we relate the diffusion coefficient to the mobility? φn (diff) φ (drift) We can by using what we know about drift, diffusion, and band bending… φp (diff and drift) n Jp (diff and drift) Jp (diff) Jn (drift) •In equilibrium, no current flows. •Any fluctuation that would begin a diffusion current also Dashed Arrows = Particle Flow ! !Solid Arrows = Resulting Currents! sets up an electric field which redistributes the carriers !! by drift. dn x •Diffusion currents are in opposite directions. ( ) J n (x)= qµnn(x)E(x)+ qDn = 0 •Drift currents are in the same direction. dx •Currents depend on: Dn 1 dn(x) •Relative electron and hole concentrations. Solve for the electric field E(x): E(x) = •Magnitude and directions of electric field. µn n(x) dx •Carrier gradients. (EF −Ei ) k T b DN kbT dn x It’s equilibrium, so we know n(x): n(x) = nie ( ) •Diffusion currents can be large even = J n (x)= qµnn(x)E(x)+ qDn E E q dx if the carriers are in the minority by ( F − i ) q µ N dn(x) ni k T dEi q b (qnE)µn − (qnE) DN = 0 several orders of magnitude. = − e = − nE k T dp x dx kbT dx kbT b ( ) •Not true for drift currents. DP kbT J n (x)= qµ p p(x)E(x)− qD p = dx Assuming E is non-zero µP q M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 Diffusion and Drift of Carriers Diffusion and Drift of Carriers These relations are called the Einstein relations… Recall the previous example… Ec D k T Assume that: N b = Ei •It is silicon maintained at 300 K. µ N q Ef •E – E = E /4 at ± L and E – E = DP kbT f i g f i Ev = Eg/4 at x = 0. µP q •Choose the Fermi level as the reference energy. •The balance of drift and diffusion currents creates a built-in x electric field to accompany any gradient in the bands. -L 0 L E = −∇V E •Gradients in the bands can occur at equilibrium when: 1 V V = − (Ec − Eref ) 1 dE 1 dE 1 dE q = c = v = i q dx q dx q dx E V • the band gap varies. = −∇ • 1 dEc 1 dEv 1 dEi x alloy concentration varies. = = = x • q dx q dx q dx dopant concentrations vary. -L 0 L -L 0 L M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 3 2/28/14 Diffusion and Drift of Carriers Diffusion and Drift of Carriers Question: Is it in equilibrium? Ec What are the electron and hole Ec current densities at ± L/2: Energy Ei Ei Ef Ef Ef It is in equilibrium, so JP and JN = Ev 0. Ev Material 1 Material 2 DOS – N1(E) DOS – N2(E) FD – f1(E) FD – f2(E) x Roughly sketch n and p inside the x •Assume two materials in sample: intimate contact. -L 0 L -L 0 L •In thermal equilibrium. p • Rate1-2 N E f E • N E 1− f E No current. 1( ) 1( ) 2 ( )[ 2 ( )] n •No net energy transfer. i •Carriers moving from 2 to 1 Rate2-1 N2 (E)f2 (E)• N1(E)[1− f1(E)] must be balanced by carriers n moving from 1 to 2. Rate1-2 = Rate2-1 x dEF = 0 YES -L 0 L Therefore… f1(E) = f2(E) Ef1 = Ef2 dx M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 Diffusion and Drift of Carriers Diffusion and Recombination What are the electron diffusion Ec So what does this mean? current at ± L/2? If so, in what direction? Ei There is a diffusion current at Ef both L/2 and –L/2. Ev dn n At –L/2: > 0 J dx diff dn n x At L/2: < 0 J diff dx What are the electron drift current -L 0 L Consider this semiconductor: at ± L/2? If so, in what direction? drift •The hole current density leaving the differential area may be Jn = −qn vdn = qnµnE n larger or smaller than the current density that enters the area. At –L/2: J drift •This is a result of recombination and generation. n •Net increase in hole concentration per unit time, dp/dt, is At L/2: J drift difference between hole flux per unit volume entering and DP kbT What is the diffusion = Use Einstein 11.9 cm2/sec leaving, minus the recombination rate. coefficient? relation µP q M.J. Gilbert ECE 340 – Lecture 16 and 17 M.J. Gilbert ECE 340 – Lecture 16 and 17 4 2/28/14 Diffusion and Recombination Diffusion and Recombination How can we explain this? Are there any simplifications? The net increase in hole concentration per unit If the current is carried mainly by diffusion (small drift) we can replace the time is the difference between the hole flux currents in the continuity equation… entering and leaving minus the recombination rate… n ∂n dn(x) J diff = qDN J x = qµ n x E x + qD ∂x n ( ) n ( ) ( ) n ∂p 1 J P (x)− J P (x + Δx) Δp dx = − p ∂p ∂t x x x q Δx τ p dp x → +Δ J diff = −qDP ( ) J n (x)= qµ p p(x)E(x)− qD p ∂x dx Rate of hole Increase in hole Recombination We put this back into the continuity equations… buildup.
Load more

Recommended publications
  • LECTURE 18 – Pn DIODE Devices the Pn Junction the First Device We
    LECTURE 18 – pn DIODE Devices The pn Junction The first device we will look at is the pn diode. Junction Formation Thought experiment - consider what happens if n and p type semiconductor samples are placed together. electrons + - n + - p + - holes uncompensated donors uncompensated acceptors (stuck in lattice) metallurgical (stuck in lattice) junction Due to diffusion we have two effects: • electrons pour out of n-type material, leaving behind uncompensated donors (+ ions) • holes pour out of p-type material, leaving behind uncompensated acceptors (- ions) These electrons and holes then recombine, producing a region depleted of free carriers, leaving only fixed charges (ionized donors and acceptors). Lecture 18: pn Diode September, 2000 1 The diffusion process can not continue indefinitely as the space charge creates an electric field that opposes the diffusion of majority carriers (electrons in n-type and holes in p-type), though such diffusion is not prevented altogether. W depletion region n + - p + - ε built in electric field The electric field will sweep minority carriers (holes in n- type and electrons in p-type) across the junction so that there is a drift current of electrons from the p- to the n-type side and of holes from the n- to the p-type side which is in the opposite direction to the diffusion current. The junction field builds up until these two current flows are equal and equilibrium is achieved (no net current flow). It is a basic result of thermodynamics that in equilibrium the Fermi energy must be the same throughout the system. The induced electric field establishes a contact potential (φ) between the two regions and the energy bands of the p-type side are displaced relative to those of the n-type side.
    [Show full text]
  • Lecture 3 Electron and Hole Transport in Semiconductors Review
    Lecture 3 Electron and Hole Transport in Semiconductors In this lecture you will learn: • How electrons and holes move in semiconductors • Thermal motion of electrons and holes • Electric current via drift • Electric current via diffusion • Semiconductor resistors ECE 315 – Spring 2005 – Farhan Rana – Cornell University Review: Electrons and Holes in Semiconductors holes + electrons + + As Donor A Silicon crystal lattice + impurity + As atoms + ● There are two types of mobile charges in semiconductors: electrons and holes In an intrinsic (or undoped) semiconductor electron density equals hole density ● Semiconductors can be doped in two ways: N-doping: to increase the electron density P-doping: to increase the hole density ECE 315 – Spring 2005 – Farhan Rana – Cornell University 1 Thermal Motion of Electrons and Holes In thermal equilibrium carriers (i.e. electrons or holes) are not standing still but are moving around in the crystal lattice because of their thermal energy The root-mean-square velocity of electrons can be found by equating their kinetic energy to the thermal energy: 1 1 m v 2 KT 2 n th 2 KT vth mn In pure Silicon at room temperature: 7 vth ~ 10 cm s Brownian Motion ECE 315 – Spring 2005 – Farhan Rana – Cornell University Thermal Motion of Electrons and Holes In thermal equilibrium carriers (i.e. electrons or holes) are not standing still but are moving around in the crystal lattice and undergoing collisions with: • vibrating Silicon atoms • with other electrons and holes • with dopant atoms (donors or acceptors) and
    [Show full text]
  • Theoretical Analysis on Transient Photon-Generated Voltage in Polymer Based Organic Devices
    Electronic Supplementary Material (ESI) for Physical Chemistry Chemical Physics This journal is © The Owner Societies 2012 Supporting Information (SI) Theoretical Analysis on transient photon-generated voltage in polymer based organic devices. 5 To further confirm the conclusion in the manuscript, a theoretical model, simultaneously taking into account the possible excitons and carrier processes in the active polymer layer after photo excitation and the interaction of different polar species formed in different phases has been developed. The interphasic and 10 intraphasic interactions have to be considered in the studies of Device No.1, 2 and 3. For Device No.2 and Device No.3, since one pristine polymer is used for these devices, intraphasic interaction will dominate the processes. However, as polymer blend is used in Device 1, both interphasic and intraphasic interactions will exist. The details are discussed as belows. 15 We present a time-dependent device model, describing the dynamical processes of both excitons induced by light illumination and charge carriers created from the exciton dissociation in pristine polymer layer and blend layer. Then we calculate the transient photovoltage (TPV) in single-layer organic photovoltaic cells. With the 20 model, the theoretical TPV has been determined and analyzed with the experimental results for further verifying the conclusion of this work. Considering (1) the laser pulse transmits into the polymer layer through the ITO side; (2) the absorption length of polymer layer is much less than the thickness of polymer 25 layer in our devices, for example, for Device No. 3, the absorption length is around 100 nm and thickness of P3HT layer is around 240nm and (3) the exciton lifetime is ultra-short with a value around 500 ps, excitons will have very little population near interface of polymer layer/Al which will thus be ignored in the model.
    [Show full text]
  • “Complementi Di Fisica” Lectures 25-26
    “Complementi di Fisica” Lectures 25-26 Livio Lanceri Università di Trieste Trieste, 14/15-12-2015 in these lectures • Introduction – Non or quasi-equilibrium: “excess” carriers injection – Processes for “generation” and “recombination” of carriers – Continuity equations for carriers • Continuity equations: three important special cases – Steady-state injection from one side • “diffusion length” Lp – Minority carriers recombination at the surface • diffusion length and “surface recombination velocity” Slr – The Haynes-Shockley experiment • Evidence for simultaneous diffusion, drift and recombination • Are we describing the behaviour of minority carriers alone? What about majority carriers? – Why are “minorities” important? Some examples… – Built-in electric field (Gauss!) and “ambipolar” transport equations 14/15-12-2015 L.Lanceri - Complementi di Fisica - Lectures 25-26 2 In these lectures • Reference textbooks – D.A. Neamen, Semiconductor Physics and Devices, McGraw- Hill, 3rd ed., 2003, p.189-230 (“6 Nonequilibrium excess carriers in semiconductors”) – R.Pierret, Advanced Semiconductor Fundamental, Prentice Hall, 2nd ed., p.134-174 (“5 Recombination-Generation Processes”) – J.Nelson, The Physics of Solar Cells, Imperial College Press, p. 79-117 (Ch.4, “Generation and Recombination”) 14/15-12-2015 L.Lanceri - Complementi di Fisica - Lectures 25-26 3 Injection of “excess” carriers Non-equilibrium! (in some cases: quasi-equilibrium) Carrier injection - introduction • “carrier injection” = process of introducing “excess” 2 carriers in a
    [Show full text]
  • Lecture 12: Photodiode Detectors
    Lecture 12: Photodiode detectors Background concepts p-n photodiodes Photoconductive/photovoltaic modes p-i-n photodiodes Responsivity and bandwidth Noise in photodetectors References: This lecture partially follows the materials from Photonic Devices, Jia-Ming Liu, Chapter 14. Also from Fundamentals of Photonics, 2nd ed., Saleh & Teich, Chapters 18. 1 Electron-hole photogeneration Most modern photodetectors operate on the basis of the internal photoelectric effect – the photoexcited electrons and holes remain within the material, increasing the electrical conductivity of the material Electron-hole photogeneration in a semiconductor • absorbed photons generate free electron- h hole pairs h Eg • Transport of the free electrons and holes upon an electric field results in a current 2 Absorption coefficient Bandgaps for some semiconductor photodiode materials at 300 K Bandgap (eV) at 300 K Indirect Direct Si 1.14 4.10 Ge 0.67 0.81 - 1.43 kink GaAs InAs - 0.35 InP - 1.35 GaSb - 0.73 - 0.75 In0.53Ga0.47As - 1.15 In0.14Ga0.86As - 1.15 GaAs0.88Sb0.12 3 Absorption coefficient E.g. absorption coefficient = 103 cm-1 Means an 1/e optical power absorption length of 1/ = 10-3 cm = 10 m Likewise, = 104 cm-1 => 1/e optical power absorption length of 1 m. = 105 cm-1 => 1/e optical power absorption length of 100 nm. = 106 cm-1 => 1/e optical power absorption length of 10 nm. 4 Indirect absorption Silicon and germanium absorb light by both indirect and direct optical transitions. Indirect absorption requires the assistance of a phonon so that momentum and energy are conserved.
    [Show full text]
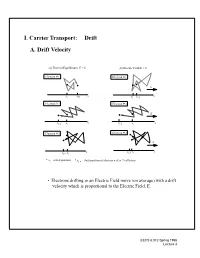
  • B. Diffusion Current Density- Holes ¥ Current Density = (Charge) X (# Carriers Per Second Per Area)
    I. Carrier Transport: Drift B.A. DiffusionDrift Velocity Current Density- Holes • Current density = (charge) x (# carriers per second per area): 1 1 (a) Thermal Equilibrium, E =- -0 px()–λAλ–--(b)px Electric()+ FieldλA E λ> 0 diff 2 2 J = q --------------------------------------------------------------- Electron # 1 p Electronτ # 1 Ac E • If we assume the mean free path is much smaller than the dimensions x x x x of our device,i f,then1 we can consider λ = dx xandi xf, 1use Electrona Taylor# 2 expansion on p(x - λ) andElectron p(x #+ 2 λ): E diff dp x λ2x τ x • J xf,2 =xi –qD , where Dp = f, 2/ c is xthei diffusion coefficent p pdx Electron # 3 Electron # 3 • Holes diffuse down the concentration gradient and carryE positive charge. x xf,3 xi x xf,3 xi * xi = initial position * xf, n = final position of electron n after 7 collisions • Electrons drifting in an Electric Field move (on average) with a drift velocity which is proportional to the Electric Field, E. EECS 6.012 Spring 1998 Lecture 3 Drift Velocity (Cont.) Velocity in Direction of E Field t qE vat==± ------- t m qτ c vave =– ---------- E 2mn • mn is an effective mass to take into account quantum mechanics µ 2 • Lump it into a quantity we call mobility n (units:cm /V-s) µ vd = - nE EECS 6.012 Spring 1998 Lecture 3 B. Electron and Hole Mobility • mobilities vary with doping concentration-- plot is for 300K 1400 1200 electrons 1000 Vs) / 2 800 600 mobility (cm holes 400 200 0 1013 1014 1015 1016 1017 1018 1019 1020 + −3 Nd Na total dopant concentration (cm ) • “typical values” for bulk silicon -- 300 K µ 2 n = 1000 cm /(Vs) µ 2 p = 400 cm /(Vs) EECS 6.012 Spring 1998 Lecture 3 C.
    [Show full text]
  • Effect of Drift and Diffusion Processes in the Change of the Current Direction in a Fet Transistor
    EFFECT OF DRIFT AND DIFFUSION PROCESSES IN THE CHANGE OF THE CURRENT DIRECTION IN A FET TRANSISTOR By OSCAR VICENTE HUERTA GONZALEZ A Dissertation submitted to the program in Electronics, in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE WITH SPECIALTY IN ELECTRONICS At the National Institute por Astrophysics, Optics and Electronics (INAOE) Tonantzintla, Puebla February, 2014 Supervised by: DR. EDMUNDO A. GUTIERREZ DOMINGUEZ INAOE ©INAOE 2014 All rights reserved The author hereby grants to INAOE permission to reproduce and to distribute copies of this thesis document in whole or in part. DEDICATION There are several people which I would like to dedicate this work. First of all, to my parents, Margarita González Pantoja and Vicente Huerta Escudero for the love and support they have given me. They are my role models because of the hard work and sacrifices they have made so that my brothers and me could set high goals and achieve them. To my brothers Edgard de Jesus and Jairo Arturo, we have shared so many things, and helped each other on our short lives. I would also like to thank Lizbeth Robles, one special person in my life, thanks for continuously supporting and encouraging me to give my best. And thanks to every member of my family and friends for their support. They have contributed to who I am now. ACKNOWLEDGEMENTS I would like to thank the National Institute for Astrophysics, Optics and Electronics (INAOE) for all the facilities that contributed to my successful graduate studies. To Consejo Nacional de Ciencia y Tecnologia (CONACYT) for the economic support.
    [Show full text]
  • Lecture 3 Semiconductor Physics (II) Carrier Transport
    Lecture 3 Semiconductor Physics (II) Carrier Transport Outline • Thermal Motion •Carrier Drift •Carrier Diffusion Reading Assignment: Howe and Sodini; Chapter 2, Sect. 2.4-2.6 6.012 Spring 2007 Lecture 3 1 1. Thermal Motion In thermal equilibrium, carriers are not sitting still: • Undergo collisions with vibrating Si atoms (Brownian motion) • Electrostatically interact with each other and with ionized (charged) dopants Characteristic time constant of thermal motion: ⇒ mean free time between collisions τc ≡ collison time [s] In between collisions, carriers acquire high velocity: −1 vth ≡ thermal velocity [cms ] …. but get nowhere! 6.012 Spring 2007 Lecture 3 2 Characteristic length of thermal motion: λ≡mean free path [cm] λ = vthτc Put numbers for Si at room temperature: −13 τc ≈ 10 s 7 −1 vth ≈ 10 cms ⇒ λ ≈ 0.01 µm For reference, state-of-the-art production MOSFET: Lg ≈ 0.1 µm ⇒ Carriers undergo many collisions as they travel through devices 6.012 Spring 2007 Lecture 3 3 2. Carrier Drift Apply electric field to semiconductor: E ≡ electric field [V cm-1] ⇒ net force on carrier F = ±qE E Between collisions, carriers accelerate in the direction of the electrostatic field: qE v(t) = a •t =± t mn,p 6.012 Spring 2007 Lecture 3 4 But there is (on the average) a collision every τc and the velocity is randomized: net velocity τc in direction of field time The average net velocity in direction of the field: qE qτc v = vd =± τ c =± E 2mn,p 2mn,p This is called drift velocity [cm s-1] Define: qτ c 2 −1 −1 µn,p = ≡ mobility[cm V s ] 2mn,p Then, for electrons: vdn = −µnE and for holes: vdp = µpE 6.012 Spring 2007 Lecture 3 5 Mobility - is a measure of ease of carrier drift • If τc ↑, longer time between collisions ⇒ µ ↑ • If m ↓, “lighter” particle ⇒ µ ↑ At room temperature, mobility in Si depends on doping: 1400 1200 electrons 1000 Vs) / 2 800 600 mobility (cm holes 400 200 0 1013 1014 1015 1016 1017 1018 1019 1020 + −3 Nd Na total dopant concentration (cm ) • For low doping level, µ is limited by collisions with lattice.
    [Show full text]
  • 1. Diffusion: the Flow of Charge Due to Density Gradients
    1. Diffusion: the flow of charge due to density gradients. a. Diffusion Current The diffusion currents are expressed in terms of the electron or hole diffusion coefficient Dn or Dp, as shown below: dn dn Jn,diff = (q)Dn = qDn dx dx dn dp J = (+q)D = qD p,diff p dx p dx b. Einstein Relation: kT D = μ n q n kT D = μ p q p 2. Total Current: J = Jdiff + Jdrift EXAMPLE1: We have a piece of uniformly doped silicon with a acceptor concentration of Na=2E16cm-3. By shedding light on one end (x=0) of the semiconductor, we creat an electron concentration of n(x)=1E13*exp(-x/2um). Calculate the electron diffusion current as a function of x. SOLUTION1: 2 Na = 2E16 μn = 1050cm / Vs kT D = μ = 0.026 1050 = 27.3cm2 / s n q n dn d x /2104 Jn,diff = qDn = 1.6 1019 27.3 1013 e () dx dx () = 0.22e x /2μm A / cm2 3. Integrated Passives a. Resistors -Diffusion Resistor: ion implantation/diffusion 100ohm/sq(unsilicided),10ohm/sq(silicided) -Poly Film Resistor: deposit a thin film of heavily doped poly-Si 10-100ohm/sq(unsilicided),1ohm/sq(silicided) b. Capacitors -IC MIM Capacitor: by forming a Metal plate-Insulator(thin oxide)-Metal plate structure. -Parallel Plate Capacitor: A C = d -Nonlinear capacitor: Q-V curve is not a straight line Small signal capacitance: differential capacitance df (V) Q = Q + q f (Vs) + v 0 dV s V =Vs df (V) C dV V =Vs 4. PN Junction a.
    [Show full text]
  • Chapter 5: the Pn Junction
    Chapter 5: The pn Junction Nonequilibrium excess carriers in semiconductors Carrier generation and recombination Mathematical analysis of excess carriers Ambipolar transport The pn junction Basic structure of the pn junction Zero applied bias Reverse applied bias Non-uniformly doped junctions The pn junction diode Ideal current/voltage relationship Small-signal model of the pn junction Generation/recombination currents Junction breakdown PHYS5320 Chapter Five (II) 1 Ideal Current/Voltage Relationship kT N N V ln a d bi 2 e ni The built-in potential Vbi maintains equilibrium between the carrier distributions on both sides of the junction. Consider n2 eV the electrons in the n-region first. i bi exp Na Nd kT PHYS5320 Chapter Five (II) 2 Ideal Current/Voltage Relationship Let nn0 and np0 denote the thermal equilibrium concentrations of the electrons in the n-region (majority) and in the p-region (minority), respectively. If we assume complete ionization, we have 2 ni nn0 Nd np0 Na 2 ni np0 eVbi exp Na Nd nn0 kT The equation relates the minority carrier electron concentration on the p- eV side to the majority carrier electron bi concentration on the n-side of the np0 nn0 exp kT junction. PHYS5320 Chapter Five (II) 3 Ideal Current/Voltage Relationship If a positive voltage is applied to the p-region with respect to the n-region, the potential barrier is reduced. This bias condition is known as the forward bias. Almost all of this bias voltage is across the junction region. The forward bias reduces the potential barrier and disturb the thermal equilibrium.
    [Show full text]
  • ENEE 313, Spr '09 Midterm II Solution
    ENEE 313, Spr ’09 Midterm II Solution PART I—DRIFT AND DIFFUSION, 30 pts 1. We have a silicon sample with non-uniform doping. The sample is 200 µm long: In the figure, L = 200 µm= 0.02 cm. At the x = 0 edge, the sample is doped at an acceptor density of 17 3 16 3 NA(0) = 10 1/cm . At the x = L edge, the sample is doped at NA = 5 × 10 1/cm . In between, the doping density varies linearly, as shown in the figure (y-axis not to scale). (a) (2 pts.) What type is the material? The material is p-type. (b) (10 pts.) Sketch the equilibrium hole concentration p0(x). Approximately calculate and roughly sketch the equilibrium electron concentration n0(x). (Hint: The doping 17 18 concentration can be written in terms of x as NA(x) = 10 − 2.5 × 10 x, where x is given in units of cm.) p0(x) ≈ NA(x) 2 20 ni 2.1 × 10 n0(x) = = 17 18 p0 10 − 2.5 × 10 x 3 ⇒ n0(0) = 2.1 × 10 ; n0(L) = 4200 (See next page for the sketch.) (c) (8 pts.) Assume this sample is at equilibrium. Mark the directions of diffusion for the majority and for the minority carriers. Mark the direction of the electric field Ebi(x) which must be built-in to oppose this diffusion current at equilibrium. The majority carriers are the holes, and they will diffuse towards +ˆx, as the h+ concentration decreases in that direction. The minority carriers are the electrons, and they will diffuse towards −xˆ, as the e− concentration decreases in that direction.
    [Show full text]
  • Drift in Semiconductors
    Lawrence Berkeley National Laboratory Recent Work Title SEMICONDUCTOR VARIABLE DELAY ELEMENTS. Permalink https://escholarship.org/uc/item/8bs3w7h5 Author Tuyl, Rory Lynn. Van Publication Date 1968-12-01 eScholarship.org Powered by the California Digital Library University of California UCRL-18668 RE~EIVED lAW:mJCE RACIATlo;~ LAa0RATORV APR '7 l~b~ LIBRARY AND DOCUMENTS SECTION SEMICONDUCTOR VARIABLE DELAY ELEMENTS Rory Lynn Van Tuyl (M. S. Thesis) December 1968 -,I TWO-WEEK LOAN COPY ,I I This is a Librar~ Circulating Copy I which may be borrowed for two weeks. j ,}, for a personal retention copy. call 1 , . , i Tech. Info. Di~-ision. Ex-t~ 5545'-'-------~~- i II _-./_" ~l~ ___ ~_-""--l-='-=--_--.-.J""·--~---""'i-~ -~ ~J ~ ~ LAWRENCE RADIATION LABORATOR~ ~ UNIVERSITY of CALIFORNIA BERKELEyH ~ DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof or the Regents of the University of California.
    [Show full text]