DOCSLIB.ORG

New Arithmetic Algorithms for Hereditarily Binary Natural Numbers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
New Arithmetic Algorithms for Hereditarily Binary Natural Numbers 1 New Arithmetic Algorithms for Hereditarily Binary Natural Numbers Paul Tarau Deptartment of Computer Science and Engineering University of North Texas [email protected] Abstract—Hereditarily binary numbers are a tree-based num- paper and discusses future work. The Appendix wraps our ber representation derived from a bijection between natural arithmetic operations as instances of Haskell’s number and numbers and iterated applications of two simple functions order classes and provides the function definitions from [1] corresponding to bijective base 2 numbers. This paper describes several new arithmetic algorithms on hereditarily binary num- referenced in this paper. bers that, while within constant factors from their traditional We have adopted a literate programming style, i.e., the counterparts for their average case behavior, make tractable code contained in the paper forms a Haskell module, avail- important computations that are impossible with traditional able at http://www.cse.unt.edu/∼tarau/research/2014/hbinx.hs. number representations. It imports code described in detail in the paper [1], from file Keywords-hereditary numbering systems, compressed number ∼ representations, arithmetic computations with giant numbers, http://www.cse.unt.edu/ tarau/research/2014/hbin.hs. A Scala compact representation of large prime numbers package implementing the same tree-based computations is available from http://code.google.com/p/giant-numbers/. We hope that this will encourage the reader to experiment inter- I. INTRODUCTION actively and validate the technical correctness of our claims. This paper is a sequel to [1]1 where we have introduced a tree based number representation, called hereditarily binary II. HEREDITARILY BINARY NUMBERS numbers. We will summarize, following [1], the basic concepts behind In [1] we present specialized algorithms for basic arithmetic hereditarily binary numbers. Through the paper, we denote N operations (addition, subtraction, comparison, double, half, the set of natural numbers and N+ the set of strictly positive exponent of 2 and bitsize), that favor numbers with relatively natural numbers. few blocks of contiguous 0 and 1 bijective base-2 digits, for which dramatic complexity reductions result even when A. Bijective base-2 numbers operating on very large, “towers-of-exponents” numbers. Natural numbers can be seen as represented by iterated This paper covers several new arithmetic operations on applications of the functions o(x) = 2x+1 and i(x) = 2x+2 hereditarily binary numbers and some specialized arithmetic corresponding to the so called bijective base-2 representation algorithms that are used in number theory and cryptography, (defined for an arbitrary base in [3] pp. 90-92 as “m-adic” like modular operations and Miller-Rabin and Lucas-Lehmer numbers). Each n 2 can be seen as a unique composition primality tests. N of these functions. We can make this precise as follows: In addition, we perform a performance evaluation confirm- Definition 1: We call bijective base-2 representation of n 2 ing our theoretical complexity estimates of [1] and illustrate the unique sequence of applications of functions o and i to compact representations of some record-holder large prime N 0 that evaluates to n. numbers, while emphasizing that hereditarily binary numbers With this representation, one obtains ; 1 = o(0); 2 = i(0); 3 = replace bitsize with a measure of structural complexity as the o(o(0)); 4 = i(o(0)); 5 = o(i(0)) etc. Clearly: key parameter deciding tractability of arithmetic operations. The paper is organized as follows. Section II overviews i(x) = o(x) + 1 (1) basic definitions for hereditarily binary numbers and sum- marizes some of their properties, following [1]. Section III B. Efficient arithmetic with iterated functions on and in describes new arithmetic algorithms for hereditarily binary Several arithmetic identities are proven in [1] and used to numbers. Section IV compares the performance of several express efficient “one block of on or in operations at a time” algorithms operating on hereditarily binary numbers with algorithms for various arithmetic operations. Among them, their conventional counterparts. Section V illustrates compact we recall the following two, showing the connection of our tree-representations of some record-holder number-theoretical iterated function applications with “left shift/multiplication by entities like Mersenne, Fermat, Proth and Woodall primes. a power of 2” operations. Section VI discusses related work. Section VII concludes the 1An extended draft version of [1] is available at the arxiv repository [2]. on(k) = 2n(k + 1) − 1 (2) 2 in(k) = 2n(k + 2) − 2 (3) III. ARITHMETIC OPERATIONS WORKING ONE ok OR ik BLOCK AT A TIME In particular In [1] we provide algorithms for the basic arithmetic op- on(0) = 2n − 1 (4) erations of addition (add) subtraction (sub), exponent of 2 (exp2), multiplication by a power of 2, division by a power of 2 (leftshiftBy, rightshiftBy) arithmetic compari- in(0) = 2n+1 − 2 (5) son (cmp) and computation of the size of the equivalent binary representation of a number, bitsize. We will describe in this section algorithms for several other arithmetic operations, C. Hereditarily binary numbers as a data type optimized for working one block of ok or ik applications at First we define a data type for our tree represented natural a time. numbers, that we call hereditarily binary numbers to empha- size that binary rather than unary encoding is recursively used General multiplication in their representation. Like in the case of add and sub operations in [1] we can Definition 2: The data type T of the set of hereditarily binary numbers is defined in [1] by the Haskell declaration: derive a multiplication algorithm based on several arithmetic data T = E | V T [T] | W T [T] identities involving exponents of 2 and iterated applications of deriving (Eq,Read,Show) the functions o and i. corresponding to the recursive data type equation T = 1 + T × Proposition 1: The following holds: T∗ + T × T∗. on(a)om(b) = on+m(ab + a + b) − on(a) − om(b) (7) The intuition behind the type T is the following: • The term E (empty leaf) corresponds to zero Proof: By (2), we can expand and then reduce: n m n m • the term V x xs counts the number x+1 of o applica- o (a)o (b) = (2 (a + 1) − 1)(2 (b + 1) − 1) = n+m n m tions followed by an alternation of similar counts of i 2 (a + 1)(b + 1) − (2 (a + 1) + 2 (b + 1)) + 1 = n+m n m and o applications xs 2 (a+1)(b+1)−1−(2 (a+1)−1+2 (b+1)−1+2)+2 = n+m n m • the term W x xs counts the number x+1 of i applica- o (ab + a + b + 1) − (o (a) + o (b)) − 2 + 2 = n+m n m tions followed by an alternation of similar counts of o o (ab + a + b) − o (a) − o (b) and i applications xs Proposition 2: n m n+m n+1 m+1 In [1] the bijection between N and T is provided by the i (a)i (b) = i (ab+2(a+b+1))+2−i (a)−i (b) function n : T ! N and its inverse t : N ! T. (8) Definition 3: The function n : T ! N shown in equation Proof: By (3), we can expand and then reduce: (6) defines the unique natural number associated to a term of in(a)im(b) = (2n(a + 2) − 2)(2m(b + 2) − 2) = type T. 2n+m(a + 2)(b + 2) − (2n+1(a + 2) − 2 + 2m+1(b + 2) − 2) = n+m n+1 m+1 This bijection ensures that hereditarily binary numbers provide 2 (a + 2)(b + 2) − i (a) − i (b) = n+m n+1 m+1 a canonical representation of natural numbers and the equality 2 (a + 2)(b + 2) − 2 − (i (a) + i (b)) + 2 = n+m n+1 m+1 relation on type T can be derived by structural induction. 2 (ab + 2a + 2b + 2 + 2) − 2 − (i (a) + i (b)) + 2 = n+m n+1 m+1 The following examples show the workings of the bijection i (ab + 2a + 2b + 2) − (i (a) + i (b)) + 2 = n+m n+1 m+1 n and illustrate that “structural complexity”, defined in [1] i (ab + 2(a + b + 1)) + 2 − i (a) − i (b) as the size of the tree representation without the root, is The corresponding Haskell code starts with the obvious base bounded by the bitsize of a number and favors numbers in cases: the neighborhood of towers of exponents of 2. mul _ E = E 16 22 − 1 ! V (V (V (V (V E[])[])[])[])[] mul E _ = E 20+1−1+1 22 −1+1−1+1 ! 22 −1+1 − 1 When both terms represent odd numbers we apply the identity 20 ! W E [E,E,E] (7): ! (((20+1 − 1 + 2)20+1 − 2 + 1)20+1 − 1 + 2)20+1 − 2 mul x y j o_ x && o_ y = r2 where (n,a) = osplit x In [1] basic arithmetic operations are introduced with com- (m,b) = osplit y plexity parameterized by the size of the tree representation of p1 = add (mul a b) (add a b) their operands rather than their bitsize. p2 = otimes (add (s n) (s m)) p1 r1 = sub p2 x After defining constant average time successor and prede- r2 = sub r1 y cessor functions s and s’, constant average time definitions of o and i are given in [1], as well as for the corresponding Note that the function osplit defined in [1] is used to inverse operations o’ and i’, that can be seen as “un- separate the first block of o applications. The next two cases applying” a single instance of o or i, and “recognizers” e_ are reduced to the previous one by using the identity i = s◦o.
Load more

Recommended publications
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • Radix-8 Design Alternatives of Fast Two Operands Interleaved
    International Journal of Advanced Network, Monitoring and Controls Volume 04, No.02, 2019 Radix-8 Design Alternatives of Fast Two Operands Interleaved Multiplication with Enhanced Architecture With FPGA implementation & synthesize of 64-bit Wallace Tree CSA based Radix-8 Booth Multiplier Mohammad M. Asad Qasem Abu Al-Haija King Faisal University, Department of Electrical Department of Computer Information and Systems Engineering, Ahsa 31982, Saudi Arabia Engineering e-mail: [email protected] Tennessee State University, Nashville, USA e-mail: [email protected] Ibrahim Marouf King Faisal University, Department of Electrical Engineering, Ahsa 31982, Saudi Arabia e-mail: [email protected] Abstract—In this paper, we proposed different comparable researches to propose different solutions to ensure the reconfigurable hardware implementations for the radix-8 fast safe access and store of private and sensitive data by two operands multiplier coprocessor using Karatsuba method employing different cryptographic algorithms and Booth recording method by employing carry save (CSA) and kogge stone adders (KSA) on Wallace tree organization. especially the public key algorithms [1] which proved The proposed designs utilized robust security resistance against most of the attacks family with target chip device along and security halls. Public key cryptography is with simulation package. Also, the proposed significantly based on the use of number theory and designs were synthesized and benchmarked in terms of the digital arithmetic algorithms. maximum operational frequency, the total path delay, the total design area and the total thermal power dissipation. The Indeed, wide range of public key cryptographic experimental results revealed that the best multiplication systems were developed and embedded using hardware architecture was belonging to Wallace Tree CSA based Radix- modules due to its better performance and security.
    [Show full text]
  • Power Towers and the Tetration of Numbers
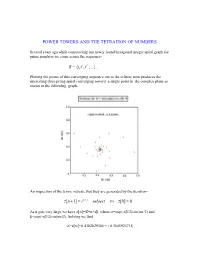
    POWER TOWERS AND THE TETRATION OF NUMBERS Several years ago while constructing our newly found hexagonal integer spiral graph for prime numbers we came across the sequence- i S {i,i i ,i i ,...}, Plotting the points of this converging sequence out to the infinite term produces the interesting three prong spiral converging toward a single point in the complex plane as shown in the following graph- An inspection of the terms indicate that they are generated by the iteration- z[n 1] i z[n] subject to z[0] 0 As n gets very large we have z[]=Z=+i, where =exp(-/2)cos(/2) and =exp(-/2)sin(/2). Solving we find – Z=z[]=0.4382829366 + i 0.3605924718 It is the purpose of the present article to generalize the above result to any complex number z=a+ib by looking at the general iterative form- z[n+1]=(a+ib)z[n] subject to z[0]=1 Here N=a+ib with a and b being real numbers which are not necessarily integers. Such an iteration represents essentially a tetration of the number N. That is, its value up through the nth iteration, produces the power tower- Z Z n Z Z Z with n-1 zs in the exponents Thus- 22 4 2 22 216 65536 Note that the evaluation of the powers is from the top down and so is not equivalent to the bottom up operation 44=256. Also it is clear that the sequence {1 2,2 2,3 2,4 2,...}diverges very rapidly unlike the earlier case {1i,2 i,3i,4i,...} which clearly converges.
    [Show full text]
  • ON PRIME CHAINS 3 Can Be Found in Many Elementary Number Theory Texts, for Example [8]
    ON PRIME CHAINS DOUGLAS S. STONES Abstract. Let b be an odd integer such that b ≡ ±1 (mod 8) and let q be a prime with primitive root 2 such that q does not divide b. We show q−2 that if (pk)k=0 is a sequence of odd primes such that pk = 2pk−1 + b for all 1 ≤ k ≤ q − 2, then either (a) q divides p0 + b, (b) p0 = q or (c) p1 = q. λ−1 For integers a,b with a ≥ 1, a sequence of primes (pk)k=0 such that pk = apk−1+b for all 1 ≤ k ≤ λ − 1 is called a prime chain of length λ based on the pair (a,b). This follows the terminology of Lehmer [7]. The value of pk is given by k k (a − 1) (1) p = a p0 + b k (a − 1) for all 0 ≤ k ≤ λ − 1. For prime chains based on the pair (2, +1), Cunningham [2, p. 241] listed three prime chains of length 6 and identified some congruences satisfied by the primes within prime chains of length at least 4. Prime chains based on the pair (2, +1) are now called Cunningham chains of the first kind, which we will call C+1 chains, for short. Prime chains based on the pair (2, −1) are called Cunningham chains of the second kind, which we will call C−1 chains. We begin with the following theorem which has ramifications on the maximum length of a prime chain; it is a simple corollary of Fermat’s Little Theorem.
    [Show full text]
  • Attributes of Infinity
    International Journal of Applied Physics and Mathematics Attributes of Infinity Kiamran Radjabli* Utilicast, La Jolla, California, USA. * Corresponding author. Email: [email protected] Manuscript submitted May 15, 2016; accepted October 14, 2016. doi: 10.17706/ijapm.2017.7.1.42-48 Abstract: The concept of infinity is analyzed with an objective to establish different infinity levels. It is proposed to distinguish layers of infinity using the diverging functions and series, which transform finite numbers to infinite domain. Hyper-operations of iterated exponentiation establish major orders of infinity. It is proposed to characterize the infinity by three attributes: order, class, and analytic value. In the first order of infinity, the infinity class is assessed based on the “analytic convergence” of the Riemann zeta function. Arithmetic operations in infinity are introduced and the results of the operations are associated with the infinity attributes. Key words: Infinity, class, order, surreal numbers, divergence, zeta function, hyperpower function, tetration, pentation. 1. Introduction Traditionally, the abstract concept of infinity has been used to generically designate any extremely large result that cannot be measured or determined. However, modern mathematics attempts to introduce new concepts to address the properties of infinite numbers and operations with infinities. The system of hyperreal numbers [1], [2] is one of the approaches to define infinite and infinitesimal quantities. The hyperreals (a.k.a. nonstandard reals) *R, are an extension of the real numbers R that contains numbers greater than anything of the form 1 + 1 + … + 1, which is infinite number, and its reciprocal is infinitesimal. Also, the set theory expands the concept of infinity with introduction of various orders of infinity using ordinal numbers.
    [Show full text]
  • Arxiv:Math/0412262V2 [Math.NT] 8 Aug 2012 Etrgae Tgte Ihm)O Atnscnetr and Conjecture fie ‘Artin’S Number on of Cojoc Me) Domains’
    ARTIN’S PRIMITIVE ROOT CONJECTURE - a survey - PIETER MOREE (with contributions by A.C. Cojocaru, W. Gajda and H. Graves) To the memory of John L. Selfridge (1927-2010) Abstract. One of the first concepts one meets in elementary number theory is that of the multiplicative order. We give a survey of the lit- erature on this topic emphasizing the Artin primitive root conjecture (1927). The first part of the survey is intended for a rather general audience and rather colloquial, whereas the second part is intended for number theorists and ends with several open problems. The contribu- tions in the survey on ‘elliptic Artin’ are due to Alina Cojocaru. Woj- ciec Gajda wrote a section on ‘Artin for K-theory of number fields’, and Hester Graves (together with me) on ‘Artin’s conjecture and Euclidean domains’. Contents 1. Introduction 2 2. Naive heuristic approach 5 3. Algebraic number theory 5 3.1. Analytic algebraic number theory 6 4. Artin’s heuristic approach 8 5. Modified heuristic approach (`ala Artin) 9 6. Hooley’s work 10 6.1. Unconditional results 12 7. Probabilistic model 13 8. The indicator function 17 arXiv:math/0412262v2 [math.NT] 8 Aug 2012 8.1. The indicator function and probabilistic models 17 8.2. The indicator function in the function field setting 18 9. Some variations of Artin’s problem 20 9.1. Elliptic Artin (by A.C. Cojocaru) 20 9.2. Even order 22 9.3. Order in a prescribed arithmetic progression 24 9.4. Divisors of second order recurrences 25 9.5. Lenstra’s work 29 9.6.
    [Show full text]
  • CM55: Special Prime-Field Elliptic Curves Almost Optimizing Den Boer's
    CM55: special prime-field elliptic curves almost optimizing den Boer's reduction between Diffie–Hellman and discrete logs Daniel R. L. Brown∗ February 24, 2015 Abstract Using the Pohlig{Hellman algorithm, den Boer reduced the discrete logarithm prob- lem to the Diffie–Hellman problem in groups of an order whose prime factors were each one plus a smooth number. This report reviews some related general conjectural lower bounds on the Diffie–Hellman problem in elliptic curve groups that relax the smoothness condition into a more commonly true condition. This report focuses on some elliptic curve parameters defined over a prime field size of size 9 + 55 × 2288, whose special form may provide some efficiency advantages over random fields of similar sizes. The curve has a point of Proth prime order 1 + 55 × 2286, which helps to nearly optimize the den Boer reduction. This curve is constructed using the CM method. It has cofactor 4, trace 6, and fundamental discriminant −55. This report also tries to consolidate the variety of ways of deciding between elliptic curves (or other algorithms) given the efficiency and security of each. Contents 1 Introduction3 2 Previous Work and Motivation4 2.1 den Boer's Reduction between DHP and DLP . .4 2.2 Complex Multiplication Method of Generating Elliptic Curves . .4 2.3 Earlier Publication of the CM55 Parameters . .4 3 Provable Security: Reducing DLP to DHP5 3.1 A Special Case of den Boer's Algorithm . .5 3.2 More Costly Reductions with Fewer Oracle Calls . .7 3.3 Relaxing the Smoothness Requirements . 11 4 Resisting Other Attacks on CM55 (if Trusted) 13 4.1 Resistance to the MOV Attack .
    [Show full text]
  • Primality Testing for Beginners
    STUDENT MATHEMATICAL LIBRARY Volume 70 Primality Testing for Beginners Lasse Rempe-Gillen Rebecca Waldecker http://dx.doi.org/10.1090/stml/070 Primality Testing for Beginners STUDENT MATHEMATICAL LIBRARY Volume 70 Primality Testing for Beginners Lasse Rempe-Gillen Rebecca Waldecker American Mathematical Society Providence, Rhode Island Editorial Board Satyan L. Devadoss John Stillwell Gerald B. Folland (Chair) Serge Tabachnikov The cover illustration is a variant of the Sieve of Eratosthenes (Sec- tion 1.5), showing the integers from 1 to 2704 colored by the number of their prime factors, including repeats. The illustration was created us- ing MATLAB. The back cover shows a phase plot of the Riemann zeta function (see Appendix A), which appears courtesy of Elias Wegert (www.visual.wegert.com). 2010 Mathematics Subject Classification. Primary 11-01, 11-02, 11Axx, 11Y11, 11Y16. For additional information and updates on this book, visit www.ams.org/bookpages/stml-70 Library of Congress Cataloging-in-Publication Data Rempe-Gillen, Lasse, 1978– author. [Primzahltests f¨ur Einsteiger. English] Primality testing for beginners / Lasse Rempe-Gillen, Rebecca Waldecker. pages cm. — (Student mathematical library ; volume 70) Translation of: Primzahltests f¨ur Einsteiger : Zahlentheorie - Algorithmik - Kryptographie. Includes bibliographical references and index. ISBN 978-0-8218-9883-3 (alk. paper) 1. Number theory. I. Waldecker, Rebecca, 1979– author. II. Title. QA241.R45813 2014 512.72—dc23 2013032423 Copying and reprinting. Individual readers of this publication, and nonprofit libraries acting for them, are permitted to make fair use of the material, such as to copy a chapter for use in teaching or research. Permission is granted to quote brief passages from this publication in reviews, provided the customary acknowledgment of the source is given.
    [Show full text]
  • The Notion Of" Unimaginable Numbers" in Computational Number Theory
    Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers.
    [Show full text]
  • Hyperoperations and Nopt Structures
    Hyperoperations and Nopt Structures Alister Wilson Abstract (Beta version) The concept of formal power towers by analogy to formal power series is introduced. Bracketing patterns for combining hyperoperations are pictured. Nopt structures are introduced by reference to Nept structures. Briefly speaking, Nept structures are a notation that help picturing the seed(m)-Ackermann number sequence by reference to exponential function and multitudinous nestings thereof. A systematic structure is observed and described. Keywords: Large numbers, formal power towers, Nopt structures. 1 Contents i Acknowledgements 3 ii List of Figures and Tables 3 I Introduction 4 II Philosophical Considerations 5 III Bracketing patterns and hyperoperations 8 3.1 Some Examples 8 3.2 Top-down versus bottom-up 9 3.3 Bracketing patterns and binary operations 10 3.4 Bracketing patterns with exponentiation and tetration 12 3.5 Bracketing and 4 consecutive hyperoperations 15 3.6 A quick look at the start of the Grzegorczyk hierarchy 17 3.7 Reconsidering top-down and bottom-up 18 IV Nopt Structures 20 4.1 Introduction to Nept and Nopt structures 20 4.2 Defining Nopts from Nepts 21 4.3 Seed Values: “n” and “theta ) n” 24 4.4 A method for generating Nopt structures 25 4.5 Magnitude inequalities inside Nopt structures 32 V Applying Nopt Structures 33 5.1 The gi-sequence and g-subscript towers 33 5.2 Nopt structures and Conway chained arrows 35 VI Glossary 39 VII Further Reading and Weblinks 42 2 i Acknowledgements I’d like to express my gratitude to Wikipedia for supplying an enormous range of high quality mathematics articles.
    [Show full text]
  • Goldbach's Conjecture
    U.U.D.M. Project Report 2020:37 Goldbach’s Conjecture Johan Härdig Examensarbete i matematik, 15 hp Handledare: Veronica Crispin Quinonez Examinator: Martin Herschend Augusti 2020 Department of Mathematics Uppsala University Goldbach's Conjecture Johan H¨ardig Contents 1 Introduction 3 1.1 Definition of the Conjectures . 3 2 Prime Numbers and their Distribution 4 2.1 Early Results . 4 2.2 Prime Number Theorem . 6 3 Heuristic and Probabilistic Justification 8 3.1 Method Presented by Gaze & Gaze . 8 3.1.1 Sieve Method by Gaze & Gaze . 9 3.1.2 Example . 10 3.2 Prime Number Theorem for Arithmetic Progressions . 11 3.3 Distribution of Primes Across Prime Residue Classes . 14 3.4 Heuristic Justification by Gaze & Gaze . 15 3.4.1 Conclusion . 16 3.5 Goldbach's Comet . 17 4 The Ternary Goldbach's Conjecture 18 4.1 Historical Overview . 18 4.2 Approach . 19 4.3 Theorems and Methods in the Proof . 20 4.3.1 Hardy-Littlewood Circle Method . 20 4.3.2 Vinogradov's Theorem . 22 4.3.3 The Large Sieve . 24 4.3.4 L-functions . 24 4.3.5 Computational Methods . 26 4.4 The Proof . 29 1 CONTENTS 2 Abstract The following text will provide a historical perspective as well as investigate different approaches to the unsolved mathematical problem Goldbach's conjecture stated by Christian Goldbach in the year 1742. First off, there will be an overview of the early history of prime num- bers, and then a brief description of the Prime Number Theorem. Subsequently, an example of a heuristic and probabilistic method of justifying the binary Goldbach's conjecture, proposed by Gaze and Gaze, will be discussed.
    [Show full text]
  • Primegrid's Mega Prime Search
    PrimeGrid’s Mega Prime Search On 23 October 2012, PrimeGrid’s Proth Prime Search project found the Mega Prime: 9*23497442 +1 The prime is 1,052,836 digits long and will enter Chris Caldwell's “The Largest Known Primes Database” (http://primes.utm.edu/primes) ranked 51st overall. This prime is also a Generalized Fermat prime and ranks as the 12th largest found. The discovery was made by Heinz Ming of Switzerland using an Intel Core(TM) i7 CPU 860 @ 2.80GHz with 8GB RAM, running Windows 7 Professional. This computer took just over 5 hours 59 minutes to complete the primality test using LLR. Heinz is a member of the Aggie The Pew team. The prime was verified by Tim McArdle, a member of the Don't Panic Labs team, using an AMD Athlon(tm) II P340 Dual-Core Processor with 6 GB RAM, running Windows 7 Professional. Credits for the discovery are as follows: 1. Heinz Ming (Swtzerland), discoverer 2. PrimeGrid, et al. 3. Srsieve, sieving program developed by Geoff Reynolds 4. PSieve, sieving program developed by Ken Brazier and Geoff Reynolds 5. LLR, primality program developed by Jean Penné 6. OpenPFGW, a primality program developed by Chris Nash & Jim Fougeron with maintenance and improvements by Mark Rodenkirch OpenPFGW, a primality program developed by Chris Nash & Jim Fougeron, was used to check for Fermat Number divisibility (including generalized and extended). For more information about Fermat and generalized Fermat Number divisors, please see Wilfrid Keller's sites: http://www.prothsearch.net/fermat.html http://www1.uni-hamburg.de/RRZ/W.Keller/GFNfacs.html Generalized and extended generalized Fermat number divisors discovered are as follows: 9*2^3497442+1 is a Factor of GF(3497441,7) 9*2^3497442+1 is a Factor of xGF(3497438,9,8) 9*2^3497442+1 is a Factor of GF(3497441,10) 9*2^3497442+1 is a Factor of xGF(3497439,11,3) 9*2^3497442+1 is a Factor of xGF(3497441,12,5) Using a single PC would have taken years to find this prime.
    [Show full text]