The Moon Tilt Illusion
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Visual Tilt Estimation for Planar-Motion Methods in Indoor Mobile Robots
robotics Article Visual Tilt Estimation for Planar-Motion Methods in Indoor Mobile Robots David Fleer Computer Engineering Group, Faculty of Technology, Bielefeld University, D-33594 Bielefeld, Germany; dfl[email protected]; Tel.: +49-521-106-5279 Received: 22 September 2017; Accepted: 28 October 2017; Published: date Abstract: Visual methods have many applications in mobile robotics problems, such as localization, navigation, and mapping. Some methods require that the robot moves in a plane without tilting. This planar-motion assumption simplifies the problem, and can lead to improved results. However, tilting the robot violates this assumption, and may cause planar-motion methods to fail. Such a tilt should therefore be corrected. In this work, we estimate a robot’s tilt relative to a ground plane from individual panoramic images. This estimate is based on the vanishing point of vertical elements, which commonly occur in indoor environments. We test the quality of two methods on images from several environments: An image-space method exploits several approximations to detect the vanishing point in a panoramic fisheye image. The vector-consensus method uses a calibrated camera model to solve the tilt-estimation problem in 3D space. In addition, we measure the time required on desktop and embedded systems. We previously studied visual pose-estimation for a domestic robot, including the effect of tilts. We use these earlier results to establish meaningful standards for the estimation error and time. Overall, we find the methods to be accurate and fast enough for real-time use on embedded systems. However, the tilt-estimation error increases markedly in environments containing relatively few vertical edges. -

Glossary Glossary
Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts. -
Video Tripod Head
thank you for choosing magnus. One (1) year limited warranty Congratulations on your purchase of the VPH-20 This MAGNUS product is warranted to the original purchaser Video Pan Head by Magnus. to be free from defects in materials and workmanship All Magnus Video Heads are designed to balance under normal consumer use for a period of one (1) year features professionals want with the affordability they from the original purchase date or thirty (30) days after need. They’re durable enough to provide many years replacement, whichever occurs later. The warranty provider’s of trouble-free service and enjoyment. Please carefully responsibility with respect to this limited warranty shall be read these instructions before setting up and using limited solely to repair or replacement, at the provider’s your Video Pan Head. discretion, of any product that fails during normal use of this product in its intended manner and in its intended VPH-20 Box Contents environment. Inoperability of the product or part(s) shall be determined by the warranty provider. If the product has • VPH-20 Video Pan Head Owner’s been discontinued, the warranty provider reserves the right • 3/8” and ¼”-20 reducing bushing to replace it with a model of equivalent quality and function. manual This warranty does not cover damage or defect caused by misuse, • Quick-release plate neglect, accident, alteration, abuse, improper installation or maintenance. EXCEPT AS PROVIDED HEREIN, THE WARRANTY Key Features PROVIDER MAKES NEITHER ANY EXPRESS WARRANTIES NOR ANY IMPLIED WARRANTIES, INCLUDING BUT NOT LIMITED Tilt-Tension Adjustment Knob TO ANY IMPLIED WARRANTY OF MERCHANTABILITY Tilt Lock OR FITNESS FOR A PARTICULAR PURPOSE. -

The Moon Illusion and Size–Distance Scaling—Evidence for Shared Neural Patterns
The Moon Illusion and Size–Distance Scaling—Evidence for Shared Neural Patterns Ralph Weidner1*, Thorsten Plewan1,2*, Qi Chen1, Axel Buchner3, Peter H. Weiss1,4, and Gereon R. Fink1,4 Abstract ■ A moon near to the horizon is perceived larger than a moon pathway areas including the lingual and fusiform gyri. The func- at the zenith, although—obviously—the moon does not change tional role of these areas was further explored in a second ex- its size. In this study, the neural mechanisms underlying the periment. Left V3v was found to be involved in integrating “moon illusion” were investigated using a virtual 3-D environ- retinal size and distance information, thus indicating that the ment and fMRI. Illusory perception of an increased moon size brain regions that dynamically integrate retinal size and distance was associated with increased neural activity in ventral visual play a key role in generating the moon illusion. ■ INTRODUCTION psia; Sperandio, Kaderali, Chouinard, Frey, & Goodale, Although the moon does not change its size, the moon 2013; Enright, 1989; Roscoe, 1989). near to the horizon is perceived as relatively larger com- One concept of size constancy scaling implies that the pared with when it is located at the zenith. This phenome- retinal image size and the estimated distance of an object non is called the “moon illusion” and is one of the oldest are conjointly considered, thereby enabling constant size visual illusions known (Ross & Plug, 2002). Despite exten- perception of objects at different distances (Kaufman & sive research, no consensus has been reached regarding Kaufman, 2000). With respect to the moon illusion, appar- the underlying perceptual and neural correlates (Ross & ent distance theories, for example, propose that “the per- Plug, 2002; Hershenson, 1989). -

Polar Winds from VIIRS
Polar Winds from VIIRS Jeff Key*, Richard Dworak+, Dave Santek+, Wayne Bresky@, Steve Wanzong+ ! Jaime Daniels#, Andrew Bailey@, Chris Velden+, Hongming Qi^, Pete Keehn#, Walter Wolf#! ! *NOAA/National Environmental Satellite, Data, and Information Service, Madison, WI! + Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin-Madison! #NOAA/National Environmental Satellite, Data, and Information Service, Camp Springs, MD! ^NOAA/National Environmental Satellite, Data, and Information Service, Camp Springs, MD! @I.M. Systems Group (IMSG), Rockville, MD USA! 11th International Winds Workshop, Auckland, 20-24 February 2012 The Polar Wind Product Suite MODIS Polar Winds LEO-GEO Polar Winds •" Aqua and Terra separately, bent pipe •" Combination of may geostationary data source Operational and polar-orbiting imagers •" Aqua and Terra combined, bent pipe •" Fills the 60-70 degree latitude gap •" Direct broadcast (DB) at EW –" McMurdo, Antarctica (Terra, Aqua) VIIRS Polar Winds –" Tromsø, Norway (Terra only) •" (Details on following slides) –" Sodankylä, Finland (Terra only) –" Fairbanks, Alaska (Terra, from UAF) EW AVHRR Polar Winds •" Global Area Coverage (GAC) for NOAA-15, -16, -17, -18, -19 Operational •" Metop Operational •" HRPT (High Resolution Picture Transmission = direct readout) at –" Barrow, Alaska, NOAA-16, -17, -18, -19 –" Rothera, Antarctica, NOAA-17, -18, -19 •" Historical GAC winds, 1982-2009. Two satellites throughout most of the time series. Polar Wind Product History Operational NWP Users of Polar Winds! 13 NWP centers in 9 countries: •" European Centre for Medium-Range Weather Forecasts (ECMWF) - since Jan 2003.! •" NASA Global Modeling and Assimilation Office (GMAO) - since early 2003.! •" Deutscher Wetterdienst (DWD) – MODIS since Nov 2003. DB and AVHRR.! •" Japan Meteorological Agency (JMA), Arctic only - since May 2004.! •" Canadian Meteorological Centre (CMC) – since Sep 2004. -

Surface Tilt (The Direction of Slant): a Neglected Psychophysical Variable
Perception & Psychophysics 1983,33 (3),241-250 Surface tilt (the direction of slant): A neglected psychophysical variable KENT A. STEVENS Massachusetts InstituteofTechnology, Cambridge, Massachusetts Surface slant (the angle between the line of sight and the surface normal) is an important psy chophysical variable. However, slant angle captures only one of the two degrees of freedom of surface orientation, the other being the direction of slant. Slant direction, measured in the image plane, coincides with the direction of the gradient of distance from viewer to surface and, equivalently, with the direction the surface normal would point if projected onto the image plane. Since slant direction may be quantified by the tilt of the projected normal (which ranges over 360 deg in the frontal plane), it is referred to here as surfacetilt. (Note that slant angle is mea sured perpendicular to the image plane, whereas tilt angle is measured in the image plane.) Com pared with slant angle's popularity as a psychophysical variable, the attention paid to surface tilt seems undeservedly scant. Experiments that demonstrate a technique for measuring ap parent surface tilt are reported. The experimental stimuli were oblique crosses and parallelo grams, which suggest oriented planes in SoD. The apparent tilt of the plane might beprobed by orienting a needle in SoD so as to appear normal, projecting the normal onto the image plane, and measuring its direction (e.g., relative to the horizontal). It is shown to be preferable, how ever, to merely rotate a line segment in 2-D, superimposed on the display, until it appears nor mal to the perceived surface. -

Rethinking Coalitions: Anti-Pornography Feminists, Conservatives, and Relationships Between Collaborative Adversarial Movements
Rethinking Coalitions: Anti-Pornography Feminists, Conservatives, and Relationships between Collaborative Adversarial Movements Nancy Whittier This research was partially supported by the Center for Advanced Study in Behavioral Sciences. The author thanks the following people for their comments: Martha Ackelsberg, Steven Boutcher, Kai Heidemann, Holly McCammon, Ziad Munson, Jo Reger, Marc Steinberg, Kim Voss, the anonymous reviewers for Social Problems, and editor Becky Pettit. A previous version of this paper was presented at the 2011 Annual Meetings of the American Sociological Association. Direct correspondence to Nancy Whittier, 10 Prospect St., Smith College, Northampton MA 01063. Email: [email protected]. 1 Abstract Social movements interact in a wide range of ways, yet we have only a few concepts for thinking about these interactions: coalition, spillover, and opposition. Many social movements interact with each other as neither coalition partners nor opposing movements. In this paper, I argue that we need to think more broadly and precisely about the relationships between movements and suggest a framework for conceptualizing non- coalitional interaction between movements. Although social movements scholars have not theorized such interactions, “strange bedfellows” are not uncommon. They differ from coalitions in form, dynamics, relationship to larger movements, and consequences. I first distinguish types of relationships between movements based on extent of interaction and ideological congruence and describe the relationship between collaborating, ideologically-opposed movements, which I call “collaborative adversarial relationships.” Second, I differentiate among the dimensions along which social movements may interact and outline the range of forms that collaborative adversarial relationships may take. Third, I theorize factors that influence collaborative adversarial relationships’ development over time, the effects on participants and consequences for larger movements, in contrast to coalitions. -

Tilt Anisoplanatism in Laser-Guide-Star-Based Multiconjugate Adaptive Optics
A&A 400, 1199–1207 (2003) Astronomy DOI: 10.1051/0004-6361:20030022 & c ESO 2003 Astrophysics Tilt anisoplanatism in laser-guide-star-based multiconjugate adaptive optics Reconstruction of the long exposure point spread function from control loop data R. C. Flicker1,2,F.J.Rigaut2, and B. L. Ellerbroek2 1 Lund Observatory, Box 43, 22100 Lund, Sweden 2 Gemini Observatory, 670 N. A’Ohoku Pl., Hilo HI-96720, USA Received 22 August 2002 / Accepted 6 January 2003 Abstract. A method is presented for estimating the long exposure point spread function (PSF) degradation due to tilt aniso- planatism in a laser-guide-star-based multiconjugate adaptive optics systems from control loop data. The algorithm is tested in numerical Monte Carlo simulations of the separately driven low-order null-mode system, and is shown to be robust and accurate with less than 10% relative error in both H and K bands down to a natural guide star (NGS) magnitude of mR = 21, for a symmetric asterism with three NGS on a 30 arcsec radius. The H band limiting magnitude of the null-mode system due to NGS signal-to-noise ratio and servo-lag was estimated previously to mR = 19. At this magnitude, the relative errors in the reconstructed PSF and Strehl are here found to be less than 5% and 1%, suggesting that the PSF retrieval algorithm will be applicable and reliable for the full range of operating conditions of the null-mode system. Key words. Instrumentation – adaptive optics – methods – statistical 1. Introduction algorithms is much reduced. Set to amend the two failings, to increase the sky coverage and reduce anisoplanatism, are 1.1. -

Libration of Venus and Mercury. Projections on the Terminator Of
Projections on the Terminator of Mars and Martian Meteorology Item Type Article Authors Douglass, A.E. Download date 24/09/2021 13:15:20 Link to Item http://hdl.handle.net/10150/200042 3406 Lastly : the relative visibility of some of the markings the limb. As of two markings occupying the same part of changes with their position with regard to the observer. the disk, Hermione regio and Somnus regio for example, For instance Somnus regio, which was almost invisible when the one will change in one way, the other in an opposite in the centre of the disk, has grown more conspicuous as manner, the changes cannot be a matter of obscuration. it has approached the limb. Anteros regio and Adonis Secondly as the position of the markings has not shifted regio have similarly become less salient on nearing the with regard to the Sun, the change cannot be intrinsic. It central meridian. Other markings under like conditions of is due probably to a difference in the character of the rock position and illumination have not done so, but have re or soil, greater or less roughness for example, in one region mained as evident in the one aspect as in the other or, than in toe other. That in these markings we are looking down m Hermione regio, have been less conspicuous on nearing on a bare desert-like surface is what the observations imply. Lowell Observatory, I896 Oct. 21. Percival Lowell. Zusatz. Die von Herrn P. Lowell eingesandten Zeich to 2h2m, Oct.8 2hi9m-25m, Oct.8 4h42m, Oct.9 1h59m nungen, zu we\chen nachtraglich noch einige spatere, bis to 2h28"', Oct.9 2h48m-56m, Oct.9 4h5om-57m, Oct.9 zum 9· November reichende hinzugetreten sind, sind zum 5h3m-8m, Oct.I6 OhiSm-20m, Oct.16 sh-5hsm, Oct.q grosseren Theil auf den beiliegenden Tafeln wiedergegeben. -

Depth of Field in Photography
Instructor: N. David King Page 1 DEPTH OF FIELD IN PHOTOGRAPHY Handout for Photography Students N. David King, Instructor WWWHAT IS DDDEPTH OF FFFIELD ??? Photographers generally have to deal with one of two main optical issues for any given photograph: Motion (relative to the film plane) and Depth of Field. This handout is about Depth of Field. But what is it? Depth of Field is a major compositional tool used by photographers to direct attention to specific areas of a print or, at the other extreme, to allow the viewer’s eye to travel in focus over the entire print’s surface, as it appears to do in reality. Here are two example images. Depth of Field Examples Shallow Depth of Field Deep Depth of Field using wide aperture using small aperture and close focal distance and greater focal distance Depth of Field in PhotogPhotography:raphy: Student Handout © N. DavDavidid King 2004, Rev 2010 Instructor: N. David King Page 2 SSSURPRISE !!! The first image (the garden flowers on the left) was shot IIITTT’’’S AAALL AN ILLUSION with a wide aperture and is focused on the flower closest to the viewer. The second image (on the right) was shot with a smaller aperture and is focused on a yellow flower near the rear of that group of flowers. Though it looks as if we are really increasing the area that is in focus from the first image to the second, that apparent increase is actually an optical illusion. In the second image there is still only one plane where the lens is critically focused. -
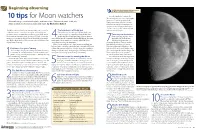
10 Tips for Moon Watchers Moon’S Brightness Are to Use High Magni- Fication Or to Add an Aperture Mask
Beginning observing You’ll find six labeled maps to help you observe the Moon at www.Astronomy.com/toc. Two other methods to reduce the 10 tips for Moon watchers Moon’s brightness are to use high magni- fication or to add an aperture mask. Mountain ranges, vast volcanic plains, and more than 1,500 named craters make the High powers restrict the field of view, Moon a target you’ll return to again and again. by Michael E. Bakich thereby reducing light throughput. An aperture mask causes your telescope to act like a much smaller instrument, but The Moon offers something for every amateur astronomer. It’s The terminator will help you at the same focal length. visible somewhere in the sky most nights, its changing face During the two favorable periods described in #3, presents features one night not seen the previous night, and it point your telescope anywhere along the line that Turn on your best vision doesn’t take an expensive setup to enjoy it. To help you get the divides the Moon’s light and dark portions. Astrono- Some years ago, my late observ- most out of viewing the Moon, I’ve developed these 10 simple 4mers call this line the terminator. Before Full Moon, the termi- ing buddy Jeff Medkeff intro- tips. Follow them, and you’ll be on your way to a lifetime of sat- nator marks where sunrise is occurring. After Full Moon, duced me to a better way of isfying lunar observing. sunset happens along the terminator. 7observing the Moon: Turn on a white Here you can catch the tops of mountains protruding just light behind you when you observe high enough to catch the Sun’s light while surrounded by lower between Quarter and Full phases. -

Dawn/Dusk Asymmetry of the Martian Ultraviolet Terminator Observed Through Suprathermal Electron Depletions Morgane Steckiewicz, P
Dawn/dusk asymmetry of the Martian UltraViolet terminator observed through suprathermal electron depletions Morgane Steckiewicz, P. Garnier, R. Lillis, D. Toublanc, François Leblanc, D. L. Mitchell, L. Andersson, Christian Mazelle To cite this version: Morgane Steckiewicz, P. Garnier, R. Lillis, D. Toublanc, François Leblanc, et al.. Dawn/dusk asymme- try of the Martian UltraViolet terminator observed through suprathermal electron depletions. Journal of Geophysical Research Space Physics, American Geophysical Union/Wiley, 2019, 124 (8), pp.7283- 7300. 10.1029/2018JA026336. insu-02189085 HAL Id: insu-02189085 https://hal-insu.archives-ouvertes.fr/insu-02189085 Submitted on 29 Mar 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. RESEARCH ARTICLE Dawn/Dusk Asymmetry of the Martian UltraViolet 10.1029/2018JA026336 Terminator Observed Through Suprathermal Key Points: • The approximate position of the Electron Depletions UltraViolet terminator can be M. Steckiewicz1 , P. Garnier1 , R. Lillis2 , D. Toublanc1, F. Leblanc3 , D. L. Mitchell2 , determined