CNI-Working Paper No. 2006-14 Does Competition for the Field Improve
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
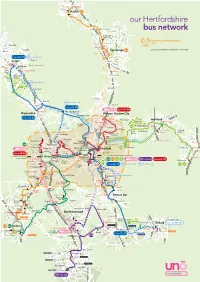
Uno Herts Network Map MASTER A3 UH Zone
Sainsbury’s Hitchin Walsworth Waitrose Road Queens St Asda Hitchin 635 Park St London Rd A602 A1(M) our Hertfordshire A602 Sainsbury’s Lister Hosptal bus network A602 Martins Way A1(M) Stevenage Old Town L y High St n t University of Hertfordshire o n Fairlands Way W zone 1 a Barnfield y Tesco Stevenage Monkswood Way Stopsley 635 zone 2 is everywhere else shown on this map Biscot Asda Stevenage North Hertfordshire College school days only 610 612 Stevenage FC Wigmore A602 A602 Luton Tesco B roa Luton NON STOP dw ate The Mall London Luton Airport r Cres Park Town A1(M) Matalan New Luton Airport Parkway Town Knebworth London Rd Capability Knebworth Stockwood Park Green B653 612 school days only Luton Hoo East Hyde Oaklands A1081 A1(M) L Welwyn NON STOP ut on R d Batford 612 school days only Sainsbury’s Lower Luton Rd Digswell 610 Station Rd Waitrose 601 653 Harpenden High St Wheathampstead Harpenden St Albans Rd l Welwyn Garden City l i Bro Marford Rd ck H Marshalls Heath s wood Ln Oaklands College e A1(M) 610 h B653 T H e Panshanger Hertford ro n Panshanger Welwyn Garden sw Hertford East o Park A414 City od R Cromer d 612 d Road Hertford h R Hyde Ln Green g Broadwater Hertingfordbury London Rd A1081 u 641 North Gascoyne school days only ro Peartree Way o High St b n Hall Grove ta HCC County Hall S Ho s Birch Green Hertford wland Cole Bullocks Lane Heath en Ln Stanborough Chequers Gre New QEII Green Sandridge rs Lakes Rd Ware pe Hospital London Rd oo C Mill tford Rd Cavan Drive Hatfield Ave Green Her St Albans Rd Jersey Farm Tesco Sandringham -

Further Information Some Facts About Us Expanding the Business
some facts about us 6,000,000 passenger journeys per year 2,700,000 miles operated a year 1,000,000 students carried a year Over 200 members of staff 90 buses over 40 routes The Company is acknowledged as one of the leading experts in assessing and meeting the public transport needs of Universities in the UK. further information expanding the business Scott Copsey UNO has continued to grow since its inception from Centre for Sustainable Communities 15 buses to 90 buses over the past 15 years University of Hertfordshire and has most recently taken over the St Albans Hatfield operations of Centrebus, adding to the company’s AL10 9AB presence in the historic city. In 2010 UNO have successfully secured a UK 01707 286035 government grant for a Green Bus Fund to buy two hybrid buses to add to the ever growing [email protected] UNO fleet, along with the introduction of ‘real time’ bus information so passengers will know exactly Jim Thorpe where their bus is. Uno As well as this UNO have also introduced ‘mobile Gypsy Moth Avenue Hatfield ticketing’ for the University of Hertfordshire AL10 9BS park&ride scheme, so making it quicker, easier and more convenient for passengers to purchase 01707 255762 their ticket . This will be introduced throughout the rest of the UNO network over the coming year. [email protected] www.unobus.info interested in setting benefits to your up an UNO style university or college bus operation for your Having your own bus company can reap huge university or college? benefits for your University/College and local community: The first stage would be for the experts at UNO U develop routes that suit your needs to assess the travel needs of your institution. -

Appendix A: List of Stakeholders That Responded to the ULEZ Consultation
Appendix B (2) Appendix A: List of stakeholders that responded to the ULEZ consultation Air Quality Brentford Coulsdon & Purley Road User Alliance of British Drivers Forum Arriva Cross River Partnership Balfour Beatty Disabled Motoring UK Bambos Charalambous MP Federation of British Historic Barking and Dagenham and Vehicle Clubs Havering Green Party Federation of Small Businesses Barnet Green Party Forest Hill Society Better Streets for Enfield Freight Transport Association Bloomsbury Air Friends of the Earth Brentford Chamber of Gipsy Hill Green Party Commerce Greenpeace Brentford Community Council Greenwich Conservatives Brewery Logistics Group Heart of London Business British Heart Foundation Alliance British Lung Foundation Herne Hill Green Party British Motorcyclists Federation Hertfordshire County Council British Vehicle Rental and Hounslow and Brentford Leasing Association (BVRLA) Friends of the Earth Builders Merchants Federation Islington Green Party Campaign for Better Transport Joanne McCartney AM Campaign for Better Transport John Lewis Partnership (London Group) Kingston Environment Forum Campaign to Protect Rural Lambeth for a Cool Planet England Lambeth Green Party Caroline Pidgeon AM LEVC Caroline Russell AM Lewisham Cyclists Chartered Institute of Lewisham Liberal Democrats Environmental Health Licensed Taxi Drivers' Chiswick Liberal Democrats Association (LTDA) Church of England (Diocese of Living Streets Chelmsford) London Assembly Environment City of London Committee -

Back to the Floor
00 Arriva NOW! December 2009 3 Back to the floor MEETING and exceeding customers’ expectations is a priority at Arriva and National Customer Service Week (NCSW) provided the perfect opportunity to demonstrate this. Highlighting how important good customer care is for the business was just one of the benefits of NCSW, which was held from 5-9 October. It was also a chance for Arriva’s excellent customer service to shine. It was the first time Arriva had taken part in the national event and the newly centralised customer service team at Aintree and Luton used Customer service advisor Steve Byrne with operations manager Mark Brack. the occasion to organise a range of events and activities. Cross-team quizzes, a dress-down day at Aintree and a colour-themed day at Luton were just a few of the highlights. The Institute of Customer Service visited Luton, and managers from across the business went “back to the floor”. Feedback In Glasgow, Leeds, Middlesbrough, Wakefield and Whitby managers and directors joined passengers on Arriva’s buses to get face-to-face feedback. Managers and directors also took to the phones to listen to what customers had to say. Mark Brack, operations manager at Arriva North West’s St Helens’ garage, was just one of the managers who went “back to the floor” and says he found it to be a very helpful and interesting experience. Mark spent several hours with customer service advisor Steve Byrne at Aintree and was impressed with the professionalism of the team. Bob Winnington, Institute of Customer Service director, left, and customer service manager Linsey Frostick, right, He said: “I really admire the team’s knowledge, present Luton customer service advisor Dainh Danzine with a prize. -

Implementing Public Transport Smart
This work has been submitted to NECTAR, the Northampton Electronic Collection of Theses and Research. Conference or Workshop Item Title: Enhancing rural public transport accessibility through implementing a smart scan on mticketing solution: a United Kingdom case study approach within deregulated environments Creators: Copsey, S., Southern, R., Fassam, L., Denny, S., Sykes, J., Cecil, J., Walsh, S. and Joseph, S. Example citation: Copsey, S., Southern, R., Fassam, L., Denny, S., Sykes, J., Cecil, J., Walsh, S. and Joseph, S. (2016) Enhancing rural public transport accessibility through implementing a smart scanon mticketing solution: a United Kingdom case study approach within deregulated environments. Paper presented to: European Transport Conference (ETC) 2016, Barcelona, 0507 October 2016. Version: Presented version NECTARhttp://nectar.northampton.ac.uk/8894/ ENHANCING RURAL PUBLIC TRANSPORT ACCESSABILITY THROUGH IMPLEMENTING A SMART SCAN-ON M-TICKETING SOLUTION: A UNITED KINGDOM CASE STUDY APPROACH WITHIN RURAL DEREGULATED ENVIRONMENTS Dr Scott Copsey Mr John Sykes Mr Jamie Cecil Ms Sue Walsh Dr Richard Southern Department of Geography, School of Life and Medical Sciences University of Hertfordshire, UK Professor Simon Denny Mr Liam Fassam University of Northampton, UK Dr Stephen Joseph Campaign for Better Transport, UK ETC 2016 Conference Theme: What is the future for the accessibility and connectivity of rural areas? 1.0 Introduction – Context The aim of this paper is to demonstrate how two United Kingdom (UK) Local Authorities (Hertfordshire and Northamptonshire), the two Universities of Hertfordshire and Northampton and a public transport provider (UNO) have worked in partnership to develop a smart scan-on m-ticketing solution, which integrates into a wider ‘smart city’ solution delivering social good through connected value propositions. -

Getting-To-The-University.Pdf
From Stansted Airport 5 min Getting to the Walk From Luton Airport 5 min Stansted Airport Walk University Railway Station 33 min Luton Airport Bus Overground Rail Rank 10 min Tottenham Hale Shuttle Bus Train Station 5 min Walk Luton Airport Parkway From Heathrow Airport Railway Station 35 min 5 min Tottenham Hale Walk Underground Station Overground Rail 6 min Heathrow Airport Victoria Line London St Pancras Underground Station International Railway From Gatwick Airport 56 min Finsbury Park Station Piccadilly Line 10 min 5 min Underground Station Walk Walk 5 min London King's Cross Walk Gatwick Airport Underground Station London King's Cross Railway Station 10 min Finsbury Park Railway Station 60 min Walk Train Station 25 min Overground Rail Overground Rail 18 min London King's Cross Overground Rail Finsbury Park Railway Railway Station Hatfield Railway Station 25 min Hatfield Railway Station 18 min Overground Rail Station 14 min Overground Rail Uno Bus: Hatfield Railway 14 min 341/602/614/644/641/653 Uno Bus: Hatfield Railway Station 341/602/614/644/641/653 University of Station 14 min Uno Bus: Hertfordshire 14 min 341/602/614/644/641/653 University of Uno Bus: Hertfordshire 341/602/614/644/641/653 University of Hertfordshire University of Take the shuttle bus from Luton Airport Hertfordshire Walk to Stansted Airport Railway Station, to Luton Airport Parkway Railway Station located directly below the terminals > > Take the train to London St Pancras Follow signage to Heathrow Underground Take the train to Tottenham Hale Station International -

How to Get to BRE Watford
How to get to BRE Watford M1 Luton A1(m) M11 BRE’s site is 20 miles from Central London, four miles north of Stansted central Watford. We are very close to the junction of the M1 and M25 motorways. Mainline train services from London Euston pass St Albans through Watford, and London’s main airports are all within 60 M25 miles. M40 Watford BRE Junction Public transport Travelling by train Thameslink Euston The nearest mainline station to BRE is Watford Junction, on the M4 London (Euston) to Glasgow line. It is a three mile taxi ride or bus CENTRAL LONDON Heathrow journey (see below) from the station to BRE. Local services from M2 Watford Junction to St Albans call at Bricket Wood station, a 20 minute walk from BRE’s north gate. Please contact us in advance if M3 using Bricket Wood station as security will need to operate the gate M25 for you. See www.bre.co.uk/directions for more details. M20 Bus services: from bus stop 5 at Watford Junction station Gatwick M23 UNO bus service 635, from central Watford to Hitchin, stops on site at BRE. Arriva bus 321 from Watford Junction to St Albans passes Motorway Mainline rail Other rail Coach link Bus/taxi close to BRE (alight at St Michael’s School, use the underpass to reach Bucknalls Lane). See www.bre.co.uk/directions for timetables. Travelling by road Luton & From the M1 The North Leave the M1 at Junction 6 (the A405, signposted to St Albans if 6A No access to A405 approaching from London, or North Watford if approaching from St Albans the north). -

Suggested Alternative Routes During Disruption
Suggested alternative routes during disruption When Great Northern services from this station are subject to unplanned disruption, we have Issued Date: arranged for your ticket to be accepted as indicated below to get you to your destination May 2018 Suggested alternative route details from Watlington There are no practical public transport alternatives to this station. If we are unable to run trains, we will do our best to run replacement buses, however there may be a long wait. If you are able to, we advise you to make your own way to an alternative station Bus 37 runs a limited bus service Mondays to Saturdays from Watlington village centre to Downham Market Bus Stop Locations Other than those bus routes shown below you may have to buy a bus ticket and apply for a Did you know about this disruption before you got to the station? refund Become one of the thousands of people every month who get the latest information from our website The routes listed above are only suggestions. Your ticket will also be accepted on services greatnorthernrail.com/travel-information/plan-your-journey/live-departures-and-arrivals of the following operators to get to your destination: Further information and contacts Trains: Buses: Journeys via alternative routes may take longer than your normal journey or operate only at certain times. Further information will be available from the sources below: - Cross Country - Arriva 100 & 101 between Stevenage & Luton - East Midlands Trains - Arriva 300 & 301 between Hatfield & St Albans - Greater Anglia - Arriva 724 -

University of Hertfordshire Mobile Ticketing Project
University of Hertfordshire Mobile Ticketing Project U-MOB Conference Krakow, Poland th th 13 /14 March 2019 Dr Scott Copsey / Nick Reed / Dr Richard Southern County of Hertfordshire/ University . Mix of rural villages & large towns (affordability issues) . Close to London (regulated public transport environment) . Surrounded by 3 main airports . Dissected by a number of major road links . Serviced by two main bus & one main train operator (de-regulated environment) Why did the University of Hertfordshire Set Up its Own Bus Company (UNO)? . Transport links are mainly North-South with few East-West links . Sustainability: Hertfordshire has a high car owning population . Hertfordshire has relatively poor public transport (except for rail links into London) . Growth of the University of Hertfordshire. From the late 1980’s there has been a major increase in student numbers (from c.5k to c.24,600 students) . Community issues with on-street parking, perceived lack of accessibility to the University and traffic congestion . Existing transport infrastructure was not fit for purpose Who Are UNO’s Customers? . Things seemed simple back in 1992 when the University set up its own bus company (“University Bus” now called “UNO”): . Students and staff were our “customers” and the University subsidised their travel . However there were other markets out there which we could serve e.g., schools, colleges, commuters and shoppers . So, both from a financial perspective and in the interests of providing a sustainable transport solution, the University decided to serve those markets as well The UNO Bus Route Network . UNO is a major bus operator in Central Hertfordshire but its routes spread across Hertfordshire into Bedfordshire and North London . -

Launch of Smart Mobility Research Unit
Creating a Smart Transport System for a University Campus UMOB Conference Krakow, Poland 13th/14th March 2019 Dr Scott Copsey/Nick Reed/Dr Richard Southern The University of Hertfordshire . Major Higher Education institution . Large regional University . c.24,600 students and c.2,650 staff . Annual turnover of around £250m . Owns UNO buses – the University’s own bus company . 4,600 residential students but majority daily commute County of Hertfordshire/ University . Mix of rural villages & large towns (affordability issues) . Close to London (regulated public transport environment) . Surrounded by 3 main airports . Dissected by a number of major road links . Serviced by two main bus & one main train operator (de-regulated environment) Smart Mobility Research Unit (SMRU) . Launched March 2018 . Identified capabilities/offer . Terms of reference/governance . Structure, associates, etc. Building momentum/ideas with partners (including Local Authorities, Public Engagement/Charrette, Business & private sector) . ‘Living laboratory’/Smart Campus/Mobility Ecosystem SMRU brings together… . Professional Transport Aspects . (University Travel Plan/Uno Contract/ Transport Partnerships) . Research/ Consultancy . (developing national and international partners/collaboration) . Teaching . (Undergraduate/Postgraduate/Short courses) . Seminars/Workshops – . Sharing best practice Multi Disciplinary . Smart Mobility Research Unit (inter disciplinary across University/organisations) incl. Geography, Psychology Engineering & Business . UNO (currently a Bus -

County Council Funded Services Affected by the Proposal
Table A: County Council funded services affected by the proposal Service Operator Service details Affected by: Evenings Sunday 2 Arriva Hemel Hempstead Town Service Woodhall Farm - Bennetts End 3 Arriva Hemel Hempstead Town Service Chaulden - Railway Station 4 Arriva Hemel Hempstead Town Service Grovehill West - Railway Station 8 Redline / Arriva Abbots Langley - Mount Vernon Hospital 10 Redline Woodside - Holywell 16 Richmonds Coaches Royston Town Service Burns Road - Icknield Walk 53 Landmark Coaches Letchworth Town Service Lordship Estate - Wilbury Hills 55 Arriva Stevenage - Letchworth Grange Estate 80 Centrebus Stevenage - Hitchin Westmill Estate 81A Centrebus Hitchin Town Service Purwell Lane Estate - Westmill Estate 91 Landmark Coaches Letchworth - Royston 97 Arriva Arlesey - Hitchin 98 Arriva Baldock - Hitchin 101 Arriva/Uno Stevenage - Luton 242 Metroline/Uno Potters Bar/Welwyn Garden City - Waltham Cross 301 Arriva/Uno Hemel Hempstead - Stevenage 306 Sullivan Buses Borehamwood - Watford 310 Arriva Hertford - Waltham Cross 315 Centrebus Kimpton - Welwyn Garden City 320 Arriva Hemel Hempstead - Rickmansworth Berry Lane Estate 331 Arriva Royston - Hertford 351 Trustybus Hertford - Bishop's Stortford 352 Red Rose Travel Hemel Hempstead - Watford 1 Service Operator Service details Affected by: Evenings Sunday 353 Red Rose Travel Hemel Hempstead - Amersham 384 Centrebus Hertford - Stevenage 387 Red Rose Travel Tring New Mill Estate - Aldbury/Wigginton 388 Centrebus Hertford - Welwyn -

Travel Information
Travel Information ETTING O OWNSEND G T T St Albans - Hertfordshire - Barnet – Luton - Bedfordshire Townsend School takes children from many areas – close to the school in St Albans and much further away. We are very good at supporting children who join us as many come as the only person from their Primary School. Over many years we have developed great support strategies with children settling quickly and feeling welcome and happy within days of arriving. Travel to Townsend School from many areas is simple and convenient. The school is well-served by the road network, public transport and school buses. Students travel from all parts of St Albans District and from other towns and villages over a very wide area. In recent years Townsend has regularly recruited students from over 70 different primary schools and children travel daily to Townsend from a very wide area. We have had students from many areas including – Abbots Langley, Barnet, Borehamwood, Bricket Wood, Brookmans Park, Chiswell Green, Colney Heath, Dunstable, Edgware, Elstree, Enfield, Flamstead, Great Gaddesden, Harpenden, Hatfield, Hemel Hempstead, Kimpton, Kings Langley, Langleybury, Lemsford, Leverstock Green, Little Gaddesden, Luton, Markyate, North Mymms, Park Street, Potters Bar, Radlett, Redbourn, Sandridge, Shenley, South Mimms, St Albans and District, Watford, Welwyn Garden City, Wheathampstead. Please see the more detailed travel information provided over the next few pages below. Further public bus information can be obtained from the www.interlink.org.uk - or telephone