DOCSLIB.ORG

SPHERE COVERINGS, LATTICES, and TILINGS (In Low Dimensions)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
SPHERE COVERINGS, LATTICES, and TILINGS (In Low Dimensions) Technische Universitat¨ Munchen¨ Zentrum Mathematik SPHERE COVERINGS, LATTICES, AND TILINGS (in Low Dimensions) FRANK VALLENTIN Vollstandiger¨ Abdruck der von der Fakultat¨ fur¨ Mathematik der Technischen Universitat¨ Munchen¨ zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften genehmigten Dissertation. Vorsitzender: Univ.-Prof. Dr. PETER GRITZMANN Prufer¨ der Dissertation: 1. Univ.-Prof. Dr. JURGEN¨ RICHTER-GEBERT 2. Priv.-Doz. Dr. THORSTEN THEOBALD 3. o. Univ.-Prof. Dr. Dr. h.c. PETER MANFRED GRUBER Technische Universitat¨ Wien / Osterreich¨ (schriftliche Beurteilung) Prof. Dr. CHRISTINE BACHOC Universite´ de Bordeaux 1 / Frankreich (schriftliche Beurteilung) Die Dissertation wurde am 18. Juni 2003 bei der Technischen Universitat¨ Munchen¨ eingereicht und durch die Fakultat¨ fur¨ Mathematik am 26. November 2003 angenommen. Acknowledgements I want to thank everyone who helped me to prepare this thesis. This includes ALEXANDER BELOW,REGINA BISCHOFF,KLAUS BUCHNER,MATHIEU DUTOUR,CHRISTOPH ENGEL- HARDT,SLAVA GRISHUKHIN,JOHANN HARTL,VANESSA KRUMMECK,BERND STURMFELS, HERMANN VOGEL,JURGEN¨ WEBER. I would like to thank the research groups M10 and M9 at TU Munchen,¨ the Gremos at ETH Zurich,¨ and the Institute of Algebra and Geometry at Univer- sity of Dortmund for their cordial hospitality. Especially, I want to thank JURGEN¨ RICHTER-GEBERT for many interesting and helpful discus- sions, for being a constant source of motivation, and for showing me pieces and slices of his high-minded world of “Geometrie und Freiheit”; RUDOLF SCHARLAU for the kind introduction into the subject and for proposing this research topic; ACHILL SCHURMANN¨ for reading (too) many versions of the manuscript very carefully and for many, many discussions which give now the final(?) view on VORONO¨I’s reduction theory. Even more especially, I want to thank ANJA TRAFFAS for uncountable many things. Contents 1. Introduction 1 1.1. Dirichlet-Voronoi Polytopes . 1 1.2. Sphere Coverings and Sphere Packings . 2 1.3. Prerequisites . 4 1.4. Organisation of the Thesis . 4 2. VORONO¨I’s Reduction Theory 11 2.1. Delone Subdivisions . 12 2.2. Secondary Cones . 13 2.3. VORONO¨I’s Principal Domain of the First Type . 15 2.3.1. Selling Parameters . 16 2.3.2. Computation of the Secondary Cone . 17 2.3.3. SELLING’s Reduction Algorithm . 18 2.4. Bistellar Neighbours . 21 2.5. Main Theorem of VORONO¨I’s Reduction Theory . 23 2.6. Refinements and Sums . 25 2.7. Relations to the Theory of Secondary Polytopes . 27 3. Parallelohedra 29 3.1. Definition and Basic Properties . 29 3.2. VORONO¨I’s Conjecture . 30 3.3. Duality . 33 3.3.1. Definition . 33 3.3.2. Upper Bound Theorem . 34 3.3.3. Voronoi Vectors, Supporting Hyperplanes, and Facets . 34 3.3.4. Linearity and Rigidity . 35 3.4. Vonorms and Conorms . 36 3.5. Zonotopal Parallelohedra . 39 3.5.1. Definition and Basic Properties . 39 3.5.2. SEYMOUR’s Decomposition Theorem . 41 3.5.3. Delone Subdivisions, Dicings and Zonotopal Lattices . 44 4. Results in Low Dimensions 47 4.1. Dimension 1 . 48 4.2. Dimension 2 . 48 4.3. Dimension 3 . 48 4.4. Dimension 4 . 50 4.4.1. Four-Dimensional Delone Triangulations . 50 4.4.2. Vonorms and Conorms in Dimension 4 . 53 vi Contents 4.4.3. Towards a Classification . 54 4.4.4. Diagrams for Zonotopal Cases . 54 4.4.5. Diagrams for Non-Zonotopal Cases . 55 4.4.6. More Data . 61 4.5. Dimension 5 . 62 4.5.1. The Missing Delone Triangulation . 62 4.5.2. Rigid Forms in Dimension 5 . 63 4.6. Dimension 6 and Higher . 64 5. Determinant Maximization 69 5.1. The Determinant Maximization Problem . 69 5.2. Convexity of the Problem . 69 5.3. Relation to Semidefinite Programming . 70 5.4. Algorithms for the Determinant Maximization Problem . 71 6. Cayley-Menger Determinants 73 6.1. Definition and Basic Properties . 73 6.2. The Radius of the Circumsphere of a Simplex . 74 6.3. A Linear Matrix Inequality . 75 7. Solving the Lattice Covering Problem 79 7.1. A Restricted Lattice Covering Problem . 79 7.2. Interpretation of “Classical” Results . 82 8. Moments of Inertia 85 8.1. The Moment of Inertia and the Circumradius of a Simplex . 85 8.2. Linear Optimization on Equidiscriminant Surfaces . 87 8.3. A Local Lower Bound . 88 8.4. Applications . 88 8.4.1. The Lattice Covering of Ad∗ ......................... 88 8.4.2. Four-dimensional Lattice Coverings . 93 8.4.3. Invariants and Symmetry . 95 8.4.4. Navigating in the Graph of Delone Triangulations . 95 9. Results in Low Dimensions 99 9.1. Dimension 1 . 99 9.2. Dimension 2 . 99 9.3. Dimension 3 . 100 9.4. Dimension 4 . 100 9.5. Dimension 5 . 104 9.6. Dimension 6 . 105 9.6.1. The best known 6-dimensional lattice covering . 105 9.6.2. The second best known 6-dimensional lattice covering . 107 9.7. Dimension 7 . 108 9.8. Dimension 8 and Higher . 109 A. Glossary 111 A.1. Geometry of Numbers . 111 A.2. Polyhedra and Polytopes . 113 A.3. (Realizable) Oriented Matroids . 113 Chapter 1. Introduction The main subject of this thesis is the geometry of low dimensional lattices. We concentrate on two central problems: the lattice covering problem and the classification of polytopes that tile space by lattice translates. The lattice covering problem asks for the most economical way to cover d-dimensional space by equal, overlapping spheres whose centers form a lattice. Let us look at the two most prominent plane lattices together with their coverings. It is obvious that the covering which belongs to the square lattice is less economical than the one that belongs to the hexagonal lattice. The purpose of this introduction is two-fold. First, we define the rather intuitive notions we already used. We show how our future main actors, namely Dirichlet-Voronoi polytopes of lattices, come into the spotlight. Second, we give an outline of the thesis. 1.1. Dirichlet-Voronoi Polytopes A lattice L is a discrete subgroup of a d-dimensional Euclidean vector space (E; ( ; )). For any · · lattice there are always linearly independent vectors b1;:::; bn L so that they form a lattice 2 2 Chapter 1 Introduction basis, L = Zb1 Zbn. In the following we assume for simplicity and without loss of generality that n equals⊕ · · · ⊕d. The geometry of a lattice is encoded in its Dirichlet-Voronoi polytope. This is the polytope which contains all those points lying closer to the origin than to all other lattice points: DV(L; ( ; )) = x E : for all v L we have dist(x; 0) dist(x; v) : · · f 2 2 ≤ g If it is clear which scalar product we are using, we simply write DV(L). Dirichlet-Voronoi polytopes are very special polytopes. They tile E by translates of the form DV(L) + v, v L, in a face-to-face manner. They and all their facets are centrally symmetric. If one knows2 the Dirichlet-Voronoi polytope of a lattice it is easy to determine ge- ometrical information about the lattice. Its volume is the same as the lattice’s volume, i.e. the volume of a fundamental parallelotope. A fundamental parallelotope is given by a lattice basis i αibi : αi [0; 1] . The Dirichlet-Voronoi polytope’s circumsphere and the insphere give informationfP about2 coveringg respectively about packing properties. 1.2. Sphere Coverings and Sphere Packings d d A family of subsets = (Ki)i I of R , I a set of indices, is called a covering of R if each d K 2 d d point of R belongs to at least one of the sets Ki, i.e. R = i I Ki. A covering of R is a S 2 lattice covering if it is of the form (K +v)v L where L is a lattice. In summary, lattice coverings are those coverings which cover Rd by translated2 copies of a single body K and in addition the translates are the vectors of a lattice L. Although the general notion of density is very intuitive, it is not easy to give a good definition which exhibits all pathological cases (see e.g. [Kup2000]). But since we are interested only in the case of lattice coverings, pathological cases do not exist and we are fine with the following quite classical definitions. Rd r r d Let Cd(p; r) = x : maxi xi pi r = [ 2 ; 2 ] + p be a cube with side length r f 2 j − j ≤ g − d centered at p. We say that a collection = (Ki)i I of subsets of R has density ρ( ) if the limit K 2 K i I vol(Cd(0; r) Ki) lim P 2 \ r vol C (0; r) !1 d exists and if it equals ρ( ). Of course, there are cases where the limit does not exist and there are K even cases where the formula does not make any sense. But for lattice coverings (K+v)v L with 2 measurable body K there is no such problem as demonstrated in the first chapter of ROGERS’ little book [Rog1964]. There (Theorem 1.6) it is also shown that the density of a lattice covering vol K = (K + v)v L can be expressed as simple as ρ( ) = vol L where vol L is the volume of a fundamentalK parallelotope2 of the lattice L. K In the following we are only considering coverings consisting of solid spheres (balls). By d Bd(p; r) = x R : dist(x; p) r we denote the d-dimensional closed ball with center p f 2 ≤ g and radius r. A lattice L gives always a lattice covering of equal spheres (Bd(v; r))v L if the 2 radius r is large enough.
Load more

Recommended publications
  • Kissing Numbers: Surprises in Dimension Four Günter M
    Kissing numbers: Surprises in Dimension Four Günter M. Ziegler, TU Berlin The “kissing number problem” is a basic geometric problem that got its name from billards: Two balls “kiss” if they touch. The kissing number problem asks how many other balls can touch one given ball at the same time. If you arrange the balls on a pool ta- ble, it is easy to see that the answer is exactly six: Six balls just perfectly surround a given ball. Graphic: Detlev Stalling, ZIB Berlin and at the same time Vladimir I. Levenstein˘ in Russia proved that the correct, exact maximal numbers for the kissing number prob- lem are 240 in dimension 8, and 196560 in dimension 24. This is amazing, because these are also the only two dimensions where one knows a precise answer. It depends on the fact that mathemati- cians know very remarkable configurations in dimensions 8 and 24, which they call the E8 lattice and the Leech lattice, respectively. If, however, you think about this as a three-dimensional problem, So the kissing number problem remained unsolved, in particular, the question “how many balls can touch a given ball at the same for the case of dimension four. The so-called 24-cell, a four- time” becomes much more interesting — and quite complicated. In dimensional “platonic solid” of remarkable beauty (next page), fact, The 17th century scientific genius Sir Isaac Newton and his yields a configuration of 24 balls that would touch a given one in colleague David Gregory had a controversy about this in 1694 — four-dimensional space.
    [Show full text]
  • Examples of Manifolds
    Examples of Manifolds Example 1 (Open Subset of IRn) Any open subset, O, of IRn is a manifold of dimension n. One possible atlas is A = (O, ϕid) , where ϕid is the identity map. That is, ϕid(x) = x. n Of course one possible choice of O is IR itself. Example 2 (The Circle) The circle S1 = (x,y) ∈ IR2 x2 + y2 = 1 is a manifold of dimension one. One possible atlas is A = {(U , ϕ ), (U , ϕ )} where 1 1 1 2 1 y U1 = S \{(−1, 0)} ϕ1(x,y) = arctan x with − π < ϕ1(x,y) <π ϕ1 1 y U2 = S \{(1, 0)} ϕ2(x,y) = arctan x with 0 < ϕ2(x,y) < 2π U1 n n n+1 2 2 Example 3 (S ) The n–sphere S = x =(x1, ··· ,xn+1) ∈ IR x1 +···+xn+1 =1 n A U , ϕ , V ,ψ i n is a manifold of dimension . One possible atlas is 1 = ( i i) ( i i) 1 ≤ ≤ +1 where, for each 1 ≤ i ≤ n + 1, n Ui = (x1, ··· ,xn+1) ∈ S xi > 0 ϕi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n Vi = (x1, ··· ,xn+1) ∈ S xi < 0 ψi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n So both ϕi and ψi project onto IR , viewed as the hyperplane xi = 0. Another possible atlas is n n A2 = S \{(0, ··· , 0, 1)}, ϕ , S \{(0, ··· , 0, −1)},ψ where 2x1 2xn ϕ(x , ··· ,xn ) = , ··· , 1 +1 1−xn+1 1−xn+1 2x1 2xn ψ(x , ··· ,xn ) = , ··· , 1 +1 1+xn+1 1+xn+1 are the stereographic projections from the north and south poles, respectively.
    [Show full text]
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
  • Topological Modes in Dual Lattice Models
    Topological Modes in Dual Lattice Models Mark Rakowski 1 Dublin Institute for Advanced Studies, 10 Burlington Road, Dublin 4, Ireland Abstract Lattice gauge theory with gauge group ZP is reconsidered in four dimensions on a simplicial complex K. One finds that the dual theory, formulated on the dual block complex Kˆ , contains topological modes 2 which are in correspondence with the cohomology group H (K,Zˆ P ), in addition to the usual dynamical link variables. This is a general phenomenon in all models with single plaquette based actions; the action of the dual theory becomes twisted with a field representing the above cohomology class. A similar observation is made about the dual version of the three dimensional Ising model. The importance of distinct topological sectors is confirmed numerically in the two di- 1 mensional Ising model where they are parameterized by H (K,Zˆ 2). arXiv:hep-th/9410137v1 19 Oct 1994 PACS numbers: 11.15.Ha, 05.50.+q October 1994 DIAS Preprint 94-32 1Email: [email protected] 1 Introduction The use of duality transformations in statistical systems has a long history, beginning with applications to the two dimensional Ising model [1]. Here one finds that the high and low temperature properties of the theory are related. This transformation has been extended to many other discrete models and is particularly useful when the symmetries involved are abelian; see [2] for an extensive review. All these studies have been confined to hypercubic lattices, or other regular structures, and these have rather limited global topological features. Since lattice models are defined in a way which depends clearly on the connectivity of links or other regions, one expects some sort of topological effects generally.
    [Show full text]
  • The Sphere Project
    ;OL :WOLYL 7YVQLJ[ +XPDQLWDULDQ&KDUWHUDQG0LQLPXP 6WDQGDUGVLQ+XPDQLWDULDQ5HVSRQVH ;OL:WOLYL7YVQLJ[ 7KHULJKWWROLIHZLWKGLJQLW\ ;OL:WOLYL7YVQLJ[PZHUPUP[PH[P]L[VKL[LYTPULHUK WYVTV[LZ[HUKHYKZI`^OPJO[OLNSVIHSJVTT\UP[` /\THUP[HYPHU*OHY[LY YLZWVUKZ[V[OLWSPNO[VMWLVWSLHMMLJ[LKI`KPZHZ[LYZ /\THUP[HYPHU >P[O[OPZ/HUKIVVR:WOLYLPZ^VYRPUNMVYH^VYSKPU^OPJO [OLYPNO[VMHSSWLVWSLHMMLJ[LKI`KPZHZ[LYZ[VYLLZ[HISPZO[OLPY *OHY[LYHUK SP]LZHUKSP]LSPOVVKZPZYLJVNUPZLKHUKHJ[LK\WVUPU^H`Z[OH[ YLZWLJ[[OLPY]VPJLHUKWYVTV[L[OLPYKPNUP[`HUKZLJ\YP[` 4PUPT\T:[HUKHYKZ This Handbook contains: PU/\THUP[HYPHU (/\THUP[HYPHU*OHY[LY!SLNHSHUKTVYHSWYPUJPWSLZ^OPJO HUK YLÅLJ[[OLYPNO[ZVMKPZHZ[LYHMMLJ[LKWVW\SH[PVUZ 4PUPT\T:[HUKHYKZPU/\THUP[HYPHU9LZWVUZL 9LZWVUZL 7YV[LJ[PVU7YPUJPWSLZ *VYL:[HUKHYKZHUKTPUPT\TZ[HUKHYKZPUMV\YRL`SPMLZH]PUN O\THUP[HYPHUZLJ[VYZ!>H[LYZ\WWS`ZHUP[H[PVUHUKO`NPLUL WYVTV[PVU"-VVKZLJ\YP[`HUKU\[YP[PVU":OLS[LYZL[[SLTLU[HUK UVUMVVKP[LTZ"/LHS[OHJ[PVU;OL`KLZJYPILwhat needs to be achieved in a humanitarian response in order for disaster- affected populations to survive and recover in stable conditions and with dignity. ;OL:WOLYL/HUKIVVRLUQV`ZIYVHKV^ULYZOPWI`HNLUJPLZHUK PUKP]PK\HSZVMMLYPUN[OLO\THUP[HYPHUZLJ[VYH common language for working together towards quality and accountability in disaster and conflict situations ;OL:WOLYL/HUKIVVROHZHU\TILYVMºJVTWHUPVU Z[HUKHYKZ»L_[LUKPUNP[ZZJVWLPUYLZWVUZL[VULLKZ[OH[ OH]LLTLYNLK^P[OPU[OLO\THUP[HYPHUZLJ[VY ;OL:WOLYL7YVQLJ[^HZPUP[PH[LKPU I`HU\TILY VMO\THUP[HYPHU5.6ZHUK[OL9LK*YVZZHUK 9LK*YLZJLU[4V]LTLU[ ,+0;065 7KHB6SKHUHB3URMHFWBFRYHUBHQBLQGG The Sphere Project Humanitarian Charter and Minimum Standards in Humanitarian Response Published by: The Sphere Project Copyright@The Sphere Project 2011 Email: [email protected] Website : www.sphereproject.org The Sphere Project was initiated in 1997 by a group of NGOs and the Red Cross and Red Crescent Movement to develop a set of universal minimum standards in core areas of humanitarian response: the Sphere Handbook.
    [Show full text]
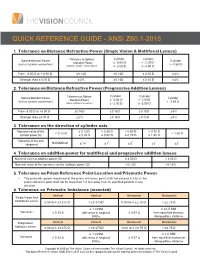
  • Quick Reference Guide - Ansi Z80.1-2015
    QUICK REFERENCE GUIDE - ANSI Z80.1-2015 1. Tolerance on Distance Refractive Power (Single Vision & Multifocal Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -4.50 D (minus cylinder convention) ≤ -2.00 D ≤ -4.50 D From - 6.50 D to + 6.50 D ± 0.13 D ± 0.13 D ± 0.15 D ± 4% Stronger than ± 6.50 D ± 2% ± 0.13 D ± 0.15 D ± 4% 2. Tolerance on Distance Refractive Power (Progressive Addition Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -3.50 D (minus cylinder convention) ≤ -2.00 D ≤ -3.50 D From -8.00 D to +8.00 D ± 0.16 D ± 0.16 D ± 0.18 D ± 5% Stronger than ±8.00 D ± 2% ± 0.16 D ± 0.18 D ± 5% 3. Tolerance on the direction of cylinder axis Nominal value of the ≥ 0.12 D > 0.25 D > 0.50 D > 0.75 D < 0.12 D > 1.50 D cylinder power (D) ≤ 0.25 D ≤ 0.50 D ≤ 0.75 D ≤ 1.50 D Tolerance of the axis Not Defined ° ° ° ° ° (degrees) ± 14 ± 7 ± 5 ± 3 ± 2 4. Tolerance on addition power for multifocal and progressive addition lenses Nominal value of addition power (D) ≤ 4.00 D > 4.00 D Nominal value of the tolerance on the addition power (D) ± 0.12 D ± 0.18 D 5. Tolerance on Prism Reference Point Location and Prismatic Power • The prismatic power measured at the prism reference point shall not exceed 0.33Δ or the prism reference point shall not be more than 1.0 mm away from its specified position in any direction.
    [Show full text]
  • Gazette Des Mathématiciens
    JUILLET 2018 – No 157 la Gazette des Mathématiciens • Autour du Prix Fermat • Mathématiques – Processus ponctuels déterminantaux • Raconte-moi... le champ libre gaussien • Tribune libre – Quelle(s) application(s) pour le plan Torossian-Villani la GazetteComité de rédaction des Mathématiciens Rédacteur en chef Sébastien Gouëzel Boris Adamczewski Université de Nantes Institut Camille Jordan, Lyon [email protected] [email protected] Sophie Grivaux Rédacteurs Université de Lille [email protected] Thomas Alazard École Normale Supérieure de Paris-Saclay [email protected] Fanny Kassel IHÉS Maxime Bourrigan [email protected] Lycée Saint-Geneviève, Versailles [email protected] Pauline Lafitte Christophe Eckès École Centrale, Paris Archives Henri Poincaré, Nancy [email protected] [email protected] Damien Gayet Romain Tessera Institut Fourier, Grenoble Université Paris-Sud [email protected] [email protected] Secrétariat de rédaction : smf – Claire Ropartz Institut Henri Poincaré 11 rue Pierre et Marie Curie 75231 Paris cedex 05 Tél. : 01 44 27 67 96 – Fax : 01 40 46 90 96 [email protected] – http://smf.emath.fr Directeur de la publication : Stéphane Seuret issn : 0224-8999 À propos de la couverture. Cette image réalisée par Alejandro Rivera (Institut Fourier) est le graphe de la partie positive du champ libre gaussien sur le tore plat 2=(2á2) projeté sur la somme des espaces propres du laplacien de valeur propre plus petite que 500. Les textures et couleurs ajoutées sur le graphe sont pure- ment décoratives. La fonction a été calculée avec C++ comme une somme de polynômes trigonométriques avec des poids aléatoires bien choisis, le graphe a été réalisé sur Python et les textures et couleurs ont été réalisées avec gimp.
    [Show full text]
  • Local Covering Optimality of Lattices: Leech Lattice Versus Root Lattice E8
    Local Covering Optimality of Lattices: Leech Lattice versus Root Lattice E8 Achill Sch¨urmann, Frank Vallentin ∗ 10th November 2004 Abstract We show that the Leech lattice gives a sphere covering which is locally least dense among lattice coverings. We show that a similar result is false for the root lattice E8. For this we construct a less dense covering lattice whose Delone subdivision has a common refinement with the Delone subdivision of E8. The new lattice yields a sphere covering which is more than 12% less dense than the formerly ∗ best known given by the lattice A8. Currently, the Leech lattice is the first and only known example of a locally optimal lattice covering having a non-simplicial Delone subdivision. We hereby in particular answer a question of Dickson posed in 1968. By showing that the Leech lattice is rigid our answer is even strongest possible in a sense. 1 Introduction The Leech lattice is the exceptional lattice in dimension 24. Soon after its discovery by Leech [Lee67] it was conjectured that it is extremal for several geometric problems in R24: the kissing number problem, the sphere packing problem and the sphere covering problem. In 1979, Odlyzko and Sloane and independently Levenshtein solved the kissing number problem in dimension 24 by showing that the Leech lattice gives an optimal solution. Two years later, Bannai and Sloane showed that it gives the unique solution up to isometries (see [CS88], Ch. 13, 14). Unlike the kissing number problem, the other two problems are still open. Recently, Cohn and Kumar [CK04] showed that the Leech lattice gives the unique densest lattice sphere packing in R24.
    [Show full text]
  • Guide to Proper Names and References in Gödel's “Protokolle
    Guide to proper names and references in Gödel’s “Protokolle” notebook People Abel Othenio Abel (1875-1946) professor of paleontology and paleobiology at the University of Vienna. Founder of the group of professors known as the “Bärenhöhle” that blocked the appointment and promotion of Jews Adele Adele Nimbursky, née Porkert (1899–1981), Gödel’s girlfriend, separated from her first husband; she and Gödel would marry in September 1938 Bachmann Friedrich Bachmann (1909–1982), mathematician, doctoral student of Scholz’s at Münster, where he received his Ph.D. in 1933; from 1935 at University of Marburg, as assistant then Privatdozent Behmann Heinrich Behmann (1891–1970), German mathematician; his reply to Perelman’s criticism of Gödel’s result had appeared in the journal Mind in April 1937. He was dismissed from his position at ​ ​ the University of Halle after the war for his Nazi Party activities Beer Gustav Beer, member of the Vienna Circle and Menger’s Mathematical Colloquium Benjamin Abram Cornelius Benjamin (1897–1968), American philosopher of science on the University of Chicago faculty 1932 to 1945 Bernays Paul Bernays (1888–1977), Swiss mathematician and logician; close collaborator with David Hilbert on the foundations of mathematics and the axiomatization of set theory Brentano Franz Brentano (1838-1917), resigned as priest, Professor of Philosophy at the University of Vienna, founder of Gestalt Brunsvick Egon Brunswik (1903–1955), Hungarian-born psychologist, assistant to Karl Bühler in Vienna, active member of Otto Neurath’s “Unity of Science” movement Bühler Karl Bühler (1879–1963), professor of psychology at the University of Vienna. He led an effort to reorganize Vienna’s city schools by incorporating scientific findings from child psychology.
    [Show full text]
  • The BEST WRITING on MATHEMATICS
    The BEST WRITING on MATHEMATICS 2012 The BEST WRITING on MATHEMATICS 2012 Mircea Pitici, Editor FOREWORD BY DAVID MUMFORD P RI NC E TO N U N IVER S I T Y P RE SS P RI NC E TO N A N D OX FORD Copyright © 2013 by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TW press.princeton.edu All Rights Reserved ISBN 978- 0- 691-15655-2 This book has been composed in Perpetua Printed on acid- free paper. ∞ Printed in the United States of America 1 3 5 7 9 10 8 6 4 2 For my parents Contents Foreword: The Synergy of Pure and Applied Mathematics, of the Abstract and the Concrete DAVID MUMFORD ix Introduction MIRCEA PITICI xvii Why Math Works MARIO LIVIO 1 Is Mathematics Discovered or Invented? TIMOTHY GOWERS 8 The Unplanned Impact of Mathematics PETER ROWLETT 21 An Adventure in the Nth Dimension BRIAN HAYES 30 Structure and Randomness in the Prime Numbers TERENCE TAO 43 The Strangest Numbers in String Theory JOHN C. BAEZ AND JOHN HUERTA 50 Mathematics Meets Photography: The Viewable Sphere DAVID SWART AND BRUCE TORRENCE 61 Dancing Mathematics and the Mathematics of Dance SARAH- MARIE BELCASTRO AND KARL SCHAFFER 79 Can One Hear the Sound of a Theorem? ROB SCHNEIDERMAN 93 Flat- Unfoldability and Woven Origami Tessellations ROBERT J. LANG 113 A Continuous Path from High School Calculus to University Analysis TIMOTHY GOWERS 129 viii Contents Mathematics Teachers’ Subtle, Complex Disciplinary Knowledge BRENT DAVIS 135 How to Be a Good Teacher Is an Undecidable Problem ERICA FLAPAN 141 How Your Philosophy of Mathematics Impacts Your Teaching BONNIE GOLD 149 Variables in Mathematics Education SUSANNA S.
    [Show full text]
  • Sphere Vs. 0°/45° a Discussion of Instrument Geometries And
    Sphere vs. 0°/45° ® Author - Timothy Mouw Sphere vs. 0°/45° A discussion of instrument geometries and their areas of application Introduction When purchasing a spectrophotometer for color measurement, one of the choices that must be made is the geometry of the instrument; that is, whether to buy a spherical or 0°/45° instrument. In this article, we will attempt to provide some information to assist you in determining which type of instrument is best suited to your needs. In order to do this, we must first understand the differences between these instruments. Simplified schematics of instrument geometries We will begin by looking at some simple schematic drawings of the two different geometries, spherical and 0°/45°. Figure 1 shows a drawing of the geometry used in a 0°/45° instrument. The illumination of the sample is from 0° (90° from the sample surface). This means that the specular or gloss angle (the angle at which the light is directly reflected) is also 0°. The fiber optic pick-ups are located at 45° from the specular angle. Figure 1 X-Rite World Headquarters © 1995 X-Rite, Incorporated Doc# CA00015a.doc (616) 534-7663 Fax (616) 534-8960 September 15, 1995 Figure 2 shows a drawing of the geometry used in an 8° diffuse sphere instrument. The sphere wall is lined with a highly reflective white substance and the light source is located on the rear of the sphere wall. A baffle prevents the light source from directly illuminating the sample, thus providing diffuse illumination. The sample is viewed at 8° from perpendicular which means that the specular or gloss angle is also 8° from perpendicular.
    [Show full text]
  • Mathematical Circus & 'Martin Gardner
    MARTIN GARDNE MATHEMATICAL ;MATH EMATICAL ASSOCIATION J OF AMERICA MATHEMATICAL CIRCUS & 'MARTIN GARDNER THE MATHEMATICAL ASSOCIATION OF AMERICA Washington, DC 1992 MATHEMATICAL More Puzzles, Games, Paradoxes, and Other Mathematical Entertainments from Scientific American with a Preface by Donald Knuth, A Postscript, from the Author, and a new Bibliography by Mr. Gardner, Thoughts from Readers, and 105 Drawings and Published in the United States of America by The Mathematical Association of America Copyright O 1968,1969,1970,1971,1979,1981,1992by Martin Gardner. All riglhts reserved under International and Pan-American Copyright Conventions. An MAA Spectrum book This book was updated and revised from the 1981 edition published by Vantage Books, New York. Most of this book originally appeared in slightly different form in Scientific American. Library of Congress Catalog Card Number 92-060996 ISBN 0-88385-506-2 Manufactured in the United States of America For Donald E. Knuth, extraordinary mathematician, computer scientist, writer, musician, humorist, recreational math buff, and much more SPECTRUM SERIES Published by THE MATHEMATICAL ASSOCIATION OF AMERICA Committee on Publications ANDREW STERRETT, JR.,Chairman Spectrum Editorial Board ROGER HORN, Chairman SABRA ANDERSON BART BRADEN UNDERWOOD DUDLEY HUGH M. EDGAR JEANNE LADUKE LESTER H. LANGE MARY PARKER MPP.a (@ SPECTRUM Also by Martin Gardner from The Mathematical Association of America 1529 Eighteenth Street, N.W. Washington, D. C. 20036 (202) 387- 5200 Riddles of the Sphinx and Other Mathematical Puzzle Tales Mathematical Carnival Mathematical Magic Show Contents Preface xi .. Introduction Xlll 1. Optical Illusions 3 Answers on page 14 2. Matches 16 Answers on page 27 3.
    [Show full text]