DOCSLIB.ORG

A Model for the Forecasting of Daily South African Rand and Nigerian Naira Exchange Rates

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Model for the Forecasting of Daily South African Rand and Nigerian Naira Exchange Rates Etuk and Amadi /International Journal of Modern Sciences and Engineering Technology (IJMSET) ISSN 2349-3755; Available at https://www.ijmset.com Volume 1, Issue 6, 2014, pp.89-97 A Model for the Forecasting of Daily South African Rand and Nigerian Naira Exchange Rates 2 Ette Harrison Etuk1 Eberechi Humphrey Amadi Department of Mathematics / Department of Mathematics / Computer Science, Rivers State Computer Science, Rivers State University of Science and University of Science and Technology, P. Harcourt, Nigeria Technology, P. Harcourt, Nigeria [email protected] [email protected] Abstract Daily South African Rand / Nigerian Naira exchange rates are analyzed by seasonal autoregressive integrated moving average (SARIMA) methods. The actual realization considered herein and called ZNER spans from 20th March 2014 to 15th September, 2014, a 180-day interval. Its time plot shows a generally negative secular trend which depicts the relative depreciation of the rand within the time interval. A seven-point differencing of the series yields a series SDZNER with a very slightly negative trend and an autocorrelation structure of a seasonal series of period 7 days. A non-seasonal differencing of the differences yields the series DSDZNER with a horizontal trend and a correlogram showing a seasonal nature of period 7days and the involvement of a seasonal moving average component of order one. There is also an indication of a seasonal autoregressive component of order two. It is noteworthy that Augmented Dickey Fuller (ADF) tests consider ZNER as non- stationary (p < .01). SDZNER is also considered non-stationary (p < .05). Only DSDZNER is considered stationary. A close look reveals the involvement of a SARIMA(0, 1, 1)X(0, 1, 1)7 component. On the overall, the models that are suggestive are (1) SARIMA(0, 1, 1)X(2, 1, 1)7 and (2) SARIMA(1, 1, 1)X(1, 1, 1)7. The later model is found to be the more adequate one on all counts. Keywords: South African Rand, Nigerian Naira, Sarima Modelling, Time Series Analysis, Foreign Exchange Rates. 1. INTRODUCTION: Foreign exchange rates have to do with the price of a country’s currency in terms of another country’s currency. International economic relations are hinged on the relative strengths of the partner nations’ currencies. This write-up is concerned with the modeling of the daily exchange rates of the South African Rand (ZAR) and the Nigerian Naira (NGN). This is with a view to providing a model which may be used to forecast the exchange rates. The modeling approach adopted is the seasonal autoregressive moving average (SARIMA) technique. The SARIMA approach to time series modeling was introduced specifically for the modeling of series that are seasonal in nature. Economic and financial time series are mostly observed to be seasonal. They have mostly been modeled using SARIMA techniques. Researchers that have adopted this approach to model some of such series are Brida and Risso (2011), Fannoh et al. (2012), Abdelghani et al. (2013), Arumugam and Anithakumari (2013), Lira(2013), AquilBurney et al. (2006), Li et al. (2013), Gharbi et al. (2011), Hassan et al. (2013), Khajavi et al. (2012), Oduro- Gyimah et al. (2012), Mombeni et al. (2013), to mention only a few. Where seasonal time series are involved SARIMA models have been observed to outdo other types of models in forecasting performance. See for instance Dagowa and Alade (2013), Sabri (2013), Qiao et al. (2013), Etuk (2014), and so on. © IJMSET-Advanced Scientific Research Forum (ASRF), All Rights Reserved “IJMSET promotes research nature, Research nature enriches the world’s future” 89 Etuk and Amadi /International Journal of Modern Sciences and Engineering Technology (IJMSET) ISSN 2349-3755; Available at https://www.ijmset.com Volume 1, Issue 6, 2014, pp.89-97 Many such exchange rates have been observed in the past to exhibit seasonal tendencies to necessitate and justify the application of such methods on them. A few of such cases are Etuk and Igbudu (2013), Etuk and Nkombou (2014), Appiah and Adetunde(2011). 2. MATERIALS AND METHODS: The data used for this work are 180 ZAR-NGN daily exchange rates from Thursday, 20th March, 2014 to Monday, 15th September, 2014 retrievable from the website www.exchangerates.org.uk/ZAR-NGN-exchange-rate-history.html . It is to be interpreted as the amount of NGN in one ZAR. 2.1. SARIMA MODELS: Suppose {Xt} is a stationary time series. It is said to follow an autoregressive moving average model of order p and q, and denoted by ARMA(p, q), if Xt - a1Xt-1 - a2Xt-2 - … - apXt-p = et + b1et-1 + b2et-2 + … + bqet-q (1) where {et} is a white noise process and the a’s and b’s are constants such that model (1) is both stationary and invertible. Model (1) may be written as A(L)Xt = B(L)et (2) 2 p 2 q k where A(L) = 1 - a1L - a2L - … - apL and B(L) = 1 + b1L + b2L + … + bqL and L Xt = Xt-k. For stationarity and invertibility of the model A(L) and B(L) must have zeroes that lie outside the unit circle respectively. Suppose the time series {Xt} is not stationary Box and Jenkins (1976) proposed that differencing of the series to an appropriate order may make the series stationary. Suppose that the th minimum order of differencing of the series for stationarity is d. The d differences of {Xt} shall be d d denoted by {Ñ Xt} where Ñ = 1 – L. If {Ñ Xt} satisfies equation (1) or (2) {Xt} is said to follow an autoregressive integrated moving average model of order p, d and q denoted by ARIMA(p, d, q). If {Xt} is seasonal of period s, Box and Jenkins (1976) further proposed that the series might be modeled by s d D s A(L)F(L )Ñ Ñ s Xt = B(L)Q(L )et (3) s where F(L) and Q(L) are polynomials in L. Ñs = 1 – L and D is the order of seasonal differencing. Then {Xt} is said to follow a multiplicative seasonal autoregressive integrated moving average model of order p, d and q denoted by SARIMA(p, d, q)X(P, D, Q)s model. 2.3. SARIMA MODEL FITTING: The fitting of the SARIMA model (3) starts with the determination of the orders p, d, q, P, D, Q and s. The seasonal period s may be suggestive from knowledge of the nature of the series as with monthly rainfall or hourly atmospheric temperature. The time plot and the correlogram could indicate a seasonal nature and therefore the value of s. The non-seasonal and the seasonal cut-off lags of the partial autocorrelation function (PACF) estimate the non-seasonal and the seasonal autoregressive (AR) orders p and P respectively. Similarly the non-seasonal and the seasonal cut-off lags of the autocorrelation function (ACF) estimate the non-seasonal and the seasonal moving average (MA) orders q and Q respectively. The non-seasonal and the seasonal differencing orders d and D are © IJMSET-Advanced Scientific Research Forum (ASRF), All Rights Reserved “IJMSET promotes research nature, Research nature enriches the world’s future” 90 Etuk and Amadi /International Journal of Modern Sciences and Engineering Technology (IJMSET) ISSN 2349-3755; Available at https://www.ijmset.com Volume 1, Issue 6, 2014, pp.89-97 often chosen such that the model is not too complex. In fact, often d + D < 3. Before and after differencing the series is tested for stationarity. This is done by the Augmented Dickey Fuller (ADF) test. Parameter estimation is invariably by the application of a nonlinear optimization technique like the least squares technique or the maximum likelihood technique. This is because of the presence in the model of values of the white noise process. After model estimation the fitted model is subjected to diagnostic checking to ascertain its goodness-of-fit to the data. This is done by residual analysis. Uncorrelatedness and/or, better still, the normality of the residuals indicates model adequacy. 3. RESULTS AND DISCUSSION: The time plot of the 180-point series ZNER in Figure 1 shows a negative secular trend. This indicates the relative decline in value of the ZAR. A 7-day differencing of ZNER yields the series SDZNER which has a slightly negative trend (See Figure 2) and a correlogram in Figure 3 which shows it is non-stationary. A non-seasonal differencing of SDZNER yields the series DSDZNER which has a horizontal trend (See Figure 4) and a correlogram in Figure 5 which suggests its stationarity. The ADF tests have the following data: ZNER test statistic is -2.80, SDZNER test statistic is -3.18 and that of DSDZNER is -9.30; the 1%, 5% and 10% critical values are -3.47, -2.88 and -2.56 respectively. That means that at p < 0.01 both ZNER and SDZNER are non-stationary and DSDZNER stationary. Moreover the correlogram of DSDZNER suggests the involvement of a seasonal MA component of order one and the involvement of a seasonal AR component of order two. It is also evident from the correlogram that the following models are possible: 1) SARIMA(0, 1, 1)X(2, 1, 1)7 and 2) SARIMA(1, 1, 1)X(1, 1, 1)7. The estimation of the SARIMA(0,1,1)X(2, 1,1)7 model of Table 1 yields: Xt + .9670Xt-7 + .4252Xt-14 = et - .0513et-1 + .4468et-7 - .1875et-8 (4) (±.1244) (±.0771) (±.0808) (±.1368) (±.0817) That of the SARIMA(1,1,1)X(1,1,1)7 model of Table 2 yields: Xt - .8922Xt-1 + .0234Xt-7 + .0147Xt-14 = et - .9596et-1 - .9482et-7 + .9132et-8 (5) (±.0409) (±.0826) (±.0824) (±.0175) (±.0182) (±.0221) where X represents DSDZNER in (4) and (5).
Load more

Recommended publications
  • NIGERIAN NAIRA EXCHANGE RATES SARIMA MODELLING Ette
    Journal of Physical Science and Innovation Volume 8, No. 1, 2016 ISSN: 2277-0119 DAILY CHINESE YUAN – NIGERIAN NAIRA EXCHANGE RATES SARIMA MODELLING Ette Harrison Etuk Department of Mathematics, Rivers State University of Science and Technology, Port Harcourt Email: [email protected] ABSTRACT A 179-point realization of daily exchange rates of the Chinese Yuan and the Nigerian Naira spanning from 18th October 2015 and 13th April 2016 is analyzed by seasonal autoregressive integrated moving average (SARIMA) methods. The time plot shows an initial downward trend up to the middle of December 2015 and then an upward trend from then onwards. This means that prior to the middle of December 2015 the Naira was relatively appreciating before it started depreciating relatively. The series is adjudged as non-stationary by the Augmented Dickey Fuller Test. A seven-point (i.e. seasonal) differencing of the series yields a series which, though adjudged stationary, still exhibits seasonality and therefore could not said to be stationary. A further (non-seasonal) differencing is done to achieve stationarity. The autocorrelation structure of the resultant series suggests the possibility of some SARIMA models. These include a SARIMA(0,1,1)x(0,1,1)12 and a SARIMA(0,1,0)x(0,1,1)12. Comparison on the basis of the information criteria AIC, Schwarz criterion and Hannan-Quinn criterion shows that the former model is the superior. It is as well observed that its residuals are white noise. Forecasting and simulation of these rates may be done on its basis. Keywords: Chinese Yuan, Nigerian Naira, SARIMA Modelling INTRODUCTION Of recent the Nigerian President Muhammadu Buhari paid a visit to China and it is being conjectured that the purpose of his visit was to discuss the possibility of a currency swap between the Chinese Yuan (CNY) and the Nigerian Naira (NGN).
    [Show full text]
  • Treasury Reporting Rates of Exchange As of December 31, 2018
    TREASURY REPORTING RATES OF EXCHANGE AS OF DECEMBER 31, 2018 COUNTRY-CURRENCY F.C. TO $1.00 AFGHANISTAN - AFGHANI 74.5760 ALBANIA - LEK 107.0500 ALGERIA - DINAR 117.8980 ANGOLA - KWANZA 310.0000 ANTIGUA - BARBUDA - E. CARIBBEAN DOLLAR 2.7000 ARGENTINA-PESO 37.6420 ARMENIA - DRAM 485.0000 AUSTRALIA - DOLLAR 1.4160 AUSTRIA - EURO 0.8720 AZERBAIJAN - NEW MANAT 1.7000 BAHAMAS - DOLLAR 1.0000 BAHRAIN - DINAR 0.3770 BANGLADESH - TAKA 84.0000 BARBADOS - DOLLAR 2.0200 BELARUS - NEW RUBLE 2.1600 BELGIUM-EURO 0.8720 BELIZE - DOLLAR 2.0000 BENIN - CFA FRANC 568.6500 BERMUDA - DOLLAR 1.0000 BOLIVIA - BOLIVIANO 6.8500 BOSNIA- MARKA 1.7060 BOTSWANA - PULA 10.6610 BRAZIL - REAL 3.8800 BRUNEI - DOLLAR 1.3610 BULGARIA - LEV 1.7070 BURKINA FASO - CFA FRANC 568.6500 BURUNDI - FRANC 1790.0000 CAMBODIA (KHMER) - RIEL 4103.0000 CAMEROON - CFA FRANC 603.8700 CANADA - DOLLAR 1.3620 CAPE VERDE - ESCUDO 94.8800 CAYMAN ISLANDS - DOLLAR 0.8200 CENTRAL AFRICAN REPUBLIC - CFA FRANC 603.8700 CHAD - CFA FRANC 603.8700 CHILE - PESO 693.0800 CHINA - RENMINBI 6.8760 COLOMBIA - PESO 3245.0000 COMOROS - FRANC 428.1400 COSTA RICA - COLON 603.5000 COTE D'IVOIRE - CFA FRANC 568.6500 CROATIA - KUNA 6.3100 CUBA-PESO 1.0000 CYPRUS-EURO 0.8720 CZECH REPUBLIC - KORUNA 21.9410 DEMOCRATIC REPUBLIC OF CONGO- FRANC 1630.0000 DENMARK - KRONE 6.5170 DJIBOUTI - FRANC 177.0000 DOMINICAN REPUBLIC - PESO 49.9400 ECUADOR-DOLARES 1.0000 EGYPT - POUND 17.8900 EL SALVADOR-DOLARES 1.0000 EQUATORIAL GUINEA - CFA FRANC 603.8700 ERITREA - NAKFA 15.0000 ESTONIA-EURO 0.8720 ETHIOPIA - BIRR 28.0400
    [Show full text]
  • The Relationship Between the South African Rand and Commodity Prices: Examining Cointegration and Causality Between the Nominal Asset Classes
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Wits Institutional Repository on DSPACE THE RELATIONSHIP BETWEEN THE SOUTH AFRICAN RAND AND COMMODITY PRICES: EXAMINING COINTEGRATION AND CAUSALITY BETWEEN THE NOMINAL ASSET CLASSES BY XOLANI NDLOVU [STUDENT NUMBER: 511531] SUPERVISOR: PROF. ERIC SCHALING RESEARCH THESIS SUBMITTED TO THE FACULTY OF COMMERCE LAW & MANAGEMENT IN PARTIAL FULFILMENT OF THE REQUIREMENTS OF THE MASTER OF MANAGEMENT IN FINANCE & INVESTMENT DEGREE UNIVERSITY OF THE WITWATERSRAND WITS BUSINESS SCHOOL Johannesburg November 2010 “We wa nt to see a competitive and stable exchange rate, nothing more, nothing less.” Tito Mboweni (8 th Governor of the SARB, 1999 -2009) 2 ABSTRACT We employ OLS analysis on a VAR Model to test the “commodity currency” hypothesis of the Rand (i.e. that the currency moves in sympathy with commodity prices) and examine the associated causality using nominal data between 1996 and 2010. We address the question of cointegration using the Engle-Granger test. We find that level series of both assets are difference stationary but not cointegrated. Further, we find the two variables negatively related with strong and significant causality running from commodity prices to the exchange rate and not vice versa, implying exogeneity to the determination of commodity prices with respect to the nominal exchange rate. The strength of the relationship is significantly weaker than other OECD commodity currencies. We surmise that the relationship is dynamic over time owing to the portfolio-rebalance argument and the Commodity Terms of Trade (CTT) effect and in the absence of an error correction mechanism, this disconnect may be prolonged.
    [Show full text]
  • Is the Botswana Pula Misaligned?
    BIDPA Working Paper 33 July 2012 Is the Botswana Pula Misaligned? Haile Taye BOTSWANA INSTITUTE FOR DEVELOPMENT POLICY ANALYSIS BIDPA The Botswana Institute for Development Policy Analysis (BIDPA) is an independent trust, which started operations in 1995 as a non-governmental policy research institution. BIDPA’s mission is to inform policy and build capacity through research and consultancy services. BIDPA is funded by the Botswana government and the African Capacity Building Foundation. BIDPA Working Paper Series The series comprises of papers which reflect work in progress or limited research efforts, which may be of interest to researchers and policy makers, or of a public education character. Working papers may already have been published elsewhere or may appear in other publications. Haile Taye is a Senior Research Fellow at the Botswana Institute for Development Policy Analysis. ISBN: 99912-65-44-9 © Botswana Institute for Development Policy Analysis, 2012 Disclaimer: The views expressed in this document are entirely those of the author and do not necessarily reflect the official opinion of BIDPA. TABLE OF CONTENTS Acknowledgements ................................................................................................. iv Abstract ................................................................................................................... iv 1. Introduction ......................................................................................................... 1 2. Determinants of the Equilibrium Exchange Rate ............................................
    [Show full text]
  • The Effects of Sentiments on the Dollar Rand (USD/ZAR) Exchange Rate
    The effects of sentiments on the dollar rand (USD/ZAR) exchange rate Kgomotso Euginia Mogotlane 772836 A research article submitted to the Faculty of Commerce, Law and Management, University of the Witwatersrand, in partial fulfilment of the requirements for the degree of Master of Business Administration Johannesburg, 2017 DECLARATION I, Kgomotso Euginia Mogotlane, declare that this research article is my own work except as indicated in the references and acknowledgements. It is submitted in partial fulfilment of the requirements for the degree of Master of Business Administration in the Graduate School of Business Administration, University of the Witwatersrand, Johannesburg. It has not been submitted before for any degree or examination in this or any other university. Kgomotso Euginia Mogotlane Signed at …………………………………………………… On the …………………………….. day of ………………………… 2017 ii DEDICATION This research article is dedicated to the memory of my angels in heaven, may your souls continue to rest in eternal peace, love and light in the presence of our Almighty. I know you always shining down on me from heaven and this is the only way I can shine back. Hope you are all proud of me. I did it for you!!! Samuel Diswantsho Mogotlane. Delia Shirley Mogotlane. Moses Willy Seponana Mogotlane. iii ACKNOWLEDGEMENTS I would like to thank God Almighty, for indeed He is faithful. Jeremiah 29:11 “For I know the plans I have for you, declares the Lord. Plans to prosper you and not harm you, plans to give you hope and a future.” I would also like to sincerely thank the following people for their assistance and support throughout my MBA journey: My supervisor, Dr Deenadayalen Konar for his assistance and guidance throughout the research process.
    [Show full text]
  • Assessing the Attractiveness of Cryptocurrencies in Relation to Traditional Investments in South Africa
    Assessing the attractiveness of cryptocurrencies in relation to traditional investments in South Africa A Dissertation presented to The Development Finance Centre (DEFIC) Graduate School of Business University of Cape Town In partial fulfilment of the requirements for the Degree of Master of Commerce in Development FinanceTown by LehlohonoloCape Letho LTHLEH001of February 2019 Supervisor: Dr Grieve Chelwa University The copyright of this thesis vests in the author. No quotation from it or information derivedTown from it is to be published without full acknowledgement of the source. The thesis is to be used for private study or non- commercial research purposes Capeonly. of Published by the University of Cape Town (UCT) in terms of the non-exclusive license granted to UCT by the author. University i PLAGIARISM DECLARATION I know that plagiarism is wrong. Plagiarism is to use another’s work and pretend that it is one’s own. I have used the American Psychological Association 6th edition convention for citation and referencing. Each contribution to, and quotation in, this dissertation from the work(s) of other people has been attributed, and has been cited and referenced. This dissertation is my own work. I have not allowed, and will not allow, anyone to copy my work with the intention of passing it off as his or her own work. I acknowledge that copying someone else’s assignment or essay, or part of it, is wrong, and declare that this is my own work. Signature________________ Date ____8 February 2019 _____________ ii ACKNOWLEDGEMENTS I would like to acknowledge my supervisor, Dr Grieve Chelwa for the thorough reviews that he provided me with on my research.
    [Show full text]
  • Modelling Naira/Pounds Exchange Rate Volatility: Application of Arima and Garch Models
    International Journal of Engineering Applied Sciences and Technology, 2019 Vol. 4, Issue 8, ISSN No. 2455-2143, Pages 238-242 Published Online December 2019 in IJEAST (http://www.ijeast.com) MODELLING NAIRA/POUNDS EXCHANGE RATE VOLATILITY: APPLICATION OF ARIMA AND GARCH MODELS Saminu Umar Shehu Sidi Abubakar Department of Mathematics and Statistics Department of Mathematics and Statistics Umaru Ali Shinkafi Polytechnic, Sokoto, Nigeria Umaru Ali Shinkafi Polytechnic, Sokoto, Nigeria Abdulrashid M. Salihu Zayyanu Umar Department of Mathematics and Statistics Department of Agricultural Science Umaru Ali Shinkafi Polytechnic, Sokoto, Nigeria Shehu Shagari Collage of Education, Sokoto, Nigeria Abstract—This study aimed at modelling the daily determined by market forces of demand and supply but rather Naira/Pound exchange rate volatility with ARIMA and the prevailing system is the managed float whereby the GARCH type models with daily exchange rate ranging from monetary authorities intervene periodically in the foreign June 2016 to July 2019 is obtained from Central Bank of exchange market of a country in order to attain some strategic Nigeria. The stationarity of the data series was checked objectives. using graphical analysis, Augmented Dickey Fuller (ADF) Time series is the record of outcomes of a variable according and Phillips-Perron (PP) tests, it was found out that the to time, the outcomes may be recorded daily, weekly, monthly, exchange rate series is not stationary, the return of the quarterly, yearly or at any other specified interval of time. It is series was obtained and found out to be stationary. It was known that time series data are volatile. Undoubtedly, daily observed that ARIMA (2, 1, 1) and GARCH (1,1) are the exchange rate of one currency for another currency forms a time optimal with the highest log-likelihood and lowest AIC and series.
    [Show full text]
  • Purchasing Power Parity Theory for Pula/Rand and Pula/Us Dollar
    2020-3704-AJBE – 18 MAY 2020 1 Purchasing Power Parity Theory For Pula/Rand and 2 Pula/Us Dollar Exchange Rates In Botswana 3 * ± 4 By Sethunya Sejoe , Narain Sinha and Zibanani Kahaka 5 6 7 Botswana is heavily dependent on mineral exports which are influenced by 8 Pula Dollar exchange rate. On the otherhand, imports in Botswana are 9 influenced by the Pula Rand exchange rate. This paper attempts to examine 10 the Purchasing Power Parity (PPP) theory considering both exchange rates 11 namely Pula/Rand and Pula/US dollar in Botswana for a period of 1976- 12 2016. Five cointegration methods have been employed to determine the 13 validity of the theory between these two exchange rates. The analysis of the 14 results showed that there was no long-run relationship between the variables 15 in both cases of Pula/Rand and Pula/US dollar exchange rates when using 16 the Engle-Granger cointegration method. Johansen cointegration test 17 inidicates one cointegrating vector. However, error correction model (ECM) 18 showed rapid deviation of the variables to the long-run equilibrium, 19 indicating a short-run cointegration relationship for Pula/Rand and Pula/US 20 dollar exchange rates. A further investigation of a long-run PPP was 21 conducted using the autoregressive distribution lag model (ARDL) bond 22 approach. The results showed that the variables were cointegrated with each 23 other for both Botswana and South Africa and between Botswana and 24 United States of America. This indicated a long-run association between the 25 variables and validated the long-run PPP theory between Botswana and 26 South Africa and between Botswana and United States of America.
    [Show full text]
  • Country Codes and Currency Codes in Research Datasets Technical Report 2020-01
    Country codes and currency codes in research datasets Technical Report 2020-01 Technical Report: version 1 Deutsche Bundesbank, Research Data and Service Centre Harald Stahl Deutsche Bundesbank Research Data and Service Centre 2 Abstract We describe the country and currency codes provided in research datasets. Keywords: country, currency, iso-3166, iso-4217 Technical Report: version 1 DOI: 10.12757/BBk.CountryCodes.01.01 Citation: Stahl, H. (2020). Country codes and currency codes in research datasets: Technical Report 2020-01 – Deutsche Bundesbank, Research Data and Service Centre. 3 Contents Special cases ......................................... 4 1 Appendix: Alpha code .................................. 6 1.1 Countries sorted by code . 6 1.2 Countries sorted by description . 11 1.3 Currencies sorted by code . 17 1.4 Currencies sorted by descriptio . 23 2 Appendix: previous numeric code ............................ 30 2.1 Countries numeric by code . 30 2.2 Countries by description . 35 Deutsche Bundesbank Research Data and Service Centre 4 Special cases From 2020 on research datasets shall provide ISO-3166 two-letter code. However, there are addi- tional codes beginning with ‘X’ that are requested by the European Commission for some statistics and the breakdown of countries may vary between datasets. For bank related data it is import- ant to have separate data for Guernsey, Jersey and Isle of Man, whereas researchers of the real economy have an interest in small territories like Ceuta and Melilla that are not always covered by ISO-3166. Countries that are treated differently in different statistics are described below. These are – United Kingdom of Great Britain and Northern Ireland – France – Spain – Former Yugoslavia – Serbia United Kingdom of Great Britain and Northern Ireland.
    [Show full text]
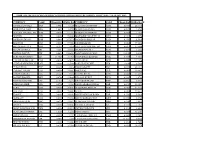
  • ZIMRA Rates of Exchange for Customs Purposes for Period 24 Dec 2020 To
    ZIMRA RATES OF EXCHANGE FOR CUSTOMS PURPOSES FOR THE PERIOD 24 DEC 2020 - 13 JAN 2021 ZWL CURRENCY CODE CROSS RATEZIMRA RATECURRENCY CODE CROSS RATEZIMRA RATE ANGOLA KWANZA AOA 7.9981 0.1250 MALAYSIAN RINGGIT MYR 0.0497 20.1410 ARGENTINE PESO ARS 1.0092 0.9909 MAURITIAN RUPEE MUR 0.4819 2.0753 AUSTRALIAN DOLLAR AUD 0.0162 61.7367 MOROCCAN DIRHAM MAD 0.8994 1.1119 AUSTRIA EUR 0.0100 99.6612 MOZAMBICAN METICAL MZN 0.9115 1.0972 BAHRAINI DINAR BHD 0.0046 217.5176 NAMIBIAN DOLLAR NAD 0.1792 5.5819 BELGIUM EUR 0.0100 99.6612 NETHERLANDS EUR 0.0100 99.6612 BOTSWANA PULA BWP 0.1322 7.5356 NEW ZEALAND DOLLAR NZD 0.0173 57.6680 BRAZILIAN REAL BRL 0.0631 15.8604 NIGERIAN NAIRA NGN 4.7885 0.2088 BRITISH POUND GBP 0.0091 109.5983 NORTH KOREAN WON KPW 11.0048 0.0909 BURUNDIAN FRANC BIF 23.8027 0.0420 NORWEGIAN KRONER NOK 0.1068 9.3633 CANADIAN DOLLAR CAD 0.0158 63.4921 OMANI RIAL OMR 0.0047 212.7090 CHINESE RENMINBI YUANCNY 0.0800 12.5000 PAKISTANI RUPEE PKR 1.9648 0.5090 CUBAN PESO CUP 0.3240 3.0863 POLISH ZLOTY PLN 0.0452 22.1111 CYPRIOT POUND EUR 0.0100 99.6612 PORTUGAL EUR 0.0100 99.6612 CZECH KORUNA CZK 0.2641 3.7860 QATARI RIYAL QAR 0.0445 22.4688 DANISH KRONER DKK 0.0746 13.4048 RUSSIAN RUBLE RUB 0.9287 1.0768 EGYPTIAN POUND EGP 0.1916 5.2192 RWANDAN FRANC RWF 12.0004 0.0833 ETHOPIAN BIRR ETB 0.4792 2.0868 SAUDI ARABIAN RIYAL SAR 0.0459 21.8098 EURO EUR 0.0100 99.6612 SINGAPORE DOLLAR SGD 0.0163 61.2728 FINLAND EUR 0.0100 99.6612 SPAIN EUR 0.0100 99.6612 FRANCE EUR 0.0100 99.6612 SOUTH AFRICAN RAND ZAR 0.1792 5.5819 GERMANY EUR 0.0100 99.6612
    [Show full text]
  • The Implications of Pegging the Botswana Pula to the U.S. Dollar
    The African e-Journals Project has digitized full text of articles of eleven social science and humanities journals. This item is from the digital archive maintained by Michigan State University Library. Find more at: http://digital.lib.msu.edu/projects/africanjournals/ Available through a partnership with Scroll down to read the article. The Implications of Pegging the Botswana Pula to the U.S. Dollar O. Ochieng INTRODUCTION The practice of peg~ing the currency of one country to another is widespread in the world: of the 141 countries in the world considered as of March 31, 1979, only 32 (23%) national currencies were not pegRed to other currencies and in Africa only 3 out of 41 were unpegGed (Tahle 1); so that the fundamental question of whether to ~eg a currency or not is already a decided matter for many countries, and what often remains to be worked out is, to which currency one should pef one's currency. Judging from the way currencies are moved from one peg to another, it seems that this issue is far from being settled. Once one has decided to peg one's currency to another, there are three policy alternatives to select from: either a country pegs to a single currency; or pegs to a specific basket of currencies; or pegs to Special Drawing Rights (SDR). Pegging a wea~ currency to a single major currency seems to ~e the option that i~ most favoured by less developed countries. The ex-colonial countries generally pegged their currencies to that of their former colonial master at independence.
    [Show full text]
  • South Africans, Cryptocurrencies and Taxation
    May 2018 Research report South Africans, Cryptocurrencies and Taxation Page 1 of 46 Page 2 of 46 CONTENTS Introduction 4 Hypotheses 5 Methodology 5 Findings 7 1. Market size 7 2. Forecast growth 9 3. Motivations for buying cryptocurrencies 11 2017: the year of “get rich quick” 11 Long term HODLers & professional curiosity 13 High-frequency traders 16 Emergency funds and goal-based savings 16 Untraceable transactions 17 4. Portfolio size and diversification 18 5. Platforms, exchanges, apps and tools 21 6. Perceptions of cryptocurrency taxation amongst investors 25 7. Perceptions of cryptocurrency taxation amongst tax professionals 28 Levels of comfort advising around tax and cryptocurrency 28 Opinions on cryptocurrency taxation 29 Risks for tax professionals 31 Data wrangling is a major pain point 32 Creating a paper trail 32 8. Taxation: the evolving regulatory framework 35 Conclusion 37 9. Demographics 38 Conclusion 42 Appendices 43 Appendix A: Research Limitations 43 Appendix B: Survey questions 44 Page 3 of 46 INTRODUCTION Introduction Although Satoshi Nakamoto’s white paper introducing the concept of Bitcoin to the world was first published a full decade ago, South African interest in cryptocurrencies was mostly confined to niche tech and finance communities. This all changed during 2017, when local interest in cryptocurrencies became stratospheric. In fact, over the past 12 months, South Africa had the highest search interest in “Bitcoin” on Google for any region in the world1. But beyond the interest, little substantive research has been done into how many South Africans are actually buying, trading and “hodling” cryptocurrencies, and why, and public understanding about how cryptocurrency behaviour is taxed.
    [Show full text]