And Smoothed Particle Hydrodynamics (SPH) Computational Techniques
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
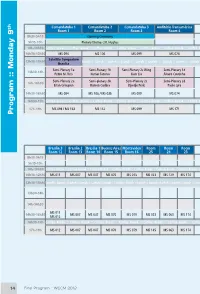
Program :: Monday 9
Comandatuba 1 Comandatuba 2 Comandatuba 3 Auditório Transamérica Una Ilhéus São Paulo 3 São Paulo 2 São Paulo 1 Quito Santiago th Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 Room 9 Room 10 Room 11 8h30-9h15 Opening Ceremony 9h15-10h Plenary Thomas J.R. Hughes 10h-10h30 Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 10h30-12h30 MS 094 MS 106 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 Satellite Symposium 12h30-13h30 Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch Brasília Semi-Plenary 1a Semi-Plenary 1b Semi-Plenary 2c Wing Semi-Plenary 1d 13h30-14h Pedro M. Reis Kumar Tamma Kam Liu Álvaro Coutinho Semi-Plenary 2a Semi-plenary 2b Semi-Plenary 2c Semi-Plenary 2d 14h-14h30 Eitan Grinspun Ramon Codina Djordje Peric Paulo Lyra 14h30-16h30 MS 094 MS 106 / MS 035 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 16h30-17h Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 17h-19h MS 094 / MS 163 MS 132 MS 099 MS 171 MS 142 / MS 005 MS 116 MS 001 MS 075 MS 085 MS 002 Program :: Monday 9 Brasília 3 Brasília 2 Brasília 1 Buenos Aires Montevideo Room Room Room Room Room Room Room Room -

14Th U.S. National Congress on Computational Mechanics
14th U.S. National Congress on Computational Mechanics Montréal • July 17-20, 2017 Congress Program at a Glance Sunday, July 16 Monday, July 17 Tuesday, July 18 Wednesday, July 19 Thursday, July 20 Registration Registration Registration Registration Short Course 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 11:30 am Registration 8:00 am - 9:30 am 8:30 am - 9:00 am OPENING PL: Tarek Zohdi PL: Andrew Stuart PL: Mark Ainsworth PL: Anthony Patera 9:00 am - 9.45 am Chair: J.T. Oden Chair: T. Hughes Chair: L. Demkowicz Chair: M. Paraschivoiu Short Courses 9:45 am - 10:15 am Coffee Break Coffee Break Coffee Break Coffee Break 9:00 am - 12:00 pm 10:15 am - 11:55 am Technical Session TS1 Technical Session TS4 Technical Session TS7 Technical Session TS10 Lunch Break 11:55 am - 1:30 pm Lunch Break Lunch Break Lunch Break CLOSING aSPL: Raúl Tempone aSPL: Ron Miller aSPL: Eldad Haber 1:30 pm - 2:15 pm bSPL: Marino Arroyo bSPL: Beth Wingate bSPL: Margot Gerritsen Short Courses 2:15 pm - 2:30 pm Break-out Break-out Break-out 1:00 pm - 4:00 pm 2:30 pm - 4:10 pm Technical Session TS2 Technical Session TS5 Technical Session TS8 4:10 pm - 4:40 pm Coffee Break Coffee Break Coffee Break Congress Registration 2:00 pm - 8:00 pm 4:40 pm - 6:20 pm Technical Session TS3 Poster Session TS6 Technical Session TS9 Reception Opening in 517BC Cocktail Coffee Breaks in 517A 7th floor Terrace Plenary Lectures (PL) in 517BC 7:00 pm - 7:30 pm Cocktail and Banquet 6:00 pm - 8:00 pm Semi-Plenary Lectures (SPL): Banquet in 517BC aSPL in 517D 7:30 pm - 9:30 pm Viewing of Fireworks bSPL in 516BC Fireworks and Closing Reception Poster Session in 517A 10:00 pm - 10:30 pm on 7th floor Terrace On behalf of Polytechnique Montréal, it is my pleasure to welcome, to Montreal, the 14th U.S. -

Analysis-Guided Improvements of the Material Point Method
ANALYSIS-GUIDED IMPROVEMENTS OF THE MATERIAL POINT METHOD by Michael Dietel Steffen A dissertation submitted to the faculty of The University of Utah in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Computing School of Computing The University of Utah December 2009 Copyright c Michael Dietel Steffen 2009 ° All Rights Reserved THE UNIVERSITY OF UTAH GRADUATE SCHOOL SUPERVISORY COMMITTEE APPROVAL of a dissertation submitted by Michael Dietel Steffen This dissertation has been read by each member of the following supervisory committee and by majority vote has been found to be satisfactory. Chair: Robert M. Kirby Martin Berzins Christopher R. Johnson Steven G. Parker James E. Guilkey THE UNIVERSITY OF UTAH GRADUATE SCHOOL FINAL READING APPROVAL To the Graduate Council of the University of Utah: I have read the dissertation of Michael Dietel Steffen in its final form and have found that (1) its format, citations, and bibliographic style are consistent and acceptable; (2) its illustrative materials including figures, tables, and charts are in place; and (3) the final manuscript is satisfactory to the Supervisory Committee and is ready for submission to The Graduate School. Date Robert M. Kirby Chair, Supervisory Committee Approved for the Major Department Martin Berzins Chair/Dean Approved for the Graduate Council Charles A. Wight Dean of The Graduate School ABSTRACT The Material Point Method (MPM) has shown itself to be a powerful tool in the simulation of large deformation problems, especially those involving complex geometries and contact where typical finite element type methods frequently fail. While these large complex problems lead to some impressive simulations and so- lutions, there has been a lack of basic analysis characterizing the errors present in the method, even on the simplest of problems. -

Scalable Large-Scale Fluid-Structure Interaction Solvers in the Uintah Framework Via Hybrid Task-Based Parallelism Algorithms
1 Scalable Large-scale Fluid-structure Interaction Solvers in the Uintah Framework via Hybrid Task-based Parallelism Algorithms Qingyu Meng, Martin Berzins UUSCI-2012-004 Scientific Computing and Imaging Institute University of Utah Salt Lake City, UT 84112 USA May 7, 2012 Abstract: Uintah is a software framework that provides an environment for solving fluid-structure interaction problems on structured adaptive grids on large-scale science and engineering problems involving the solution of partial differential equations. Uintah uses a combination of fluid-flow solvers and particle-based methods for solids, together with adaptive meshing and a novel asynchronous task-based approach with fully automated load balancing. When applying Uintah to fluid-structure interaction problems with mesh refinement, the combination of adaptive meshing and the move- ment of structures through space present a formidable challenge in terms of achieving scalability on large-scale parallel computers. With core counts per socket continuing to grow along with the prospect of less memory per core, adopting a model that uses MPI to communicate between nodes and a shared memory model on-node is one approach to achieve scalability at full machine capacity on current and emerging large-scale systems. For this approach to be successful, it is necessary to design data-structures that large numbers of cores can simultaneously access without contention. These data structures and algorithms must also be designed to avoid the overhead involved with locks and other synchronization primitives when running on large number of cores per node, as contention for acquiring locks quickly becomes untenable. This scalability challenge is addressed here for Uintah, by the development of new hybrid runtime and scheduling algorithms combined with novel lockfree data structures, making it possible for Uintah to achieve excellent scalability for a challenging fluid-structure problem with mesh refinement on as many as 260K cores. -

The Material-Point Method for Granular Materials
Comput. Methods Appl. Mech. Engrg. 187 (2000) 529±541 www.elsevier.com/locate/cma The material-point method for granular materials S.G. Bardenhagen a, J.U. Brackbill b,*, D. Sulsky c a ESA-EA, MS P946 Los Alamos National Laboratory, Los Alamos, NM 87545, USA b T-3, MS B216 Los Alamos National Laboratory, Los Alamos, NM 87545, USA c Department of Mathematics and Statistics, University of New Mexico, Albuquerqe, NM 87131, USA Abstract A model for granular materials is presented that describes both the internal deformation of each granule and the interactions between grains. The model, which is based on the FLIP-material point, particle-in-cell method, solves continuum constitutive models for each grain. Interactions between grains are calculated with a contact algorithm that forbids interpenetration, but allows separation and sliding and rolling with friction. The particle-in-cell method eliminates the need for a separate contact detection step. The use of a common rest frame in the contact model yields a linear scaling of the computational cost with the number of grains. The properties of the model are illustrated by numerical solutions of sliding and rolling contacts, and for granular materials by a shear calculation. The results of numerical calculations demonstrate that contacts are modeled accurately for smooth granules whose shape is resolved by the computation mesh. Ó 2000 Elsevier Science S.A. All rights reserved. 1. Introduction Granular materials are large conglomerations of discrete macroscopic particles, which may slide against one another but not penetrate [9]. Like a liquid, granular materials can ¯ow to assume the shape of the container. -

References (In Progress)
R References (in progress) R–1 Appendix R: REFERENCES (IN PROGRESS) TABLE OF CONTENTS Page §R.1 Foreword ...................... R–3 §R.2 Reference Database .................. R–3 R–2 §R.2 REFERENCE DATABASE §R.1. Foreword Collected references for most Chapters (except those in progress) for books Advanced Finite Element Methods; master-elective and doctoral level, abbrv. AFEM Advanced Variational Methods in Mechanics; master-elective and doctoral level, abbrv. AVMM Fluid Structure Interaction; doctoral level, abbrv. FSI Introduction to Aerospace Structures; junior undergraduate level, abbrv. IAST Matrix Finite Element Methods in Statics; senior-elective and master level, abbrv. MFEMS Matrix Finite Element Methods in Dynamics; senior-elective and master level, abbrv. MFEMD Introduction to Finite Element Methods; senior-elective and master level, abbrv. IFEM Nonlinear Finite Element Methods; master-elective and doctoral level, abbrv. NFEM Margin letters are to facilitate sort; will be removed on completion. Note 1: Many books listed below are out of print. The advent of the Internet has meant that it is easier to surf for used books across the world without moving from your desk. There is a fast search “metaengine” for comparing prices at URL http://www.addall.com: click on the “search for used books” link. Amazon.com has also a search engine, which is poorly organized, confusing and full of unnecessary hype, but does link to online reviews. [Since about 2008, old scanned books posted online on Google are an additional potential source; free of charge if the useful pages happen to be displayed. Such files cannot be downloaded or printed.] Note 2. -

AN16-LS16 Abstracts
AN16-LS16 Abstracts Abstracts are printed as submitted by the authors. Society for Industrial and Applied Mathematics 3600 Market Street, 6th Floor Philadelphia, PA 19104-2688 USA Telephone: +1-215-382-9800 Fax: +1-215-386-7999 Conference E-mail: [email protected] Conference web: www.siam.org/meetings/ Membership and Customer Service: 800-447-7426 (US & Canada) or +1-215-382-9800 (worldwide) 2 2016 SIAM Annual Meeting Table of Contents AN16 Annual Meeting Abstracts ................................................4 LS16 Life Sciences Abstracts ...................................................157 SIAM Presents Since 2008, SIAM has recorded many Invited Lectures, Prize Lectures, and selected Minisymposia from various conferences. These are available by visiting SIAM Presents (http://www.siam.org/meetings/presents.php). 2016 SIAM Annual Meeting 3 AN16 Abstracts 4 AN16 Abstracts SP1 University of Cambridge AWM-SIAM Sonia Kovalevsky Lecture - Bioflu- [email protected] ids of Reproduction: Oscillators, Viscoelastic Net- works and Sticky Situations JP1 From fertilization to birth, successful mammalian repro- Spatio-temporal Dynamics of Childhood Infectious duction relies on interactions of elastic structures with a Disease: Predictability and the Impact of Vaccina- fluid environment. Sperm flagella must move through cer- tion vical mucus to the uterus and into the oviduct, where fertil- ization occurs. In fact, some sperm may adhere to oviduc- Violent epidemics of childhood infections such as measles tal epithelia, and must change their pattern -

An Educational Tool for the Material Point Method MAE 8085 Final Report
An Educational Tool for the Material Point Method MAE 8085 Final Report Jessica Bales M.S. Candidate Mechanical Engineering Department Advisor: Dr. Zhen Chen C.W. LaPierre Professor Civil Engineering Department May 2014 The undersigned, appointed by the dean of the Graduate School, have examined the report entitled AN EDUCATIONAL TOOL FOR THE MATERIAL POINT METHOD presented by Jessica Bales, a candidate for the degree of Master of Science in Mechanical and Aerospace Engineering and hereby certify that, in their opinion, it is worthy of acceptance. Professor Zhen Chen Professor Vellore Gopalaratnam Professor P. Frank Pai Acknowledgements I would like to thank my advisor, Dr. Zhen Chen for his instruction and support throughout this project. Also, Shan Jiang and Bin Wang for their guidance in the algorithm of the program. I would also like to thank Hao Peng and Glenn Smith for their MATLAB programming advice. ii Abstract The Material Point Method (MPM), a particle method designed for simulating large deformations and the interactions between different material phases, has demonstrated its potential in modern engineering applications. To promote integrated research and educational activities, a user-friendly educational tool in MATLAB is needed. In this report, the theory and algorithm of this educational tool are documented. To validate the effectiveness of the tool, both one- and two-dimensional wave and impact problems are solved using a linear elastic model. The numerical results are then compared and verified against available analytical solutions, and the numerical solutions from an existing one-dimensional MPM code and ABAQUS, a Finite Element Method based program. iii Table of Contents 1. -

Improving the Material Point Method Ming Gong
University of New Mexico UNM Digital Repository Mathematics & Statistics ETDs Electronic Theses and Dissertations 9-1-2015 Improving the Material Point Method Ming Gong Follow this and additional works at: https://digitalrepository.unm.edu/math_etds Recommended Citation Gong, Ming. "Improving the Material Point Method." (2015). https://digitalrepository.unm.edu/math_etds/17 This Dissertation is brought to you for free and open access by the Electronic Theses and Dissertations at UNM Digital Repository. It has been accepted for inclusion in Mathematics & Statistics ETDs by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected]. Ming Gong Candidate Mathematics and Statistics Department This dissertation is approved, and it is acceptable in quality and form for publication: Approved by the Dissertation Committee: Prof. Deborah Sulsky, Chair Prof. Howard L. Schreyer, Member Prof. Stephen Lau, Member Prof. Daniel Appelo, Member Prof. Paul J. Atzberger, Member i Improving the Material Point Method by Ming Gong B.S., Applied Math, Dalian Jiaotong University, 2009 B.S., Software Engineering, Dalian Jiaotong University, 2009 M.S., Applied Math, University of New Mexico, 2012 DISSERTATION Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Mathematics The University of New Mexico Albuquerque, New Mexico July, 2015 Dedication For Xuanhan, Sumei, and Zhongbao. iii Acknowledgments I would like to thank my advisor, Professor Deborah Sulsky, for her support and guidance during my study at UNM. Not only have I learned the deep knowledge in numerical methods in PDEs from her, but I have also learned to do research in gen- eral. -

Book of Abstracts
GESELLSCHAFT für ANGEWANDTE MATHEMATIK und MECHANIK e.V. INTERNATIONAL ASSOCIATION of APPLIED MATHEMATICS and MECHANICS th 88 Annual Meeting of the International Association of Applied Mathematics and Mechanics March 6-10, 2017 Weimar, Germany Foto: Bauhaus Weimar by Sailko Book of abstracts Ilmenau@Weimar www.gamm2017.de Contents 1 Plenary Lectures 3 Ludwig Prandtl Memorial Lecture ......................... 3 Richard von Mises Lectures ............................. 6 2 Minisymposia 11 M 1: Innovative Discretization Methods, Mechanical and Mathematical Inves- tigations ..................................... 11 M 2: Recent Trends in Phase-Field Modelling ................... 15 M 3: Dislocation-based Plasticity: State of the Art and Challenges ....... 21 M 4: Nonlinear Approximations for High-dimensional Problems ......... 24 M 5: Structured Preudospectra and Stability Radii: Applications and Compu- tational Issues .................................. 26 M 6: Turbulent Liquid Metal and Magnetohydrodynamic Flows ......... 28 M 7: Flow Separation and Vortical Phenomena: Simulation in Progress .... 31 3 Young Researchers’ Minisymposia 37 YR 1: Computational Shape Optimization ..................... 37 YR 2: Computational Techniques for Bayesian Inverse Problems ........ 39 YR 3: Local and Nonlocal Methods for Processing Manifolds and Point Cloud Data ....................................... 41 4 DFG Priority Programmes 45 DFG-PP 1: Turbulent Superstructures ...................... 45 DFG-PP 2: Reliable Simulation Techniques in Solid Mechanics. Development -

2MIT Conference Schedule
Conference Schedule Second M.I.T. Conference on Computational Fluid and Solid Mechanics June 17-20, 2003 The mission of the Conference: To bring together Industry and Academia and To nurture the next generation in computational mechanics This document contains the following information in this order: - Chronological List of Plenary Lectures and Sessions - Index to Sessions by Session Number - Room Allocations for Sessions - Session Details by Session Number Notes Please note the special Plenary Panel Discussion: Thursday 7:00 - 9:00pm Room: 10-250 Providing Virtual Product Development Capabilities for Industry: The Human Element Please note that in all rooms, a transparency projector and a beamer for PowerPoint presentations will be available. But for PowerPoint presentations, the presenter must bring her/his own laptop. For any questions regarding the equipment, or special requirements, please contact [email protected]. Chronological List of Plenary Lectures and Sessions Tuesday 8:45am Welcome Professor Klaus-Jürgen Bathe Opening of Conference Professor Alice P. Gast, Vice President for Research, M.I.T. Plenary Lectures Chairperson: J.W. Tedesco 9:00 - 10:30am Room: Kresge Auditorium (W16) Biological Simulations at All Scales: From Cardiovascular Hemodynamics to Protein Molecular Mechanics R.D. Kamm, M.I.T. The Role of CAE in Product Development at Ford Motor Company S.G. Kelkar and N.K. Kochhar, Ford Motor Company 10:30 - 11:00am Coffee Break 2 Chronological List of Plenary Lectures and Sessions Tuesday 11:00am - 12:30pm Computational -

Dynamic Material Point Method with Applications in Geomechanics
DYNAMIC MATERIAL POINT METHOD WITH APPLICATIONS IN GEOMECHANICS I. Jassim Deltares, Delft, The Netherlands / Institute of Geotechnics, Stuttgart University, Germany F. Hamad Deltares, Delft, The Netherlands / Institute of Geotechnics, Stuttgart University, Germany P. Vermeer Deltares, Delft, The Netherlands / Institute of Geotechnics, Stuttgart University, Germany ABSTRACT: A dynamic Material Point Method for use in Geomechanics is presented. Soil and structural bodies are represented by (material) particles, which move inside an unstructured mesh of four-noded 3-D tetrahedral elements. As such low-order elements tend to show locking for fully developed plastic flow, a strain-enhancement remedy is described. As a first example, the penetration of a drop anchor into a Mohr-Coulomb soil is considered. As both a soil body and a metal anchor are considered, an algorithm for dynamic contact is used and described. An improved type of absorbing boundaries to avoid the reflection of stress waves is also described. The second example consists of dynamic cone penetration. Finally, the example of a collapsing tunnel is considered. 1 INTRODUCTION Over the last decades the Finite Element Method (FEM) has become the standard tool of analysis in the field of solid mechanics. However, due to its reliance on a mesh, the FEM is not well suited for the treatment of extremely large deformations. To overcome the mesh dependency of the FEM, meshfree methods have been developed, for example the Element- Free Galerkin Method (Belytschko et al, 1994) and the Material Point Method (MPM). The latter might be classified as a meshfree method, a Particle-in-Cell method or an Arbitrary Lagrangian-Eulerian method (Więckowski, 2004).