Anisotropic Spreading of Bubbles on Superaerophilic Straight Trajectories Beneath a Slide in Water
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Engineering Index》检索结果
《Engineering Index》检索结果 经检索“Engineering Village 2”, 以下论文被《Ei Compendex》收录。(检索时 间 2013 年 11 月 5 日)。 <RECORD 1> Accession number:20134316890388 Title:Direct expansion method of moments for nanoparticle Brownian coagulation in the entire size regime Authors:Chen, Zhongli (1); Lin, Jianzhong (1); Yu, Mingzhou (2) Author affiliation:(1) School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 31002 7, China; (2) China Jiliang University, Hangzhou 310018, China; (3) Karlsruhe Institute of Technol ogy, Institute for Mechanical Process Engineering and Mechanisms, Karlsruhe, Germany Corresponding author:Lin, J.([email protected]) Source title:Journal of Aerosol Science Abbreviated source title:J. Aerosol Sci. Volume:67 Issue date:January 2014 Publication year:2014 Pages:28-37 Language:English ISSN:00218502 E-ISSN:18791964 CODEN:JALSB7 Document type:Journal article (JA) Publisher:Elsevier Ltd, Langford Lane, Kidlington, Oxford, OX5 1GB, United Kingdom Number of references:29 Main heading:Method of moments Controlled terms:Brownian movement - Coagulation - Nanoparticles - Parallel architectures Uncontrolled terms:Accuracy - Brownian coagulation - Brownian particles - Entire size regime - G eometric standard deviations - Lower order moments - Partial derivatives - Quadrature method of moments Classification code:931 Classical Physics; Quantum Theory; Relativity - 921 Mathematics - 802.3 C hemical Operations - 933 Solid State Physics - 761 Nanotechnology - 722 Computer Systems and Equipment - 708 Electric and Magnetic Materials -

Nome Ruolo Istituzione LI XIN Deputy Director of Division Zhejiang
Nome Ruolo Istituzione Zhejiang Department of LI XIN Deputy Director of Division Commerce Zhejiang Department of DING SHUFENG Director of the General Office Commerce Vice director of the Division of Zhejiang Department of YANG XUEFU Human Resources Commerce Researcher of the Foreign Zhejiang Provincial Department DU JIAN Affairs Office of Education Deputy Director of Confucius LIU HUI Zhejiang University Institute Office Chinese Language Teacher of MO WEIWEI China Academy of Art International College Deputy Dean of International Zhejiang University of FANG LUPING College Technology Director of International SHEN LIHUANG Zhejiang Normal University Student Office CHEN JIANPING Dean, International College Ningbo University Vice Dean of School of CHEN MINZHI Zhejiang Sci-Tech University International Education Director of International Student Admission, Dean of TIAN YE Hangzhou Dianzi University School of International Education Dean of College of JIANG BO Zhejiang Gongshang University International Education Deputy Director of WANG JIANQI International Exchange and China Jiliang University Cooperation Office Acting Dean of International Zhejiang Chinese Medical WANG YING Education College University FANG LIQING Director, International Office Zhejiang A&F University Vice Dean of School of XU DAN Wenzhou Medical University International Studies Dean, School of International Zhejiang University of Finance YU MUHONG Education and Studies and Economics Deputy Director of Zhejiang University of Science FENG SHAOZHONG International Student Affairs -

《Engineering Index》检索结果 经检索“Engineering Village 2
《Engineering Index》检索结果 经检索“Engineering Village 2”, 以下论文被《Ei Compendex》收录。(检索时 间 2014 年 2 月 25 日)。 <RECORD 1> Accession number:20140517242144 Title:Combustion flexibility of a large-scale down-fired furnace with respect to boiler load and staging conditions at partial loads Authors:Ling, Zhongqian (1); Kuang, Min (1); Zeng, Xianyang (1); Zhang, Guangxue (1) Author affiliation:(1) Institute of Thermal Engineering, China Jiliang University, Hangzhou 310018, China Corresponding author:Kuang, M.([email protected]) Source title:Energy and Fuels Abbreviated source title:Energy Fuels Volume:28 Issue:1 Issue date:January 16, 2014 Publication year:2014 Pages:725-734 Language:English ISSN:08870624 E-ISSN:15205029 CODEN:ENFUEM Document type:Conference article (CA) Publisher:American Chemical Society, 2540 Olentangy River Road, P.O. Box 3337, Columbus, OH 43210-3337, United States Number of references:31 Main heading:Coal combustion Controlled terms:Anthracite - Boiler firing - Carbon - Coal ash - Coal fired boilers - Coal industry - Fly ash - Furnaces - Gas emissions - Industrial emissions Uncontrolled terms:Asymmetric combustions - Combustion technology - Comprehensive evaluation - Exhaust gas temperatures - Gas temperature distributions - Operation conditions - Species concentration - Technology application Classification code:451.1 Air Pollution Sources - 524 Solid Fuels - 532 Metallurgical Furnaces - 614.2 Steam Power Plant Equipment and Operation - 804 Chemical Products Generally DOI:10.1021/ef402161u Database:Compendex Compilation and indexing -

Factors Influencing Epidural Anesthesia for Cesarean Section
Message from the ITME 2018 General Chairs ITME 2018 is the 9th International Conference on Information Technology in Medicine and Education. This conference will be taken place on October 19-21, 2018, in Hangzhou, Zhejiang, China. The aim of the ITME 2018 is to provide an international conference for scientific research on IT in Medicine and Education. It was Technically Co-Sponsored by IEEE Computer Society, and sponsored by China Jiliang University, Zhejiang University, Zhejiang provincial natural science foundation, Fujian University of Traditional Chinese Medicine, University of Texas at San Antonio (UTSA), Swinburne University of Technology, Australia, Iwate Prefectural University, Shandong Normal University, Xiamen University, Fuzhou University, Hunan University of Humanities, Science and Technology. ITME 2018 is the next event in a series of highly successful the International conference on IT in Medicine and Education, ITME-16 (Fuzhou, China, December 2016), ITME-15 (Huangshan, China, November 2015), ITME-14 (Jeju, Korea, July 2014), ITME-13 (Xining, China, July 2013), ITME-12 (Hokkaido, Japan, August 2012), ITME-11 (Guangzhou, China, December 2011), ITME-09 (Jinan, China, August 2009), ITME-08 (Xiamen, China, December 2008). We would like to express our special thanks go to the Program Chairs: Shaozi Li (Xiamen University, China), Ying Dai (Iwate Prefectural University, Japan), Xiangwei Zheng (Shandong Normal University, China), Jianguo Chen (China Jiliang University, China), Chen Pan (China Jiliang University, China), Zhigang Gao (Hangzhou Dianzi University, China), all program committee members and all the additional reviewers for their valuable efforts in the review process, which helped us to guarantee the highest quality of the selected papers for the conference. -

《Engineering Index》检索结果 经检索“Engineering Village 2”, 以下
《Engineering Index》检索结果 经检索“Engineering Village 2”, 以下论文被《Ei Compendex》收录。(检索时 间 2013 年 11 月 19 日)。 <RECORD 1> Accession number:20134416935836 Title:Enhancement of the sensitivity of magneto-optical fiber sensor by magnifying the birefringence of magnetic fluid film with Loyt-Sagnac interferometer Authors:Zu, Peng (1); Chan, Chi Chiu (1); Koh, Guo Wei (1); Lew, Wen Siang (2); Jin, Yongxing (3); Liew, Hwi Fen (2); Wong, Wei Chang (1); Dong, Xinyong (3) Author affiliation:(1) School of Chemical and Biomedical Engineering, Nanyang Technological University, 637457, Singapore, Singapore; (2) School of Physical and Mathematical Sciences, Nanyang Technological University, 637371, Singapore, Singapore; (3) Institute of Optoelectronic Technology, China Jiliang University, Hangzhou 310018, China Corresponding author:Chan, C.C.([email protected]) Source title:Sensors and Actuators, B: Chemical Abbreviated source title:Sens Actuators, B Chem Volume:191 Issue date:2014 Publication year:2014 Pages:19-23 Language:English ISSN:09254005 CODEN:SABCEB Document type:Journal article (JA) Publisher:Elsevier, P.O. Box 211, Amsterdam, 1000 AE, Netherlands Number of references:23 Main heading:Magnetic fluids Controlled terms:Birefringence - Fiber optic sensors - Magnetic sensors - Magnetometers - Optical fibers Uncontrolled terms:Birefringence effects - Fiber Sensor - Magnetic field sensors - Magnetic fluid films - Magneto-optical - Optical fiber sensor - Orders of magnitude - Sagnac interferometer Classification code:708.4 Magnetic Materials - 741.1 Light/Optics -
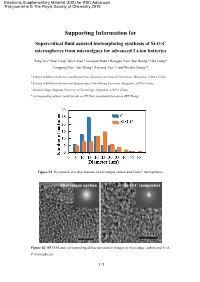
Supporting Information For
Electronic Supplementary Material (ESI) for RSC Advances. This journal is © The Royal Society of Chemistry 2016 Supporting Information for Supercritical fluid assisted biotemplating synthesis of Si-O-C microspheres from microalgaes for advanced Li-ion batteries Yang Xia,a Ruyi Fang,a Zhen Xiao,b Luoyuan Ruan,a Rongjun Yan,c Hui Huang,a Chu Liang,a Yongping Gan,a Jun Zhang,a Xinyong Tao,a,* and Wenkui Zhanga,* a College of Materials Science and Engineering, Zhejiang University of Technology, Hangzhou, 310014, China. b College of Materials Science and Engineering, China Jiliang University, Hangzhou, 310018, China. c Ocean College, Zhejiang University of Technology, Hangzhou, 310014, China. * Corresponding authors: [email protected] (XY Tao); [email protected] (WK Zhang). Figure S1 The particle size distributions of microalgae carbon and Si-O-C microspheres. Figure S2 HRTEM and corresponding diffraction pattern images of microalgae carbon and Si-O- C microspheres. 1 / 2 Figure S3 The electrochemical properties comparison of various Si-O-C materials prepared different methods. References 1. Liu, X.; Zheng, M. C.; Xie, K. Mechanism of Lithium Storage in Si-O-C Composite Anodes. J. Power Sources, 2011, 196, 10667-10672. 2. Ji, F.; Li, Y. L.; Feng, J. M.; Su, D.; Wen, Y. Y.; Feng, Y.; Hou, F. Electrochemical Performance of Graphene Nanosheets and Ceramic Composites as Anodes for Lithium Batteries. J. Mater. Chem., 2009, 19, 9063-9067. 3. Dibandjo, P.; Graczyk-Zajac, M.; Riedel, R.; Pradeep, V. S.; Soraru, G. D. Structures and Lithium Storage Performance of Si-O-C Composite Materials Depending on Pyrolysis Temperatures. -

Download GSMM 2021 Program
The 2021Global Symposium on Millimeter- GSMM 2021 Waves &THz (GSMM) May 23-26, 2021, Nanjing, Jiangsu, China 1 Organizers and Technical Co-Sponsors Zhejiang University 浙江大学 Southeast University 东南大学 Aerospace Information Research 中国科学院空天信息创新研究院 Institute, Chinese Academy of Sciences China Jiliang University 中国计量大学 Nanjing University of Science and 南京理工大学 Technology 1 TABLE OF CONTENTS SPONSORSHIP 1 WELCOME MESSAGE 3 ORGANIZING COMMITTEE 4 INTERNATIONAL STEERING COMMITTEE 5 TECHNICAL PROGRAM COMMITTEE 6 REGISTRATION 8 GENERAL INFORMATION 9 INSTRUCTIONS TO ORAL PRESENTERS 12 INSTRUCTIONS TO OVERSEA ONLINE PRESENTERS 13 TECHNICAL SESSIONS 14 2 WELCOME MESSAGE FROM THE GENERAL CHAIR AND TPC CHAIRS We are privileged and honored to warmly welcome you to the 13th Global Symposium on Millimeter- Waves &THz (in short, GSMM 2021) and the fabulous Nanjing city. This is the second time that GSMM 2021 is held in Nanjing since its inception in 2008 in Nanjing, China. The GSMM2021 was eshtablished for researchers, engineers and practitioners to present and discuss recent breakthroughs, innovations and emerging techniques in field of millimeter-wave and terahertz sensing and communications. Following the success of first GSMM 2021 event, Nanjing, China (2008), Sendai, Japan (2009), Seoul, South Korea (2010), Espoo, Finland (2011), Harbin, China (2012), Sendai, Japan (2013), Seoul, South Korea (2014), Montreal, Canada (2015) and Espoo, Finland (2016), Hongkong, China(2017), Colorado, America(2018) and Sendai. Japan(2019). The 13th GSMM 2021 is held at Nanjing, a most vibrant city with historical and cultural glory, located at the Yangtze River Delta Economic Zone next to Shanghai with world- class electronic industry and research centers. This Symposium will feature round 122 presentations during the three-day event, and the presentations cover a wide spectrum of topics ranging in millimeter-wave and terahertz sensing and communications. -

Sulfate Reduction Behavior in the Leachate Saturated Zone of Landfill
Science of the Total Environment 730 (2020) 138946 Contents lists available at ScienceDirect Science of the Total Environment journal homepage: www.elsevier.com/locate/scitotenv Sulfate reduction behavior in the leachate saturated zone of landfill sites Zhiyuan Jin a, Manting Ci a, Wenyi Yang a, Dongsheng Shen a, Lifang Hu b, Chengran Fang c, Yuyang Long a,⁎ a Zhejiang Provincial Key Laboratory of Solid Waste Treatment and Recycling, School of Environmental Science and Engineering, Zhejiang Gongshang University, Hangzhou 310012, China b College of Quality and Safety Engineering, Institution of Industrial Carbon Metrology, China Jiliang University, Hangzhou 310018, China c Key Laboratory of Recycling and Eco-treatment of Waste Biomass of Zhejiang Province, Zhejiang University of Science and Technology, Hangzhou 310023, China HIGHLIGHTS GRAPHICAL ABSTRACT • Remarkable sulfate reduction observed in leachate saturated environment. • H2S, MM, DMS emissions were most vi- olent at 50 and 60 °C. • Whole microbial structure and activity were influenced by the temperature. • dsrA and dsrB quantity decreased under higher temperatures. • Dethiobacter may contribute to higher sulfate reduction rate. article info abstract Article history: Municipal solid waste landfills are considered one of the most important parts of the sulfur cycle. However, few Received 2 April 2020 studies have focused on sulfate reduction in the leachate saturated zone, where the temperature may be variable. Received in revised form 21 April 2020 In this work, the sulfate reduction behavior was evaluated in a landfill leachate saturated zone under tempera- Accepted 22 April 2020 tures between 30 and 80 °C. The results show that microbial sulfate reduction is high in the saturated zone, es- Available online 25 April 2020 pecially when the temperature is at 50–60 °C. -

Study on the Impacts of Patent Cooperation Network in University
2nd International Conference on Economics, Social Science, Arts, Education and Management Engineering (ESSAEME 2016) Study on the Impacts of Patent Cooperation Network in University-Industry-Research Collaboration upon the Innovation Performance of University Xiaoqing Zhao1,a, WeipengLi2,b, Li Zhou3,c 1Graduate Department, Beijing Wuzi University, Beijing, China 2Graduate Department, Beijing Wuzi University, Beijing, China 3School of Information, Beijing Wuzi University, Beijing, China [email protected],[email protected],[email protected] Keywords: university-industry-research collaboration; patent cooperation network; innovation performance Abstract. In university-industry-research collaborative projects, patent cooperation network building and sustaining played an important role, promoting the communication, transfer and share knowledge among universities, scientific research institutions and industry, promoting the effective use of resources, and promoting the improve of innovation ability of colleges and universities. It is worthy of our in-depth discussion what the characteristics and harvest of universities in theuniversity-industry-research collaboration process in Zhejiang, the eastern region more developed on education and economy. Therefore, we select 10 universities in Zhejiang province as the research object, the patent applied by universities and enterprises jointly and applied by universities and research institutions as the starting point to carry on the analysis of cooperation depth, cooperation breadth and network density of the patent cooperation network centering on university in Zhejiang, and further analyze the influence of patent cooperation network in university-industry-research collaboration on innovation performance of colleges and universities empirically through SPSS to make suggestions for universities’ development. Introduction With the knowledge economy era coming, the key role of innovation for a country growing has received wide recognition. -

Delegates Organization Background Beijing Hydrosurvey Science
The 4th China Ocean Technology Conference M ay 16 - 18, 2019, Zhoushan Campus, Zhejiang University D elegates Organization Background Beijing Hydrosurvey Science & Technology Co., Ltd Beijing Institute of Exploration Engineering, MNR Beijing Normal University BGP Inc., China National Petroleum Corporation CETC Chongqing Acoustic - Optic - Electronic Co., Ltd. Chang An University Changshu Ruite Electric Co., Ltd. China Geological Survey China Huarong Ocean Fisheries Development Co., Ltd. China Jiliang University China Oceanic Information Network China University of Geosciences, Beijing China University of Geosciences, Wuhan China University of Petroleum China University of Petroleum (Eastern China) China Academy of Electronics and Information Technology Chinese Institute of Electronics CIMC Ocean Engineering Institute, Zhejiang University CNOOC Research Institute College of Electrical Engineering, Zhejiang University College of Geophysics, China University of Petroleum College of Information Science & Electronic Engineering, Zhejiang University College of Ocean and Earth Sciences, Xiamen University College of Oceanography, Hohai University Dalian University of Technology Department of Physics, Ocean University of China East China Normal University Fudan University Gaungxi University Geological Exploration Technology Institute of Jiangsu Province Guangdong Sea Star Ocean Sci. and Tech. Co., Ltd. Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences Guangzhou Marine Geological Survey Guodian -

Curriculum Vitae
Curriculum Vitae Hong-Kun Xu (徐洪坤) Academic Degree: Ph.D. (April 1988) Academic Rank: Professor Current Position: Distinguished Professor Department of Mathematics, Hangzhou Dianzi University Hangzhou 310018, China Tel: +86 (0)571 86873875 (O); cell: 15356199736 E-mail: [email protected], [email protected] HIGHER EDUCATION B.Sc.: October 1978-July 1982 Department of Mathematics Zhejiang Normal University Jinghua City, Zhejiang Province, mainland China M.Sc.: September 1982-May 1985 Department of Mathematics Zhejiang University Hangzhou City, Zhejiang Province, mainland China Ph.D.: May 1985-May 1988 Department of Mathematics Xi'an Jiaotong University Xi'an City, Shaanxi Province, mainland China EMPLOYMENT Lecturer: May 1985-August 1990 Associate Professor: September 1990-October 1992 Department of Mathematics and Institute for Applied Mathematics East China University of Science and Technology Shanghai, China Visiting Professor: October 1992-July 1993 Departamento de Analisis, Facultad de Matematicas Universidad de Sevilla Sevilla, Spain Postdoctoral Fellow: August 1993-July 1994 Department of Mathematics, Statistics and Computing Science Dalhousie University Halifax, Canada 1 Associate Professor: August 1994-December 1996 Professor: January 1997-March 2003 Senior Professor, April 2003– December 2007 School of Mathematical Sciences University of KwaZulu-Natal Durban, South Africa Professor: February 1999-July 2000 Department of Mathematics College of Science King Saud University Riyadh, Saudi Arabia Chair Professor: January 2008-January 2015 Department of Applied Mathematics National Sun Yat-sen University Kaohsiung, Taiwan Distinguished Professor: February 2015-present Hangzhou Dianzi University Hangzhou, China ADMINISTRATION EXPERIENCE 行政經歷 • Head of the Department of Applied Mathematics, National Sun Yat-sen University (國立中山大學應用數學系系主任),November 1, 2010-July 31, 2013. -

99Mtc-MIBI Positive of Cervical Ectopic Thymoma Case Report and Literature Review
2019 10th International Conference on Information Technology in Medicine and Education (ITME 2019) Qingdao, China 23 – 25 August 2019 IEEE Catalog Number: CFP1953E-POD ISBN: 978-1-7281-3919-7 Copyright © 2019 by the Institute of Electrical and Electronics Engineers, Inc. All Rights Reserved Copyright and Reprint Permissions: Abstracting is permitted with credit to the source. Libraries are permitted to photocopy beyond the limit of U.S. copyright law for private use of patrons those articles in this volume that carry a code at the bottom of the first page, provided the per-copy fee indicated in the code is paid through Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923. For other copying, reprint or republication permission, write to IEEE Copyrights Manager, IEEE Service Center, 445 Hoes Lane, Piscataway, NJ 08854. All rights reserved. *** This is a print representation of what appears in the IEEE Digital Library. Some format issues inherent in the e-media version may also appear in this print version. IEEE Catalog Number: CFP1953E-POD ISBN (Print-On-Demand): 978-1-7281-3919-7 ISBN (Online): 978-1-7281-3918-0 ISSN: 2474-381X Additional Copies of This Publication Are Available From: Curran Associates, Inc 57 Morehouse Lane Red Hook, NY 12571 USA Phone: (845) 758-0400 Fax: (845) 758-2633 E-mail: [email protected] Web: www.proceedings.com 2019 10th International Conference on Information Technology in Medicine and Education (ITME) ITME 2019 Table of Contents Message from the ITME 2019 General Chairs xxiii Message from