DOCSLIB.ORG

Week 8 Solutions Page 1 Exercise (5.1.3). Let F : [A, B]

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Week 8 Solutions Page 1 Exercise (5.1.3). Let F : [A, B] Week 8 Solutions Page 1 Exercise (5.1.3). Let f :[a; b] ! R be a bounded function. Suppose that there exists a sequence of partitions fPkg of [a; b] such that lim (U(Pk; f) − L(Pk; f)) = 0: k!1 Show that f is Riemann integrable and that Z b f = lim U(Pk; f) = lim L(Pk; f): a k!1 k!1 Proof. Given " > 0, by assumption there exists a N 2 N such that when k ≥ N, U(Pk; f) − L(Pk; f) < ". Specifically, U(PN ; f) − L(PN ; f) < ". Then, Z b Z b 0 ≤ f − f ≤ U(PN ; f) − L(PN ; f) < " a a Since " > 0 was arbitrary, we must have Z b Z b Z b Z b f − f = 0 or f = f: a a a a Therefore, f is Riemann integrable. R b Next,we show that f = lim U(Pk; f). Let " > 0 be given. Choose N 2 N a k!1 such that when k ≥ N, U(Pk; f) − L(Pk; f) < ". Then, when k ≥ N Z b Z b U(Pk; f) − f = U(Pk; f) − f a a Z b = U(Pk; f) − f a ≤ U(Pk; f) − L(Pk; f) < . R b Hence, we have that f = lim U(Pk; f). a k!1 Z b Finally, since lim (U(Pk; f) − L(Pk; f)) = 0 and lim U(Pk; f) = f, k!1 k!1 a lim L(Pk; f) = lim [U(P; k) − (U(Pk; f) − L(Pk; f))] k!1 k!1 = lim U(P; k) − lim (U(Pk; f) − L(Pk; f)) k!1 k!1 Z b = f − 0 a Z b = f: a Week 8 Solutions Page 2 Exercise (5.1.6). Let c 2 (a; b) and let d 2 R. Define f :[a; b] ! R as ( d if x = c; f(x) := 0 if x 6= c: R b Prove that f 2 R[a; b] and compute a f using the definition of the integral (and propositions of the section). Proof. Without loss of generality, assume that d > 0. Let " > 0 be given. Let 0 < β < minfc − a; b − c; "=2dg. Let P := fa; c − β; c + β; bg. Then, 3 X U(P; f) − L(P; f) = (Mj − mj)∆xj j=1 = (0 − 0)∆x1 + (d − 0)∆x2 + (0 − 0)∆x3 = d(2β) = 2dβ < ": Therefore, by the Cauchy criterion, f is integrable. Next, for any " > 0, if we define P as above, we have Z b 0 = L(P; f) ≤ f ≤ U(P; f) < ": a R b Since " was arbitrary, this gives that a f = 0. Exercise (5.2.1). Let f be in R[a; b]. Prove that −f is in R[a; b] and Z b Z b −f(x) dx = − f(x) dx: a a Proof. Note that for any set A ⊆ R, sup(−A) = − inf A and inf(−A) = − sup A, where −A = {−a : a 2 Ag. Week 8 Solutions Page 3 Let P = fx0; x1; x2; : : : ; xn−1; xng be any partition of [a; b], and let Ik = [xk−1; xk] denote the kth subinterval created by the partition. Then, using the above fact, we have that for k = 1; : : : ; n, n X U(P; −f) = sup(−f(x))∆xk I k=1 k n X = − inf f(x)∆xk Ik k=1 n X = − inf f(x)∆xk Ik k=1 = −L(P; f) Similarly, L(P; −f) = −U(P; f). Hence, U(P; −f) − L(P; −f) = −L(P; f) − (−U(P; f)) = U(P; f) − L(P; f) Since f is integrable, from problem 5.1.3, there is a sequence of partitions (Pk)k2N such that limk!1(U(Pk; f) − L(Pk; f)) = 0. Then, for the same se- quence, lim (U(Pk; −f) − L(Pk; −f)) = lim (U(Pk; f) − L(Pk; f)) = 0 k!1 k!1 and so −f is integrable if and only if f is integrable. Finally, since f and −f are both integrable we have that Z b Z b −f(x) dx = − f(x) dx a a = supfL(P; −f): P is a partition of [a; b]g = sup{−U(P; f): P is a partition of [a; b]g = − inffU(P; f): P is a partition of [a; b]g Z b = − f(x) dx a Z b = − f(x) dx: a Week 8 Solutions Page 4 Exercise (5.2.4). Prove the mean value theorem for integrals. That is, prove that if f :[a; b] ! R is continuous, then there exists a c 2 [a; b] such that R b a f = f(c)(b − a). Proof. By the Min-Max Theorem, f achieves both an absolute maximum M and an absolute minimum m in [a; b], say at points c1 and c2. Without loss of generality, c1 < c2. Then we have that Z b m(b − a) ≤ f ≤ M(b − a): a or 1 Z b m ≤ f ≤ M: (b − a) a By the Intermediate Value Theorem, there must be a point c 2 (c1; c2) ⊂ [a; b] such that 1 Z b f(c) = f: (b − a) a Therefore, for this c, Z b f = f(c)(b − a): a R b Exercise (5.2.6). Suppose f :[a; b] ! R is a continuous function and a f = 0. Prove that there exists a c 2 [a; b] such that f(c) = 0. R b Proof. Apply Exercise 5.2.4 with a f = 0 to obtain the conclusion..
Load more

Recommended publications
  • F(P,Q) = Ffeic(R+TQ)
    674 MATHEMA TICS: N. H. McCOY PR.OC. N. A. S. ON THE FUNCTION IN QUANTUM MECHANICS WHICH CORRESPONDS TO A GIVEN FUNCTION IN CLASSICAL MECHANICS By NEAL H. MCCoy DEPARTMENT OF MATHEMATICS, SMrTH COLLEGE Communicated October 11, 1932 Let f(p,q) denote a function of the canonical variables p,q of classical mechanics. In making the transition to quantum mechanics, the variables p,q are represented by Hermitian operators P,Q which, satisfy the com- mutation rule PQ- Qp = 'y1 (1) where Y = h/2ri and 1 indicates the unit operator. From group theoretic considerations, Weyll has obtained the following general rule for carrying a function over from classical to quantum mechanics. Express f(p,q) as a Fourier integral, f(p,q) = f feiC(r+TQ) r(,r)d(rdT (2) (or in any other way as a linear combination of the functions eW(ffP+T)). Then the function F(P,Q) in quantum mechanics which corresponds to f(p,q) is given by F(P,Q)- ff ei(0P+7Q) t(cr,r)dodr. (3) It is the purpose of this note to obtain an explicit expression for F(P,Q), and although we confine our statements to the case in which f(p,q) is a polynomial, the results remain formally correct for infinite series. Any polynomial G(P,Q) may, by means of relation (1), be written in a form in which all of the Q-factors occur on the left in each term. This form of the function G(P,Q) will be denoted by GQ(P,Q).
    [Show full text]
  • THE ZEROS of QUASI-ANALYTIC FUNCTIONS1 (3) H(V) = — F U-2 Log
    THE ZEROS OF QUASI-ANALYTICFUNCTIONS1 ARTHUR O. GARDER, JR. 1. Statement of the theorem. Definition 1. C(Mn, k) is the class of functions f(x) ior which there exist positive constants A and k and a sequence (Af„)"_0 such that (1) |/(n)(x)| ^AknM„, - oo < x< oo,» = 0,l,2, • • • . Definition 2. C(Mn, k) is a quasi-analytic class if 0 is the only element / of C(Mn, k) ior which there exists a point x0 at which /<">(*„)=0 for « = 0, 1, 2, ••• . We introduce the functions (2) T(u) = max u"(M„)_l, 0 ^ m < oo, and (3) H(v) = — f u-2 log T(u)du. T J l The following property of H(v) characterizes quasi-analytic classes. Theorem 3 [5, 78 ].2 Let lim,,.,*, M„/n= °o.A necessary and sufficient condition that C(Mn, k) be a quasi-analytic class is that (4) lim H(v) = oo, where H(v) is defined by (2) and (3). Definition 4. Let v(x) be a function satisfying (i) v(x) is continuously differentiable for 0^x< oo, (ii) v(0) = l, v'(x)^0, 0^x<oo, (iii) xv'(x)/v(x)=0 (log x)-1, x—>oo. We shall say that/(x)GC* if and only if f(x)EC(Ml, k), where M* = n\[v(n)]n and v(n) satisfies the above conditions. Definition 5. Let Z(u) be a real-valued function which is less Received by the editors November 29, 1954 and, in revised form, February 24, 1955. 1 Presented to the Graduate School of Washington University in partial fulfill- ment of the requirements for the degree of Doctor of Philosophy.
    [Show full text]
  • CONDITIONAL EXPECTATION Definition 1. Let (Ω,F,P)
    CONDITIONAL EXPECTATION 1. CONDITIONAL EXPECTATION: L2 THEORY ¡ Definition 1. Let (­,F ,P) be a probability space and let G be a σ algebra contained in F . For ¡ any real random variable X L2(­,F ,P), define E(X G ) to be the orthogonal projection of X 2 j onto the closed subspace L2(­,G ,P). This definition may seem a bit strange at first, as it seems not to have any connection with the naive definition of conditional probability that you may have learned in elementary prob- ability. However, there is a compelling rationale for Definition 1: the orthogonal projection E(X G ) minimizes the expected squared difference E(X Y )2 among all random variables Y j ¡ 2 L2(­,G ,P), so in a sense it is the best predictor of X based on the information in G . It may be helpful to consider the special case where the σ algebra G is generated by a single random ¡ variable Y , i.e., G σ(Y ). In this case, every G measurable random variable is a Borel function Æ ¡ of Y (exercise!), so E(X G ) is the unique Borel function h(Y ) (up to sets of probability zero) that j minimizes E(X h(Y ))2. The following exercise indicates that the special case where G σ(Y ) ¡ Æ for some real-valued random variable Y is in fact very general. Exercise 1. Show that if G is countably generated (that is, there is some countable collection of set B G such that G is the smallest σ algebra containing all of the sets B ) then there is a j 2 ¡ j G measurable real random variable Y such that G σ(Y ).
    [Show full text]
  • ARIC Surveillance Variable Dictionary Incident Stroke
    ARIC Surveillance Variable Dictionary Incident Stroke April 2002 j:\aric\admin\vardict\stroke_inc ARIC Surveillance Variable Dictionary – Incidenta Stroke Table of Contents for Year YYb Alphabetical Index .....................................................................................................................................ii 1. Classification Variable COMPDIAG (Computer Diagnosis) ............................................................................................... 1 COMP_DX (Computer Diagnosis – Format Value) ....................................................................... 2 FINALDX (Final Diagnosis) .......................................................................................................... 3 FINAL_DX (Final Diagnosis – Format Value) .............................................................................. 4 2. Event Time/Type & Eligibility Variable DISDATE (Discharge/Death Date) ................................................................................................5 EVENTYPE (Event Type) .............................................................................................................. 6 YEAR (Event Year) ........................................................................................................................ 7 SK_ELIG2 (Stoke Eligibility) ........................................................................................................ 8 3. Incidence* Stroke Variable 3.1 Incident Event CENSORYY (Censoring Date) .....................................................................................................
    [Show full text]
  • Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone
    Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Table of Contents 1. General Information 2 1.1 Use of Latin Script characters in domain names 3 1.2 Target Script for the Proposed Generation Panel 4 1.2.1 Diacritics 5 1.3 Countries with significant user communities using Latin script 6 2. Proposed Initial Composition of the Panel and Relationship with Past Work or Working Groups 7 3. Work Plan 13 3.1 Suggested Timeline with Significant Milestones 13 3.2 Sources for funding travel and logistics 16 3.3 Need for ICANN provided advisors 17 4. References 17 1 Generation Panel for Latin Script Label Generation Ruleset for the Root Zone 1. General Information The Latin script1 or Roman script is a major writing system of the world today, and the most widely used in terms of number of languages and number of speakers, with circa 70% of the world’s readers and writers making use of this script2 (Wikipedia). Historically, it is derived from the Greek alphabet, as is the Cyrillic script. The Greek alphabet is in turn derived from the Phoenician alphabet which dates to the mid-11th century BC and is itself based on older scripts. This explains why Latin, Cyrillic and Greek share some letters, which may become relevant to the ruleset in the form of cross-script variants. The Latin alphabet itself originated in Italy in the 7th Century BC. The original alphabet contained 21 upper case only letters: A, B, C, D, E, F, Z, H, I, K, L, M, N, O, P, Q, R, S, T, V and X.
    [Show full text]
  • Makes Sense Only If P(E) = 0. Discrete Distribution Function: M(Ω)
    Math 161 0 - Probability, Fall Semester 2012-2013 Dan Abramovich Conditional probabilities P (F jE) := P (F \ E)=P (E). Makes sense only if P (E) =6 0. Discrete distribution function: m(!) = P (f!g), so 8m(!) < ! 2 E m(!jE) := P (E) :0 ! 62 E: The effect is to replace Ω by E! Continuous: 8 f(!) < ! 2 E f(!jE) := P (E) :0 ! 62 E: 1 2 Example 1: cast a die. E = f! ≥ 4g, F = f! = 6g. P (F jE) = (1=6)=(1=2) = 1=3: P (EjF ) = 1. Example 2: two urns, 2B+3W, 1B+1W P (IjB) =? (2=10)=(2=10 + 1=4) \Bayes probabilities" 3 Example: Monty Hall problem. Say player chooses door 1 always (see book for removing this) draw table 13: 1/6; 12:1/6 23: 1/3 32: 1/6 P (C =6 1jM = 3) = (1=3)=(1=3 + 1=6) = 2=3. cgG 1/6 cGg 1/6 gcG 1/3 gCg 0 ggC 0 gGc 1/3 4 independent events P (F jE) = P (F ) Claim: if nonzero, implies P (F jE) = P (F ) Proof: the definition says P (F jE) = P (E \F )=P (E) so P (F jE)P (E) = P (E \ F ): Now P (EjF ) = P (E\F )=P (F ) = P (F jE)P (E)=P (F ) = P (E) by as- sumption. Can do the same for a collection of events: Ai are independent if P (Ai1∩· · ·∩Aik) = P (Ai1) ··· P (Aik) for distinct ij. Example: A1 first coin heads, A2 second coin heads, B =even number of heads.
    [Show full text]
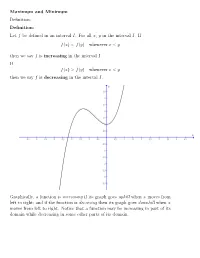
  • Maximum and Minimum Definition
    Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing.
    [Show full text]
  • The Alphabets of the Bible: Latin and English John Carder
    274 The Testimony, July 2004 The alphabets of the Bible: Latin and English John Carder N A PREVIOUS article we looked at the trans- • The first major change is in the third letter, formation of the Hebrew aleph-bet into the originally the Hebrew gimal and then the IGreek alphabet (Apr. 2004, p. 130). In turn Greek gamma. The Etruscan language had no the Greek was used as a basis for writing down G sound, so they changed that place in the many other languages. Always the spoken lan- alphabet to a K sound. guage came first and writing later. We complete The Greek symbol was rotated slightly our look at the alphabets of the Bible by briefly by the Romans and then rounded, like the B considering Latin, then our English alphabet in and D symbols. It became the Latin letter C which we normally read the Bible. and, incidentally, created the confusion which still exists in English. Our C can have a hard From Greek to Latin ‘k’ sound, as in ‘cold’, or a soft sound, as in The Greek alphabet spread to the Romans from ‘city’. the Greek colonies on the coast of Italy, espe- • In the sixth place, either the Etruscans or the cially Naples and district. (Naples, ‘Napoli’ in Romans revived the old Greek symbol di- Italian, is from the Greek ‘Neapolis’, meaning gamma, which had been dropped as a letter ‘new city’). There is evidence that the Etruscans but retained as a numeral. They gave it an ‘f’ were also involved in an intermediate stage.
    [Show full text]
  • Fonts for Latin Paleography 
    FONTS FOR LATIN PALEOGRAPHY Capitalis elegans, capitalis rustica, uncialis, semiuncialis, antiqua cursiva romana, merovingia, insularis majuscula, insularis minuscula, visigothica, beneventana, carolina minuscula, gothica rotunda, gothica textura prescissa, gothica textura quadrata, gothica cursiva, gothica bastarda, humanistica. User's manual 5th edition 2 January 2017 Juan-José Marcos [email protected] Professor of Classics. Plasencia. (Cáceres). Spain. Designer of fonts for ancient scripts and linguistics ALPHABETUM Unicode font http://guindo.pntic.mec.es/jmag0042/alphabet.html PALEOGRAPHIC fonts http://guindo.pntic.mec.es/jmag0042/palefont.html TABLE OF CONTENTS CHAPTER Page Table of contents 2 Introduction 3 Epigraphy and Paleography 3 The Roman majuscule book-hand 4 Square Capitals ( capitalis elegans ) 5 Rustic Capitals ( capitalis rustica ) 8 Uncial script ( uncialis ) 10 Old Roman cursive ( antiqua cursiva romana ) 13 New Roman cursive ( nova cursiva romana ) 16 Half-uncial or Semi-uncial (semiuncialis ) 19 Post-Roman scripts or national hands 22 Germanic script ( scriptura germanica ) 23 Merovingian minuscule ( merovingia , luxoviensis minuscula ) 24 Visigothic minuscule ( visigothica ) 27 Lombardic and Beneventan scripts ( beneventana ) 30 Insular scripts 33 Insular Half-uncial or Insular majuscule ( insularis majuscula ) 33 Insular minuscule or pointed hand ( insularis minuscula ) 38 Caroline minuscule ( carolingia minuscula ) 45 Gothic script ( gothica prescissa , quadrata , rotunda , cursiva , bastarda ) 51 Humanist writing ( humanistica antiqua ) 77 Epilogue 80 Bibliography and resources in the internet 81 Price of the paleographic set of fonts 82 Paleographic fonts for Latin script 2 Juan-José Marcos: [email protected] INTRODUCTION The following pages will give you short descriptions and visual examples of Latin lettering which can be imitated through my package of "Paleographic fonts", closely based on historical models, and specifically designed to reproduce digitally the main Latin handwritings used from the 3 rd to the 15 th century.
    [Show full text]
  • A Little Flourish Pattern B
    APQ APRIL 2015 CMR Modern Lace Pillow Full-Size Patterns C. Neubauer 10-29-14 100547567 A Little Flourish Pattern B A Little Flourish Pattern A APQ APRIL 2015 CMR Modern Lace Pillow APQ APRIL 2015 Full-Size Patterns CMR C. Neubauer 10-29-14 Modern Lace Pillow 100547567 Full-Size Patterns APQ APRIL 2015 C. Neubauer 10-29-14 A Little APQ APRIL 2015 A LittleFlourish Flourish CMR 100547567 Pattern N Modern Lace Pillow CMR Pattern B A Little Full-Size Patterns Modern Lace Pillow Flourish APQ APRIL 2015 Full-Size Patterns C. Neubauer 10-29-14 CMR Pattern B A Little Flourish 100547567 C. Neubauer 10-29-14 Pattern A Modern Lace Pillow 100547567 A Little Full-Size Patterns A Little A Little Flourish C. Neubauer 10-29-14 Flourish Pattern A Pattern B Flourish 100547567 Pattern B APQ APRILA 2015 Little A Little A Little Flourish CMR Flourish Flourish A Little Flourish Pattern B Pattern A A Little Flourish Modern Lace Pillow Pattern E Pattern A Pattern I Full-Size Patterns A Little Flourish A Little C. Neubauer 10-29-14APQ APRIL 2015 100547567 CMR A Little Flourish Pattern A Flourish American Patchwork & Quilting | Quilt Sampler | Quilts and More Pattern C A Little Pattern M Modern Lace Pillow APQ APRIL 2015 Full-Size Patterns CMR Flourish C. Neubauer 10-29-14 Pattern B Modern Lace Pillow Project: A Little Flourish100547567 Full-Size Patterns A Little A Little Flourish APQ APRIL 2015C. Neubauer 10-29-14 Flourish Pattern A CMR 100547567 Pattern B A Little Flourish Modern Lace Pillow Pattern N A ALittle Little FlourishFlourish Full-Size Patterns A Little Flourish C.
    [Show full text]
  • Komi Latin Letters Missing in Unicode 2
    WG2 N5101 ISO/IEC JTC 1/SC 2/WG 2 PROPOSAL SUMMARY FORM TO ACCOMPANY SUBMISSIONS 1 FOR ADDITIONS TO THE REPERTOIRE OF ISO/IEC 10646TP PT Please fill all the sections A, B and C below. Please read Principles and Procedures Document (P & P) from HTU http://std.dkuug.dk/JTC1/SC2/WG2/docs/principles.html UTH for guidelines and details before filling this form. Please ensure you are using the latest Form from HTU http://std.dkuug.dk/JTC1/SC2/WG2/docs/summaryform.htmlUTH. See also HTU http://std.dkuug.dk/JTC1/SC2/WG2/docs/roadmaps.html UTH for latest Roadmaps. A. AdministratiVe 1. Title: Komi Latin letters missing in Unicode 2. Requester's name: Jack Michael Rueter 3. Requester type (Member body/Liaison/Individual Member body contribution): 4. Submission date: 2019-04-24 5. Requester's reference (if applicable): 6. Choose one of the following: This is a complete proposal: YES (or) More information will be provided later: NO B. Technical – General 1. Choose one of the following: a. This proposal is for a new script (set of characters): NO Proposed name of script: b. The proposal is for addition of character(s) to an existing block: YES Name of the existing block: Latin Extensions 2. Number of characters in proposal: 16 3. Proposed category (select one from below - see section 2.2 of P&P document): A-Contemporary B.1-Specialized (small collection) B.2-Specialized (large collection) X C-Major extinct D-Attested extinct E-Minor extinct F-Archaic Hieroglyphic or Ideographic G-Obscure or questionable usage symbols 4.
    [Show full text]
  • Issues Related to Non-Latin Characters in Name Authority Records
    WHITE PAPER : ISSUES RELATED TO NON-LATIN CHARACTERS IN NAME AUTHORITY RECORDS Non-Latin Characters in Name Authority Records The major authority record exchange partners (British Library, Library and Archives Canada, Library of Congress, National Library of Medicine, OCLC, and RLG Programs (and predecessors)) have agreed to a basic outline that will allow for the addition of non-Latin characters in references on name authority records distributed as part of the NACO program—no earlier than April 2008. Rather than using 880 fields that parallel ‘regular’ MARC fields as in bibliographic records, non-Latin script references in authorities will be added following MARC 21’s “Model B” for multi-script records. Model B provides for unlinked non-Latin script fields with the same MARC tags used for romanized data, such as authority record 4XX fields. Although there was initial discussion about choosing a ‘preferred’ non- Latin script variant form and flagging it as such on the authority record, it was recognized that forging agreements about what constituted the ‘preferred’ form could seriously delay the addition of non-Latin references. The group preferred a plan with a short-term goal to allow non-Latin references without declaring whether that reference was the preferred form for any particular language or script. As references are allowed to conflict, no attempt is needed to determine if non-Latin references on one record normalize to the same form as other non-Latin references on different records. Pre-Population of the LC/NACO Authority File While the record-by-record addition of non-Latin references to new or existing authority records will be optional for NACO participants, OCLC has proposed to pre-populate the LC/NACO Authority File with non-Latin references derived from non-Latin bibliographic heading fields from WorldCat, making use of data-mining techniques developed for the WorldCat Identities product.
    [Show full text]