DOCSLIB.ORG

WHY MULTIVARIATE ANALYSIS? • Used for Analysing Complicated

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
WHY MULTIVARIATE ANALYSIS? • Used for Analysing Complicated WHY MULTIVARIATE ANALYSIS? • Used for analysing complicated data sets • When there are many Independent Variables (IVs) and/or many Dependent Variables (DVs) • When IVs and DVs are correlated with one Dr. Azmi Mohd Tamil another to varying degrees Jabatan Kesihatan Masyarakat Fakulti Perubatan UKM • When need to come up with Prediction Model Based on lecture notes by Dr Azidah Hashim • Parallels greater complexity of contemporary research USING MULTIVARIATE ANALYSIS CHOICE OF APPROPRIATE STATISTICAL METHOD BASED ON: • WHICH STATISTICAL PROCEDURE TO USE? • Nature of IVs and DVs • HOW TO PERFORM CHOSEN PROCEDURE? • Investigator’s Experience • Personal Preferences • HOW TO INFER FROM RESULTS OBTAINED? • Ease of Comfort with Methods Used • Literature Review References • ANY OTHER ALTERNATIVE APPROACH? • Consultation with Statistician BASIC PREMISE I: BASIC PREMISE I: TERM USED:- Relationship between X Y X Y Independent Variable (IV) Dependent Variable (DV) Predictor Outcome Explanatory Response Eg . Smoking Lung Cancer Risk Factor Effect Age Hypertension Covariates (Continuous) Maternal ANC Birthweight Factor (Categorical) Control INDEPENDENT DEPENDENT VARIABLE VARIABLE Confounders RISK FACTOR OUTCOME Nuisance 1 BASIC PREMISE II: TERMINOLOGY: Univariate Analysis DATA • Analysis in which there is a single DV Bivariate Analysis Qualitative Quantitative • Analysis of two variables (categorical) • Wish to simply study the relationship between -Dichotomous -Continuous the variables - Polynomial -Discrete Multivariate Analysis • Simultaneously analyse multiple DVs and IVs Rough Guide to Multivariate BASIC PREMISE 111:VARIATIONS OF Methods (1) THE SAME THEME Name Xs Y THE GENERAL LINEAR MODEL: Regression and Continuous Continuous Correlation (eg. age) (eg. BP) Y = a + b1x1 + b2x2 + b3x3 …. + bixi Analysis of Variance Categorical Continuous Used in the following procedures: (ANOVA) (eg. SES) (eg. BP) ANOVA Analysis of Categorical Continuous ANCOVA Covariance and Continuous (eg BP) Multiple Linear Regression (ANCOVA) (eg age and SES) Multiple Logistic Regression Log Linear Regression Discriminant Function Rough Guide to Multivariate Methods (2) BASIC PREMISE IV: Name Xs Y Multiple Linear Continuous Continuous Regression (eg. Age, Ht, (eg. BP) Wt) TWO APPROACHES TO CHOOSING: Logistic Regression Continuous Categorical (eg. age) (eg. CHD) 1. Based on Type of Modelling Logistic Regression Categorical Categorical (eg. sex) (eg. CHD) 2. Based on Type of Research Question Discriminant Continuous Nominal / Function Analysis (eg. Age, Ordinal Income) (eg. Quality of Life) 2 MODELLING: TWO TYPES OF MODELLING TOOLS: Prior Knowledge Discovery 1. Theory Driven-Hypothesis Testing: Attempts to substantiate or disprove preconceived ideas Model 2. Data Driven: Building Validation Deployment Automatically creates model based on patterns found in data THEORY-DRIVEN MODELLING TOOLS: DATA-DRIVEN MODELLING TOOLS: CORRELATIONS CLUSTER ANALYSIS t-TESTS FACTOR ANALYSIS ANOVA DECISION TREES LINEAR REGRESSION DATA VISUALISATION LOGISTIC REGRESSION NEURAL NETWORKS DISCRIMINANT ANALYSIS FORECASTING METHODS BASIC PREMISE IV: RESEARCH QUESTION I: Degree of Relationship among Variables Types of Research Questions Statistical technique: • Degree of Relationship among a. Bivariate r (Bivariate correlation and Variables Regression) • Significance of Group Differences b. Multiple R ( Multiple Correlation and Multiple Regression) • Prediction of Group Membership c. Sequential R • Structure d. Canonical R e. Multiway Frequency Analysis 3 RESEARCH QUESTION II: RESEARCH QUESTION III Significance of Group Differences Prediction of Group Membership Statistical Techniques: Statistical technique a. t-test b. One-way ANOVA c. Two-way ANOVA a. Discriminant Function d. Profile Analysis b. Multiway Frequency Analysis (Logit) c. Logistic Regression PRELIMINARY CHECK OF DATA RESEARCH QUESTION IV BEFORE MULTIVARIATE ANALYSIS Structure • Accuracy of Data File • Honest Correlation • Missing Data Statistical technique: •Outliers a. Principal Component Analysis • Normality, linearity and homoscedasticity Regression b. Factor Analysis • Multicollinearity and Singularity Diagnostics c. Structural Equation Modelling • Common Data Transformations Univariate outliers ACCURACY OF DATA FILE : 600 Inspect univariate descriptive statistics for accuracy of input 500 73 a. Out-of-range values 400 b. Plausible means and standard deviation 300 c. Coefficient of variation d. Univariate outliers 200 100 141198211181 0 N = 184 Pre-pregnancy weight 4 Inflated Correlation HONEST CORRELATIONS • If composite variables are to be used and • Inflated Correlation two or more composite variables have the • Deflated Correlation same raw data, correlation can be inflated. • Inaccurately Completed • i.e. correlation between BMI and weight Deflated Correlation Inaccurately Completed 1) the range of values for one variable is restricted; “relationship between annual average daily traffic count • Questionnaires inaccurately completed due (AADT) and accidents on rural highways and picks a remote region where all AADT's are less than 3000, then to lack of time, lack of concern, emotional if there is a good correlation, he is likely to bias will affect correlation. underestimate it with such a restricted range on one variable. 2) if an intervening variable mediates between two variables; “relationship between thickness of asphalt and chloride content, then picking only those bridges in the population which have a waterproofing membrane will likely push down the estimate. The waterproofing membrane intervenes, literally and statistically. ” MISSING DATA MISSING DATA How to handle missing data a. Deleting cases or variables Seriousness depends on Random b. Estimating missing data • Pattern of missing data Non-Random - use of prior knowledge • How much is missing - inserting mean values • Why is it missing - using regression c. Using a missing data correlation matrix d. Treating missing data as data e. Repeating analyses with and without missing data 5 OUTLIERS • Cases with such extreme values on one OUTLIERS : variable or a combination of variables that they distort statistics • Presence due to Measure of Impact : Leverage - incorrect data entry Discrepancy - failure to specify missing value codes Influence - outlier is not a member of target population - distribution for variable in population is more skewed than normal The relationship among leverage, discrepancy and influence x OUTLIERS : x Dealing with Outliers High leverage, low discrepancy, High leverage, high discrepancy, • Find and remedy errors in data entry moderate influence high influence • Find and remedy missing values specification • Deletion • Retention with alteration x Low leverage, high discrepancy, moderate influence NORMALITY, LINEARITY AND OUTLIERS : HOMOSCEDASCITY Detecting Outliers Need for Multivariate Normality Univariate outliers: - assumption that each variable and all linear - inspection of z-scores combinations of the variables are normally distributed - graphical methods e.g. histograms, box plots, normal probability plots - robustness to violation of assumption still inconclusive Multivariate outliers: - computation of Mahalanobis distance 6 NORMALITY Normal - assessed via statistical or graphical methods - 2 components: skewness and kurtosis - if non-normal, consider transformation Positive skewness Negative skewness Positive kurtosis Negative kurtosis Predicted Y’ Predicted Y’ Curvilinear Relationship ) s r Assumptions o r Failure of r e Met ( Normality s l a u d i s e R (a) (b) Number of symptoms of Number Number of symptoms of Number ) Low Moderate High Low Moderate High s r o r r DOSAGE DOSAGE e Heteroscedasticity Non- ( s Linearity l a (a) Curvilinear (a) Curvilinear + linear u d i s e R (c) (d) HOMOSCEDASTICITY LINEARITY - assumption that the variability in scores for one continuous variable is roughly the - assumption of a straight line relationship same at all values of another continuous between 2 variables variable - Nonlinearity is diagnosed from -failure due to • residuals plots or • non normality of one of the variables or • bivariate scatterplots • one variable is related to some transformation of the other 7 COLLINEARITY PRESENCE OF COLLINEARITY CAUSES - concerns the relationship of the IVs to one another and does not directly - Unstable regression coefficient estimates involve the response variable - Large estimates of coefficient variances eg. - Wide 95% Confidence Limits Physical Activity Blood -Large p-values Collinearity Pressure - Large Standard errors Age MULTICOLLINEARITY AND PROBLEMS WITH MULTICOLLINEARITY SINGULARITY AND SINGULARITY (related to a Correlation Matrix) Multicollinearity : Variables are too highly correlated (> 0.90) - inflate size of error - weaken analysis Singularity : Variables are redundant; Matrix cannot be inversed the variables are perfectly correlated. expose the redundancy of variables and the need to remove variables from the analysis. TYPES OF TRANSFORMATIONS COMMON DATA TRANSFORMATION Square root Logarithm Inverse • recommended as a remedy for outliers and for failures of normality, linearity and homoscedasticity Reflect and square Reflect and logarithm Reflect and inverse root 8 MULTIVARIATE RELATIONSHIP APPLICATIONS OF MULTIVARIATE ANALYSIS X a) The primary purpose is to study the effect on eg. age variable Y of changes in a particular single variable Y X1, but it is recognised that Y may be affected by several other variables X,X, … The effect on Y of eg. CHD X simultaneous changes in
Load more

Recommended publications
  • T-TEST Outline Hypothesis Testing Steps Bivariate Analysis
    Bivariate Analysis T-TEST Variable 1 2 LEVELS >2 LEVELS CONTINUOUS Variable 2 2 LEVELS X2 X2 t-test chi square test chi square test >2 LEVELS X2 X2 ANOVA chi square test chi square test (F-test) CONTINUOUS t-test ANOVA -Correlation (F-test) -Simple linear Regression Outline Comparison of means: t-test Hypothesis testing steps T-test is used when one variable is of a continuous nature and the other is dichotomous. T-test The t-test is used to compare the means of two groups on a given variable. Anova Examples: Difference in average blood pressure among males & females. Difference in average BMI among those who exercise and those who do not. Hypothesis testing steps Comparison of means: t-test Example 1: Identify the study objective Research question: Among university students, is there a State the null & alternative hypothesis difference between the average weight for males versus females? Select the proper test statistic Null hypothesis (Ho): μ weight males = μ weight females Calculate the test statistic Alternative hypothesis (Ha): μ weight males ≠ μ weight females Take a statistical decision based on the p-value. Statistical test: t-test Reject or accept the null hypothesis Comparison of means: t-test Comparison of means: t-test T-Test (SPSS output) If this p-value is < 0.05 then reject null hypothesis and conclude that the variances are different (accept alternative) Group Statistics and hence check this p-value for the t-test. Std. Error gender N Mean Std. Deviation Mean weight male 804 75.92 12.843 .453 If this p-value is > 0.05 then accept null hypothesis and female 1135 56.47 8.923 .265 conclude that the variances are equal and hence check this p-value for the t-test.
    [Show full text]
  • Chapter Five Multivariate Statistics
    Chapter Five Multivariate Statistics Jorge Luis Romeu IIT Research Institute Rome, NY 13440 April 23, 1999 Introduction In this chapter we treat the multivariate analysis problem, which occurs when there is more than one piece of information from each subject, and present and discuss several materials analysis real data sets. We first discuss several statistical procedures for the bivariate case: contingency tables, covariance, correlation and linear regression. They occur when both variables are either qualitative or quantitative: Then, we discuss the case when one variable is qualitative and the other quantitative, via the one way ANOVA. We then overview the general multivariate regression problem. Finally, the non-parametric case for comparison of several groups is discussed. We emphasize the assessment of all model assumptions, prior to model acceptance and use and we present some methods of detection and correction of several types of assumption violation problems. The Case of Bivariate Data Up to now, we have dealt with data sets where each observation consists of a single measurement (e.g. each observation consists of a tensile strength measurement). These are called univariate observations and the related statistical problem is known as univariate analysis. In many cases, however, each observation yields more than one piece of information (e.g. tensile strength, material thickness, surface damage). These are called multivariate observations and the statistical problem is now called multivariate analysis. Multivariate analysis is of great importance and can help us enhance our data analysis in several ways. For, coming from the same subject, multivariate measurements are often associated with each other. If we are able to model this association then we can take advantage of the situation to obtain one from the other.
    [Show full text]
  • Package 'Biwavelet'
    Package ‘biwavelet’ May 26, 2021 Type Package Title Conduct Univariate and Bivariate Wavelet Analyses Version 0.20.21 Date 2021-05-24 Author Tarik C. Gouhier, Aslak Grinsted, Viliam Simko Maintainer Tarik C. Gouhier <[email protected]> Description This is a port of the WTC MATLAB package written by Aslak Grinsted and the wavelet program written by Christopher Torrence and Gibert P. Compo. This package can be used to perform univariate and bivariate (cross-wavelet, wavelet coherence, wavelet clustering) analyses. License GPL (>= 2) URL https://github.com/tgouhier/biwavelet BugReports https://github.com/tgouhier/biwavelet/issues LazyData yes LinkingTo Rcpp Imports fields, foreach, Rcpp (>= 0.12.2) Suggests testthat, knitr, rmarkdown, devtools RoxygenNote 7.1.1 NeedsCompilation yes Repository CRAN Date/Publication 2021-05-26 05:10:10 UTC R topics documented: biwavelet-package . .2 ar1.spectrum . .4 ar1_ma0_sim . .5 arrow ............................................6 arrow2 . .7 1 2 biwavelet-package check.data . .7 check.datum . .8 convolve2D . .9 convolve2D_typeopen . 10 enviro.data . 10 get_minroots . 11 MOTHERS . 12 phase.plot . 12 plot.biwavelet . 13 pwtc............................................. 17 rcpp_row_quantile . 19 rcpp_wt_bases_dog . 20 rcpp_wt_bases_morlet . 21 rcpp_wt_bases_paul . 22 smooth.wavelet . 23 wclust . 24 wdist . 25 wt.............................................. 26 wt.bases . 28 wt.bases.dog . 29 wt.bases.morlet . 29 wt.bases.paul . 30 wt.sig . 31 wtc.............................................. 32 wtc.sig . 34 wtc_sig_parallel . 36 xwt ............................................. 37 Index 40 biwavelet-package Conduct Univariate and Bivariate Wavelet Analyses Description This is a port of the WTC MATLAB package written by Aslak Grinsted and the wavelet program written by Christopher Torrence and Gibert P. Compo. This package can be used to perform uni- variate and bivariate (cross-wavelet, wavelet coherence, wavelet clustering) wavelet analyses.
    [Show full text]
  • Meta4diag: Bayesian Bivariate Meta-Analysis of Diagnostic Test Studies for Routine Practice
    meta4diag: Bayesian Bivariate Meta-analysis of Diagnostic Test Studies for Routine Practice J. Guo and A. Riebler Department of Mathematical Sciences, Norwegian University of Science and Technology, Trondheim, PO 7491, Norway. July 8, 2016 Abstract This paper introduces the R package meta4diag for implementing Bayesian bivariate meta-analyses of diagnostic test studies. Our package meta4diag is a purpose-built front end of the R package INLA. While INLA offers full Bayesian inference for the large set of latent Gaussian models using integrated nested Laplace approximations, meta4diag extracts the features needed for bivariate meta-analysis and presents them in an intuitive way. It allows the user a straightforward model- specification and offers user-specific prior distributions. Further, the newly proposed penalised complexity prior framework is supported, which builds on prior intuitions about the behaviours of the variance and correlation parameters. Accurate posterior marginal distributions for sensitivity and specificity as well as all hyperparameters, and covariates are directly obtained without Markov chain Monte Carlo sampling. Further, univariate estimates of interest, such as odds ratios, as well as the SROC curve and other common graphics are directly available for interpretation. An in- teractive graphical user interface provides the user with the full functionality of the package without requiring any R programming. The package is available through CRAN https://cran.r-project.org/web/packages/meta4diag/ and its usage will be illustrated using three real data examples. arXiv:1512.06220v2 [stat.AP] 7 Jul 2016 1 1 Introduction A meta-analysis summarises the results from multiple studies with the purpose of finding a general trend across the studies.
    [Show full text]
  • Correlation and Regression Analysis
    OIC ACCREDITATION CERTIFICATION PROGRAMME FOR OFFICIAL STATISTICS Correlation and Regression Analysis TEXTBOOK ORGANISATION OF ISLAMIC COOPERATION STATISTICAL ECONOMIC AND SOCIAL RESEARCH AND TRAINING CENTRE FOR ISLAMIC COUNTRIES OIC ACCREDITATION CERTIFICATION PROGRAMME FOR OFFICIAL STATISTICS Correlation and Regression Analysis TEXTBOOK {{Dr. Mohamed Ahmed Zaid}} ORGANISATION OF ISLAMIC COOPERATION STATISTICAL ECONOMIC AND SOCIAL RESEARCH AND TRAINING CENTRE FOR ISLAMIC COUNTRIES © 2015 The Statistical, Economic and Social Research and Training Centre for Islamic Countries (SESRIC) Kudüs Cad. No: 9, Diplomatik Site, 06450 Oran, Ankara – Turkey Telephone +90 – 312 – 468 6172 Internet www.sesric.org E-mail [email protected] The material presented in this publication is copyrighted. The authors give the permission to view, copy download, and print the material presented that these materials are not going to be reused, on whatsoever condition, for commercial purposes. For permission to reproduce or reprint any part of this publication, please send a request with complete information to the Publication Department of SESRIC. All queries on rights and licenses should be addressed to the Statistics Department, SESRIC, at the aforementioned address. DISCLAIMER: Any views or opinions presented in this document are solely those of the author(s) and do not reflect the views of SESRIC. ISBN: xxx-xxx-xxxx-xx-x Cover design by Publication Department, SESRIC. For additional information, contact Statistics Department, SESRIC. i CONTENTS Acronyms
    [Show full text]
  • Multiple Linear Regression
    Multiple Linear Regression Mark Tranmer Mark Elliot 1 Contents Section 1: Introduction............................................................................................................... 3 Exam16 ...................................................................................................................................................... Exam11...................................................................................................................................... 4 Predicted values......................................................................................................................... 5 Residuals.................................................................................................................................... 6 Scatterplot of exam performance at 16 against exam performance at 11.................................. 6 1.3 Theory for multiple linear regression................................................................................... 7 Section 2: Worked Example using SPSS.................................................................................. 10 Section 3: Further topics.......................................................................................................... 36 Stepwise................................................................................................................................... 46 Section 4: BHPS assignment................................................................................................... 46 Reading list.............................................................................................................................
    [Show full text]
  • Geographic Information Systems Correlation Modeling As A
    Boise State University ScholarWorks Anthropology Graduate Projects and Theses Department of Anthropology 6-1-2011 Geographic Information Systems Correlation Modeling as a Management Tool in the Study Effects of Environmental Variables’ Effects on Cultural Resources Brian Wallace Boise State University GEOGRAPHIC INFORMATION SYSTEMS CORRELATION MODELING AS A MANAGEMENT TOOL IN THE STUDY EFFECTS OF ENVIRONMENTAL VARIABLES’ EFFECTS ON CULTURAL RESOURCES by Brian N. Wallace A Project Submitted in Partial Fulfillment Of the Requirements for the Degree of Master of Applied Anthropology Boise State University June 2011 BOISE STATE UNIVERSITY GRADUATE COLLEGE DEFENSE COMMITTEE APPROVAL of the project submitted by Brian N. Wallace The project presented by Brian N. Wallace entitled Geographic Information Systems Correlation Modeling as a Management Tool in the Study Effects of Environmental Variables’ Effects on Cultural Resources is hereby approved: ______________________________________________________ Mark G. Plew Date Advisor ______________________________________________________ John Ziker Date Committee Member ______________________________________________________ Margaret A. Streeter Date Committee Member ______________________________________________________ John R. (Jack) Pelton Date Dean of the Graduate College DEDICATION To my parents Jerry and Cheryl Wallace ii ACKNOWLEDGMENTS The author would like to express his appreciation to those individuals and entities who contributed to the completion of this thesis. Dr. Mark Plew is owed a great debt of gratitude for his invaluable advice, guidance, and friendship throughout my graduate experience. It is because of his helpful suggestions both for this paper and his mentorship over the last few years that have allowed me succeed beyond my own expectations. To the Cultural Resource and GIS staff of the Boise District of the Bureau of Land Management (BLM) whom allowed for access to the necessary data to run analyses successfully and for helpful guidance along the way.
    [Show full text]
  • Bivariate Analysis: the Statistical Analysis of the Relationship Between Two Variables
    bivariate analysis: The statistical analysis of the relationship between two variables. cell frequency: The number of cases in a cell of a cross-tabulation (contingency table). chi-square (χ2) test for independence: A test of statistical significance used to assess the likelihood that an observed association between two variables could have occurred by chance. consistency checking: A data-cleaning procedure involving checking for unreasonable patterns of responses, such as a 12-year-old who voted in the last US presidential election. correlation coefficient: A statistical measure of the strength and direction of a linear relationship between two variables; it may vary from −1 to 0 to +1. data cleaning: The detection and correction of errors in a computer datafile that may have occurred during data collection, coding, and/or data entry. data matrix: The form of a computer datafile, with rows as cases and columns as variables; each cell represents the value of a particular variable (column) for a particular case (row). data processing: The preparation of data for analysis. descriptive statistics: Procedures for organizing and summarizing data. dummy variable: A variable or set of variable categories recoded to have values of 0 and 1. Dummy coding may be applied to nominal- or ordinal-scale variables for the purpose of regression or other numerical analysis. frequency distribution: A tabulation of the number of cases falling into each category of a variable. histogram: A graphic display in which the height of a vertical bar represents the frequency or percentage of cases in each category of an interval/ratio variable. imputation: A procedure for handling missing data in which missing values are assigned based on other information, such as the sample mean or known values of other variables.
    [Show full text]
  • A Statistical Study to Identify the Risk Factors of Heart Attack
    tri ome cs & Bi B f i o o l s t a a n t Fatima et al., J Biom Biostat 2019, 10:2 r i s u t i o c J s Journal of Biometrics & Biostatistics ISSN: 2155-6180 Research Article Article OpenOpen Access Access A Statistical Study to Identify the Risk Factors of Heart Attack Zoha Fatima, Itrat Batool Naqvi* and Sharoon Hanook Department of Statistics, Forman Christian College, Lahore, Pakistan Abstract A statistical study has been conducted to identify the risk factors of heart attack. The study design used in this research is an observational cross sectional. A semi structured questionnaire was designed and surveyed consisting of 25 questions which were filled from 246 patients from two hospitals ‘Gulab Devi’ and ‘Jinnah Hosptial’ Lahore, Pakistan. Respondents were asked questions regarding some of the possible reasons that may cause heart attack. Out of 246 patients, 123 were cases (people who had a heart attack) and remaining 123 were control (people who only had chest pain). We took 123 patients in each group because we needed comparison. Spss and R SOFTWARE were used to determine results of this research. By using univariate, bivariate and multivariate analysis it was observed that the significant factors from model are diabetes blood pressure, sweating, heart attack before, age, severity of pain, medication and pressure of the work. Keywords: Statistical study; Heart attack; Patients; Risk factors Determination of sample size p(1− pz) 2 Introduction n = where, e2 Loss of a loved one can never be forgotten. Forgetting the pain of losing someone is almost as difficult as forgetting the person.
    [Show full text]
  • Introducing the GLIMMIX Procedure for Generalized Linear Mixed Models Oliver Schabenberger, SAS Institute Inc., Cary, NC
    NESUG 18 Analysis Introducing the GLIMMIX Procedure for Generalized Linear Mixed Models Oliver Schabenberger, SAS Institute Inc., Cary, NC ABSTRACT This paper describes a new SAS/STAT procedure for fitting models to non-normal or normal data with correlations or nonconstant variability. The GLIMMIX procedure is an add-on for the SAS/STAT product in SAS 9.1 on the Windows platform. PROC GLIMMIX extends the SAS mixed model tools in a number of ways. For example, it • models data from non-Gaussian distributions • implements low-rank smoothing based on mixed models • provides new features for LS-means comparisons and display • enables you to use SAS programming statements to compute model effects, or to define link and variance functions • fits models to multivariate data in which observations do not all have the same distribution or link Applications of the GLIMMIX procedure include estimating trends in disease rates, modeling counts or proportions over time in a clinical trial, predicting probability of occurrence in time series and spatial data, and joint modeling of correlated binary and continuous data. This paper describes generalized linear mixed models and how to use the GLIMMIX procedure for estima- tion, inference, and prediction. INTRODUCTION The GLIMMIX procedure is a new procedure in SAS/STAT software. It is an add-on for the SAS/STAT product in SAS 9.1 on the Windows platform. It is currently downloadable for the SAS 9.1 release from Software Downloads at support.sas.com. PROC GLIMMIX performs estimation and statistical inference for generalized linear mixed models (GLMMs). A generalized linear mixed model is a statistical model that extends the class of generalized linear models (GLMs) by incorporating normally distributed random effects.
    [Show full text]
  • Statistical Analysis Plan (SAP) Intention-To-Treat Analysis
    EFFECTIVENESS OF A BRIEF INFORMATION ABOUT ADVANCE DIRECTIVES IN PRIMARY CARE: A RANDOMIZED CLINICAL TRIAL Document Date: September 14, 2017 Statistical Analysis Plan (SAP) Intention-to-treat analysis. No intermediate analysis is planned. A bilateral significance level of 5%, 95% CI and 80% power will be used. The SPSS V21 program will be used. Analysis of efficacy of unadjusted parallel clinical trials. Data will be analyzed according to the CONSORT guidance and comparisons between groups will be based on the intention-to-treat principle. First: analysis of the baseline comparability of the study groups in relation to the variables studied. Descriptive statistics of all variables collected. The Student's t test or the Mann- Whitney U test (according to the frequency distribution of the variables studied) will be used to compare continuous variables, and Chi-square or Fisher's exact test for comparison of categorical variables. In the case of finding a very different distribution of the independent baseline variables (1st visit) between the two groups, which would indicate an obvious selection bias despite randomization, the possibility of analyzing as a cohort study by means of propensity score techniques . • Main objective "To assess the effect of brief oral and written information on the Advance Directives (ADs) given by primary care physicians, compared to usual clinical practice, on the proportion of persons interested in or performing VAD in 3 months in a heterogeneous group of patients (different ages and ethnicities) who go to a previous appointment ": inferential analysis of effectiveness, analysis of proportions of two samples. A multivariate logistic regression analysis with the variables of interest or realization of the yes / no VAS as the dependent variable will be performed and the group assigned as an independent variable, adjusting for the potential confounding factors.
    [Show full text]
  • Univariate Analyses Can Be Used for Which of the Following
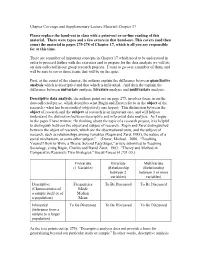
    Chapter Coverage and Supplementary Lecture Material: Chapter 17 Please replace the hand-out in class with a print-out or on-line reading of this material. There were typos and a few errors in that hand-out. This covers (and then some) the material in pages 275-278 of Chapter 17, which is all you are responsible for at this time. There are a number of important concepts in Chapter 17 which need to be understood in order to proceed further with the exercises and to prepare for the data analysis we will do on data collected in our group research projects. I want to go over a number of them, and will be sure to cover those items that will be on the quiz. First, at the outset of the chapter, the authors explain the difference between quantitative analysis which is descriptive and that which is inferential. And then the explain the difference between univariate analysis, bivariate analysis and multivariate analysis. Descriptive data analysis, the authors point out on page 275, involves focus in on the data collected per se, which describes what Ragin and Zaret refer to as the object of the research - what has been studied (objectively one hopes). This distinction between the object of research and the subject of research is an important one, and will help us understand the distinction between descriptive and inferential data analysis. As I argue in the paper I have written: “In thinking about the topic of a research project, it is helpful to distinguish between the object and subject of research.
    [Show full text]