DOCSLIB.ORG

University of Leicester, Msc Medical Statistics, Thesis, Wilmar

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
University of Leicester, Msc Medical Statistics, Thesis, Wilmar Thesis MSc in Medical Statistics Department of Health Sciences University of Leicester, United Kingdom Application of Bayesian hierarchical generalized linear models using weakly informative prior distributions to identify rare genetic variant effects on blood pressure Wilmar Igl March 2015 Summary Background Currently rare genetic variants are discussed as a source of \missing heritability" of complex traits. Bayesian hierarchical models were proposed as an efficient method for the estimation and aggregation of conditional effects of rare variants. Here, such models are applied to identify rare variant effects on blood pressure. Methods Empirical data provided by the Genetic Analysis Workshop 19 (2014) included 1,851 Mexican-American individuals with diastolic blood pressure (DBP), systolic blood pressure (SBP), hypertension (HTN) and 461,868 variants from whole- exome sequencing of odd-numbered chromosomes. Bayesian hierarchical generalized linear models using weakly informative prior distributions were applied. Results Associations of rare variants chr1:204214013 (estimate = 39.6, Credible In- terval (CrI) 95% = [25.3, 53.9], Bayesian p = 6:8 × 10−8) in the PLEKHA6 gene and chr11:118518698 (estimate = 32.2, CrI95% = [20.6, 43.9], Bayesian p = 7:0 × 10−8) in the PHLEDB1 gene were identified. Joint effects of grouped rare variants on DBP in 23 genes (Bayesian p = [8:8 × 10−14, 9:3 × 10−8]) and on SBP in 21 genes (Bayesian p = [8:6 × 10−12, 7:8 × 10−8]) in pathways related to hemostasis, sodi- um/calcium transport, ciliary activity, and others were found. No association with hypertension was detected. Conclusions Bayesian hierarchical generalized linear models with weakly informa- tive priors can successfully be applied in exome-wide genetic association analyses of rare variants. ii Acknowledgments I would like to thank my supervisors Professor John Thompson, PhD, and Louise Wain, PhD, for developing this challenging project with me and for supporting it with their encouragement and advice. Additionally, I am grateful to the Department of Health Sciences and all lecturers and tutors for providing such a stimulating and friendly environment for the Master of Medical Statistics program. Especially, Stephanie Hubbard as the course director contributed largely to the success of this program. Furthermore, I would like to express my gratitude to the Department of Health Sciences for supporting the presentation of first results of my thesis at the Genetic Analysis Workshop 19, Vienna, from August 24 to 27, 2014, with a travel grant. Moreover, I want to thank my former employer, Professor Iris Heid, University of Regensburg, for enabling me to attend the courses of the Master of Medical Statistics program and for granting me special leave to complete my thesis. Finally, freely adapting another proverb I want to emphasize that \It takes a village to write a thesis.". Therefore, I would like to give my special thanks to my partner Bettina, our parents, especially Lieselotte, our friend Petra, and all others who made sure that I had the time to work and study and that my son Moritz always found himself in a safe, understanding, and loving environment. F¨urth,March 2015 Wilmar Igl iii Table of contents Summary ii Acknowledgments iii Table of contents iv List of tables viii List of figures xiii 1 Introduction 1 1.1 Missing heritability, rare variants, and Bayesian statistics . .1 1.2 Previous publications . .4 1.3 Overview . .4 2 Biological and medical background 5 2.1 Definitions . .5 2.2 General epidemiology . .6 2.3 Genetic epidemiology . .7 2.3.1 Rare and common genetic variation . .7 2.3.2 Genetics of blood pressure . .7 3 Statistical background 10 3.1 Bayesian and frequentist statistics . 10 3.2 Bayes theorem . 11 3.3 Bayes factors . 12 iv Table of contents 3.4 Bayesian p values . 15 3.4.1 Frequentist p values . 15 3.4.2 The one-sided testing problem . 16 3.4.3 Classes of prior distributions . 17 3.4.4 Non-informative and weakly informative priors . 18 3.4.5 Uniformity of p values . 20 3.4.6 Summary . 20 4 Bayesian hierarchical generalized linear models 21 4.1 Overview . 21 4.2 Linear predictor, link function, and error distribution . 23 4.3 Prior distributions . 25 4.3.1 Variant effects . 25 4.3.2 Group effects . 27 4.3.3 Covariate effects, intercept, and dispersion . 28 4.4 Estimation algorithm (IWLS-EM) . 28 4.5 Bayesian p values . 31 4.5.1 Individual variants . 31 4.5.2 Grouped variants . 32 5 Methods 34 5.1 Data . 34 5.1.1 Simulated data . 34 5.1.2 GAW19 Data . 35 5.2 Statistical models . 40 5.2.1 Frequentist analysis of individual variants . 40 5.2.2 Bayesian analysis of multiple variants . 41 5.2.3 Multiple testing . 42 5.2.4 Missing data . 42 5.2.5 Correction of ethnicity and relatedness . 42 5.2.6 Criteria for model evaluation . 43 v Table of contents 5.3 Software . 44 5.3.1 EPACTS . 44 5.3.2 R/BhGLM . 45 5.3.3 Other . 45 5.4 Hardware . 46 6 Results 47 6.1 Descriptives . 47 6.1.1 Simulated data I . 47 6.1.2 Simulated data II (GAW 19) . 48 6.1.3 Empirical data (GAW 19) . 48 6.2 Simulated data I . 50 6.2.1 Frequentist single-variant analysis . 51 6.2.2 Bayesian hierarchical multiple-variant analysis . 52 6.2.3 Summary . 58 6.3 Simulated data II (GAW 19) . 59 6.3.1 Frequentist single-variant analysis . 59 6.3.2 Bayesian hierarchical multiple-variant analysis . 61 6.3.3 Summary . 64 6.4 Empirical data (GAW 19) . 66 6.4.1 Frequentist single-variant analysis . 66 6.4.2 Bayesian hierarchical multiple-variant analysis . 70 6.4.3 Comparison of single and multiple variant analysis . 80 7 Discussion 86 7.1 Summary . 86 7.2 Statistical models . 87 7.2.1 Frequentist models . 87 7.2.2 Bayesian hierarchical models . 88 7.2.3 Comparison of applied models . 89 vi Table of contents 7.3 Genetics of blood pressure . 90 7.3.1 Individual variant effects . 91 7.3.2 Grouped variant effects . 92 7.4 Modelling of prior biological information . 96 7.5 Strengths and weaknesses . 98 7.5.1 Topic . 98 7.5.2 Method . 98 7.5.3 Model . 99 7.6 Conclusion . 99 References 100 A Appendix 114 A.1 Generalized linear model of the normal distribution . 115 A.2 Generalized linear model of the binomial distribution . 118 A.3 Examples of prior distributions . 122 A.4 Supplementary tables . 128 A.5 Supplementary figures . 143 vii List of tables 2.1 Top ten genes or gene regions associated with blood pressure, hyper- tension, or hypotension according to the GWAS catalog (Welter et al. (2014), retrieved December 8, 2014). Genes are sorted by p value of the index variant. .8 3.1 Scale of interpretation of the Bayes factor according to Kass and Raftery (1995) (adapted from Wagenmakers et al. (2008)) . 13 6.1 Descriptives of simulated data II (1,943 individuals, GAW19) . 49 6.2 Descriptives of the empirical data (1,943 individuals, GAW19) . 50 6.3 Genetic variants in the GAW19 data (1,943 individuals) . 50 6.4 Table of average coefficients of a frequentist normal linear model of simulated systolic blood pressure (SBP). SBP was predicted from individual variants (model 1), unweighted genetic scores (model 2), or weighted genetic scores (model 3). Analysis was performed in 1,000 datasets with 10,000 individuals without genetic effects (simulated data Ia). 52 6.5 Table of average coefficients of a reduced Bayesian hierarchical model predicting simulated systolic blood pressure using weakly informative prior Cauchy (0, 1) distributions. Analysis was performed in 1,000 samples with 10,000 individuals without genetic effects (simulated data Ia). Associations between systolic blood pressure and individual variant effects (model 1), average variant effects (model 2), or joint variant effects (model 3) of grouped variants were tested. 54 viii List of tables 6.6 Table of average coefficients of a full Bayesian hierarchical model pre- dicting systolic blood pressure using weakly informative prior Cauchy (0, 1) distributions for group effects and Cauchy distributions with selected parameters for individual variants. Analysis was performed in 1,000 samples with 10,000 individuals without genetic effects (sim- ulated data Ia). 55 6.7 Table of average coefficients of a full Bayesian hierarchical model pre- dicting simulated systolic blood pressure using weakly informative prior Cauchy (0, 1) distributions for group effects and Cauchy dis- tributions with selected parameters for individual variants. Analysis was performed in 1,000 samples with 10,000 individuals with genetic effects (simulated data Ib). 58 6.8 Overview on genome-wide significant associations in 128 candidate genes with non-null effects and nominally significant associations in 1,000 genes with null effects in simulated data II (GAW19) . 65 6.9 Associations of top ten variants with observed diastolic blood pressure using a normal linear model in empirical GAW19 data (sorted by p value) ................................... 67 6.10 Associations of top ten variants with observed systolic blood pressure using a normal linear model in empirical GAW19 data (sorted by p value) ................................... 68 6.11 Associations of top ten variants with observed hypertension using the Firth logistic model in empirical GAW19 data (sorted by p value) . 69 6.12 Associations of top ten variants associated with observed diastolic blood pressure using a reduced Bayesian hierarchical generalized lin- ear model (normal) in empirical GAW19 data (sorted by Bayesian p value) ................................... 71 6.13 Associations of top ten variants with observed systolic blood pres- sure using a reduced Bayesian hierarchical generalized linear model (normal) in empirical GAW19 data (sorted by Bayesian p value) .
Load more

Recommended publications
  • Entrez Symbols Name Termid Termdesc 117553 Uba3,Ube1c
    Entrez Symbols Name TermID TermDesc 117553 Uba3,Ube1c ubiquitin-like modifier activating enzyme 3 GO:0016881 acid-amino acid ligase activity 299002 G2e3,RGD1310263 G2/M-phase specific E3 ubiquitin ligase GO:0016881 acid-amino acid ligase activity 303614 RGD1310067,Smurf2 SMAD specific E3 ubiquitin protein ligase 2 GO:0016881 acid-amino acid ligase activity 308669 Herc2 hect domain and RLD 2 GO:0016881 acid-amino acid ligase activity 309331 Uhrf2 ubiquitin-like with PHD and ring finger domains 2 GO:0016881 acid-amino acid ligase activity 316395 Hecw2 HECT, C2 and WW domain containing E3 ubiquitin protein ligase 2 GO:0016881 acid-amino acid ligase activity 361866 Hace1 HECT domain and ankyrin repeat containing, E3 ubiquitin protein ligase 1 GO:0016881 acid-amino acid ligase activity 117029 Ccr5,Ckr5,Cmkbr5 chemokine (C-C motif) receptor 5 GO:0003779 actin binding 117538 Waspip,Wip,Wipf1 WAS/WASL interacting protein family, member 1 GO:0003779 actin binding 117557 TM30nm,Tpm3,Tpm5 tropomyosin 3, gamma GO:0003779 actin binding 24779 MGC93554,Slc4a1 solute carrier family 4 (anion exchanger), member 1 GO:0003779 actin binding 24851 Alpha-tm,Tma2,Tmsa,Tpm1 tropomyosin 1, alpha GO:0003779 actin binding 25132 Myo5b,Myr6 myosin Vb GO:0003779 actin binding 25152 Map1a,Mtap1a microtubule-associated protein 1A GO:0003779 actin binding 25230 Add3 adducin 3 (gamma) GO:0003779 actin binding 25386 AQP-2,Aqp2,MGC156502,aquaporin-2aquaporin 2 (collecting duct) GO:0003779 actin binding 25484 MYR5,Myo1e,Myr3 myosin IE GO:0003779 actin binding 25576 14-3-3e1,MGC93547,Ywhah
    [Show full text]
  • Download The
    PROBING THE INTERACTION OF ASPERGILLUS FUMIGATUS CONIDIA AND HUMAN AIRWAY EPITHELIAL CELLS BY TRANSCRIPTIONAL PROFILING IN BOTH SPECIES by POL GOMEZ B.Sc., The University of British Columbia, 2002 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE in THE FACULTY OF GRADUATE STUDIES (Experimental Medicine) THE UNIVERSITY OF BRITISH COLUMBIA (Vancouver) January 2010 © Pol Gomez, 2010 ABSTRACT The cells of the airway epithelium play critical roles in host defense to inhaled irritants, and in asthma pathogenesis. These cells are constantly exposed to environmental factors, including the conidia of the ubiquitous mould Aspergillus fumigatus, which are small enough to reach the alveoli. A. fumigatus is associated with a spectrum of diseases ranging from asthma and allergic bronchopulmonary aspergillosis to aspergilloma and invasive aspergillosis. Airway epithelial cells have been shown to internalize A. fumigatus conidia in vitro, but the implications of this process for pathogenesis remain unclear. We have developed a cell culture model for this interaction using the human bronchial epithelium cell line 16HBE and a transgenic A. fumigatus strain expressing green fluorescent protein (GFP). Immunofluorescent staining and nystatin protection assays indicated that cells internalized upwards of 50% of bound conidia. Using fluorescence-activated cell sorting (FACS), cells directly interacting with conidia and cells not associated with any conidia were sorted into separate samples, with an overall accuracy of 75%. Genome-wide transcriptional profiling using microarrays revealed significant responses of 16HBE cells and conidia to each other. Significant changes in gene expression were identified between cells and conidia incubated alone versus together, as well as between GFP positive and negative sorted cells.
    [Show full text]
  • Supplementary Table 1: Adhesion Genes Data Set
    Supplementary Table 1: Adhesion genes data set PROBE Entrez Gene ID Celera Gene ID Gene_Symbol Gene_Name 160832 1 hCG201364.3 A1BG alpha-1-B glycoprotein 223658 1 hCG201364.3 A1BG alpha-1-B glycoprotein 212988 102 hCG40040.3 ADAM10 ADAM metallopeptidase domain 10 133411 4185 hCG28232.2 ADAM11 ADAM metallopeptidase domain 11 110695 8038 hCG40937.4 ADAM12 ADAM metallopeptidase domain 12 (meltrin alpha) 195222 8038 hCG40937.4 ADAM12 ADAM metallopeptidase domain 12 (meltrin alpha) 165344 8751 hCG20021.3 ADAM15 ADAM metallopeptidase domain 15 (metargidin) 189065 6868 null ADAM17 ADAM metallopeptidase domain 17 (tumor necrosis factor, alpha, converting enzyme) 108119 8728 hCG15398.4 ADAM19 ADAM metallopeptidase domain 19 (meltrin beta) 117763 8748 hCG20675.3 ADAM20 ADAM metallopeptidase domain 20 126448 8747 hCG1785634.2 ADAM21 ADAM metallopeptidase domain 21 208981 8747 hCG1785634.2|hCG2042897 ADAM21 ADAM metallopeptidase domain 21 180903 53616 hCG17212.4 ADAM22 ADAM metallopeptidase domain 22 177272 8745 hCG1811623.1 ADAM23 ADAM metallopeptidase domain 23 102384 10863 hCG1818505.1 ADAM28 ADAM metallopeptidase domain 28 119968 11086 hCG1786734.2 ADAM29 ADAM metallopeptidase domain 29 205542 11085 hCG1997196.1 ADAM30 ADAM metallopeptidase domain 30 148417 80332 hCG39255.4 ADAM33 ADAM metallopeptidase domain 33 140492 8756 hCG1789002.2 ADAM7 ADAM metallopeptidase domain 7 122603 101 hCG1816947.1 ADAM8 ADAM metallopeptidase domain 8 183965 8754 hCG1996391 ADAM9 ADAM metallopeptidase domain 9 (meltrin gamma) 129974 27299 hCG15447.3 ADAMDEC1 ADAM-like,
    [Show full text]
  • Supplementary Table S4. FGA Co-Expressed Gene List in LUAD
    Supplementary Table S4. FGA co-expressed gene list in LUAD tumors Symbol R Locus Description FGG 0.919 4q28 fibrinogen gamma chain FGL1 0.635 8p22 fibrinogen-like 1 SLC7A2 0.536 8p22 solute carrier family 7 (cationic amino acid transporter, y+ system), member 2 DUSP4 0.521 8p12-p11 dual specificity phosphatase 4 HAL 0.51 12q22-q24.1histidine ammonia-lyase PDE4D 0.499 5q12 phosphodiesterase 4D, cAMP-specific FURIN 0.497 15q26.1 furin (paired basic amino acid cleaving enzyme) CPS1 0.49 2q35 carbamoyl-phosphate synthase 1, mitochondrial TESC 0.478 12q24.22 tescalcin INHA 0.465 2q35 inhibin, alpha S100P 0.461 4p16 S100 calcium binding protein P VPS37A 0.447 8p22 vacuolar protein sorting 37 homolog A (S. cerevisiae) SLC16A14 0.447 2q36.3 solute carrier family 16, member 14 PPARGC1A 0.443 4p15.1 peroxisome proliferator-activated receptor gamma, coactivator 1 alpha SIK1 0.435 21q22.3 salt-inducible kinase 1 IRS2 0.434 13q34 insulin receptor substrate 2 RND1 0.433 12q12 Rho family GTPase 1 HGD 0.433 3q13.33 homogentisate 1,2-dioxygenase PTP4A1 0.432 6q12 protein tyrosine phosphatase type IVA, member 1 C8orf4 0.428 8p11.2 chromosome 8 open reading frame 4 DDC 0.427 7p12.2 dopa decarboxylase (aromatic L-amino acid decarboxylase) TACC2 0.427 10q26 transforming, acidic coiled-coil containing protein 2 MUC13 0.422 3q21.2 mucin 13, cell surface associated C5 0.412 9q33-q34 complement component 5 NR4A2 0.412 2q22-q23 nuclear receptor subfamily 4, group A, member 2 EYS 0.411 6q12 eyes shut homolog (Drosophila) GPX2 0.406 14q24.1 glutathione peroxidase
    [Show full text]
  • SNX17 Recruits USP9X to Antagonize MIB1-Mediated Ubiquitination and Degradation of PCM1 During Serum-Starvation-Induced Ciliogenesis
    cells Article SNX17 Recruits USP9X to Antagonize MIB1-Mediated Ubiquitination and Degradation of PCM1 during Serum-Starvation-Induced Ciliogenesis Pengtao Wang 1,2,3,4, Jianhong Xia 2,3, Leilei Zhang 2,3, Shaoyang Zhao 2,3, Shengbiao Li 2,3, Haiyun Wang 2,3, Shan Cheng 4, Heying Li 2,3, Wenguang Yin 2,3, Duanqing Pei 2,3,5,* and Xiaodong Shu 2,3,4,5,6,* 1 School of Life Sciences, University of Science and Technology of China, Hefei 230027, China; [email protected] 2 CAS Key Laboratory of Regenerative Biology, South China Institutes for Stem Cell Biology and Regenerative Medicine, Guangzhou Institutes of Biomedicine and Health, Chinese Academy of Sciences, Guangzhou 510530, China; [email protected] (J.X.); [email protected] (L.Z.); [email protected] (S.Z.); [email protected] (S.L.); [email protected] (H.W.); [email protected] (H.L.); [email protected] (W.Y.) 3 Guangdong Provincial Key Laboratory of Stem Cell and Regenerative Medicine, Guangzhou 510530, China 4 Hefei Institute of Stem Cell and Regenerative Medicine, Guangzhou Institutes of Biomedicine and Health, Chinese Academy of Sciences, Guangzhou 510530, China; [email protected] 5 Guangzhou Regenerative Medicine and Health Guangdong Laboratory (GRMH-GDL), Guangzhou 510005, China 6 Joint School of Life Sciences, Guangzhou Institutes of Biomedicine and Health, Chinese Academy of Sciences, Guangzhou Medical University, Guangzhou 511436, China * Correspondence: [email protected] (D.P.); [email protected] (X.S.); Tel.: +86-20-3201-5310 (X.S.) Academic Editor: Tomer Avidor-Reiss Received: 13 September 2019; Accepted: 27 October 2019; Published: 29 October 2019 Abstract: Centriolar satellites are non-membrane cytoplasmic granules that deliver proteins to centrosome during centrosome biogenesis and ciliogenesis.
    [Show full text]
  • Identification of Unknown Epigenetically Regulated Genes in Non-Small Cell Lung Cancer”
    DIPLOMARBEIT Titel der Diplomarbeit “Identification of unknown epigenetically regulated genes in non-small cell lung cancer” Durchgeführt an der Medizinischen Universität Wien Univ. Klinik für Innere Med. I/Klinische Abteilung für Onkologie Verfasserin Valerie Nadine Babinsky angestrebter akademischer Grad Magistra der Naturwissenschaften (Mag.rer.nat.) Wien, 2011 Studienkennzahl lt. Studienblatt: A 441 Studienrichtung lt. Studienblatt: Mikrobiologie und Genetik Betreuer: Ao.Prof. Dr. Wolfgang Mikulits Table of Content 1 TABLE OF CONTENT 1 Table of Content ............................................................................................................ 2 2 Acknowledgment / Danksagung ..................................................................................... 5 3 Introduction ................................................................................................................... 6 4 Aim of study .................................................................................................................. 7 5 Background .................................................................................................................... 9 5.1 Epigenetics: Histone protein modifications and DNA methylation ......................................... 9 5.1.1 Histone protein modifications ............................................................................................... 10 5.1.2 DNA methylation ..................................................................................................................
    [Show full text]
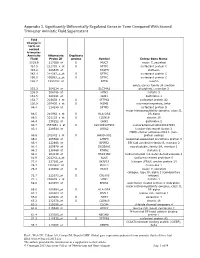
  • Appendix 2. Significantly Differentially Regulated Genes in Term Compared with Second Trimester Amniotic Fluid Supernatant
    Appendix 2. Significantly Differentially Regulated Genes in Term Compared With Second Trimester Amniotic Fluid Supernatant Fold Change in term vs second trimester Amniotic Affymetrix Duplicate Fluid Probe ID probes Symbol Entrez Gene Name 1019.9 217059_at D MUC7 mucin 7, secreted 424.5 211735_x_at D SFTPC surfactant protein C 416.2 206835_at STATH statherin 363.4 214387_x_at D SFTPC surfactant protein C 295.5 205982_x_at D SFTPC surfactant protein C 288.7 1553454_at RPTN repetin solute carrier family 34 (sodium 251.3 204124_at SLC34A2 phosphate), member 2 238.9 206786_at HTN3 histatin 3 161.5 220191_at GKN1 gastrokine 1 152.7 223678_s_at D SFTPA2 surfactant protein A2 130.9 207430_s_at D MSMB microseminoprotein, beta- 99.0 214199_at SFTPD surfactant protein D major histocompatibility complex, class II, 96.5 210982_s_at D HLA-DRA DR alpha 96.5 221133_s_at D CLDN18 claudin 18 94.4 238222_at GKN2 gastrokine 2 93.7 1557961_s_at D LOC100127983 uncharacterized LOC100127983 93.1 229584_at LRRK2 leucine-rich repeat kinase 2 HOXD cluster antisense RNA 1 (non- 88.6 242042_s_at D HOXD-AS1 protein coding) 86.0 205569_at LAMP3 lysosomal-associated membrane protein 3 85.4 232698_at BPIFB2 BPI fold containing family B, member 2 84.4 205979_at SCGB2A1 secretoglobin, family 2A, member 1 84.3 230469_at RTKN2 rhotekin 2 82.2 204130_at HSD11B2 hydroxysteroid (11-beta) dehydrogenase 2 81.9 222242_s_at KLK5 kallikrein-related peptidase 5 77.0 237281_at AKAP14 A kinase (PRKA) anchor protein 14 76.7 1553602_at MUCL1 mucin-like 1 76.3 216359_at D MUC7 mucin 7,
    [Show full text]
  • USP9X Regulates Centrosome Duplication and Promotes Breast Carcinogenesis
    ARTICLE Received 21 Feb 2016 | Accepted 31 Jan 2017 | Published 31 Mar 2017 DOI: 10.1038/ncomms14866 OPEN USP9X regulates centrosome duplication and promotes breast carcinogenesis Xin Li1,*, Nan Song1,*, Ling Liu1, Xinhua Liu1, Xiang Ding2, Xin Song3, Shangda Yang1, Lin Shan1, Xing Zhou1, Dongxue Su1, Yue Wang1, Qi Zhang1, Cheng Cao1, Shuai Ma1,NaYu1, Fuquan Yang2, Yan Wang1, Zhi Yao4, Yongfeng Shang1,5 & Lei Shi1,4 Defective centrosome duplication is implicated in microcephaly and primordial dwarfism as well as various ciliopathies and cancers. Yet, how the centrosome biogenesis is regulated remains poorly understood. Here we report that the X-linked deubiquitinase USP9X is physically associated with centriolar satellite protein CEP131, thereby stabilizing CEP131 through its deubiquitinase activity. We demonstrate that USP9X is an integral component of centrosome and is required for centrosome biogenesis. Loss-of-function of USP9X impairs centrosome duplication and gain-of-function of USP9X promotes centrosome amplification and chromosome instability. Significantly, USP9X is overexpressed in breast carcinomas, and its level of expression is correlated with that of CEP131 and higher histologic grades of breast cancer. Indeed, USP9X, through regulation of CEP131 abundance, promotes breast carcino- genesis. Our experiments identify USP9X as an important regulator of centrosome biogenesis and uncover a critical role for USP9X/CEP131 in breast carcinogenesis, supporting the pursuit of USP9X/CEP131 as potential targets for breast cancer intervention. 1 2011 Collaborative Innovation Center of Tianjin for Medical Epigenetics, Tianjin Key Laboratory of Medical Epigenetics, Department of Biochemistry and Molecular Biology, School of Basic Medical Sciences, Tianjin Medical University, Tianjin 300070, China. 2 Laboratory of Proteomics, Institute of Biophysics, Chinese Academy of Sciences, Beijing 100101, China.
    [Show full text]
  • Application of Microrna Database Mining in Biomarker Discovery and Identification of Therapeutic Targets for Complex Disease
    Article Application of microRNA Database Mining in Biomarker Discovery and Identification of Therapeutic Targets for Complex Disease Jennifer L. Major, Rushita A. Bagchi * and Julie Pires da Silva * Department of Medicine, Division of Cardiology, University of Colorado Anschutz Medical Campus, Aurora, CO 80045, USA; [email protected] * Correspondence: [email protected] (R.A.B.); [email protected] (J.P.d.S.) Supplementary Tables Methods Protoc. 2021, 4, 5. https://doi.org/10.3390/mps4010005 www.mdpi.com/journal/mps Methods Protoc. 2021, 4, 5. https://doi.org/10.3390/mps4010005 2 of 25 Table 1. List of all hsa-miRs identified by Human microRNA Disease Database (HMDD; v3.2) analysis. hsa-miRs were identified using the term “genetics” and “circulating” as input in HMDD. Targets CAD hsa-miR-1 Targets IR injury hsa-miR-423 Targets Obesity hsa-miR-499 hsa-miR-146a Circulating Obesity Genetics CAD hsa-miR-423 hsa-miR-146a Circulating CAD hsa-miR-149 hsa-miR-499 Circulating IR Injury hsa-miR-146a Circulating Obesity hsa-miR-122 Genetics Stroke Circulating CAD hsa-miR-122 Circulating Stroke hsa-miR-122 Genetics Obesity Circulating Stroke hsa-miR-26b hsa-miR-17 hsa-miR-223 Targets CAD hsa-miR-340 hsa-miR-34a hsa-miR-92a hsa-miR-126 Circulating Obesity Targets IR injury hsa-miR-21 hsa-miR-423 hsa-miR-126 hsa-miR-143 Targets Obesity hsa-miR-21 hsa-miR-223 hsa-miR-34a hsa-miR-17 Targets CAD hsa-miR-223 hsa-miR-92a hsa-miR-126 Targets IR injury hsa-miR-155 hsa-miR-21 Circulating CAD hsa-miR-126 hsa-miR-145 hsa-miR-21 Targets Obesity hsa-mir-223 hsa-mir-499 hsa-mir-574 Targets IR injury hsa-mir-21 Circulating IR injury Targets Obesity hsa-mir-21 Targets CAD hsa-mir-22 hsa-mir-133a Targets IR injury hsa-mir-155 hsa-mir-21 Circulating Stroke hsa-mir-145 hsa-mir-146b Targets Obesity hsa-mir-21 hsa-mir-29b Methods Protoc.
    [Show full text]
  • Caracterización De Complejos CDK-Ciclina Atípicos Humanos Eva Quandt Herrera
    Caracterización de complejos CDK-Ciclina atípicos humanos Eva Quandt Herrera ADVERTIMENT. La consulta d’aquesta tesi queda condicionada a l’acceptació de les següents condicions d'ús: La difusió d’aquesta tesi per mitjà del servei TDX (www.tesisenxarxa.net) ha estat autoritzada pels titulars dels drets de propietat intel·lectual únicament per a usos privats emmarcats en activitats d’investigació i docència. No s’autoritza la seva reproducció amb finalitats de lucre ni la seva difusió i posada a disposició des d’un lloc aliè al servei TDX. No s’autoritza la presentació del seu contingut en una finestra o marc aliè a TDX (framing). Aquesta reserva de drets afecta tant al resum de presentació de la tesi com als seus continguts. En la utilització o cita de parts de la tesi és obligat indicar el nom de la persona autora. ADVERTENCIA. La consulta de esta tesis queda condicionada a la aceptación de las siguientes condiciones de uso: La difusión de esta tesis por medio del servicio TDR (www.tesisenred.net) ha sido autorizada por los titulares de los derechos de propiedad intelectual únicamente para usos privados enmarcados en actividades de investigación y docencia. No se autoriza su reproducción con finalidades de lucro ni su difusión y puesta a disposición desde un sitio ajeno al servicio TDR. No se autoriza la presentación de su contenido en una ventana o marco ajeno a TDR (framing). Esta reserva de derechos afecta tanto al resumen de presentación de la tesis como a sus contenidos. En la utilización o cita de partes de la tesis es obligado indicar el nombre de la persona autora.
    [Show full text]
  • Characterizing Genomic Duplication in Autism Spectrum Disorder by Edward James Higginbotham a Thesis Submitted in Conformity
    Characterizing Genomic Duplication in Autism Spectrum Disorder by Edward James Higginbotham A thesis submitted in conformity with the requirements for the degree of Master of Science Graduate Department of Molecular Genetics University of Toronto © Copyright by Edward James Higginbotham 2020 i Abstract Characterizing Genomic Duplication in Autism Spectrum Disorder Edward James Higginbotham Master of Science Graduate Department of Molecular Genetics University of Toronto 2020 Duplication, the gain of additional copies of genomic material relative to its ancestral diploid state is yet to achieve full appreciation for its role in human traits and disease. Challenges include accurately genotyping, annotating, and characterizing the properties of duplications, and resolving duplication mechanisms. Whole genome sequencing, in principle, should enable accurate detection of duplications in a single experiment. This thesis makes use of the technology to catalogue disease relevant duplications in the genomes of 2,739 individuals with Autism Spectrum Disorder (ASD) who enrolled in the Autism Speaks MSSNG Project. Fine-mapping the breakpoint junctions of 259 ASD-relevant duplications identified 34 (13.1%) variants with complex genomic structures as well as tandem (193/259, 74.5%) and NAHR- mediated (6/259, 2.3%) duplications. As whole genome sequencing-based studies expand in scale and reach, a continued focus on generating high-quality, standardized duplication data will be prerequisite to addressing their associated biological mechanisms. ii Acknowledgements I thank Dr. Stephen Scherer for his leadership par excellence, his generosity, and for giving me a chance. I am grateful for his investment and the opportunities afforded me, from which I have learned and benefited. I would next thank Drs.
    [Show full text]
  • Rabbit Anti-AZI1/FITC Conjugated Antibody-SL12977R-FITC
    SunLong Biotech Co.,LTD Tel: 0086-571- 56623320 Fax:0086-571- 56623318 E-mail:[email protected] www.sunlongbiotech.com Rabbit Anti-AZI1/FITC Conjugated antibody SL12977R-FITC Product Name: Anti-AZI1/FITC Chinese Name: FITC标记的中心体蛋白AZI1抗体 5 azacytidine induced 1; 5-azacytidine induced 1; 5-azacytidine-induced protein 1; AZ1; Azi; Azi1; AZI1_HUMAN; Centrosomal protein 131 kDa; Centrosomal protein of 131 Alias: kDa; Centrosomal protein of 131 kDa; Cep131; Cep131; KIAA1118; OTTMUSP00000004498; Pre-acrosome localization protein 1; RP23 37J21.1. Organism Species: Rabbit Clonality: Polyclonal React Species: Human,Mouse,Rat,Chicken,Pig,Cow,Horse,Sheep, ICC=1:50-200IF=1:50-200 Applications: not yet tested in other applications. optimal dilutions/concentrations should be determined by the end user. Molecular weight: 122kDa Form: Lyophilized or Liquid Concentration: 1mg/ml immunogen: KLH conjugated synthetic peptide derived from human AZI1 Lsotype: IgG Purification: affinitywww.sunlongbiotech.com purified by Protein A Storage Buffer: 0.01M TBS(pH7.4) with 1% BSA, 0.03% Proclin300 and 50% Glycerol. Store at -20 °C for one year. Avoid repeated freeze/thaw cycles. The lyophilized antibody is stable at room temperature for at least one month and for greater than a year Storage: when kept at -20°C. When reconstituted in sterile pH 7.4 0.01M PBS or diluent of antibody the antibody is stable for at least two weeks at 2-4 °C. background: AZI1 is a 1,083 amino acid protein that may play a role in spermatogenesis. AZI1 is most highly expressed in spinal cord, followed by testis, ovary, amygdala, cerebellum Product Detail: and thalamus.
    [Show full text]