Responses to Anonymous Referee #1' Comments
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Summary of 2014 NW Pacific Typhoon Season and Verification of Authors’ Seasonal Forecasts
Summary of 2014 NW Pacific Typhoon Season and Verification of Authors’ Seasonal Forecasts Issued: 27th January 2015 by Dr Adam Lea and Professor Mark Saunders Dept. of Space and Climate Physics, UCL (University College London), UK. Summary The 2014 NW Pacific typhoon season was characterised by activity slightly below the long-term (1965-2013) norm. The TSR forecasts over-predicted activity but mostly to within the forecast error. The Tropical Storm Risk (TSR) consortium presents a validation of their seasonal forecasts for the NW Pacific basin ACE index, numbers of intense typhoons, numbers of typhoons and numbers of tropical storms in 2014. These forecasts were issued on the 6th May, 3rd July and the 5th August 2014. The 2014 NW Pacific typhoon season ran from 1st January to 31st December. Features of the 2014 NW Pacific Season • Featured 23 tropical storms, 12 typhoons, 8 intense typhoons and a total ACE index of 273. These numbers were respectively 12%, 25%, 0% and 7% below their corresponding long-term norms. Seven out of the last eight years have now had a NW Pacific ACE index below the 1965-2013 climate norm value of 295. • The peak months of August and September were unusually quiet, with only one typhoon forming within the basin (Genevieve formed in the NE Pacific and crossed into the NW Pacific basin as a hurricane). Since 1965 no NW Pacific typhoon season has seen less than two typhoons develop within the NW Pacific basin during August and September. This lack of activity in 2014 was in part caused by an unusually strong and persistent suppressing phase of the Madden-Julian Oscillation. -
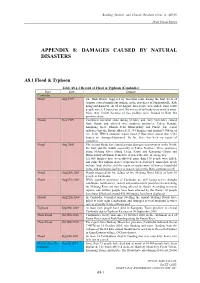
Appendix 8: Damages Caused by Natural Disasters
Building Disaster and Climate Resilient Cities in ASEAN Draft Finnal Report APPENDIX 8: DAMAGES CAUSED BY NATURAL DISASTERS A8.1 Flood & Typhoon Table A8.1.1 Record of Flood & Typhoon (Cambodia) Place Date Damage Cambodia Flood Aug 1999 The flash floods, triggered by torrential rains during the first week of August, caused significant damage in the provinces of Sihanoukville, Koh Kong and Kam Pot. As of 10 August, four people were killed, some 8,000 people were left homeless, and 200 meters of railroads were washed away. More than 12,000 hectares of rice paddies were flooded in Kam Pot province alone. Floods Nov 1999 Continued torrential rains during October and early November caused flash floods and affected five southern provinces: Takeo, Kandal, Kampong Speu, Phnom Penh Municipality and Pursat. The report indicates that the floods affected 21,334 families and around 9,900 ha of rice field. IFRC's situation report dated 9 November stated that 3,561 houses are damaged/destroyed. So far, there has been no report of casualties. Flood Aug 2000 The second floods has caused serious damages on provinces in the North, the East and the South, especially in Takeo Province. Three provinces along Mekong River (Stung Treng, Kratie and Kompong Cham) and Municipality of Phnom Penh have declared the state of emergency. 121,000 families have been affected, more than 170 people were killed, and some $10 million in rice crops has been destroyed. Immediate needs include food, shelter, and the repair or replacement of homes, household items, and sanitation facilities as water levels in the Delta continue to fall. -

Minnesota Weathertalk Newsletter for Friday, January 3, 2014
Minnesota WeatherTalk Newsletter for Friday, January 3, 2014 To: MPR's Morning Edition From: Mark Seeley, Univ. of Minnesota, Dept of Soil, Water, and Climate Subject: Minnesota WeatherTalk Newsletter for Friday, January 3, 2014 HEADLINES -December 2013 was climate near historic for northern communities -Cold start to 2014 -Weekly Weather potpourri -MPR listener questions -Almanac for January 3rd -Past weather -Outlook Topic: December 2013 near historic for far north In assessing the climate for December 2013 it should be said that from the standpoint of cold temperatures the month was quite historic for many northern Minnesota communities, especially due to the Arctic cold that prevailed over the last few days of the month. Minnesota reported the coldest temperature in the 48 contiguous states thirteen times during the month, the highest frequency among all 48 states. Many northern observers saw overnight temperatures drop below -30 degrees F on several occasions. The mean monthly temperature for December from several communities ranked among the coldest Decembers ever. A sample listing includes: -4.1 F at International Falls, 2nd coldest all-time 4.6 F at Duluth, 8th coldest all-time 0.1 F at Crookston, 3rd coldest all-time -3.1 F at Roseau, 3rd coldest all-time 0.3 F at Park Rapids, 3rd coldest all-time -4.4 F at Embarrass, 2nd coldest all-time -4.1 F at Baudette, coldest all-time -3.7 F at Warroad, coldest all-time -2.9 F at Babbitt, coldest all-time -2.8 F at Gunflint Lake, coldest all-time In addition, some communities reported an exceptionally snowy month of December. -

The Change in Rainfall from Tropical Cyclones Due to Orographic Effect of the Sierra Madre Mountain Range in Luzon, Philippines
Philippine Journal of Science 145 (4): 313-326, December 2016 ISSN 0031 - 7683 Date Received: ?? Feb 20?? The Change in Rainfall from Tropical Cyclones Due to Orographic Effect of the Sierra Madre Mountain Range in Luzon, Philippines Bernard Alan B. Racoma1,2*, Carlos Primo C. David1, Irene A. Crisologo1, and Gerry Bagtasa3 1National Institute of Geological Sciences, College of Science, University of the Philippines, Diliman, Quezon City, Philippines 2Nationwide Operational Assessment of Hazards, University of the Philippines, Diliman, Quezon City, Philippines 3Institute of Environmental Science and Meteorology, College of Science, University of the Philippines, Diliman, Quezon City, Philippines This paper discusses the Sierra Madre Mountain Range of the Philippines and its associated influence on the intensity and distribution of rainfall during tropical cyclones. Based on Weather and Research Forecasting model simulations, a shift in rainfall was observed in different portions of the country, due to the reduction of the topography of the mountain. Besides increasing the rainfall along the mountain range, a shift in precipitation was observed during Tropical Storm Ondoy, Typhoon Labuyo, and Tropical Storm Mario. It was also observed that the presence of the Sierra Madre Mountain Range slows down the movement of a tropical cyclones, and as such allowing more time for precipitation to form over the country. Wind profiles also suggest that the windward and leeward sides of mountain ranges during Tropical Cyclones changes depending on the storm path. It has been suggested that in predicting the distribution of rainfall, the direction of movement of a tropical cyclones as well as its adjacent areas be taken into great consideration. -

Das Center for Disaster Managment and Risk Reduction Technology
Center for Disaster Management and Risk Reduction Technology CEDIM Forensic Disaster Analysis Group (FDA) TYPHOON 09W "RAMMASUN" – Short Summary 18 July 2014 – Report No. 1 – 12:00 GMT - Update: 30 July 2014 Authors: Bernhard Mühr, James Daniell, Tina Bessel, Susan Brink, Michael Kunz SUMMARY Official Disaster Name Date Landfall UTC Local Duration (PHL) Rammasun (Glenda, Philippines) 15/16-07 07 UTC +8 12 hours Rammasun (China, Vietnam) 18/19/20-07 06:30 UTC +8 12 hours Preferred Hazard Information: Definition (Saffir- Path Speed Simpson Scale) Width (km) Gust (Peak) Landfall Sustained 1st : Category 3 (15/7) 125 kt 15.07., 150 kph near WNW (Philippines) 20 kph Category 1 (16/7) Max: 150 232 kph 15 LT center 165 kt 135 kt Category 4 (18/7), Storm warning 306 kph 250 kph NW (China, Vietnam) 25 kph max. intensity 06 UTC area: 220 km (JTWC) (JTWC) Location Information: Provinces/ Economic Country ISO Regions Highest Impact Exposure HDI (2012) Urbanity Pop. affected Samar, Masbate, Philippines PH Luzon, Mindoro Not applicable 0.654 55% Ca. 2 million Hainan (including capital city Haikou, Hainan southern Guangdong Hanoi Area >10 million, CN Guangdong (Leizhou Peninsula), $321.1 billion Haikou 3.8 million China and and Guangxi south-eastern $563 billion 40.5 million people Vietnam VN Yunnan Guangxi USD PPP 0.617 potentially affected Vulnerability and Exposure Metrics (Population, Infrastructure, Economic) . 40.5 million people potentially affected in China (23 million) and Vietnam (18 million) . The total exposed value is $321.1 billion USD, or approx. $563 billion USD PPP (Purchasing Power Parity) In northern Vietnam, much less economic exposure (approx. -

Statistical Characteristics of the Response of Sea Surface Temperatures to Westward Typhoons in the South China Sea
remote sensing Article Statistical Characteristics of the Response of Sea Surface Temperatures to Westward Typhoons in the South China Sea Zhaoyue Ma 1, Yuanzhi Zhang 1,2,*, Renhao Wu 3 and Rong Na 4 1 School of Marine Science, Nanjing University of Information Science and Technology, Nanjing 210044, China; [email protected] 2 Institute of Asia-Pacific Studies, Faculty of Social Sciences, Chinese University of Hong Kong, Hong Kong 999777, China 3 School of Atmospheric Sciences, Sun Yat-Sen University and Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519082, China; [email protected] 4 College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao 266100, China; [email protected] * Correspondence: [email protected]; Tel.: +86-1888-885-3470 Abstract: The strong interaction between a typhoon and ocean air is one of the most important forms of typhoon and sea air interaction. In this paper, the daily mean sea surface temperature (SST) data of Advanced Microwave Scanning Radiometer for Earth Observation System (EOS) (AMSR-E) are used to analyze the reduction in SST caused by 30 westward typhoons from 1998 to 2018. The findings reveal that 20 typhoons exerted obvious SST cooling areas. Moreover, 97.5% of the cooling locations appeared near and on the right side of the path, while only one appeared on the left side of the path. The decrease in SST generally lasted 6–7 days. Over time, the cooling center continued to diffuse, and the SST gradually rose. The slope of the recovery curve was concentrated between 0.1 and 0.5. -

Disaster Response in Asia and the Pacific: a Guide to International Tools and Services (Hereafter Referred to As “The Guide”) Was Updated in 2017
DISASTER RESPONSE IN ASIA AND THE PACIFIC A Guide to International Tools and Services DISASTER RESPONSE IN ASIA AND THE PACIFIC A Guide to International Tools and Services Disaster Response in Asia and the Pacific TABLE OF CONTENTS I. INTRODUCTION . .2 II. GUIDANCE FRAMEWORKS. .8 A. Non-binding regulatory agreements between States . 9 B. Binding regulatory agreements between States . 11 C. Voluntary guidelines governing humanitarian action . .12 III. HUMANITARIAN ACTORS . 24 A. United Nations . 24 B. Red Cross and Red Crescent Movement. 25 C. Regional organizations and intergovernmental forums . 27 D. Non-governmental organizations . 33 E. Assisting Governments . 35 F. Foreign military assets . 37 G. Private sector. 37 IV. INTERNATIONAL COORDINATION MECHANISMS. .42 A. Global-level mechanisms . 43 B. Regional-level mechanisms . .47 C. Country-level mechanisms . .48 D. Coordinating actors . 51 V. TOOLS AND SERVICES . 58 A. Technical teams . .59 B. Relief assets and stockpiles . .73 C. Standby and surge rosters . 75 D. Information management. 81 E. Emergency response preparedness . 92 F. Humanitarian financing mechanisms. 99 VI. EARLY WARNING . 112 A. Early warning systems. .112 iv A Guide to International Tools and Services FIGURES Figure 1. How International and Regional Tools Support Disaster Response in Asia-Pacific . 3 Figure 2. Scope of the Guide: Response and Emergency Response Preparedness. 6 Figure 3. Humanitarian Principles. 8 Figure 4. Core Humanitarian Standard . 18 Figure 5. Regional Organizations and Intergovernmental Forums in Asia-Pacific . 31 Figure 6. Active Donors in Asia-Pacific . 36 Figure 7. Connecting Business Initiative National Hubs in Asia-Pacific . 39 Figure 8. IASC Humanitarian Leadership Structure . 44 Figure 9. -

Typhoon Risk in China: Wind Or Water? 中国的台风灾害: 是风还是雨?
Typhoon Risk in China: Wind or water? 中国的台风灾害: 是风还是雨? Margaret Joseph Model Product Management Typhoon Fitow, October 2013 台风菲特, 2013年10月 TYPHOON FITOW – RECORD BREAKING RAINFALL 台风菲特 - 破纪录的雨量 Landfall October 2013 登陆 2013 年10月 Category 2 at landfall 登陆时为第二级 ESCAP/WMO Typhoon Committee 8th Integrated Workshop: Member Report (2013) China ©2014 Risk Management Solutions, Inc. Confidential MY PICTURE TITLE Typhoon Fitow - Insured loss of ~USD1bn 台风菲特 - 约10亿美元的保险损失 www.news.cn Tropical Cyclone Precipitation Flooding 热带气旋降水驱动的洪水 Precipitation Model Rainfall-Runoff Model Riverine Surface Water 河流 地表水 Defence Model Defence Model Inundation Inundation ©2014 Risk Management Solutions, Inc. Confidential CAPTURING COMPLETE VIEW OF FLOOD RISK – RIVERINE AND SURFACE Riverine and WATER Riverine Surface Water Average Annual Loss Riverine 完整的模拟洪水 Surface Water 风险 河流和内涝 - Residual ©2014 Risk Management Solutions, Inc. Confidential Tropical Cyclone Precipitation Flooding 热带气旋降水驱动的洪水 Precipitation Model Rainfall-Runoff Model Riverine Surface Water 河流 地表水 Defence Model Defence Model Inundation Inundation ©2014 Risk Management Solutions, Inc. Confidential TYPHOON RAMMASUN 台风威马逊 Landfall July 2014 登陆 2014 年 7 月 Category 4 at landfall 登陆在第四类 Strongest typhoon landfall over Hainan in over 60 years 在60年内海南最强的 台风登陆 ©2014 Risk Management Solutions, Inc. Confidential MODELLING TYPHOON RAMMASUN 模拟台风威 马逊 ©2014 Risk Management Solutions, Inc. Confidential TYPHOON RAMMASUN 台风威马逊 Landfall July 2014 登陆 2014 年 7 月 Category 4 at landfall 登陆在第四类 Strongest typhoon landfall over Hainan in over 60 years 在60年内海南最强的 台风登陆 http://english.caixin.com/ ©2014 Risk Management Solutions, Inc. Confidential Storm Surge Flooding Tropical Cyclone Precipitation Flooding STORM SURGE Precipitation Model MODELLING Storm Surge Model Rainfall-Runoff Model 风暴潮模拟 The (typhoon) flood model Riverine Surface Water combines inland (tropical 河流 地表水 cyclone precipitation driven) and coastal (surge driven) risk). -

Philippines 2013 / Typhoon Haiyan
ASIA - PACIFIC A.8 / PHILIPHILIPPINES 2013-2016 / TYPHOON HAIYAN OVERVIEW NATURAL DISASTER OVERVIEW PHILIPPINES 2013 / TYPHOON HAIYAN CRISIS Typhoon Haiyan (Yolanda), 8 November 2013. TOTAL HOUSES 1,012,790 houses (518,878 partially dam- DAMAGED1 aged and 493,912 totally destroyed). MANILA TOTAL PEOPLE 2 households (16,078,181 persons). BICOL AFFECTED 3,424,593 REGION MIMAROPA 3 TYPHOON HAIYAN EASTERN RESPONSE OUTPUTS WESTERN VISAYAS National Housing 29,661 houses as of October 2016 (206,488 planned). VISAYAS Authority (NHA) CENTRAL VISAYAS NEGROS Department of Social CARAGA Welfare and Develop- cash transfers and material vouchers distributed. ment (DSWD) 966,341 551,993 households assisted with emergency shelter. Humanitarian organizations 497,479 NFI packages distributed. MALAYSIA households assisted with incremental solutions. Map highlighting the path of typhoon Haiyan and the most 344,853 affected regions, including: Eastern Visayas: Biliran, Leyte, Southern Leyte, Samar, Northern Samar, Eastern Samar. 1 Philippines Shelter Cluster, late 2014, Analysis of Shelter Recovery, http://bit.ly/2kZgHvA. Central Visayas: Cebu, Bohol. Negros: Negros Occidental, 2 National Disaster Risk Reduction and Management Council (NDRRMC), Update 17 April 2014, Negros Oriental. Western Visayas: Aklan, Capiz, Iloilo, An- http://bit.ly/1B6MMl1. tique, Guimaras. Mimaropa: Palawan, Occidental Mindoro, 3 Sources for these figures are the documents used as references throughout this overview. Oriental Mindoro, Romblon. Bicol Region: Masbate, Sorso- gon. Caraga: Dinagar Islands, Surigao del Norte, Camiguin. SUMMARY OF THE RESPONSE RIO NAPO Super Typhoon Haiyan (Yolanda) made landfall on 8 November 2013 and was one of the largest typhoons ever recorded. While the main government response consisted of subsidies for housing reconstruction or repair, humanitarian agencies used a range of approaches which included cash- or voucher-based interventions, but also training and construction of transitional, core or permanent shelters. -

Valuing Protective Services of Mangroves in the Philippines Technical Report
WAVES Technical Report July 2017 Valuing Protective Services of Mangroves in the Philippines Technical Report Wealth Accounting and the Valuation of Ecosystem Services i www.wavespartnership.org Team at the Institute of Hydraulics at the University of Cantabria ÍÑIGO J. LOSADA RODRÍGUEZ PELAYO MENÉNDEZ FERNÁNDEZ ANTONIO ESPEJO HERMOSA SAÚL TORRES ORTEGA PEDRO DÍAZ SIMAL FELIPE FERNÁNDEZ PÉREZ SHEILA ABAD HERRERO NICOLÁS RIPOLL CABARGA JAVIER GARCÍA ALBA Team at The Nature Conservancy MICHAEL W. BECK SIDDHARTH NARAYAN DANIA TRESPALACIOS ANGELA QUIROZ This Technical Report was primarily funded by World Bank WAVES program. Additional funding was provided by the International Climate Initiative (IKI) of the German Federal Ministry for the Environment, Nature Conservation, Building and Nuclear Safety (BMUB), and the Lloyd’s Tercentenary Research Foundation. This Technical Report is accompanied by a Policy Brief for policy makers. Many thanks to Stefanie Sieber, Glenn-Marie Lange, Maya Gabriela Q. Villaluz, Gem Castillo, Rosalyn Sontillanosa, Marnel Ratio and to the attendees of the Valuation training the week of Dec 5, 2016. Suggested Citation: Losada, I.J., M. Beck, P. Menéndez, A. Espejo, S. Torres, P. Díaz-Simal, F. Fernández, S. Abad, N. Ripoll, J. García, S. Narayan, D. Trespalacios. 2017. Valuation of the Coastal Protection Services of Mangroves in the Philippines. World Bank, Washington, DC. Points of contact: Michael W. Beck, [email protected] Íñigo J. Losada Rodríguez, [email protected] WAVES - Global Partnership for Wealth Accounting and the Valuation of Ecosystem Services Wealth Accounting and the Valuation of Ecosystem Services (WAVES) is a global partnership led by the World Bank that aims to promote sustainable development by mainstreaming natural capital in development planning and national economic accounting systems, based on the System of Environmental-Economic Accounting (SEEA). -

Disaster Risk Financing a Global Survey of Practices and Challenges
Disaster Risk Financing A GLOBAL SURVEY OF PraCTICES AND CHALLENGES Contents Executive summary Chapter 1. Financial management of disaster risks Disaster Risk Financing Chapter 2. Assessment of disaster risks, financial vulnerabilities and the impact of disasters A GLOBAL SURVEY OF PraCTICES Chapter 3. Private disaster risk financing tools and markets and the need for financial preparedness AND CHALLENGES Chapter 4. Government compensation, financial assistance arrangements and sovereign risk financing strategies Chapter 5. Key priorities for strengthening financial resilience Disaster Risk Financing Financing Risk Disaster A GLOB A L SU R VEY O F P ra CTICES A N D CH A LLENGES Consult this publication on line at http://dx.doi.org/10.1787/9789264234246-en. This work is published on the OECD iLibrary, which gathers all OECD books, periodicals and statistical databases. Visit www.oecd-ilibrary.org for more information. ISBN 978-92-64-23423-9 21 2015 02 1 P Disaster Risk Financing A GLOBAL SURVEY OF PRACTICES AND CHALLENGES This work is published on the responsibility of the Secretary-General of the OECD. The opinions expressed and arguments employed herein do not necessarily reflect the official views of the Organisation or of the governments of its member countries. This document and any map included herein are without prejudice to the status of or sovereignty over any territory, to the delimitation of international frontiers and boundaries and to the name of any territory, city or area. Please cite this publication as: OECD (2015), Disaster Risk Financing: A global survey of practices and challenges, OECD Publishing, Paris. http://dx.doi.org/10.1787/9789264234246-en ISBN 978-92-64-23423-9 (print) ISBN 978-92-64-23424-6 (PDF) The statistical data for Israel are supplied by and under the responsibility of the relevant Israeli authorities. -

2008 Tropical Cyclone Review Summarises Last Year’S Global Tropical Cyclone Activity and the Impact of the More Significant Cyclones After Landfall
2008 Tropical Cyclone 09 Review TWO THOUSAND NINE Table of Contents EXECUTIVE SUMMARY 1 NORTH ATLANTIC BASIN 2 Verification of 2008 Atlantic Basin Tropical Cyclone Forecasts 3 Tropical Cyclones Making US Landfall in 2008 4 Significant North Atlantic Tropical Cyclones in 2008 5 Atlantic Basin Tropical Cyclone Forecasts for 2009 15 NORTHWEST PACIFIC 17 Verification of 2008 Northwest Pacific Basin Tropical Cyclone Forecasts 19 Significant Northwest Pacific Tropical Cyclones in 2008 20 Northwest Pacific Basin Tropical Cyclone Forecasts for 2009 24 NORTHEAST PACIFIC 25 Significant Northeast Pacific Tropical Cyclones in 2008 26 NORTH INDIAN OCEAN 28 Significant North Indian Tropical Cyclones in 2008 28 AUSTRALIAN BASIN 30 Australian Region Tropical Cyclone Forecasts for 2009/2010 31 Glossary of terms 32 FOR FURTHER DETAILS, PLEASE CONTACT [email protected], OR GO TO OUR CAT CENTRAL WEBSITE AT HTTP://WWW.GUYCARP.COM/PORTAL/EXTRANET/INSIGHTS/CATCENTRAL.HTML Tropical Cyclone Report 2008 Guy Carpenter ■ 1 Executive Summary The 2008 Tropical Cyclone Review summarises last year’s global tropical cyclone activity and the impact of the more significant cyclones after landfall. Tropical 1 cyclone activity is reviewed by oceanic basin, covering those that developed in the North Atlantic, Northwest Pacific, Northeast Pacific, North Indian Ocean and Australia. This report includes estimates of the economic and insured losses sus- tained from each cyclone (where possible). Predictions of tropical cyclone activity for the 2009 season are given per oceanic basin when permitted by available data. In the North Atlantic, 16 tropical storms formed during the 2008 season, compared to the 1950 to 2007 average of 9.7,1 an increase of 65 percent.