Single Snapshot System for the Fast 3D Modeling Using Dynamic Time Warping
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Free Tools Photosynth
Free Tools Photosynth Making a Photosynth Creating the best synth starts with the right photos. Here are some key tips: • Take overlapping panoramas from different locations • Have lots of overlap between shots to get good matching • Limit the angles between photos (no more than 25 degrees – at least 15 per full rotation) • Pick scenes or objects with lots of detail and texture • Don’t crop your images before synthing • Rotate your photos to be ‘up’ correctly before synthing Once you have signed in, click the Upload button (top right of page) or click on the Create your Synth icon on the home page. (scroll down). If you do not have the software you will be prompted to download it first. Once it is installed you will see the Create a Synth button. You will see a pop-up window with Start a new synth button. Give your synth a name, tags (descriptive words) and description. Click Add Photos, browse to your files add them. Then click on the Synth button at the bottom of the page. Photosynth will do the rest for you. Making a Panorama Many photosynths consist of photos shot from a single location. Our friends in Microsoft Research have developed a free, world class panoramic image stitcher called Microsoft Image Composite Editor (ICE for short.) ICE takes a set of overlapping photographs of a scene shot from a single camera location, and creates a single high-resolution image. Photosynth now has support for uploading, exploring and viewing ICE panoramas alongside normal synths. Here’s how to create a panorama in ICE and upload it to Photosynth: 1. -
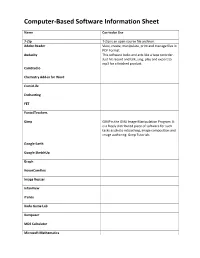
Computer-Based Software Information Sheet
Computer-Based Software Information Sheet Name Curricular Use 7-Zip 7-Zip is an open source file archiver. Adobe Reader View, create, manipulate, print and manage files in PDF Format Audacity This software looks and acts like a tape recorder. Just hit record and talk, sing, play and export to mp3 for a finished product. CamStudio Chemistry Add-in for Word ComicLife Enchanting FET Fonts4Teachers Gimp GIMP is the GNU Image Manipulation Program. It is a freely distributed piece of software for such tasks as photo retouching, image composition and image authoring. Gimp Tutorials Google Earth Google SketchUp Graph HoverCamFlex Image Resizer InfanView iTunes Kodu Game Lab Komposer MDS Calculator Microsoft Mathematics Microsoft Office Mp4Cam2Avi This software is to convert Mp4 video files from a camera to an Avi video file. MuseScore Paint.NET Paint.NET is free image editing and photo manipulation software. It features an intuitive and innovative user interface with support for layers, unlimited undo, special effects, and a wide variety of useful and powerful tools. Paint.NET Tutorials. Photo Story Microsoft Photo Story is a free application that allows users to create a visual story (show and tell presentation) from their digital photos. Photosynth Pivot Stickfigure Animator Pivot makes it easy to create stick-figure animations. You can build your own stick figures and load your own backgrounds. The animations can be saved as animated gifs to be used on web pages. Scratch Songsmith SMART Education Software (Notebook) SMART Ideas StoryBoardPC VirtualDub Windows Movie Maker WinScp Zoomit . -

Developing a Zoomable Timeline for Big History
19 From Concept to Reality: Developing a Zoomable Timeline for Big History Roland Saekow Abstract Big History is proving to be an excellent framework for designing undergradu- ate synthesis courses. A serious problem in teaching such courses is how to convey the vast stretches of time from the Big Bang, 13.7 billion years ago, to the present, and how to clarify the wildly different time scales of cosmic history, Earth and life history, human prehistory and human history. Inspired by a se- ries of printable timelines created by Professor Walter Alvarez at the Univer- sity of California, Berkeley, a time visualization tool called ‘ChronoZoom’ was developed through a collaborative effort of the Department of Earth and Plane- tary Science at UC Berkeley and Microsoft Research. With the help of the Of- fice of Intellectual Property and Industry Research Alliances at UC Berkeley, a relationship was established that resulted in the creation of a prototype of ChronoZoom, leveraging Microsoft Seadragon zoom technology. Work on a sec- ond version of ChronoZoom is presently underway with the hope that it will be among the first in a new generation of tools to enhance the study of Big History. In Spring of 2009, I had the good fortune of taking Walter Alvarez' Big His- tory course at the University of California Berkeley. As a senior about to com- plete an interdisciplinary degree in Design, I was always attracted to big picture courses rather than those that focused on specifics. So when a housemate told me about Walter's Big History course, I immediately enrolled. -

3D-Models of the Human Habitat for the Internet
3D-MODELS OF THE HUMAN HABITAT FOR THE INTERNET Franz Leberl Institute of Computer Graphics and Vision, Graz University of Technology, Graz, Austria Michael Gruber Microsoft Photogrammetry, Graz, Austria Keywords: Internet, Geo-data, Photogrammetry, 3-dimensional objects. Abstract: The Internet has inspired an enormous appetite for 3-dimensional geo-data of the urban environment to support location-aware applications. This has in fact become the surprising „killer application“ of such 3- dimensional data. In March 2005, at the occasion of his 50th birthday, Bill Gates went public with his “Virtual Earth Vision” for local search in the Internet and stated: "You'll be walking around in downtown London and be able to see the shops, the stores, see what the traffic is like. Walk in a shop and navigate the merchandise. Not in the flat, 2D interface that we have on the web today, but in a virtual reality walkthrough.” The key words are „walk in a shop“. This implies the need for an enormous detail, and the associated computing power, communications bandwidth, miniaturization of computing, increase of storage capacity and in the ability to model the human habitat (the Earth) in great detail in 3 dimensions. This paper seeks to evangelize the current capabilities of the Virtual Earth system, focuses on the creation of 3D data, but also points to some pieces of new science in the 3D-analysis of overlapping imagery of the human habitat at sub-pixel accuracies 1 FROM 2-DIMENSIONAL oftentimes on the basis of an existing telephone directory business. Under NAVIGATION TO http://www.klicktel.de/routenplaner/ one finds one 3-DIMENSIONAL SEARCH sample solution for Germany. -

How to View Panoramic Photos on Pc Free Download How to View Panoramic Photos on Pc Free Download
how to view panoramic photos on pc free download How to view panoramic photos on pc free download. Today's digital cameras and even smartphones provide pictures with a resolution that is far beyond the capabilities of computer monitors. Find out what's really inside your pictures! Check out the free Panorado viewer! See the whole of it! When you look at a panorama, you are right in the center of a virtual location. Panoramic images can be easily created from camera or smartphone shots. With the Panorado viewer, you'll get them on your computer screen! Panorado 5.0. is a comfortable image viewer, browser, and organizer for Windows. Find out more about Panorado 5.0! See a larger demo! Download and test it! [Win32] [Win64] Panorado JS 2.5. is the state-of-the-art HTML5 image viewer for websites and web applications. How to view panoramic photos on pc free download. Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. What can I do to prevent this in the future? If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. -

Geometry Directed Browser for Personal Photographs
Geometry Directed Browser for Personal Photographs ∗ Aditya Deshpande Siddharth Choudhary P J Narayanan Krishna Kumar Singh Kaustav Kundu Aditya Singh Apurva Kumar Center for Visual Information Technology International Institute of Information Technology Hyderabad, India ABSTRACT phers to watch the pictures again. Photo browsers, however, Browsers of personal digital photographs all essentially fol- follow the model of presenting the collection of photographs low the slide show paradigm, sequencing through the pho- linearly in the order in which photos were taken, usually in tos in the order they are taken. A more engaging way to a slide show mode. This model has practically not changed browse personal photographs, especially of a large space like from the early days of digital photography, though there a popular monument, should involve the geometric context has been drastic changes in how humans interact with other of the space. In this paper, we present a geometry directed digital data. The photo sharing sites like Flickr, Picasa, photo browser that enables users to browse their personal and Facebook, also provide similar browsing mechanisms, pictures with the underlying geometry of the space to guide but enable one to share the photographs with a larger circle the process. The browser uses a pre-computed package of of people easily. Some tools have started to use the con- geometric information about the monument for this task. tent in the photographs, for example, Zhang et al. perform The package is used to register a set of photographs taken automated annotation of family albums using a Bayesian by the user with the common geometric space of the monu- framework to model the similarity of faces [15], Davis et al. -

Canada Teacher Awar Canada Innovative Teacher Awards 2012 Innovative R Awards
CANADA INNOVATIVE TEACHER AWARDS 2012 Program Overview and Guidelines 1 TABLE OF CONTENTS 1. Introduction …………………………………………………………………………………3 2. Canada Innovative Teacher Awards & World Wide Global Forum Overview……….4 3. Microsoft Software and Tools for Canada Innovative Teacher Awards Projects………………………………………………5 4. Procedures, Guidelines and Timelines…………………………………………………..6 • Section 1: Create Your Learning Project Video/Criteria • Section 2: Submit Video Learning Activity Application Form 5. Partners in Learning Canada Virtual Innovative Educator Forum Overview:……….9 Virtual Competition for Canada Innovative Teacher Awards • Video Learning Activity Selection Process • Steps/Guidelines for Selected Participants 6. APPENDIX ‘A’: Judging Rubric…………………………………………………………10 7. APPENDIX ‘B’: Instructions to Upload VCT/Learning Activity………………………16 8. APPENDIX ‘C’: Video Learning Activity Application Form…………………………..20 2 1. Introduction About Microsoft in Education http://www.microsoft.com/education/ww/about/Pages/index.aspx An educated population is the one natural resource that increases in value as it increases in size. Microsoft’s mission in education is to help every student and educator around the world realize their full potential by helping educators and school leaders connect, collaborate, create, and share so that students can realize their greatest potential. We do this by building capacity, growing learning communities and expanding teaching and learning through our Partners in Learning Program. Microsoft Partners in Learning Vision Microsoft Partners in Learning is a global initiative designed to actively increase access to technology and improve its use in learning. At Microsoft, we are deeply committed to working with governments, communities, schools, and educators to use the power of information technology to deliver technology, services, and programs that provide anytime, anywhere learning for all. -

Ways with Free Tools Creative What an Exciting Time to Be a Teacher
Engage your students in ways with free tools creative What an exciting time to be a teacher. Students are more aware of the world, eager to embrace new ideas and try new technologies. To help, Microsoft® has lots of free tools to help you engage your students and energize a lesson plan. FREE TOOLS 1 Motivate. Create. Share. Microsoft® offers free tools and technologies to help you motivate and captivate your students. Included in the collection are interactive activities that can inspire students to explore as a group or as individuals for their own personal learning. Ask students to gather images from the Web or snap their own photos on a subject. Then create a compelling piece of art with AutoCollage, the free collage-making photo tool from Microsoft. Top 3 reasons to consider 1. They’re free 2. Personal discovery 3. Student and teacher-friendly Today, most every school is faced These free tools from Microsoft These tools are free and easy to free tools with budget challenges. Having can help motivate students to download from a Web browser. tools available of this high quality express their creativity or achieve For the most part, they don’t and interactivity is a great un- personal success in an area that require special training, so you tapped resource for teachers. truly interests them. From art to can explain or use them quickly music to science, these free tools and engage your class in a pro- have something to offer students ductive learning activity. in nearly every grade. FREE tools 2 Engage with multimedia It’s a Web surfing, clicking, high definition world we inhabit. -

Title Stuff Here
Pixel Nation 80 Weeks of World Wide Wade by Wade Roush Xconomy.com Pixel Nation: 80 Weeks of World Wide Wade by Wade Roush Copyright © 2008-2010 Xconomy Inc. All Rights Reserved Published by Xconomy (www.xconomy.com). No part of this book may be used or reproduced in any manner whatsoever without written permission except in the case of brief quotations embodied in critical articles or reviews. To inquire about reproduction or to report errors, please e-mail: [email protected]. All product names and registered trademarks used in this book are the property of their respective owners. Cover photo by Wade Roush. Contents Introduction 1: Reinventing Our Visual World, Pixel By Pixel 2: The Coolest Tools for Trawling & Tracking the Web 3: Google Earth Grows a New Crop of 3-D Buildings, and Other Web Morsels to Savor 4: Turn Your HDTV into a Digital Art Canvas 5: Unbuilt Boston: The Ghost Cloverleaf of Canton 6: An Elegy for the Multimedia CD-ROM Stars 7: The Future‘s So Bright, I Gotta Wear Screens 8: Science Below the Surface 9: Gazing Through Microsoft‘s WorldWide Telescope 10: Megapixels, Shmegapixels: How to Make Great Gigapixel Images With Your Humble Digital Camera 11: You Say Staccato, I Say Sfumato: A Reply to Nicholas Carr 12: Space Needle Envy: A Bostonian‘s Ode to Seattle 13: You‘re Listening to Radio Lab—Or You Should Be 14: Can Evernote Make You into a Digital Leonardo? 15: Are You Ready to Give Up Cable TV for Internet Video? 16: Turn your iPhone or iPod into a Portable University 17: In Defense of the Endangered Tree Octopus, and Other Web Myths 18: Pogue on the iPhone 3G: A Product Manual You Won‘t Be Able to Put Down 19: Photographing Spaces, Not Scenes, with Microsoft‘s Photosynth 20: What Web Journalists Can Learn from Comics 21: ZvBox‘s Unhappy Marriage of PC and HDTV 22: GPS Treasure Hunting with Your iPhone 3G 23: Boston Unblurred: Debunking the Google Maps Censorship Myth 24: Four Ways Amazon Could Make Kindle 2.0 a Best Seller 25: Playful vs. -

Microsoft IT Academy Report Template
Free Education Resources from Microsoft Microsoft has several websites that offer education resources for anyone who wants to help students with homework or get them interested in computer technology. Microsoft Virtual Academy Improve your IT skill set and help advance your career with a free, easy to access training portal. Learn at your own pace, focusing on Microsoft technologies, gain points and get recognition. Visit http://www.microsoftvirtualacademy.com/Home.aspx to find out more. Shout Shout is a multiyear global education initiative offering webinars and projects for both educators and students. Visit http://shoutlearning.org/index.html to find out more. Digital Literacy Whether you are new to computing or have some experience, this curriculum will help you develop a fundamental understanding of computers. The courses help you learn the essential skills to begin computing with confidence, be more productive at home and at work, stay safe online, use technology to complement your lifestyle, and consider careers where you can put your skills to work. Visit http://www.microsoft.com/digitalliteracy to find out more. Microsoft Education The mission of Microsoft’s education efforts is to help students and educators throughout the world realize their full potential. The education website offers free classroom and teacher resources like lesson plans and tutorials. Visit http://www.microsoft.com/education to find out more. Microsoft offers free tools to help engage students in a variety of subject areas—from movie-making to collaboration to science and beyond. Teachers can download these tools for free, the majority of which require no special training. -
Utilization of Photosynth Point Clouds for 3D Object Reconstruction
22nd CIPA Symposium, October 11-15, 2009, Kyoto, Japan Utilization of Photosynth Point Clouds for 3D Object Reconstruction Guenter Pomaska University of Applied Sciences Bielefeld, Faculty for Civil Engineering and Architecture, Germany [email protected] KEY WORDS: 3D, Acquisition, CAD, Monument, Object Reconstruction, Virtual Reality ABSTRACT: There is a growing demand in modeling amorphous shapes like statues, figurine or monuments for computer visualization and documentation. Using photographs as the data source is a most convenient recording mode on site. The equipment is easy to handle and transportation is in no case a problem as it can occur if a laser scanning device has to be employed. A photograph is a container of high information density. It carries radiometric information and can provide range values as well. In terms of computer vision, structure from motion is a process to find the correspondence between images. Features must be tracked from one image to the next. The 3D positions of the feature points and the camera movement is the result of the registration process. In the cultural heritage community the Epoch ARC 3D Web service is in common use. Linked with the open source tool MeshLab it provides an automated workflow including object reconstruction, mesh processing and textured rendering. Recent developments from Microsoft introduce photo browsing. The Web community can view images from cities in Virtual Earth and participate with own objects applying Photosynth. Photosynth is designed as an image browser for objects, documented by internet imagery. The user navigates through a bundle of images representing the object. A smooth transition from one photo to the next is leading to the impression of a 3D model. -

The Thing About Bing
ARTICLE HYDRO INTERNATIONAL INTERVIEWS CHRIS PENDLETON The Thing about Bing Bing Maps users will soon be able to look skyward from Streetside and see the stars and constellations. That is just one of the ways in which the Bing Maps team is creating what may turn out to be the coolest mapping technology yet. In the meantime, thousands of organisations and developers around the world are delivering rich imagery through the maps APIs and other technology from Bing Maps, the web mapping service that is part of the Bing suite of search engines. We caught up with Chris Pendleton, the Bing Maps technical evangelist for Microsoft, to find out more about the technology and specific uses for hydrographers and oceanographers in Bing. What does your job entail? As the Bing Maps technical evangelist, I educate users on using Bing Maps in both our consumer and platform experiences. Whether it's by writing posts on my Bing Maps blog, speaking at conferences or producing videos with industry experts, I find a way to increase the use of mapping in our everyday lives. How did you get into this field? After completing my undergraduate studies I took a web developer position with a small start-up called NetCreate Systems in San Diego. NetCreate built custom websites from the ground up and featured clients such as Intuit, TheScientist.com and AICPA.org. NetCreate also evolved a template-based website creation tool for enterprises, which attracted the likes of Ace Hardware, Herbalife and Shell Oil, to name a few. NetCreate was acquired by Vicinity Corporation, which focused on building store locators.