DOCSLIB.ORG

The Volatility Structure Implied by Options on the SPI Futures Contract by Christine A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Volatility Structure Implied by Options on the SPI Futures Contract by Christine A 2 The Volatility Structure Implied by Options on the SPI Futures Contract by Christine A. Brown † Abstract: The Asay (1982) option pricing model prices options on futures contracts where the premia are margined. The model assumes that the volatility of the underlying futures contract is constant over the life of the option. However it is an empirical observation in many markets that options on the same underlying futures contract with the same maturity, but at different strikes, trade at different implied volatilities. Since the 1987 crash, it has been documented that in many markets the volatility implied by out-of-the-money put options is higher than that implied by out-of-the-money call options. This phenomenon has become known as the ‘volatility skew’. This paper examines the volatility structure for options on the SPI futures contract over the period June 1993 to June 1994, and provides theoretical explanations consistent with its shape. Keywords: ASAY MODEL; VOLATILITY SMILE; VOLATILITY SKEW. † Department of Accounting and Finance, University of Melbourne, Parkville, Victoria 3052. Email: [email protected] I am grateful to Rob Brown, Kevin Davis and James Pickles for helpful comments, and to Raymond Liu for research assistance. Australian Journal of Management, Vol. 24, No. 2, December 1999, © The Australian Graduate School of Management – 115– AUSTRALIAN JOURNAL OF MANAGEMENT December 1999 1. Introduction he Sydney Futures Exchange (SFE) is one of the few futures exchanges to trade Toptions on futures where the options are subject to futures style margining.1 An initial margin2 is deposited and the option contract is marked to market at the end of each day, where the loss on a long option position is limited to the size of the initial premium. The margining applied to options traded on the SFE implies that option pricing models, developed for the situation where option premia are paid up front, are inappropriate. The standard option pricing model used to price options on futures contracts is the Black (1976) model for pricing options on commodity futures. Asay (1982) and Lieu (1990) have modified the Black (1976) model,3 to account for the daily margining of the option contract. Using the Asay model the call premium, C, for a European option on the underlying futures, F, satisfies: C = FN(d1) – XN(d2), (1) ln (FX/t ) + 1σ 2 where : d1 = 2 , σ t d2 = d1 – σ√t, and F = futures price; X = exercise price; C = call price; t = time to maturity; and σ = instantaneous volatility. The put premium, P, is given by: P = XN(–d2) – FN(–d1) (2) The model given by equations 1 and 2 is similar to Black’s (1976) model for pricing options on commodity futures, the difference being the absence of the interest rate term in the above equations. Therefore the price of an option where the premium is margined, relative to one where the premium is paid up front, will be higher. When the option premium is paid up front the buyer is committing funds and the writer receives those funds, while for options which are margined the option premium no longer flows from the buyer to the writer. It can be shown that under certain conditions it is optimal to exercise a put option early when the premium is charged up front. The Black and Scholes (1973) model and the Black (1976) model which are developed for European options are 1. Another exchange which also margins its futures options is the LIFFE. 2. The SFE introduced the SPAN margining system in 1994. This system accounts for the overall risk of a position (containing futures and options on the SPI) as both the futures price moves and the volatility changes. 3. This modified model will be referred to as the Asay model throughout the paper. –116– Vol. 24, No. 2 Brown: VOLATILITY STRUCTURE IMPLIED BY OPTIONS not immediately applicable to pricing American options because these models do not price the early exercise flexibility of American put options (or American call options where the underlying asset pays a dividend).4 However, Lieu (1990) shows that under futures-style margining it is never optimal to exercise a call option or a put option early, and therefore the model given by equations 1 and 2 above applies to the American style options on the Share Price Index (SPI) futures contract traded on the SFE. The assumptions underpinning the Asay (1982) model are the same as for the Black (1976) and the Black and Scholes (1973) models. The underlying futures price is assumed to be lognormally distributed, markets are assumed to be frictionless with trading taking place continuously, and the short term interest rate is assumed to be known with certainty. The process that drives changes in the futures price is assumed to have two components: an expected drift rate and an uncertain or stochastic component scaled by the volatility parameter, which is assumed constant over the life of the option. In practice, the volatility parameter is the only unobservable parameter in the model. Because the option price, the futures price, time to maturity, interest rate and strike price are all observable (or measurable), we can substitute these parameters into the equations, and solve for the only unknown parameter, volatility.5 This volatility derived from the known parameters is called the implied volatility and is obtained by backing the volatility out of equations 1 and 2. Using this procedure to solve for an implied volatility assumes that market participants are using the Asay model to price options. If the model were correctly specified and all its assumptions valid, then the implied volatility for all options (observed at the same time) with the same maturity but different strikes, should be equal. Indeed, under the assumption that the market for stock index futures options is efficient then empirical observation of implied volatility varying across strike prices, contrasts the option valuation with the Black (1976) or the Asay (1982) formulae. In many markets prior to the 1987 stock market crash, there appeared to be a symmetry around the zero moneyness, where out-of-the-money and in-the-money options traded at higher implied volatilities than the implied volatilities for at-the- money options. This dependence of implied volatility on the strike, for a given maturity became known as the smile effect, although the exact structure of volatility varied across markets and even within a particular market from day to day. However, since the 1987 stock market crash the smile has changed shape in many markets, particularly for traded options on stock indexes, where the function has gone from a smile shape to more of a ‘sneer’. The idea of the volatility ‘smile’ had its genesis in the early papers documenting the systematic pricing biases of the Black and Scholes (1973) option pricing model. Black (1975) suggests that the non-stationary behaviour of volatility would lead the Black-Scholes model to overprice or underprice options. Other authors have confirmed the existence of systematic biases in the model.6 4. It may be optimal to exercise an American call option just prior to a dividend payment. Merton (1973) shows that this will not occur in theory but it could occur in practice due to factors outside the option pricing model. 5. This requires a numerical search procedure because the equations are not immediately solvable for volatility. 6. See, for example, Macbeth and Merville (1979), Whaley (1982), Emanuel and Macbeth (1982), Rubinstein (1985), Brown and Taylor (1997). – 117 – AUSTRALIAN JOURNAL OF MANAGEMENT December 1999 Following Heynen, Kemna and Vorst (1994), explaining the implied volatility structure may lead to the conclusion that option prices are better described by an alternative underlying asset price process. Taylor and Xu (1993) study the smile effect of implied volatilities and show that the existence of stochastic volatility is a sufficient reason for smiles to exist. They show that an approximation to the theoretical implied volatility is a quadratic function of ln(F/X) where F is the forward price and X is the strike price, and that this approximate function has a minimum when X = F. This theoretical result requires that asset price and volatility differentials are uncorrelated and that volatility risk is not priced. Using currency option data obtained from the Philadelphia Stock Exchange, over the period from 1984 to 1992, and regressing a function of theoretical and observed implied volatilities on moneyness, they find little evidence of asymmetry in implied volatilities. However, the empirical smile pattern is about twice the size predicted by the theory. Figure 1 Implied Volatility Smiles for German Mark/USD Call Options (adapted from Xu & Taylor (1993)) 2 1.5 1 10-Day 30-Day 0.5 Implied Volatility Ratio 0 -0.1 -0.05 0 0.05 0.1 Moneyness Figure 1 reproduces the nature of the volatility smile for foreign exchange options as presented by Taylor and Xu (1993). On the vertical axis the ratio is the implied volatility at the relevant strike divided by the implied volatility when the strike price is exactly equal to the forward price of the currency.7 Thus, a ratio of 1.5 for a 5% out-of-the-money option implies that the out-of-the-money option has an implied volatility that is 1.5 times the implied volatility of an at-the-money option. Shastri and Wethyavivorn (1987) find similar results for foreign currency options traded in 1983 and 1984, while Sheik (1991) has argued that a similar pattern occurred for S&P 500 options during 1983 to 1985. 7. Because it may not be possible to observe an option trading exactly at-the-money Xu and Taylor (1994) give a method to estimate the at-the-money implied volatility.
Load more

Recommended publications
  • Section 1256 and Foreign Currency Derivatives
    Section 1256 and Foreign Currency Derivatives Viva Hammer1 Mark-to-market taxation was considered “a fundamental departure from the concept of income realization in the U.S. tax law”2 when it was introduced in 1981. Congress was only game to propose the concept because of rampant “straddle” shelters that were undermining the U.S. tax system and commodities derivatives markets. Early in tax history, the Supreme Court articulated the realization principle as a Constitutional limitation on Congress’ taxing power. But in 1981, lawmakers makers felt confident imposing mark-to-market on exchange traded futures contracts because of the exchanges’ system of variation margin. However, when in 1982 non-exchange foreign currency traders asked to come within the ambit of mark-to-market taxation, Congress acceded to their demands even though this market had no equivalent to variation margin. This opportunistic rather than policy-driven history has spawned a great debate amongst tax practitioners as to the scope of the mark-to-market rule governing foreign currency contracts. Several recent cases have added fuel to the debate. The Straddle Shelters of the 1970s Straddle shelters were developed to exploit several structural flaws in the U.S. tax system: (1) the vast gulf between ordinary income tax rate (maximum 70%) and long term capital gain rate (28%), (2) the arbitrary distinction between capital gain and ordinary income, making it relatively easy to convert one to the other, and (3) the non- economic tax treatment of derivative contracts. Straddle shelters were so pervasive that in 1978 it was estimated that more than 75% of the open interest in silver futures were entered into to accommodate tax straddles and demand for U.S.
    [Show full text]
  • Buying Options on Futures Contracts. a Guide to Uses
    NATIONAL FUTURES ASSOCIATION Buying Options on Futures Contracts A Guide to Uses and Risks Table of Contents 4 Introduction 6 Part One: The Vocabulary of Options Trading 10 Part Two: The Arithmetic of Option Premiums 10 Intrinsic Value 10 Time Value 12 Part Three: The Mechanics of Buying and Writing Options 12 Commission Charges 13 Leverage 13 The First Step: Calculate the Break-Even Price 15 Factors Affecting the Choice of an Option 18 After You Buy an Option: What Then? 21 Who Writes Options and Why 22 Risk Caution 23 Part Four: A Pre-Investment Checklist 25 NFA Information and Resources Buying Options on Futures Contracts: A Guide to Uses and Risks National Futures Association is a Congressionally authorized self- regulatory organization of the United States futures industry. Its mission is to provide innovative regulatory pro- grams and services that ensure futures industry integrity, protect market par- ticipants and help NFA Members meet their regulatory responsibilities. This booklet has been prepared as a part of NFA’s continuing public educa- tion efforts to provide information about the futures industry to potential investors. Disclaimer: This brochure only discusses the most common type of commodity options traded in the U.S.—options on futures contracts traded on a regulated exchange and exercisable at any time before they expire. If you are considering trading options on the underlying commodity itself or options that can only be exercised at or near their expiration date, ask your broker for more information. 3 Introduction Although futures contracts have been traded on U.S. exchanges since 1865, options on futures contracts were not introduced until 1982.
    [Show full text]
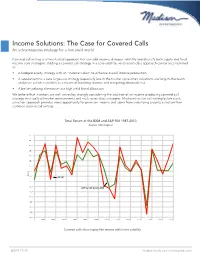
  • Income Solutions: the Case for Covered Calls an Advantageous Strategy for a Low-Yield World
    Income Solutions: The Case for Covered Calls An advantageous strategy for a low-yield world Covered call writing is a time-tested approach that can add income, dampen volatility and diversify both equity and fixed income core strategies. Adding a covered call strategy in a core-satellite, multi-asset-class approach can be accomplished as: • A hedged equity strategy with an “income kicker” to enhance overall income production • A supplement to a core large-cap strategy (especially late in the market cycle when valuations are long-in-the-tooth and price action is volatile) as a means of boosting income and mitigating downside risk • A better-yielding alternative to a high yield bond allocation We believe that investors are well-served by strongly considering the addition of an income-producing covered call strategy in virtually all market environments and multi-asset class strategies. Madison’s active call writing/active stock selection approach provides more opportunity for premium income and alpha from underlying security selection than common passive call writing. Total Return of the BXM and S&P 500 1987-2013 Rolling Returns Source: Morningstar Time Period: 1/1/1987 to 12/31/2013 Rolling Window: 1 Year 1 Year shift 40.0 35.0 30.0 25.0 20.0 15.0 10.0 5.0 Return 0.0 S&P 500 -5.0 -10.0 CBOE S&P 500 Buywrite BXM -15.0 -20.0 -25.0 -30.0 -35.0 -40.0 1989 1991 1993 1995 1997 1999 2001 2003 2005 2007 2009 2011 2013 S&P 500 TR USD Covered calls show equity-likeCBOE returns S&P 500 with Buyw ritelower BXM volatility Source: Morningstar Direct 888.971.7135 madisonfunds.com | madisonadv.com Covered Call Strategy(A) Benefits of Individual Stock Options vs.
    [Show full text]
  • Structured Products in Asia
    2015 ISSUE: NOVEMBER Structured Products in Asia hubbis.com 1st Leonteq has received more than 20 awards since its foundation in 2007 THE QUINTESSENCE OF OUR MISSION STATEMENT LET´S REDEFINE YOUR INVESTMENT EXPERIENCE Leonteq’s explicit goal is to make a difference through particular transparency in structured investment products and to be the preferred technology and service partner for investment solutions. We count on experienced industry experts with a focus on achieving client’s goals and a fi rst class IT infrastructure, setting new stand- ards in stability and fl exibility. OUR DIFFERENTIATION Modern platform • Integrated IT platform built from ground up with a focus on automation of key processes in the value chain • Platform functionality to address increased customer demand for transparency, service, liquidity, security and sustainability Vertical integration • Control of the entire value chain as a basis for proactive service tailored to specifi c needs of clients • Automation of key processes mitigating operational risks Competitive cost per issued product • Modern platform resulting in a competitive cost per issued product allowing for small ticket sizes LEGAL DISCLAIMER Leonteq Securities (Hong Kong) Limited (CE no.AVV960) (“Leonteq Hong Kong”) is responsible for the distribution of this publication in Hong Kong. It is licensed and regulated by the Hong Kong Securities and Futures Commission for Types 1 and 4 regulated activities. The services and products it provides are available only to “profes- sional investors” as defi ned in the Securities and Futures Ordinance (Cap. 571) of Hong Kong. This document is being communicated to you solely for the purposes of providing information regarding the products and services that the Leonteq group currently offers, subject to applicable laws and regulations.
    [Show full text]
  • Options Strategy Guide for Metals Products As the World’S Largest and Most Diverse Derivatives Marketplace, CME Group Is Where the World Comes to Manage Risk
    metals products Options Strategy Guide for Metals Products As the world’s largest and most diverse derivatives marketplace, CME Group is where the world comes to manage risk. CME Group exchanges – CME, CBOT, NYMEX and COMEX – offer the widest range of global benchmark products across all major asset classes, including futures and options based on interest rates, equity indexes, foreign exchange, energy, agricultural commodities, metals, weather and real estate. CME Group brings buyers and sellers together through its CME Globex electronic trading platform and its trading facilities in New York and Chicago. CME Group also operates CME Clearing, one of the largest central counterparty clearing services in the world, which provides clearing and settlement services for exchange-traded contracts, as well as for over-the-counter derivatives transactions through CME ClearPort. These products and services ensure that businesses everywhere can substantially mitigate counterparty credit risk in both listed and over-the-counter derivatives markets. Options Strategy Guide for Metals Products The Metals Risk Management Marketplace Because metals markets are highly responsive to overarching global economic The hypothetical trades that follow look at market position, market objective, and geopolitical influences, they present a unique risk management tool profit/loss potential, deltas and other information associated with the 12 for commercial and institutional firms as well as a unique, exciting and strategies. The trading examples use our Gold, Silver
    [Show full text]
  • Bankruptcy Futures: Hedging Against Credit Card Default
    CONSUMER LENDING Bankruptcy Futures: Hedging Against Credit Card Default by Russ Ray his article discusses the new bankruptcy futures contract to be launched by the Chicago Mercantile Exchange and examines the mechanics and contract specifications of this innovation, illus- trating its hedging potential in the process. ometime during the latter half of 1999 or early Credit-card debt is becoming particularly burden- 2000, the Chicago Mercantile Exchange intends some. The average credit-card balance is approximately to launch an innovative new futures contract that $2,500, with typical households having at least three dif- will offer consumer-lending institutions, particularly ferent bank cards. The average card holder also uses six credit-card issuers, a hedge against the bankruptcies additional cards at service stations, department stores, filed by their borrowers. Bankruptcy futures—contracts specialty stores, and other vendors issuing their own cred- to buy or sell a cash-valued index based upon the cur- it cards. rent number of actual bankruptcies—will enable con- Commensurate with such increases in consumer sumer lenders to transfer default risk to other lenders debt is an ever-growing rise in consumer bankruptcies, and/or speculators holding opposite expectations. which, in turn, represent an ever-increasing proportion Significantly, this new contract also constitutes a proxy of total bankruptcies. In 1998, 96.9% of all bankruptcy variable for banks' confidence in the value and liquidity filings were personal—not business—bankruptcies. (In of their own loan portfolios, just as other proxy vari- terms of dollar volume, however, businesses continue to ables now measure consumer and investor confidence.
    [Show full text]
  • Derivative Securities
    2. DERIVATIVE SECURITIES Objectives: After reading this chapter, you will 1. Understand the reason for trading options. 2. Know the basic terminology of options. 2.1 Derivative Securities A derivative security is a financial instrument whose value depends upon the value of another asset. The main types of derivatives are futures, forwards, options, and swaps. An example of a derivative security is a convertible bond. Such a bond, at the discretion of the bondholder, may be converted into a fixed number of shares of the stock of the issuing corporation. The value of a convertible bond depends upon the value of the underlying stock, and thus, it is a derivative security. An investor would like to buy such a bond because he can make money if the stock market rises. The stock price, and hence the bond value, will rise. If the stock market falls, he can still make money by earning interest on the convertible bond. Another derivative security is a forward contract. Suppose you have decided to buy an ounce of gold for investment purposes. The price of gold for immediate delivery is, say, $345 an ounce. You would like to hold this gold for a year and then sell it at the prevailing rates. One possibility is to pay $345 to a seller and get immediate physical possession of the gold, hold it for a year, and then sell it. If the price of gold a year from now is $370 an ounce, you have clearly made a profit of $25. That is not the only way to invest in gold.
    [Show full text]
  • Form 6781 Contracts and Straddles ▶ Go to for the Latest Information
    Gains and Losses From Section 1256 OMB No. 1545-0644 Form 6781 Contracts and Straddles ▶ Go to www.irs.gov/Form6781 for the latest information. 2020 Department of the Treasury Attachment Internal Revenue Service ▶ Attach to your tax return. Sequence No. 82 Name(s) shown on tax return Identifying number Check all applicable boxes. A Mixed straddle election C Mixed straddle account election See instructions. B Straddle-by-straddle identification election D Net section 1256 contracts loss election Part I Section 1256 Contracts Marked to Market (a) Identification of account (b) (Loss) (c) Gain 1 2 Add the amounts on line 1 in columns (b) and (c) . 2 ( ) 3 Net gain or (loss). Combine line 2, columns (b) and (c) . 3 4 Form 1099-B adjustments. See instructions and attach statement . 4 5 Combine lines 3 and 4 . 5 Note: If line 5 shows a net gain, skip line 6 and enter the gain on line 7. Partnerships and S corporations, see instructions. 6 If you have a net section 1256 contracts loss and checked box D above, enter the amount of loss to be carried back. Enter the loss as a positive number. If you didn’t check box D, enter -0- . 6 7 Combine lines 5 and 6 . 7 8 Short-term capital gain or (loss). Multiply line 7 by 40% (0.40). Enter here and include on line 4 of Schedule D or on Form 8949. See instructions . 8 9 Long-term capital gain or (loss). Multiply line 7 by 60% (0.60). Enter here and include on line 11 of Schedule D or on Form 8949.
    [Show full text]
  • Futures Options: Universe of Potential Profit
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Directory of Open Access Journals Annals of the „Constantin Brâncuşi” University of Târgu Jiu, Economy Series, Issue 2/2013 FUTURES OPTIONS: UNIVERSE OF POTENTIAL PROFIT Teselios Delia PhD Lecturer, “Constantin Brancoveanu” University of Pitesti, Romania [email protected] Abstract A approaching options on futures contracts in the present paper is argued, on one hand, by the great number of their directions for use (in financial speculation, in managing and risk control, etc.) and, on the other hand, by the fact that in Romania, nowadays, futures contracts and options represent the main categories of traded financial instruments. Because futures contract, as an underlying asset for options, it is often more liquid and involves more reduced transaction costs than cash product which corresponds to that futures contract, this paper presents a number of information regarding options on futures contracts, which offer a wide range of investment opportunities, being used to protect against adverse price moves in commodity, interest rate, foreign exchange and equity markets. There are presented two assessment models of these contracts, namely: an expansion of the Black_Scholes model published in 1976 by Fischer Black and the binomial model used especially for its flexibility. Likewise, there are presented a series of operations that can be performed using futures options and also arguments in favor of using these types of options. Key words: futures options, futures contracts, binomial model, straddle, strangle JEL Classification: G10, G13, C02. Introduction Economies and investments play a particularly important role both at macroeconomic level and at the level of each person or company.
    [Show full text]
  • Financial Derivatives Classification of Derivatives
    FINANCIAL DERIVATIVES A derivative is a financial instrument or contract that derives its value from an underlying asset. The buyer agrees to purchase the asset on a specific date at a specific price. Derivatives are often used for commodities, such as oil, gasoline, or gold. Another asset class is currencies, often the U.S. dollar. There are derivatives based on stocks or bonds. The most common underlying assets include stocks, bonds, commodities, currencies, interest rates and market indexes. The contract's seller doesn't have to own the underlying asset. He can fulfill the contract by giving the buyer enough money to buy the asset at the prevailing price. He can also give the buyer another derivative contract that offsets the value of the first. This makes derivatives much easier to trade than the asset itself. According to the Securities Contract Regulation Act, 1956 the term ‘Derivative’ includes: i. a security derived from a debt instrument, share, loan, whether secured or unsecured, risk instrument or contract for differences or any other form of security. ii. a contract which derives its value from the prices or index of prices, of underlying securities. CLASSIFICATION OF DERIVATIVES Derivatives can be classified into broad categories depending upon the type of underlying asset, the nature of derivative contract or the trading of derivative contract. 1. Commodity derivative and Financial derivative In commodity derivatives, the underlying asset is a commodity, such as cotton, gold, copper, wheat, or spices. Commodity derivatives were originally designed to protect farmers from the risk of under- or overproduction of crops. Commodity derivatives are investment tools that allow investors to profit from certain commodities without possessing them.
    [Show full text]
  • EQUITY DERIVATIVES Faqs
    NATIONAL INSTITUTE OF SECURITIES MARKETS SCHOOL FOR SECURITIES EDUCATION EQUITY DERIVATIVES Frequently Asked Questions (FAQs) Authors: NISM PGDM 2019-21 Batch Students: Abhilash Rathod Akash Sherry Akhilesh Krishnan Devansh Sharma Jyotsna Gupta Malaya Mohapatra Prahlad Arora Rajesh Gouda Rujuta Tamhankar Shreya Iyer Shubham Gurtu Vansh Agarwal Faculty Guide: Ritesh Nandwani, Program Director, PGDM, NISM Table of Contents Sr. Question Topic Page No No. Numbers 1 Introduction to Derivatives 1-16 2 2 Understanding Futures & Forwards 17-42 9 3 Understanding Options 43-66 20 4 Option Properties 66-90 29 5 Options Pricing & Valuation 91-95 39 6 Derivatives Applications 96-125 44 7 Options Trading Strategies 126-271 53 8 Risks involved in Derivatives trading 272-282 86 Trading, Margin requirements & 9 283-329 90 Position Limits in India 10 Clearing & Settlement in India 330-345 105 Annexures : Key Statistics & Trends - 113 1 | P a g e I. INTRODUCTION TO DERIVATIVES 1. What are Derivatives? Ans. A Derivative is a financial instrument whose value is derived from the value of an underlying asset. The underlying asset can be equity shares or index, precious metals, commodities, currencies, interest rates etc. A derivative instrument does not have any independent value. Its value is always dependent on the underlying assets. Derivatives can be used either to minimize risk (hedging) or assume risk with the expectation of some positive pay-off or reward (speculation). 2. What are some common types of Derivatives? Ans. The following are some common types of derivatives: a) Forwards b) Futures c) Options d) Swaps 3. What is Forward? A forward is a contractual agreement between two parties to buy/sell an underlying asset at a future date for a particular price that is pre‐decided on the date of contract.
    [Show full text]
  • Covered Calls Uncovered Roni Israelov and Lars N
    Financial Analysts Journal Volume 71 · Number 6 ©2015 CFA Institute Covered Calls Uncovered Roni Israelov and Lars N. Nielsen Typical covered call strategies collect the equity and volatility risk premiums but also embed exposure to a naive equity reversal strategy that is uncompensated. This article presents a novel risk and performance attribu- tion methodology that deconstructs the strategy into these three exposures. Historically, the equity exposure contributed most of the risk and return. The short volatility exposure realized a Sharpe ratio of nearly 1.0 but contributed only 10% of the risk. The equity reversal exposure contributed approximately 25% of the risk but provided little return in exchange. The authors propose a risk-managed covered call strategy that eliminates the uncompensated equity reversal exposure. This modified covered call strategy has a superior Sharpe ratio, reduced volatility, and reduced downside equity beta. quity index covered calls are the most easily by natural buyers can lead to a risk premium. accessible source of the volatility risk pre- Litterman (2011) suggested that long-term inves- Emium for most investors.1 The volatility risk tors, such as pensions and endowments, should be premium, which is absent from most investors’ port- natural providers of financial insurance and sellers folios, has had more than double the risk-adjusted of options. returns (Sharpe ratio) of the equity risk premium, Yet, many investors remain skeptical of covered which is the dominant source of return for most call strategies. Although deceptively simple—long investors. By providing the equity and volatility equity and short a call option—covered calls are not risk premiums, equity index covered calls’ returns well understood.
    [Show full text]