Lagrangian Coherent Structures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Title: Fractals Topics: Symmetry, Patterns in Nature, Biomimicry Related Disciplines: Mathematics, Biology Objectives: A. Learn
Title: Fractals Topics: symmetry, patterns in nature, biomimicry Related Disciplines: mathematics, biology Objectives: A. Learn about how fractals are made. B. Think about the mathematical processes that play out in nature. C. Create a hands-on art project. Lesson: A. Introduction (20 minutes) Fractals are sets in mathematics based on repeated processes at different scales. Why do we care? Fractals are a part of nature, geometry, algebra, and science and are beautiful in their complexity. Fractals come in many types: branching, spiral, algebraic, and geometric. Branching and spiral fractals can be found in nature in many different forms. Branching is seen in trees, lungs, snowflakes, lightning, and rivers. Spirals are visible in natural forms such as hurricanes, shells, liquid motion, galaxies, and most easily visible in plants like flowers, cacti, and Romanesco Figure 1: Romanesco (Figure 1). Branching fractals emerge in a linear fashion. Spirals begin at a point and expand out in a circular motion. A cool demonstration of branching fractals can be found at: http://fractalfoundation.org/resources/what-are-fractals/. Algebraic fractals are based on surprisingly simple equations. Most famous of these equations is the Mandelbrot Set (Figure 2), a plot made from the equation: The most famous of the geometric fractals is the Sierpinski Triangle: As seen in the diagram above, this complex fractal is created by starting with a single triangle, then forming another inside one quarter the size, then three more, each one quarter the size, then 9, 27, 81, all just one quarter the size of the triangle drawn in the previous step. -

Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected]
University of Massachusetts Amherst ScholarWorks@UMass Amherst Patterns Around Us STEM Education Institute 2017 Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected] Wayne Kermenski Hawlemont Regional School, [email protected] Follow this and additional works at: https://scholarworks.umass.edu/stem_patterns Part of the Biology Commons, Physics Commons, Science and Mathematics Education Commons, and the Teacher Education and Professional Development Commons Welborn, Jennifer and Kermenski, Wayne, "Branching in Nature" (2017). Patterns Around Us. 2. Retrieved from https://scholarworks.umass.edu/stem_patterns/2 This Article is brought to you for free and open access by the STEM Education Institute at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Patterns Around Us by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. Patterns Around Us: Branching in Nature Teacher Resource Page Part A: Introduction to Branching Massachusetts Frameworks Alignment—The Nature of Science • Overall, the key criterion of science is that it provide a clear, rational, and succinct account of a pattern in nature. This account must be based on data gathering and analysis and other evidence obtained through direct observations or experiments, reflect inferences that are broadly shared and communicated, and be accompanied by a model that offers a naturalistic explanation expressed in conceptual, mathematical, and/or mechanical terms. Materials: -

Art on a Cellular Level Art and Science Educational Resource
Art on a Cellular Level Art and Science Educational Resource Phoenix Airport Museum Educators and Parents, With foundations in art, geometry and plant biology, the objective of this lesson is to recognize patterns and make connections between the inexhaustible variety of life on our planet. This educational resource is geared for interaction with students of all ages to support the understanding between art and science. It has been designed based on our current exhibition, Art on a Cellular Level, on display at Sky Harbor. The questions and activities below were created to promote observation and curiosity. There are no wrong answers. You may print this PDF to use as a workbook or have your student refer to the material online. We encourage educators to expand on this art and science course to create a lesson plan. If you enjoy these activities and would like to investigate further, check back for new projects each week (three projects total). We hope your student will have fun with this and make an art project to share with us. Please send an image of your student’s artwork to [email protected] or hashtag #SkyHarborArts for an opportunity to be featured on Phoenix Sky Harbor International Airport’s social media. Art on a Cellular Level exhibition Sky Harbor, Terminal 4, level 3 Gallery Art is a lens through which we view the world. It can be a tool for storytelling, expressing cultural values and teaching fundamentals of math, technology and science in a visual way. The Terminal 4 gallery exhibition, Art on a Cellular Level, examines the intersections between art and science. -
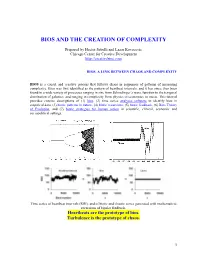
Bios and the Creation of Complexity
BIOS AND THE CREATION OF COMPLEXITY Prepared by Hector Sabelli and Lazar Kovacevic Chicago Center for Creative Development http://creativebios.com BIOS, A LINK BETWEEN CHAOS AND COMPLEXITY BIOS is a causal and creative process that follows chaos in sequences of patterns of increasing complexity. Bios was first identified as the pattern of heartbeat intervals, and it has since then been found in a wide variety of processes ranging in size from Schrodinger’s wave function to the temporal distribution of galaxies, and ranging in complexity from physics to economics to music. This tutorial provides concise descriptions of (1) bios, (2) time series analyses software to identify bios in empirical data, (3) biotic patterns in nature, (4) biotic recursions, (5) biotic feedback, (6) Bios Theory of Evolution, and (7) biotic strategies for human action in scientific, clinical, economic and sociopolitical settings. Time series of heartbeat intervals (RRI), and of biotic and chaotic series generated with mathematical recursions of bipolar feedback. Heartbeats are the prototype of bios. Turbulence is the prototype of chaos. 1 1. BIOS BIOS is an expansive process with chaotic features generated by feedback and characterized by features of creativity. Process: Biotic patterns are sequences of actions or states. Expansive: Biotic patterns continually expand in their diversity and often in their range. This is significant, as natural processes expand, in contrast to convergence to equilibrium, periodic, or chaotic attractors. Expanding processes range from the universe to viruses, and include human populations, empires, ideas and cultures. Chaotic: Biotic series are aperiodic and generated causally; mathematically generated bios is extremely sensitive to initial conditions. -

Pattern Formation in Nature: Physical Constraints and Self-Organising Characteristics
Pattern formation in nature: Physical constraints and self-organising characteristics Philip Ball ________________________________________________________________ Abstract The formation of patterns is apparent in natural systems ranging from clouds to animal markings, and from sand dunes to the intricate shells of microscopic marine organisms. Despite the astonishing range and variety of such structures, many seem to have analogous features: the zebra’s stripes put us in mind of the ripples of blown sand, for example. In this article I review some of the common patterns found in nature and explain how they are typically formed through simple, local interactions between many components of a system – a form of physical computation that gives rise to self- organisation and emergent structures and behaviours. ________________________________________________________________ Introduction When the naturalist Joseph Banks first encountered Fingal’s Cave on the Scottish island of Staffa, he was astonished by the quasi-geometric, prismatic pillars of rock that flank the entrance. As Banks put it, Compared to this what are the cathedrals or palaces built by men! Mere models or playthings, as diminutive as his works will always be when compared with those of nature. What now is the boast of the architect! Regularity, the only part in which he fancied himself to exceed his mistress, Nature, is here found in her possession, and here it has been for ages undescribed. This structure has a counterpart on the coast of Ireland: the Giant’s Causeway in County Antrim, where again one can see the extraordinarily regular and geometric honeycomb structure of the fractured igneous rock (Figure 1). When we make an architectural pattern like this, it is through careful planning and construction, with each individual element cut to shape and laid in place. -

Fractal Art: Closer to Heaven? Modern Mathematics, the Art of Nature, and the Nature of Art
Fractal Art: Closer to Heaven? Modern Mathematics, the art of Nature, and the nature of Art Charalampos Saitis Music & Media Technologies Dept. of Electronic & Electrical Engineering University of Dublin, Trinity College Printing House, Trinity College Dublin 2, Ireland [email protected] Abstract Understanding nature has always been a reference point for both art and science. Aesthetics have put nature at the forefront of artistic achievement. Artworks are expected to represent nature, to work like it. Science has likewise been trying to explain the very laws that determine nature. Technology has provided both sides with the appropriate tools towards their common goal. Fractal art stands right at the heart of the art-science-technology triangle. This paper examines the new perspectives brought to art by fractal geometry and chaos theory and how the study of the fractal character of nature offers promising possibilities towards art’s mission. Introduction “When I judge art, I take my painting and put it next to a God-made object like a tree or flower. If it clashes, it is not art.” Paul Cézanne [1] Mathematics has always been affecting art. Mathematical concepts such as the golden ratio, the platonic solids and the projective geometry have been widely used by painters and sculptors whereas the Pythagorean arithmetic perception of harmony dominates western music to this very day. Infinity and probability theory inspired artists such as M. C. Escher and composers such as Iannis Xenakis forming trends in contemporary art and music. The evolution of technology created new areas of intersection between mathematics and art or music: digital art, computer music and new media. -

Regulation of Phyllotaxis
CORE Metadata, citation and similar papers at core.ac.uk Published in "International Journal of Developmental Biology 49: 539-546, 2005" Provided by RERO DOC Digital Library which should be cited to refer to this work. Regulation of phyllotaxis DIDIER REINHARDT* Plant Biology, Department of Biology, Fribourg, Switzerland ABSTRACT Plant architecture is characterized by a high degree of regularity. Leaves, flowers and floral organs are arranged in regular patterns, a phenomenon referred to as phyllotaxis. Regular phyllotaxis is found in virtually all higher plants, from mosses, over ferns, to gymnosperms and angiosperms. Due to its remarkable precision, its beauty and its accessibility, phyllotaxis has for centuries been the object of admiration and scientific examination. There have been numerous hypotheses to explain the nature of the mechanistic principle behind phyllotaxis, however, not all of them have been amenable to experimental examination. This is due mainly to the delicacy and small size of the shoot apical meristem, where plant organs are formed and the phyllotactic patterns are laid down. Recently, the combination of genetics, molecular tools and micromanipulation has resulted in the identification of auxin as a central player in organ formation and positioning. This paper discusses some aspects of phyllotactic patterns found in nature and summarizes our current understanding of the regulatory mechanism behind phyllotaxis. KEY WORDS: phyllotaxis, meristem, auxin, Arabidopsis, tomato Introduction formed simultaneously. Spiral phyllotaxis is the most common pattern and is found in model plant species such as Arabidopsis, The architecture of plants is highly regular. For example, flowers tobacco and tomato. An important model system for the study of exhibit characteristic symmetric arrangement of their organs; the distichous phyllotaxis is maize. -
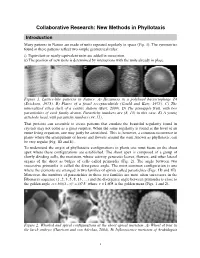
Collaborative Research: New Methods in Phyllotaxis
Collaborative Research: New Methods in Phyllotaxis Introduction Many patterns in Nature are made of units repeated regularly in space (Fig. 1). The symmetries found in these patterns reflect two simple geometrical rules: i) Equivalent or nearly equivalent units are added in succession. ii) The position of new units is determined by interactions with the units already in place. Figure 1. Lattice-like patterns in Nature. A) Hexamers in a polyhead bacteriophage T4 (Erickson, 1973). B) Plates of a fossil receptaculitids (Gould and Katz, 1975). C) The mineralized silica shell of a centric diatom (Bart, 2000). D) The pineapple fruit, with two parastichies of each family drawn. Parastichy numbers are (8, 13) in this case. E) A young artichoke head, with parastichy numbers (34, 55). That proteins can assemble to create patterns that emulate the beautiful regularity found in crystals may not come as a great surprise. When the same regularity is found at the level of an entire living organism, one may justly be astonished. This is, however, a common occurrence in plants where the arrangement of leaves and flowers around the stem, known as phyllotaxis, can be very regular (Fig. 1D and E). To understand the origin of phyllotactic configurations in plants one must focus on the shoot apex where these configurations are established. The shoot apex is composed of a group of slowly dividing cells, the meristem, whose activity generates leaves, flowers, and other lateral organs of the shoot as bulges of cells called primordia (Fig. 2). The angle between two successive primordia is called the divergence angle. -

On Growth and Form
On Growth and Form On Growth and Form On Growth and Form This collection of essays by architects and artists revisits D’Arcy Thompson’s influential bookOn Growth and Form Organic Architecture and Beyond (1917) to explore the link between morphology and form- making in historical and contemporary design. This book sheds new light on architects’ ongoing fascination with Edited by Philip Beesley & Sarah Bonnemaison organicism, and the relation between nature and artifice that makes our world. Beesley • Bonnemaison on growth and form Organic architecture and beyond Tuns Press and Riverside Architectural Press 2 on growth and form Tuns Press Faculty of Architecture and Planning Dalhousie University P.O. Box 1000, Halifax, NS Canada B3J 2X4 web: tunspress.dal.ca © 2008 by Tuns Press and Riverside Architectural Press All Rights Reserved. Published March 2008 Printed in Canada Library and Archives Canada Cataloguing in Publication On growth and form : organic architecture and beyond / edited by Sarah Bonnemaison and Philip Beesley. Includes bibliographical references. ISBN 978-0-929112-54-1 1. Organic architecture. 2. Nature (Aesthetics) 3. Thompson, D’Arcy Wentworth, 1860-1948. On growth and form. I. Bonnemaison, Sarah, 1958- II. Beesley, Philip, 1956- NA682.O73O6 2008 720’.47 C2008-900017-X contents 7 Why Revisit D’Arcy Wentworth Thompson’sOn Growth and Form? Sarah Bonnemaison and Philip Beesley history and criticism 16 Geometries of Creation: Architecture and the Revision of Nature Ryszard Sliwka 30 Old and New Organicism in Architecture: The Metamorphoses of an Aesthetic Idea Dörte Kuhlmann 44 Functional versus Purposive in the Organic Forms of Louis Sullivan and Frank Lloyd Wright Kevin Nute 54 The Forces of Matter Hadas A. -

Inhibition Fields for Phyllotactic Pattern Formation: a Simulation Study1
1635 Inhibition fields for phyllotactic pattern formation: a simulation study1 Richard S. Smith, Cris Kuhlemeier, and Przemyslaw Prusinkiewicz Abstract: Most theories of phyllotaxis are based on the idea that the formation of new primordia is inhibited by the prox- imity of older primordia. Several mechanisms that could result in such an inhibition have been proposed, including me- chanical interactions, diffusion of a chemical inhibitor, and signaling by actively transported substances. Despite the apparent diversity of these mechanisms, their pattern-generation properties can be captured in a unified manner by inhibi- tion fields surrounding the existing primordia. In this paper, we introduce a class of fields that depend on both the spatial distribution and the age of previously formed primordia. Using current techniques to create geometrically realistic, growing apex surfaces, we show that such fields can robustly generate a wide range of spiral, multijugate, and whorled phyllotactic patterns and their transitions. The mathematical form of the inhibition fields suggests research directions for future studies of phyllotactic patterning mechanisms. Key words: morphogenesis, spiral, whorl, inhibition, modeling, visualization. Re´sume´ : La plupart des the´ories phyllotaxiques sont base´es sur l’ide´e que la formation de nouveaux primordiums est in- hibe´e par la proximite´ de prirmordiums plus aˆge´s. On a propose´ plusieurs me´canismes qui pourraient conduire a` une telle inhibition, incluant des interactions me´caniques, la diffusion d’un inhibiteur chimique, et une signalisation par des substan- ces activement transporte´es. En de´pit de la diversite´ de ces me´canismes, les proprie´te´s de leur patron de de´veloppement peuvent eˆtre perc¸ues de manie`re unifie´e, par des champs d’inhibition autour des primordiums existants. -

Adaptive Inference for Distinguishing Credible from Incredible Patterns in Nature
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Nebraska Cooperative Fish & Wildlife Research Nebraska Cooperative Fish & Wildlife Research Unit -- Staff Publications Unit 2002 Adaptive Inference for Distinguishing Credible from Incredible Patterns in Nature C. S. Holling University of Florida Craig R. Allen University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/ncfwrustaff Part of the Other Environmental Sciences Commons Holling, C. S. and Allen, Craig R., "Adaptive Inference for Distinguishing Credible from Incredible Patterns in Nature" (2002). Nebraska Cooperative Fish & Wildlife Research Unit -- Staff Publications. 1. https://digitalcommons.unl.edu/ncfwrustaff/1 This Article is brought to you for free and open access by the Nebraska Cooperative Fish & Wildlife Research Unit at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Nebraska Cooperative Fish & Wildlife Research Unit -- Staff Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Ecosystems (2002) 5: 319–328 DOI: 10.1007/s10021-001-0076-2 ECOSYSTEMS © 2002 Springer-Verlag Adaptive Inference for Distinguishing Credible from Incredible Patterns in Nature C. S. Holling1 and Craig R. Allen2* 1Department of Zoology, 110 Bartram, University of Florida, Gainesville, Florida 32611, USA; and 2US Geological Survey, Biological Resources Division, South Carolina Cooperative Fish and Wildlife Research Unit, Clemson -

Working with Fractals a Resource for Practitioners of Biophilic Design
WORKING WITH FRACTALS A RESOURCE FOR PRACTITIONERS OF BIOPHILIC DESIGN A PROJECT OF THE EUROPEAN ‘COST RESTORE ACTION’ PREPARED BY RITA TROMBIN IN COLLABORATION WITH ACKNOWLEDGEMENTS This toolkit is the result of a joint effort between Terrapin Bright Green, Cost RESTORE Action (REthinking Sustainability TOwards a Regenerative Economy), EURAC Research, International Living Future Institute, Living Future Europe and many other partners, including industry professionals and academics. AUTHOR Rita Trombin SUPERVISOR & EDITOR Catherine O. Ryan CONTRIBUTORS Belal Abboushi, Pacific Northwest National Laboratory (PNNL) Luca Baraldo, COOKFOX Architects DCP Bethany Borel, COOKFOX Architects DCP Bill Browning, Terrapin Bright Green Judith Heerwagen, University of Washington Giammarco Nalin, Goethe Universität Kari Pei, Interface Nikos Salingaros, University of Texas at San Antonio Catherine Stolarski, Catherine Stolarski Design Richard Taylor, University of Oregon Dakota Walker, Terrapin Bright Green Emily Winer, International Well Building Institute CITATION Rita Trombin, ‘Working with fractals: a resource for practitioners of biophilic design’. Report, Terrapin Bright Green: New York, 31 December 2020. Revised January 2021 © 2020 Terrapin Bright Green LLC For inquiries: [email protected] or [email protected] COVER DESIGN: Catherine O. Ryan COVER IMAGES: Ice crystals (snow-603675) by Quartzla from Pixabay; fractal gasket snowflake by Catherine Stolarski Design. 2 Working with Fractals: A Toolkit © 2020 Terrapin Bright Green LLC OVERVIEW The unique trademark of nature to make complexity comprehensible is underpinned by fractal patterns – self-similar patterns over a range of magnification scales – that apply to virtually any domain of life. For the design of built environment, fractal patterns may present opportunities to positively impact human perception, health, cognitive performance, emotions and stress.