DOCSLIB.ORG

Working with Fractals a Resource for Practitioners of Biophilic Design

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Working with Fractals a Resource for Practitioners of Biophilic Design WORKING WITH FRACTALS A RESOURCE FOR PRACTITIONERS OF BIOPHILIC DESIGN A PROJECT OF THE EUROPEAN ‘COST RESTORE ACTION’ PREPARED BY RITA TROMBIN IN COLLABORATION WITH ACKNOWLEDGEMENTS This toolkit is the result of a joint effort between Terrapin Bright Green, Cost RESTORE Action (REthinking Sustainability TOwards a Regenerative Economy), EURAC Research, International Living Future Institute, Living Future Europe and many other partners, including industry professionals and academics. AUTHOR Rita Trombin SUPERVISOR & EDITOR Catherine O. Ryan CONTRIBUTORS Belal Abboushi, Pacific Northwest National Laboratory (PNNL) Luca Baraldo, COOKFOX Architects DCP Bethany Borel, COOKFOX Architects DCP Bill Browning, Terrapin Bright Green Judith Heerwagen, University of Washington Giammarco Nalin, Goethe Universität Kari Pei, Interface Nikos Salingaros, University of Texas at San Antonio Catherine Stolarski, Catherine Stolarski Design Richard Taylor, University of Oregon Dakota Walker, Terrapin Bright Green Emily Winer, International Well Building Institute CITATION Rita Trombin, ‘Working with fractals: a resource for practitioners of biophilic design’. Report, Terrapin Bright Green: New York, 31 December 2020. Revised January 2021 © 2020 Terrapin Bright Green LLC For inquiries: [email protected] or [email protected] COVER DESIGN: Catherine O. Ryan COVER IMAGES: Ice crystals (snow-603675) by Quartzla from Pixabay; fractal gasket snowflake by Catherine Stolarski Design. 2 Working with Fractals: A Toolkit © 2020 Terrapin Bright Green LLC OVERVIEW The unique trademark of nature to make complexity comprehensible is underpinned by fractal patterns – self-similar patterns over a range of magnification scales – that apply to virtually any domain of life. For the design of built environment, fractal patterns may present opportunities to positively impact human perception, health, cognitive performance, emotions and stress. Yet, designing with fractals can also come with implementation challenges. In 2014, Terrapin Bright Green classified fractals under the biophilic design pattern ‘Complexity and Order’, as to indicate “rich sensory information that adheres to a spatial hierarchy similar to those encountered in nature”. Today we recognize that fractals, can span beyond a single pattern to help characterize form, light, sound, and even spatial characteristics. With the recent surge of interest in fractal geometries – both among peer-reviewed research outputs and as a particularly accessible design attribute for architects and interior designers – Terrapin identified the need for a design-oriented document addressing key learning points for design practitioners interested in working with fractals. Significant research insights can take an average of 17 years before making it into industry practice. As a joint effort between Terrapin, Cost RESTORE Action, Eurac Research, International Living Future Institute, this project aims help shorten that gap. By identifying the most appropriate data and resources, this work hopes to advance the understanding and discussion of fractals for direct application by the design community and related sectors and industries. This paper focuses on the research and design opportunities supporting the visual experience of fractals for the indoor environment. The aim of this paper (PART 1) and toolkit (PART 2) is to: • Appreciate the value of fractal patterns and incorporate them within their projects. • Illustrate that nature-based fractal patterns can lead to significant positive health benefits. • Encourage product and material selection featuring fractal patterns to optimise associated health benefits. PART 1: FOR THE LOVE OF FRACTALS THE HISTORY AND SCIENCE OF FRACTALS FOR INDOOR ENVIRONMENTAL HEALTH PART 2: WORKING WITH FRACTALS A TOOLKIT FOR DESIGNERS 3 Working with Fractals: A Toolkit © 2020 Terrapin Bright Green LLC PART 1 FOR THE LOVE OF FRACTALS THE HISTORY AND SCIENCE OF FRACTALS FOR INDOOR ENVIRONMENTAL HEALTH FRACTAL FLUENCY, A TRADEMARK OF NATURE FRACTAL DESIGN, ARCHITECTURE AND ART What is perhaps most intriguing is that the appeal IN HUMAN HISTORY of fractals is potentially innate and not learned, as adult-like preferences for fractals have been detected Fractals have permeated cultures spanning across in urban-raised children as young as three years old many centuries and continents, classical art and (Robles et al., 2020). vernacular architecture from the column capitals of ancient Greece, Egyptian, Aztec, Incan civilisations, the art of Ancient Mayans, Islamic and Hindu temples, FRACTALS AS NATURAL PHENOMENA Angkor Wat in Cambodia, the Eiffel Tower in Paris, and Nature is characterized by a particular type of statistical the structures of Santiago Calatrava. Fractals are also geometry, different from Euclidean geometry, called evident in such well known works as those of Botticelli, fractal geometry (Mandelbrot, 1982). Humans evolved in Vincent van Gogh, and Jackson Pollock. Their visual complex and sensory rich natural environments, where all properties were also explored by mathematicians of natural structure are fractals on a hierarchy of scales, when Benoit Mandelbrot published The Fractal from the large to the microscopic. At present, the majority Geometry of Nature (1982) in which he catalogued of global population live in built urban environments nature’s statistical fractals and discussed them using characterised by minimalist/Euclidian architecture (e.g., mathematical methods for their replication. straight lines, right angles, empty planes, rectangles, Fractals constitute a central component of human cubes, cylinders, etc.) resulting in spaces that do not daily experience of the environment (Taylor & Spehar, adequately nurture and revitalise. Abundant research in 2016). While extensive research has documented the environmental psychology suggests that humans need negative effects of environments that do not have fractal scales, rich patterning, spatial layering, and a complement of rich experiential aesthetic variety interlocking geometries that are typical of nature. From (Mehaffy & Salingaros, 2013), their proliferation in an evolutionary standpoint we could venture to surmise art and design has continued to grow and diversify, that humans are instinctively drawn to fractal features creating architecture, interiors and products designed for their survival value. Within a contemporary context, a for human needs (Taylor & Spehar, 2016). Over good habitat is one in which people can function at their the past two decades, interdisciplinary teams have optimal potential (Kellert & Calabrese, 2015); thus, when confirmed that the aesthetic qualities of nature’s nature’s trademark for complexity and order is applied fractal patterns can induce striking effects on health.1 to architecture and design, restorative, nourishing and satisfying spaces, products and materials result. 4 Working with Fractals: For the Love of Fractals © 2020 Terrapin Bright Green LLC ENTOMOLOGY & TAXONOMY WHY PEOPLE NEED FRACTALS DEFINING FRACTALS FRACTAL FLUENCY, HEALTH AND THE ALLURE OF NATURAL GEOMETRIES The term fractal comes from the Latin fraˉctus, meaning ‘broken’ and ‘to break, shatter’. The French The experience of fractals has quantifiable health mathematician Benoit Mandelbrot (1924–2010) benefits, including reduced stress, improved cognitive coined this term as a means to describe a ‘never- functioning, enhanced creativity and problem solving, ending pattern’ ubiquitous in nature. The term was heightened appreciation for nature and positive suggested in Mandelbrot’s 1967 book How Long is emotions (see table 3). The benefits of fractals the Coast of Britain: Statistical Self-Similarity and specifically, and of nature more generally, have been Fractional Dimension, and indicates the consecutive shown to occur within minutes, even seconds (Smith magnifications of self-similar patterns. et al., 2020; Lee et al., 2015). As people increasingly find themselves surrounded by urban landscapes, Fractals are self-similar patterns over a range of they become disconnected from nature’s fractals and magnification scales (Fairbanks & Taylor, 2011; its stress-reduction qualities. This nature deficit can Mandelbrot, 1983), resulting in visual stimuli that lead to an unhealthy build-up of stress and the sense are inherently complex and organised. A fractal of placelessness. dimension, abbreviated as ‘D’, is the parameter that indicates fractal complexity or the scaling hierarchy Prolonged stress mobilisation in humans produces a between the patterns at different magnifications. This plethora of harmful consequences, such as increased D value lies across a range from 1.1 to 1.9, with D=1 blood pressure, energy depletion, heightened release and D=2 indicating no fractal properties. For example, of stress hormones, decreased cognitive ability, a smooth line (containing no fractal structure) has and reduced immune function. The World Health a D value of 1, while a completely filled area (also Organization declared stress to be the “Health epidemic containing no fractal structure) has a D value of 2. of the 21st Century” with associated illnesses ranging from depression to schizophrenia (Smith, 2012). Stress- STATISTICAL AND EXACT FRACTALS related illnesses cost countries such as the US over $300 billion (€267.3 billion; £242.4 billion) annually Given the prevalence and variety of fractal patterns (Taylor & Spehar, 2016). In the UK, poor mental health across nature, art and science, this paper focuses costs employers up
Load more

Recommended publications
  • Using Fractal Dimension for Target Detection in Clutter
    KIM T. CONSTANTIKES USING FRACTAL DIMENSION FOR TARGET DETECTION IN CLUTTER The detection of targets in natural backgrounds requires that we be able to compute some characteristic of target that is distinct from background clutter. We assume that natural objects are fractals and that the irregularity or roughness of the natural objects can be characterized with fractal dimension estimates. Since man-made objects such as aircraft or ships are comparatively regular and smooth in shape, fractal dimension estimates may be used to distinguish natural from man-made objects. INTRODUCTION Image processing associated with weapons systems is fractal. Falconer1 defines fractals as objects with some or often concerned with methods to distinguish natural ob­ all of the following properties: fine structure (i.e., detail jects from man-made objects. Infrared seekers in clut­ on arbitrarily small scales) too irregular to be described tered environments need to distinguish the clutter of with Euclidean geometry; self-similar structure, with clouds or solar sea glint from the signature of the intend­ fractal dimension greater than its topological dimension; ed target of the weapon. The discrimination of target and recursively defined. This definition extends fractal from clutter falls into a category of methods generally into a more physical and intuitive domain than the orig­ called segmentation, which derives localized parameters inal Mandelbrot definition whereby a fractal was a set (e.g.,texture) from the observed image intensity in order whose "Hausdorff-Besicovitch dimension strictly exceeds to discriminate objects from background. Essentially, one its topological dimension.,,2 The fine, irregular, and self­ wants these parameters to be insensitive, or invariant, to similar structure of fractals can be experienced firsthand the kinds of variation that the objects and background by looking at the Mandelbrot set at several locations and might naturally undergo because of changes in how they magnifications.
    [Show full text]
  • Title: Fractals Topics: Symmetry, Patterns in Nature, Biomimicry Related Disciplines: Mathematics, Biology Objectives: A. Learn
    Title: Fractals Topics: symmetry, patterns in nature, biomimicry Related Disciplines: mathematics, biology Objectives: A. Learn about how fractals are made. B. Think about the mathematical processes that play out in nature. C. Create a hands-on art project. Lesson: A. Introduction (20 minutes) Fractals are sets in mathematics based on repeated processes at different scales. Why do we care? Fractals are a part of nature, geometry, algebra, and science and are beautiful in their complexity. Fractals come in many types: branching, spiral, algebraic, and geometric. Branching and spiral fractals can be found in nature in many different forms. Branching is seen in trees, lungs, snowflakes, lightning, and rivers. Spirals are visible in natural forms such as hurricanes, shells, liquid motion, galaxies, and most easily visible in plants like flowers, cacti, and Romanesco Figure 1: Romanesco (Figure 1). Branching fractals emerge in a linear fashion. Spirals begin at a point and expand out in a circular motion. A cool demonstration of branching fractals can be found at: http://fractalfoundation.org/resources/what-are-fractals/. Algebraic fractals are based on surprisingly simple equations. Most famous of these equations is the Mandelbrot Set (Figure 2), a plot made from the equation: The most famous of the geometric fractals is the Sierpinski Triangle: As seen in the diagram above, this complex fractal is created by starting with a single triangle, then forming another inside one quarter the size, then three more, each one quarter the size, then 9, 27, 81, all just one quarter the size of the triangle drawn in the previous step.
    [Show full text]
  • Pictures of Julia and Mandelbrot Sets
    Pictures of Julia and Mandelbrot Sets Wikibooks.org January 12, 2014 On the 28th of April 2012 the contents of the English as well as German Wikibooks and Wikipedia projects were licensed under Cre- ative Commons Attribution-ShareAlike 3.0 Unported license. An URI to this license is given in the list of figures on page 143. If this document is a derived work from the contents of one of these projects and the content was still licensed by the project under this license at the time of derivation this document has to be licensed under the same, a similar or a compatible license, as stated in section 4b of the license. The list of contributors is included in chapter Contributors on page 141. The licenses GPL, LGPL and GFDL are included in chapter Licenses on page 151, since this book and/or parts of it may or may not be licensed under one or more of these licenses, and thus require inclusion of these licenses. The licenses of the figures are given in the list of figures on page 143. This PDF was generated by the LATEX typesetting software. The LATEX source code is included as an attachment (source.7z.txt) in this PDF file. To extract the source from the PDF file, we recommend the use of http://www.pdflabs.com/tools/pdftk-the-pdf-toolkit/ utility or clicking the paper clip attachment symbol on the lower left of your PDF Viewer, selecting Save Attachment. After ex- tracting it from the PDF file you have to rename it to source.7z.
    [Show full text]
  • 4.3 Discovering Fractal Geometry in CAAD
    4.3 Discovering Fractal Geometry in CAAD Francisco Garcia, Angel Fernandez*, Javier Barrallo* Facultad de Informatica. Universidad de Deusto Bilbao. SPAIN E.T.S. de Arquitectura. Universidad del Pais Vasco. San Sebastian. SPAIN * Fractal geometry provides a powerful tool to explore the world of non-integer dimensions. Very short programs, easily comprehensible, can generate an extensive range of shapes and colors that can help us to understand the world we are living. This shapes are specially interesting in the simulation of plants, mountains, clouds and any kind of landscape, from deserts to rain-forests. The environment design, aleatory or conditioned, is one of the most important contributions of fractal geometry to CAAD. On a small scale, the design of fractal textures makes possible the simulation, in a very concise way, of wood, vegetation, water, minerals and a long list of materials very useful in photorealistic modeling. Introduction Fractal Geometry constitutes today one of the most fertile areas of investigation nowadays. Practically all the branches of scientific knowledge, like biology, mathematics, geology, chemistry, engineering, medicine, etc. have applied fractals to simulate and explain behaviors difficult to understand through traditional methods. Also in the world of computer aided design, fractal sets have shown up with strength, with numerous software applications using design tools based on fractal techniques. These techniques basically allow the effective and realistic reproduction of any kind of forms and textures that appear in nature: trees and plants, rocks and minerals, clouds, water, etc. For modern computer graphics, the access to these techniques, combined with ray tracing allow to create incredible landscapes and effects.
    [Show full text]
  • Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected]
    University of Massachusetts Amherst ScholarWorks@UMass Amherst Patterns Around Us STEM Education Institute 2017 Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected] Wayne Kermenski Hawlemont Regional School, [email protected] Follow this and additional works at: https://scholarworks.umass.edu/stem_patterns Part of the Biology Commons, Physics Commons, Science and Mathematics Education Commons, and the Teacher Education and Professional Development Commons Welborn, Jennifer and Kermenski, Wayne, "Branching in Nature" (2017). Patterns Around Us. 2. Retrieved from https://scholarworks.umass.edu/stem_patterns/2 This Article is brought to you for free and open access by the STEM Education Institute at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Patterns Around Us by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. Patterns Around Us: Branching in Nature Teacher Resource Page Part A: Introduction to Branching Massachusetts Frameworks Alignment—The Nature of Science • Overall, the key criterion of science is that it provide a clear, rational, and succinct account of a pattern in nature. This account must be based on data gathering and analysis and other evidence obtained through direct observations or experiments, reflect inferences that are broadly shared and communicated, and be accompanied by a model that offers a naturalistic explanation expressed in conceptual, mathematical, and/or mechanical terms. Materials:
    [Show full text]
  • Rendering Hypercomplex Fractals Anthony Atella [email protected]
    Rhode Island College Digital Commons @ RIC Honors Projects Overview Honors Projects 2018 Rendering Hypercomplex Fractals Anthony Atella [email protected] Follow this and additional works at: https://digitalcommons.ric.edu/honors_projects Part of the Computer Sciences Commons, and the Other Mathematics Commons Recommended Citation Atella, Anthony, "Rendering Hypercomplex Fractals" (2018). Honors Projects Overview. 136. https://digitalcommons.ric.edu/honors_projects/136 This Honors is brought to you for free and open access by the Honors Projects at Digital Commons @ RIC. It has been accepted for inclusion in Honors Projects Overview by an authorized administrator of Digital Commons @ RIC. For more information, please contact [email protected]. Rendering Hypercomplex Fractals by Anthony Atella An Honors Project Submitted in Partial Fulfillment of the Requirements for Honors in The Department of Mathematics and Computer Science The School of Arts and Sciences Rhode Island College 2018 Abstract Fractal mathematics and geometry are useful for applications in science, engineering, and art, but acquiring the tools to explore and graph fractals can be frustrating. Tools available online have limited fractals, rendering methods, and shaders. They often fail to abstract these concepts in a reusable way. This means that multiple programs and interfaces must be learned and used to fully explore the topic. Chaos is an abstract fractal geometry rendering program created to solve this problem. This application builds off previous work done by myself and others [1] to create an extensible, abstract solution to rendering fractals. This paper covers what fractals are, how they are rendered and colored, implementation, issues that were encountered, and finally planned future improvements.
    [Show full text]
  • Art on a Cellular Level Art and Science Educational Resource
    Art on a Cellular Level Art and Science Educational Resource Phoenix Airport Museum Educators and Parents, With foundations in art, geometry and plant biology, the objective of this lesson is to recognize patterns and make connections between the inexhaustible variety of life on our planet. This educational resource is geared for interaction with students of all ages to support the understanding between art and science. It has been designed based on our current exhibition, Art on a Cellular Level, on display at Sky Harbor. The questions and activities below were created to promote observation and curiosity. There are no wrong answers. You may print this PDF to use as a workbook or have your student refer to the material online. We encourage educators to expand on this art and science course to create a lesson plan. If you enjoy these activities and would like to investigate further, check back for new projects each week (three projects total). We hope your student will have fun with this and make an art project to share with us. Please send an image of your student’s artwork to [email protected] or hashtag #SkyHarborArts for an opportunity to be featured on Phoenix Sky Harbor International Airport’s social media. Art on a Cellular Level exhibition Sky Harbor, Terminal 4, level 3 Gallery Art is a lens through which we view the world. It can be a tool for storytelling, expressing cultural values and teaching fundamentals of math, technology and science in a visual way. The Terminal 4 gallery exhibition, Art on a Cellular Level, examines the intersections between art and science.
    [Show full text]
  • Turbulence, Fractals, and Mixing
    Turbulence, fractals, and mixing Paul E. Dimotakis and Haris J. Catrakis GALCIT Report FM97-1 17 January 1997 Firestone Flight Sciences Laboratory Guggenheim Aeronautical Laboratory Karman Laboratory of Fluid Mechanics and Jet Propulsion Pasadena Turbulence, fractals, and mixing* Paul E. Dimotakis and Haris J. Catrakis Graduate Aeronautical Laboratories California Institute of Technology Pasadena, California 91125 Abstract Proposals and experimenta1 evidence, from both numerical simulations and laboratory experiments, regarding the behavior of level sets in turbulent flows are reviewed. Isoscalar surfaces in turbulent flows, at least in liquid-phase turbulent jets, where extensive experiments have been undertaken, appear to have a geom- etry that is more complex than (constant-D) fractal. Their description requires an extension of the original, scale-invariant, fractal framework that can be cast in terms of a variable (scale-dependent) coverage dimension, Dd(X). The extension to a scale-dependent framework allows level-set coverage statistics to be related to other quantities of interest. In addition to the pdf of point-spacings (in 1-D), it can be related to the scale-dependent surface-to-volume (perimeter-to-area in 2-D) ratio, as well as the distribution of distances to the level set. The application of this framework to the study of turbulent -jet mixing indicates that isoscalar geometric measures are both threshold and Reynolds-number dependent. As regards mixing, the analysis facilitated by the new tools, as well as by other criteria, indicates en- hanced mixing with increasing Reynolds number, at least for the range of Reynolds numbers investigated. This results in a progressively less-complex level-set geom- etry, at least in liquid-phase turbulent jets, with increasing Reynolds number.
    [Show full text]
  • Fractal Curves and Complexity
    Perception & Psychophysics 1987, 42 (4), 365-370 Fractal curves and complexity JAMES E. CUTI'ING and JEFFREY J. GARVIN Cornell University, Ithaca, New York Fractal curves were generated on square initiators and rated in terms of complexity by eight viewers. The stimuli differed in fractional dimension, recursion, and number of segments in their generators. Across six stimulus sets, recursion accounted for most of the variance in complexity judgments, but among stimuli with the most recursive depth, fractal dimension was a respect­ able predictor. Six variables from previous psychophysical literature known to effect complexity judgments were compared with these fractal variables: symmetry, moments of spatial distribu­ tion, angular variance, number of sides, P2/A, and Leeuwenberg codes. The latter three provided reliable predictive value and were highly correlated with recursive depth, fractal dimension, and number of segments in the generator, respectively. Thus, the measures from the previous litera­ ture and those of fractal parameters provide equal predictive value in judgments of these stimuli. Fractals are mathematicalobjectsthat have recently cap­ determine the fractional dimension by dividing the loga­ tured the imaginations of artists, computer graphics en­ rithm of the number of unit lengths in the generator by gineers, and psychologists. Synthesized and popularized the logarithm of the number of unit lengths across the ini­ by Mandelbrot (1977, 1983), with ever-widening appeal tiator. Since there are five segments in this generator and (e.g., Peitgen & Richter, 1986), fractals have many curi­ three unit lengths across the initiator, the fractionaldimen­ ous and fascinating properties. Consider four. sion is log(5)/log(3), or about 1.47.
    [Show full text]
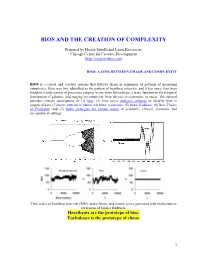
  • Bios and the Creation of Complexity
    BIOS AND THE CREATION OF COMPLEXITY Prepared by Hector Sabelli and Lazar Kovacevic Chicago Center for Creative Development http://creativebios.com BIOS, A LINK BETWEEN CHAOS AND COMPLEXITY BIOS is a causal and creative process that follows chaos in sequences of patterns of increasing complexity. Bios was first identified as the pattern of heartbeat intervals, and it has since then been found in a wide variety of processes ranging in size from Schrodinger’s wave function to the temporal distribution of galaxies, and ranging in complexity from physics to economics to music. This tutorial provides concise descriptions of (1) bios, (2) time series analyses software to identify bios in empirical data, (3) biotic patterns in nature, (4) biotic recursions, (5) biotic feedback, (6) Bios Theory of Evolution, and (7) biotic strategies for human action in scientific, clinical, economic and sociopolitical settings. Time series of heartbeat intervals (RRI), and of biotic and chaotic series generated with mathematical recursions of bipolar feedback. Heartbeats are the prototype of bios. Turbulence is the prototype of chaos. 1 1. BIOS BIOS is an expansive process with chaotic features generated by feedback and characterized by features of creativity. Process: Biotic patterns are sequences of actions or states. Expansive: Biotic patterns continually expand in their diversity and often in their range. This is significant, as natural processes expand, in contrast to convergence to equilibrium, periodic, or chaotic attractors. Expanding processes range from the universe to viruses, and include human populations, empires, ideas and cultures. Chaotic: Biotic series are aperiodic and generated causally; mathematically generated bios is extremely sensitive to initial conditions.
    [Show full text]
  • Synthesis of the Advance in and Application of Fractal Characteristics of Traffic Flow
    Synthesis of the Advance in and Application of Fractal Characteristics of Traffic Flow Final Report Contract No. BDK80 977‐25 July 2013 Prepared by: Lehman Center for Transportation Research Florida International University Prepared for: Research Center Florida Department of Transportation Final Report Contract No. BDK80 977-25 Synthesis of the Advance in and Application of Fractal Characteristics of Traffic Flow Prepared by: Kirolos Haleem, Ph.D., P.E., Research Associate Priyanka Alluri, Ph.D., Research Associate Albert Gan, Ph.D., Professor Lehman Center for Transportation Research Department of Civil and Environmental Engineering Florida International University 10555 West Flagler Street, EC 3680 Miami, FL 33174 Phone: (305) 348-3116 Fax: (305) 348-2802 and Hongtai Li, Graduate Research Assistant Tao Li, Ph.D., Associate Professor School of Computer Science Florida International University 11200 SW 8th Street Miami, FL 33199 Phone: (305) 348-6036 Fax: (305) 348-3549 Prepared for: Research Center State of Florida Department of Transportation 605 Suwannee Street, M.S. 30 Tallahassee, FL 32399-0450 July 2013 DISCLAIMER The opinions, findings, and conclusions expressed in this publication are those of the authors and not necessarily those of the State of Florida Department of Transportation. iii METRIC CONVERSION CHART SYMBOL WHEN YOU KNOW MULTIPLY BY TO FIND SYMBOL LENGTH in inches 25.4 millimeters mm ft feet 0.305 meters m yd yards 0.914 meters m mi miles 1.61 kilometers km mm millimeters 0.039 inches in m meters 3.28 feet ft m meters
    [Show full text]
  • Pattern Formation in Nature: Physical Constraints and Self-Organising Characteristics
    Pattern formation in nature: Physical constraints and self-organising characteristics Philip Ball ________________________________________________________________ Abstract The formation of patterns is apparent in natural systems ranging from clouds to animal markings, and from sand dunes to the intricate shells of microscopic marine organisms. Despite the astonishing range and variety of such structures, many seem to have analogous features: the zebra’s stripes put us in mind of the ripples of blown sand, for example. In this article I review some of the common patterns found in nature and explain how they are typically formed through simple, local interactions between many components of a system – a form of physical computation that gives rise to self- organisation and emergent structures and behaviours. ________________________________________________________________ Introduction When the naturalist Joseph Banks first encountered Fingal’s Cave on the Scottish island of Staffa, he was astonished by the quasi-geometric, prismatic pillars of rock that flank the entrance. As Banks put it, Compared to this what are the cathedrals or palaces built by men! Mere models or playthings, as diminutive as his works will always be when compared with those of nature. What now is the boast of the architect! Regularity, the only part in which he fancied himself to exceed his mistress, Nature, is here found in her possession, and here it has been for ages undescribed. This structure has a counterpart on the coast of Ireland: the Giant’s Causeway in County Antrim, where again one can see the extraordinarily regular and geometric honeycomb structure of the fractured igneous rock (Figure 1). When we make an architectural pattern like this, it is through careful planning and construction, with each individual element cut to shape and laid in place.
    [Show full text]