A Practical Introduction to Computer Architecture
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Z/OS ♦ Z Machines Hardware ♦ Numbers and Numeric Terms ♦ the Road to Z/OS ♦ Z/OS.E ♦ Z/OS Futures ♦ Language Environment ♦ Current Compilers ♦ UNIX System Services
Mainframes The Future of Mainframes Is Now ♦ z/Architecture ♦ z/OS ♦ z Machines Hardware ♦ Numbers and Numeric Terms ♦ The Road to z/OS ♦ z/OS.e ♦ z/OS Futures ♦ Language Environment ♦ Current Compilers ♦ UNIX System Services by Steve Comstock The Trainer’s Friend, Inc. http://www.trainersfriend.com 800-993-8716 [email protected] Copyright © 2002 by Steven H. Comstock 1 Mainframes z/Architecture z/Architecture ❐ The IBM 64-bit mainframe has been named "z/Architecture" to contrast it to earlier mainframe hardware architectures ♦ S/360 ♦ S/370 ♦ 370-XA ♦ ESA/370 ♦ ESA/390 ❐ Although there is a clear continuity, z/Architecture also brings significant changes... ♦ 64-bit General Purpose Registers - so 64-bit integers and 64-bit addresses ♦ 64-bit Control Registers ♦ 128-bit PSW ♦ Tri-modal addressing (24-bit, 31-bit, 64-bit) ♦ Over 140 new instructions, including instructions to work with ASCII and UNICODE strings Copyright © 2002 by Steven H. Comstock 2 z/Architecture z/OS ❐ Although several operating systems can run on z/Architecture machines, z/OS is the premier, target OS ❐ z/OS is the successor to OS/390 ♦ The last release of OS/390 was V2R10, available 9/2000 ♦ The first release of z/OS was V1R1, available 3/2001 ❐ z/OS can also run on G5/G6 and MP3000 series machines ♦ But only in 31-bit or 24-bit mode ❐ Note these terms: ♦ The Line - the 16MiB address limit of MVS ♦ The Bar - the 2GiB limit of OS/390 ❐ For some perspective, realize that 16EiB is... ♦ 8 billion times 2GiB ♦ 1 trillion times 16MiB ❐ The current release of z/OS is V1R4; V1R5 is scheduled for 1Q2004 Copyright © 2002 by Steven H. -

Etir Code Lists
eTIR Code Lists Code lists CL01 Equipment size and type description code (UN/EDIFACT 8155) Code specifying the size and type of equipment. 1 Dime coated tank A tank coated with dime. 2 Epoxy coated tank A tank coated with epoxy. 6 Pressurized tank A tank capable of holding pressurized goods. 7 Refrigerated tank A tank capable of keeping goods refrigerated. 9 Stainless steel tank A tank made of stainless steel. 10 Nonworking reefer container 40 ft A 40 foot refrigerated container that is not actively controlling temperature of the product. 12 Europallet 80 x 120 cm. 13 Scandinavian pallet 100 x 120 cm. 14 Trailer Non self-propelled vehicle designed for the carriage of cargo so that it can be towed by a motor vehicle. 15 Nonworking reefer container 20 ft A 20 foot refrigerated container that is not actively controlling temperature of the product. 16 Exchangeable pallet Standard pallet exchangeable following international convention. 17 Semi-trailer Non self propelled vehicle without front wheels designed for the carriage of cargo and provided with a kingpin. 18 Tank container 20 feet A tank container with a length of 20 feet. 19 Tank container 30 feet A tank container with a length of 30 feet. 20 Tank container 40 feet A tank container with a length of 40 feet. 21 Container IC 20 feet A container owned by InterContainer, a European railway subsidiary, with a length of 20 feet. 22 Container IC 30 feet A container owned by InterContainer, a European railway subsidiary, with a length of 30 feet. 23 Container IC 40 feet A container owned by InterContainer, a European railway subsidiary, with a length of 40 feet. -

Z/OS, Language Environment, and UNIX How They Work Together
The Trainer’s Friend, Inc. 256-B S. Monaco Parkway Telephone: (800) 993-8716 Denver, Colorado 80224 (303) 393-8716 U.S.A. Fax: (303) 393-8718 E-mail: [email protected] Internet: www.trainersfriend.com z/OS, Language Environment, and UNIX How They Work Together The following terms that may appear in these materials are trademarks or registered trademarks: Trademarks of the International Business Machines Corporation: AD/Cycle, AIX, AIX/ESA, Application System/400, AS/400, BookManager, CICS, CICS/ESA, COBOL/370, COBOL for MVS and VM, COBOL for OS/390 & VM, Common User Access, CORBA, CUA, DATABASE 2, DB2, DB2 Universal Database, DFSMS, DFSMSds, DFSORT, DOS/VSE, Enterprise System/3090, ES/3090, 3090, ESA/370, ESA/390, Hiperbatch, Hiperspace, IBM, IBMLink, IMS, IMS/ESA, Language Environment, MQSeries, MVS, MVS/ESA, MVS/XA, MVS/DFP, NetView, NetView/PC, Object Management Group, Operating System/400, OS/400, PR/SM, OpenEdition MVS, Operating System/2, OS/2, OS/390, OS/390 UNIX, OS/400, QMF, RACF, RS/6000, SOMobjects, SOMobjects Application Class Library, System/370, System/390, Systems Application Architecture, SAA, System Object Model, TSO, VisualAge, VisualLift, VTAM, VM/XA, VM/XA SP, WebSphere, z/OS, z/VM, z/Architecture, zSeries Trademarks of Microsoft Corp.: Microsoft, Windows, Windows NT, Windows ’95, Windows ’98, Windows 2000, Windows SE, Windows XP Trademark of Chicago-Soft, Ltd: MVS/QuickRef Trademark of Phoenix Software International: (E)JES Registered Trademarks of Institute of Electrical and Electronic Engineers: IEEE, POSIX Registered Trademark of The Open Group: UNIX Trademark of Sun Microsystems, Inc.: Java Registered Trademark of Linus Torvalds: LINUX Registered Trademark of Unicode, Inc.: Unicode Preface This document came about as a result of writing my first course for UNIX on the IBM mainframe. -
File Organization and Management Com 214 Pdf
File organization and management com 214 pdf Continue 1 1 UNESCO-NIGERIA TECHNICAL - VOCATIONAL EDUCATION REVITALISATION PROJECT-PHASE II NATIONAL DIPLOMA IN COMPUTER TECHNOLOGY FILE Organization AND MANAGEMENT YEAR II- SE MESTER I THEORY Version 1: December 2 2 Content Table WEEK 1 File Concepts... 6 Bit:... 7 Binary figure... 8 Representation... 9 Transmission... 9 Storage... 9 Storage unit... 9 Abbreviation and symbol More than one bit, trit, dontcare, what? RfC on trivial bits Alternative Words WEEK 2 WEEK 3 Identification and File File System Aspects of File Systems File Names Metadata Hierarchical File Systems Means Secure Access WEEK 6 Types of File Systems Disk File Systems File Systems File Systems Transactional Systems File Systems Network File Systems Special Purpose File Systems 3 3 File Systems and Operating Systems Flat File Systems File Systems according to Unix-like Operating Systems File Systems according to Plan 9 from Bell Files under Microsoft Windows WEEK 7 File Storage Backup Files Purpose Storage Primary Storage Secondary Storage Third Storage Out Storage Features Storage Volatility Volatility UncertaintyAbility Availability Availability Performance Key Storage Technology Semiconductor Magnetic Paper Unusual Related Technology Connecting Network Connection Robotic Processing Robotic Processing File Processing Activity 4 4 Technology Execution Program interrupts secure mode and memory control mode Virtual Memory Operating Systems Linux and UNIX Microsoft Windows Mac OS X Special File Systems Journalized File Systems Graphic User Interfaces History Mainframes Microcomputers Microsoft Windows Plan Unix and Unix-like operating systems Mac OS X Real-time Operating Systems Built-in Core Development Hobby Systems Pre-Emptification 5 5 WEEK 1 THIS WEEK SPECIFIC LEARNING OUTCOMES To understand: The concept of the file in the computing concept, field, character, byte and bits in relation to File 5 6 6 Concept Files In this section, we will deal with the concepts of the file and their relationship. -

The 2016 SNIA Dictionary
A glossary of storage networking data, and information management terminology SNIA acknowledges and thanks its Voting Member Companies: Cisco Cryptsoft DDN Dell EMC Evaluator Group Fujitsu Hitachi HP Huawei IBM Intel Lenovo Macrosan Micron Microsoft NetApp Oracle Pure Storage Qlogic Samsung Toshiba Voting members as of 5.23.16 Storage Networking Industry Association Your Connection Is Here Welcome to the Storage Networking Industry Association (SNIA). Our mission is to lead the storage industry worldwide in developing and promoting standards, technologies, and educational services to empower organizations in the management of information. Made up of member companies spanning the global storage market, the SNIA connects the IT industry with end-to-end storage and information management solutions. From vendors, to channel partners, to end users, SNIA members are dedicated to providing the industry with a high level of knowledge exchange and thought leadership. An important part of our work is to deliver vendor-neutral and technology-agnostic information to the storage and data management industry to drive the advancement of IT technologies, standards, and education programs for all IT professionals. For more information visit: www.snia.org The Storage Networking Industry Association 4360 ArrowsWest Drive Colorado Springs, Colorado 80907, U.S.A. +1 719-694-1380 The 2016 SNIA Dictionary A glossary of storage networking, data, and information management terminology by the Storage Networking Industry Association The SNIA Dictionary contains terms and definitions related to storage and other information technologies, and is the storage networking industry's most comprehensive attempt to date to arrive at a common body of terminology for the technologies it represents. -

Engilab Units 2018 V2.2
EngiLab Units 2021 v3.1 (v3.1.7864) User Manual www.engilab.com This page intentionally left blank. EngiLab Units 2021 v3.1 User Manual (c) 2021 EngiLab PC All rights reserved. No parts of this work may be reproduced in any form or by any means - graphic, electronic, or mechanical, including photocopying, recording, taping, or information storage and retrieval systems - without the written permission of the publisher. Products that are referred to in this document may be either trademarks and/or registered trademarks of the respective owners. The publisher and the author make no claim to these trademarks. While every precaution has been taken in the preparation of this document, the publisher and the author assume no responsibility for errors or omissions, or for damages resulting from the use of information contained in this document or from the use of programs and source code that may accompany it. In no event shall the publisher and the author be liable for any loss of profit or any other commercial damage caused or alleged to have been caused directly or indirectly by this document. "There are two possible outcomes: if the result confirms the Publisher hypothesis, then you've made a measurement. If the result is EngiLab PC contrary to the hypothesis, then you've made a discovery." Document type Enrico Fermi User Manual Program name EngiLab Units Program version v3.1.7864 Document version v1.0 Document release date July 13, 2021 This page intentionally left blank. Table of Contents V Table of Contents Chapter 1 Introduction to EngiLab Units 1 1 Overview .................................................................................................................................. -

File Organization & Management
1 UNESCO -NIGERIA TECHNICAL & VOCATIONAL EDUCATION REVITALISATION PROJECT -PHASE II NATIONAL DIPLOMA IN COMPUTER TECHNOLOGY File Organization and Management YEAR II- SE MESTER I THEORY Version 1: December 2008 1 2 Table of Contents WEEK 1 File Concepts .................................................................................................................................6 Bit: . .................................................................................................................................................7 Binary digit .....................................................................................................................................8 Representation ...............................................................................................................................9 Transmission ..................................................................................................................................9 Storage ............................................................................................................................................9 Storage Unit .....................................................................................................................................9 Abbreviation and symbol ............................................................................................................ 10 More than one bit ......................................................................................................................... 11 Bit, trit, -

The 2015 SNIA Dictionary Was Underwritten by the Generous Contributions Of
The 2015 SNIA Dictionary was underwritten by the generous contributions of: If your organization is a SNIA member and is interested in sponsoring the 2016 edition of this dictionary, please contact [email protected]. 4360 ArrowsWest Drive Colorado Springs, CO 80907 719.694.1380 www.snia.org SNIA acknowledges and thanks its Voting Member Companies: Cisco Computerworld Cryptsoft Cygate DDN Dell EMC Emulex Evaluator Group Flexstar Fujitsu Hitachi HP Huawei IBM Intel Macrosan Microsoft NetApp NTP Software Oracle Pure Storage QLogic Samsung Toshiba XIO Voting members as of 3.23.15 Storage Networking Industry Association Your Connection Is Here Welcome to the Storage Networking Industry Association (SNIA). Our mission is to lead the storage industry worldwide in developing and promoting standards, technologies, and educational services to empower organizations in the management of information. Made up of member companies spanning the global storage market, the SNIA connects the IT industry with end-to-end storage and information management solutions. From vendors, to channel partners, to end users, SNIA members are dedicated to providing the industry with a high level of knowledge exchange and thought leadership. An important part of our work is to deliver vendor-neutral and technology-agnostic information to the storage and data management industry to drive the advancement of IT technologies, standards, and education programs for all IT professionals. For more information visit: www.snia.org The Storage Networking Industry Association 4360 ArrowsWest Drive Colorado Springs, Colorado 80907, U.S.A. +1 719-694-1380 The 2015 SNIA Dictionary A glossary of storage networking, data, and information management terminology by the Storage Networking Industry Association The SNIA Dictionary contains terms and definitions related to storage and other information technologies, and is the storage networking industry's most comprehensive attempt to date to arrive at a common body of terminology for the technologies it represents. -
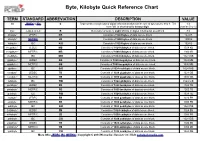
Byte, Kilobyte Quick Reference Chart
Byte, Kilobyte Quick Reference Chart TERM STANDARD ABBREVIATION DESCRIPTION VALUE bit JEDEC & IEC b Represents a single unit of digital information that can be one of two values: 0 or 1. The 1 b term “bit” is shorthand for binary digit. (can be 0 or 1) byte JEDEC & IEC B Generally consists of eight (8) bits of digital information as a block. 8 b kilobyte1 JEDEC KB Consists of 1024 bytes of data as one block. 1024 B kilobyte2 METRIC kB Consists of 1000 bytes of data as one block. 1000 B kibibyte IEC KiB Consists of 1024 bytes of data as one block. 1024 B megabyte1 JEDEC MB Consists of 1024 kilobytes of data as one block. 1024 KB megabyte2 METRIC MB Consists of 1000 kilobytes of data as one block. 1000 kB mebibyte IEC MiB Consists of 1024 kibibytes of data as one block. 1024 KiB gigabyte1 JEDEC GB Consists of 1024 megabytes of data as one block. 1024 MB gigabyte2 METRIC GB Consists of 1000 megabytes of data as one block. 1000 MB gibibyte IEC GiB Consists of 1024 mebibytes of data as one block. 1024 MiB terabyte1 JEDEC TB Consists of 1024 gigabytes of data as one block. 1024 GB terabyte2 METRIC TB Consists of 1000 gigabytes of data as one block. 1000 GB tebibyte IEC TiB Consists of 1024 gibibytes of data as one block. 1024 GiB petabyte1 JEDEC PB Consists of 1024 terabytes of data as one block. 1024 TB petabyte2 METRIC PB Consists of 1000 terabytes of data as one block. 1000 TB pebibyte IEC PiB Consists of 1024 tebibytes of data as one block. -

A+ Guide to Managing & Maintaining Your PC, 8Th Edition
A+ Guide to Managing & Maintaining Your PC, 8th Edition Chapter 4 All About Motherboards Objectives • Learn about the different types and features of motherboards • Learn how to use setup BIOS and physical jumpers to configure a motherboard • Learn how to maintain a motherboard • Learn how to select, install, and replace a motherboard A+ Guide to Managing & Maintaining 2 Your PC, 8th Edition © Cengage Learning 2014 Part 2 Buses and Expansion Slots • Bus – System of pathways used for communication • Carried by bus: – Power, control signals, memory addresses, data • Data and instructions exist in binary – Only two states: on and off • Data path size: width of a data bus – Examples: 8-bit bus has eight wire (lines) to transmit A+ Guide to Managing & Maintaining 3 Your PC, 8th Edition © Cengage Learning 2014 •Bit: A bit is the basic unit of information in computing and digital communications. A bit can have only one of two values, and may therefore be physically implemented with a two-state device. The most common representation of these values are 0 and 1. The term bit is a contraction of binary digit. •Byte: A byte is a unit of digital information in computing and telecommunications that most commonly consists of eight bits. •bps: bit rate, bit per seconds •Hz: (Hertz): It is defined as the number of cycles per second of a periodic phenomenon. The hertz is equivalent to cycles per second. •Radio frequency radiation is usually measured in kilohertz (kHz), megahertz (MHz), or gigahertz (GHz) A+ Guide to Managing & Maintaining 4 Your PC, 8th -

INFORMATION TECHNOLOGY Content
Induction Course for MII Certificate Examination 2017 INFORMATION TECHNOLOGY Content . Part I Archiving Architecture Network Architecture Hardware and Software management . Part II Data mining for operations, quality assurance and planning purposes IT standards Replacement planning Hospital Authority (HA) Future Planning Archiving architecture . Computer Basic . Redundant array of independent disk (RAID) . Hierarchy Storage . Storage Network Technology Computer Basic . 1 byte = 8 bits . 1 kilobyte (K / Kb) = 2^10 bytes = 1,024 bytes . 1 megabyte (M / MB) = 2^20 bytes = 1,048,576 bytes . 1 gigabyte (G / GB) = 2^30 bytes = 1,073,741,824 bytes . 1 terabyte (T / TB) = 2^40 bytes = 1,099,511,627,776 bytes . 1 petabyte (P / PB) = 2^50 bytes = 1,125,899,906,842,624 bytes . 1 exabyte (E / EB) = 2^60 bytes = 1,152,921,504,606,846,976 bytes Computer Basic Multiples of bits Name Standard Name Value (Symbol) SI (Symbol) SI decimal prefixes Binary IEC binary prefixes kilobyte (kB) 103 = 10001 210 kibibyte (KiB) Name Value Name Value (Symbol) (Symbol) 6 2 20 megabyte (MB) 10 = 1000 2 mebibyte (MiB) 3 10 10 kilobit (kbit) 10 2 kibibit (Kibit) 2 9 3 30 gigabyte (GB) 10 = 1000 2 gibibyte (GiB) 6 20 20 megabit (Mbit) 10 2 mebibit (Mibit) 2 9 30 30 12 4 40 gigabit (Gbit) 10 2 gibibit (Gibit) 2 terabyte (TB) 10 = 1000 2 tebibyte (TiB) 12 40 40 15 5 50 terabit (Tbit) 10 2 tebibit (Tibit) 2 petabyte (PB) 10 = 1000 2 pebibyte (PiB) 15 50 50 petabit (Pbit) 10 2 pebibit (Pibit) 2 18 6 60 exabyte (EB) 10 = 1000 2 exbibyte (EiB) 18 60 60 exabit (Ebit) 10 2 exbibit (Eibit) 2 21 7 70 zettabyte (ZB) 10 = 1000 2 zebibyte (ZiB) 21 70 70 zettabit (Zbit) 10 2 zebibit (Zibit) 2 24 8 80 24 80 80 yottabyte (YB) 10 = 1000 2 yobibyte (YiB) yottabit (Ybit) 10 2 yobibit (Yibit) 2 1 word = 2 bytes = 16 bits *Depend on system* Computer Basic . -

Unicorn Documentation Release 1.0.0
unicorn Documentation Release 1.0.0 Philipp Bräutigam, Steffen Brand February 23, 2017 Contents 1 User Guide 3 1.1 Requirements...............................................3 1.2 Installation................................................3 1.3 ConvertibleValue and Unit........................................3 1.3.1 Unit...............................................3 1.3.2 ConvertibleValue........................................4 1.4 Converters................................................4 1.4.1 Converting...........................................4 1.4.2 Mathematical operations....................................5 1.4.3 Nesting.............................................5 1.4.4 Adding your own units.....................................6 1.4.5 Extending converters......................................6 1.4.6 Converter Registry.......................................8 1.4.7 Converter Implementations...................................9 1.5 Contribute................................................ 14 1.6 License.................................................. 15 i ii unicorn Documentation, Release 1.0.0 A framework agnostic library to convert between several units. Contents 1 unicorn Documentation, Release 1.0.0 2 Contents CHAPTER 1 User Guide Requirements • PHP 7.0 or higher • BCMath extension installed and enabled Installation The recommended way to install Unicorn is using Composer. Run the following command in your project directory: composer require xynnn/unicorn This requires you to have Composer installed globally, as explained