Modelling Rankings in R: the Plackettluce Package∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Modelling Rankings in R: the Plackettluce Package
Computational Statistics (2020) 35:1027–1057 https://doi.org/10.1007/s00180-020-00959-3 ORIGINAL PAPER Modelling rankings in R: the PlackettLuce package Heather L. Turner1 · Jacob van Etten2 · David Firth1,3 · Ioannis Kosmidis1,3 Received: 30 October 2018 / Accepted: 18 January 2020 / Published online: 12 February 2020 © The Author(s) 2020 Abstract This paper presents the R package PlackettLuce, which implements a generalization of the Plackett–Luce model for rankings data. The generalization accommodates both ties (of arbitrary order) and partial rankings (complete rankings of subsets of items). By default, the implementation adds a set of pseudo-comparisons with a hypothetical item, ensuring that the underlying network of wins and losses between items is always strongly connected. In this way, the worth of each item always has a finite maximum likelihood estimate, with finite standard error. The use of pseudo-comparisons also has a regularization effect, shrinking the estimated parameters towards equal item worth. In addition to standard methods for model summary, PlackettLuce provides a method to compute quasi standard errors for the item parameters. This provides the basis for comparison intervals that do not change with the choice of identifiability constraint placed on the item parameters. Finally, the package provides a method for model- based partitioning using covariates whose values vary between rankings, enabling the identification of subgroups of judges or settings with different item worths. The features of the package are demonstrated through application to classic and novel data sets. This research is part of cooperative agreement AID-OAA-F-14-00035, which was made possible by the generous support of the American people through the United States Agency for International Development (USAID). -

Kasey Kahne Chevy American Revolution 400 – Richmond International Raceway May 13, 2005
Bud Pole Winner: Kasey Kahne Chevy American Revolution 400 – Richmond International Raceway May 13, 2005 • Kasey Kahne won the NASCAR NEXTEL Cup Series Bud Pole for the Chevy American Revolution 400, lapping Richmond International Raceway in 20.775 seconds at 129.964 mph. Brian Vickers holds the track-qualifying record of 20.772 seconds, 129.983 mph, set May 14, 2004. • This is Kahne’s sixth career Bud Pole in 47 NASCAR NEXTEL Cup Series races. His most recent Bud Pole was last week at Darlington. • This is Kahne’s first top-10 start in three NASCAR NEXTEL Cup Series race at Richmond International Raceway. • Kahne, who also won the Busch Pole for the NASCAR Busch Series race later tonight, became the first driver to sweep weekend poles at Richmond. The last driver to sweep both poles in a weekend was Mark Martin at Rockingham in October 1999. • There has been a different Bud Pole winner in each of the past 11 races at Richmond International Raceway. • Ryan Newman posted the second-quickest qualifying lap of 20.801 seconds, 129.801 mph – and will join Kahne on the front row for the Chevy American Revolution 400. Newman has started from a top-10 starting position in each race this season, the only driver to do so. He has also started from the top-10 in six of his seven races at Richmond, including four times from the front row. • This is the fifth Bud Pole for Dodge in 2005. Chevrolet has four Bud Poles and Ford has two. • Tony Stewart (third) posted his sixth top-10 start in 13 races at Richmond, but his first since May 2003. -

NASCAR Race Number Unofficial Race Results for the Gatorade Duel #1 - Thursday, February 17, 2005 Daytona International Speedway - Daytona Beach, Fla
NASCAR Race Number Unofficial Race Results for the Gatorade Duel #1 - Thursday, February 17, 2005 Daytona International Speedway - Daytona Beach, Fla. - 2.5 Mile High Banked Total Race Length - 60 Laps - 150 Miles Purse: $675,000 Leader Fin Str Car Driver Team Laps Pts Bns Total Award Status Times Laps 1 18 15 Michael Waltrip NAPA Auto Parts Chevrolet 60 $53,199 Running 2 13 2 21 8 Dale Earnhardt Jr. Budweiser Chevrolet 60 $38,188 Running 3 8 * 23 Mike Skinner Bill Davis Racing Dodge 60 $33,188 Running 1 9 4 16 12 Ryan Newman ALLTEL Dodge 60 $28,188 Running 5 5 21 Ricky Rudd Motorcraft Quality Parts Ford 60 $26,188 Running 6 4 97 Kurt Busch Sharpie/IRWIN Industrial Tools Ford 60 $23,788 Running 7 2 24 Jeff Gordon DuPont Chevrolet 60 $22,688 Running 1 28 8 12 42 Jamie McMurray Texaco/Havoline Dodge 60 $21,688 Running 9 11 5 # Kyle Busch Kellogg’s Chevrolet 60 $21,663 Running 10 22 * 00 Kenny Wallace Aaron’s Chevrolet 60 $21,638 Running 11 17 * 33 Kerry Earnhardt Bass Pro Shops Chevrolet 60 $21,613 Running 12 3 * 11 Jason Leffler FedEx Express Chevrolet 60 $21,588 Running 1 2 13 9 16 Greg Biffle National Guard Ford 60 $21,563 Running 14 25 77 # Travis Kvapil Kodak/Jasper Eng. & Trans. Dodge 60 $21,538 Running 15 14 99 Carl Edwards Scotts Ford 60 $21,513 Running 16 15 * 4 Mike Wallace Lucas Oil Chevrolet 60 $21,488 Running 17 19 41 Casey Mears Target Dodge 60 $21,463 Running 18 26 * 92 Stanton Barrett First Trust Portfolios Chevrolet 60 $21,413 Running 19 20 49 Ken Schrader Schwan’s Home Service Dodge 60 $21,388 Running 20 7 45 Kyle Petty Georgia-Pacific/Brawny Dodge 60 $21,363 Running 21 1 88 Dale Jarrett UPS Ford 60 $21,313 Running 1 1 22 13 0 Mike Bliss NetZero/Best Buy Chevrolet 60 $21,288 Running 23 23 * 09 Johnny Sauter Miccosukee Resort Dodge 54 $21,238 Engine 1 6 24 10 9 Kasey Kahne Dodge Dealers/UAW Dodge 52 $21,213 Accident 1 1 25 24 * 66 Hermie Sadler Peak Fitness Ford 46 $21,188 Accident 26 6 38 Elliott Sadler M&M’s Ford 45 $21,163 Transmission 27 28 * 34 Randy LaJoie Mach 1 Inc. -

NASCAR Sprint Cup Series Race Number 6 Unofficial Race Results for the 63Rd Annual Goody's Fast Relief
NASCAR Sprint Cup Series Race Number 6 Unofficial Race Results for the 63Rd Annual Goody's Fast Relief 500 - Sunday, April 1, 2012 Martinsville Speedway - Martinsville, VA - .526 Mile Paved Total Race Length - 515 Laps - 270.89 Miles - Purse: $5,009,303 Leader Driver Fin Str Car Driver Team Laps Pts Bns Rating Winnings Status Tms Laps 1 5 39 Ryan Newman Outback Steakhouse Chevrolet 515 47 4 102.9 $198,808 Running 1 12 2 27 22 AJ Allmendinger Shell Pennzoil Dodge 515 42 89.4 $150,610 Running 3 14 88 Dale Earnhardt Jr. AMP Energy/Diet Mtn. Dew/National Guard Chevrolet 515 42 1 114.7 $116,985 Running 1 3 4 21 17 Matt Kenseth Stephen Siller Tunnel to Towers/Gary Sinise Fdn Ford 515 41 1 99.7 $152,821 Running 1 1 5 13 56 Martin Truex Jr. NAPA Auto Parts Toyota 515 39 98.1 $117,949 Running 6 3 11 Denny Hamlin FedEx Freight Toyota 515 39 1 111.5 $128,101 Running 2 31 7 15 14 Tony Stewart Office Depot / Mobil 1 Chevrolet 515 37 91.8 $133,410 Running 8 19 43 Aric Almirola Smithfield Helping Hungry Homes Ford 515 37 1 90.8 $121,196 Running 1 3 9 7 2 Brad Keselowski Miller Lite Dodge 515 36 1 105.6 $117,455 Running 2 2 10 4 15 Clint Bowyer 5-hour Energy Toyota 515 35 1 113.6 $111,999 Running 1 2 11 28 99 Carl Edwards Fastenal Ford 515 33 74.9 $124,451 Running 12 22 48 Jimmie Johnson myLowes Chevrolet 515 33 1 109.4 $124,071 Running 3 112 13 26 16 Greg Biffle 3M Ford 514 31 78.2 $89,385 Running 14 9 24 Jeff Gordon Drive to End Hunger Chevrolet 514 32 2 133.0 $129,846 Running 6 328 15 12 9 Marcos Ambrose DeWalt Ford 513 29 83.9 $109,668 Running 16 -

Entry List - Numerical Martinsville Speedway Advance Auto Parts 500 Provided by NASCAR Statistical Services - Fri, Apr 8, 2005 @ 3:51 PM Eastern
Entry List - Numerical Martinsville Speedway Advance Auto Parts 500 Provided by NASCAR Statistical Services - Fri, Apr 8, 2005 @ 3:51 PM Eastern Car Driver Driver's Hometown Team Name Owner 1 0 Mike Bliss Milwaukie, OR Net Zero Best Buy Chevrolet Gene Haas 2 * 00 Carl Long Roxboro, NC Buyer's Choice Auto Warranty Chevrolet Raynard McGlynn 3 01 Joe Nemechek Lakeland, FL U.S. Army Chevrolet Nelson Bowers 4 07 Dave Blaney Hartford, OH SKF/Jack Daniel's Chevrolet Richard Childress 5 * 09 Johnny Sauter Necedah, WI Miccosukee Resort Dodge James Finch 6 2 Rusty Wallace St. Louis, MO Miller Lite Dodge Roger Penske 7 * 4 Mike Wallace St. Louis, MO Lucas Oil Chevrolet Larry McClure 8 5 Kyle Busch # Las Vegas, NV Kellogg's Chevrolet Rick Hendrick 9 6 Mark Martin Batesville, AR Viagra Ford Jack Roush 10 * 7 Robby Gordon Orange, CA Harrah's Chevrolet James Smith 11 8 Dale Earnhardt Jr. Kannapolis, NC Budweiser Chevrolet Teresa Earnhardt 12 9 Kasey Kahne Enumclaw, WA Dodge Dealers/UAW Dodge Ray Evernham 13 10 Scott Riggs Bahama, NC Valvoline Chevrolet James Rocco 14 11 Jason Leffler Long Beach, CA FedEx Express Chevrolet J.D. Gibbs 15 12 Ryan Newman South Bend, IN ALLTEL Dodge Roger Penske 16 15 Michael Waltrip Owensboro, KY NAPA Auto Parts Chevrolet Teresa Earnhardt 17 16 Greg Biffle Vancouver, WA Jackson Hewitt Ford Geoffrey Smith 18 17 Matt Kenseth Cambridge, WI DeWalt Power Tools Ford Mark Martin 19 18 Bobby Labonte Corpus Christi, TX Interstate Batteries Chevrolet Joe Gibbs 20 19 Jeremy Mayfield Owensboro, KY Dodge Dealers/UAW Dodge Ray Evernham -

Madison International Speedway Past Event / Series Winners / Track Records
Madison International Speedway Past Event / Series Winners / Track Records Super Late Model Triple Crown Challenge Champions 2018- Austin Nason 2017- Dan Fredrickson 2016- Casey Johnson 2015- Jeremy Miller 2014- Chris Wimmer 2013- Casey Johnson 2012- Nathan Haseleu Super Late Model Triple Crown Challenge Race Winners 2018- Ty Majeski, Johnny Sauter 2017- Rich Bickle Jr., Paul Shafer Jr., Dan Fredrickson 2016- Ty Majeski, Jeremy Miller 2015- Ty Majeski-2, Casey Johnson 2014- Dave Feiler, Matt Kenseth, Chris Wimmer 2013- Travis Sauter (2), Rich Bickle Jr., Casey Johnson 2012- Travis Sauter (5), Nathan Haseleu (3) *Note= double features ARCA Midwest Tour Joe Shear Classic 2019- Bubba Pollard 2018- Austin Nason 2017- Andrew Morrissey 2016- Ty Majeski 2015- Johnny Sauter 2014- Nathan Haseleu 2013- Travis Sauter 2012- Andrew Morrissey 2011- Ross Kenseth 2010- Steve Carlson 2009- Nathan Haseleu ARCA Racing Series 2019- Chandler Smith 2018- Chandler Smith 2017- Austin Theriault 2016- Josh Williams 2015- No Race 2014- Justin Boston 2013- Kyle Benjamin 2012- Chris Buescher 2011- Alex Bowman 1973- Bruce Gould 1971- Tom Bowsher 1970- Ramo Stott Big 8 Late Models 2019- Dale Nottestad 2018- Michael Bilderback 2017- Jeremy Miler 2016- Jeremy Miller 2015- Austin Nason 2014- Jon Reynolds Jr. 2013- Dale Nottestad 2012- Zack Riddle 2011- Zack Riddle and Steve Rubeck 2010- Dale Nottestad and John Baumeister Jr. 2009- Ross Kenseth (2) 2008- Jeremy Miller and Ryan Carlson 2007- Brian Hoppe and Brady Liddle 2006- Jeremy Miller 2005- Tim Sauter Howie Lettow Classic 2019- Ty Majeski 2018- Rained Out 2017- Paul Shafer Jr. 2016 Rained Out 2015 Ty Majeski 2014 Erik Jones* 2013 Kyle Busch* 2012 Travis Sauter* *Event held at The Milwaukee Mile American Speed Association (ASA) 2004 Tim Sauter 2003 Butch Miller 2002 Steve Carlson 2001 Robbie Pyle 2000 Gary St. -

Poucjhli^Sie Journal^ Poughkeepsie, N.Y
Poucjhli^sie Journal^ Poughkeepsie, N.Y. AFFIDAVIT OF PUBLICATION NEW YORK STATE PUBLIC SERVICE COMMISSION February 7, 2006 State of New York NOTICE OF PUBLIC STATEMENT County of Dutchess HEARINGS ON CENTRAL HUDSON City of Poughkeepsie GAS & ELECTRIC CORPORATION'S PROPOSAL TO INCREASE ELECTRIC AND GAS RATES Rita Lombardi ; of the City of poughkeepsie! • The New York State Public Service Commission seeks public comments regarding Central Hudson- Gas & Dutchess County, New York, being duly sworn, says that at Electric Corporation's July 29,2005 request to increase its the several times hereinafter mentioned she was and still is annual electric and gas revenues. According to Central Hudson's July 2005 filing with the Commission, the pro- the Principal Clerk of the Poughkeepsie Newspapers Division posed rate revisions are designed to produce an overall of Gannett Satellite Information Network, Inc., publisher of increase of about $52.8 million or 13% in annual electric revenues and about $18.1 million or 15% in annual gas . the POUGHKEEPSIE JOURNAL, a newspaper printed and revenues. The proposed increases have been suspended published every day in the year 2006 in the city of through June 26, 2006. The company's request may be Poughkeepsie, Dutchess County, New York, and that the approved, modified, or rejected by the Commission, in an whole or in part. ne«d NOTICE was duly published in the said newspaper Public statement hearings, will be held as follows: •or weeks successively, in each week, commencing Poughkeepsie Monday, March 13, 2006 on the g^ f 3:00'p.m. day 0 Dutchess County Office Building Legislative Chambers,, 6th floor 2005 and. -
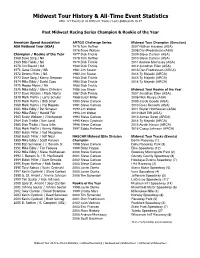
Midwest Tour History & All-Time Event Statistics
Midwest Tour History & All-Time Event Statistics After 121 Events at 20 Different Tracks / Last Updated 06.18.17 Past Midwest Racing Series Champion & Rookie of the Year American Speed Association ARTGO Challenge Series Midwest Tour Champion (Sanction) ASA National Tour (ASA) 1975 Tom Reffner 2007 Nathan Haseleu (ASA) 1976 Dave Watson 2008 Dan Fredrickson (ASA) Champion / Rookie of the Year 1977 Dick Trickle 2009 Steve Carlson (ASA) 1968 Dave Sorg / NA 1978 Tom Reffner 2010 Steve Carlson (ASA) 1969 Bob Fields / NA 1979 Dick Trickle 2011 Andrew Morrissey (ASA) 1970 Jim Blount / NA 1980 Dick Trickle 2012 Jonathan Eilen (ASA) 1971 Gene Christe / NA 1981 Jim Sauter 2013 Dan Fredrickson (ARCA) 1972 Dennis Miles / NA 1982 Jim Sauter 2014 Ty Majeski (ARCA) 1973 Dave Sorg / Kenny Simpson 1983 Dick Trickle 2015 Ty Majeski (ARCA) 1974 Mike Eddy / David Cope 1984 Dick Trickle 2016 Ty Majeski (ARCA) 1975 Moose Myers / NA 1985 Dick Trickle 1976 Mike Eddy / Glenn Ohlmann 1986 Joe Shear Midwest Tour Rookie of the Year 1977 Dave Watson / Mark Martin 1987 Dick Trickle 2007 Jonathan Eilen (ASA) 1978 Mark Martin / Larry Schuler 1988 Butch Miller 2008 Nick Murgic (ASA) 1979 Mark Martin / Bob Strait 1990 Steve Carlson 2009 Jacob Goede (ASA) 1980 Mark Martin / Hyl Magoon 1991 Steve Carlson 2010 Ross Kenseth (ASA) 1981 Mike Eddy / Pat Schauer 1992 Jim Weber 2011 Skylar Holzhausen (ASA) 1982 Mike Eddy / Harold Fair 1993 Jim Weber 2012 Matt Tifft (ASA) 1983 Rusty Wallace / J Kurkowski 1994 Steve Carlson 2013 James Swan (ARCA) 1984 Dick Trickle / Ken Lund 1995 Kevin Cywinski 2014 Ty Majeski (ARCA) 1985 Dick Trickle / Russ Urlin 1996 Steve Carlson 2015 Austin Nason (ARCA) 1986 Mark Martin / Kenny Wallace 1997 Eddie Hoffman 2016 Casey Johnson (ARCA) 1987 Butch Miller / Ted Musgrave 1988 Butch Miller / Jeff Neal NASCAR Midwest Elite Division Midwest Tour Tracks (Events) 1989 Mike Eddy / Scott Hansen Champion Berlin Raceway (1) 1990 Bob Senneker / J. -

Post-Race Report
Loop Data Statistics Post-Race Report Sprint Showdown May 16, 2009 Provided by STATS LLC and NASCAR - Saturday, May 16, 2009 NASCAR Sprint Cup Series Average Running Position Sum of driver position on each lap - divided by the laps run in the race. Sprint Showdown Lowe's Motor Speedway May 16, 2009 Car Finish Average Rk. Number Driver Team Pos. Place 1 12 David Stremme No. 12 Penske 3 1.725 2 77 Sam Hornish Jr. Mobil 1 1 2.225 3 1 Martin Truex Jr. Bass Pro Shops / National Wild Turkey Federation 6 4.100 4 66 Dave Blaney Red Rocks Cafe 11 5.975 5 00 David Reutimann Aaron's Dream Machine 4 6.175 6 44 AJ Allmendinger Hunt Brothers Pizza 7 7.075 7 26 Jamie McMurray Crown Royal 2 7.325 8 6 David Ragan UPS 8 7.675 9 42 Juan Pablo Montoya Target 12 8.875 10 47 Marcos Ambrose Kingsford / Clorox 10 9.900 11 20 Joey Logano The Home Depot 5 10.750 12 98 Paul Menard Johns Manville / Menards 17 12.875 13 7 Robby Gordon Jim Beam Operation Home Front 9 14.475 14 71 David Gilliland CompUSA.com 15 15.600 15 21 Bill Elliott Motorcraft 16 16.575 16 43 Reed Sorenson McDonald's / McCafe 18 16.675 17 07 Casey Mears Jack Daniel's 13 16.875 18 55 Michael Waltrip NAPA Auto Parts 14 18.325 19 82 Scott Speed Red Bull 19 19.450 20 87 Joe Nemechek Nemco Motorsports 20 20.875 21 13 Max Papis GEICO 21 21.225 22 37 Mike Wallace Long John Silver's 26 22.075 23 51 Dexter Bean Livewire Energy 23 23.425 24 36 Scott Riggs 25 24.050 25 41 J.J. -

Post-Race Report
Loop Data Statistics Post-Race Report Nextel Open May 21, 2005 Provided by STATS LLC and NASCAR - Thursday, January 22, 2009 NASCAR Nextel Cup Series Average Running Position Sum of driver position on each lap - divided by the laps run in the race. Nextel Open Lowe's Motor Speedway May 21, 2005 Car Finish Average Rk. Number Driver Team Pos. Place 1 0 Mike Bliss NetZero/Best Buy 2 1.467 2 77 Travis Kvapil Kodak/Jasper Engines 3 1.800 3 25 Brian Vickers GMAC/ditech.com 1 4.067 4 41 Casey Mears Target 6 5.167 5 49 Ken Schrader Red Barron Pizza 9 5.367 6 5 Kyle Busch Kellogg's 4 7.333 7 7 Robby Gordon Fruit of the Loom 7 7.667 8 21 Ricky Rudd Motorcraft Genuine Parts 8 7.900 9 1 Martin Truex Jr. Bass Pro Shops 10 8.567 10 32 Bobby Hamilton Jr. Tide 5 10.833 11 43 Jeff Green Cheerios/Betty Crocker 12 11.300 12 22 Scott Wimmer Caterpillar 15 13.100 13 37 Kevin Lepage Underdog 19 14.200 14 31 Jeff Burton Cingular Wireless 11 14.333 15 42 Jamie McMurray Texaco/Havoline 14 14.400 16 50 Jimmy Spencer Arnold Development Companies 16 15.167 17 07 Dave Blaney Jack Daniel's Country Cocktails 17 15.300 18 40 Sterling Marlin Coors Light 13 15.600 19 4 Mike Wallace Wide Open Energy Drink 18 18.933 20 60 Derrike Cope Year One 21 19.833 21 45 Kyle Petty Georgia-Pacific/Brawny 22 21.100 22 36 Boris Said Centrix Financial 23 21.733 23 66 Hermie Sadler Peak Fitness 20 22.267 24 11 Jason Leffler FedEx Ground 24 24.133 25 92 Eric McClure 26 24.400 26 27 Kirk Shelmerdine Freddie B's 25 25.233 27 89 Morgan Shepherd Red Line Oil/Racing with Jesus 27 26.900 28 10 Scott Riggs Valvoline 28 27.900 Provided by STATS LLC and NASCAR - Thursday, January 22, 2009 NASCAR Nextel Cup Series Box Score Nextel Open Lowe's Motor Speedway May 21, 2005 Green Flag Passes for the Lead: 9 Green % of # of % of % of Car Mid 3 Laps High Low Avg Pass Green Times Quality Quality Fastest Laps in Laps in Laps Laps Total Driver No. -

Lead Fin Pos Driver Team Laps Pts Stg 1 Pos Status Tms Laps Str Pos
MONSTER ENERGY NASCAR CUP SERIES OFFICIAL RACE REPORT No. 34 14TH ANNUAL AAA TEXAS 500 TEXAS MOTOR SPEEDWAY Fort Worth, TX - November 4, 2018 1.5-mile Paved Tri-oval 337 Laps - 505.5 Miles TIME OF RACE: 3 hours, 21 minutes, 27 seconds AVERAGE SPEED: 150.558 mph MARGIN OF VICTORY: 0.447 second(s) Fin Str Car Stg 1 Stg 2 Lead Playoff Pos Pos No Driver Team Laps Pos Pos Pts Status Tms Laps Pts 1 3 4 Kevin Harvick Mobil 1 Ford 337 1 1 60 Running 5 177 2 1 12 Ryan Blaney Accella/Carlisle Ford 337 4 2 51 Running 3 40 3 8 22 Joey Logano AAA Insurance Ford 337 6 5 45 Running 4 54 4 12 20 Erik Jones Sport Clips Toyota 337 3 7 45 Running 5 22 42 Kyle Larson DC Solar Chevrolet 337 32 Running 6 16 9 Chase Elliott Kelley Blue Book Chevrolet 337 9 10 34 Running 7 7 41 Kurt Busch State Water Heaters Ford 337 2 8 42 Running 8 4 10 Aric Almirola Smithfield Spirals Ford 337 10 6 35 Running 9 13 78 Martin Truex Jr Bass Pro Shops/5-hour ENERGY Toyota 337 5 3 42 Running 10 26 3 Austin Dillon Dow NORKOOL Chevrolet 337 27 Running 11 17 17 Ricky Stenhouse Jr Fastenal Ford 337 26 Running 12 5 2 Brad Keselowski Wurth Ford 337 4 32 Running 1 50 13 11 21 Paul Menard Menards/Cardell Ford 337 8 27 Running 14 18 88 Alex Bowman Axalta Chevrolet 337 23 Running 1 3 15 23 48 Jimmie Johnson Lowe's for Pros Chevrolet 337 22 Running 2 11 16 9 24 William Byron # Hendrick Autoguard Chevrolet 337 21 Running 17 10 18 Kyle Busch M&M's Toyota 337 7 24 Running 18 14 31 Ryan Newman Caterpillar Next Gen Excavator Chevrolet 335 19 Running 19 20 1 Jamie McMurray Sherwin-Williams Chevrolet -

Race Results
Xfinity Series Race Number 27 Race Results for the 39th Annual Go Bowling 250 - Friday, September 20, 2019 Richmond Raceway - Richmond, VA - 0.75 - Mile Paved Total Race Length - 250 Laps - 187.5 Miles Stage 1 Stage 2 Playoff Fin Str Car Driver Team Laps Pos Pos Pts Status Tms Laps Pts 1 4 20 Christopher Bell (P) Rheem Toyota 250 1 1 60 Running 2 238 7 2 1 22 Austin Cindric (P) MoneyLion Ford 250 2 5 50 Running 2 8 3 12 00 Cole Custer (P) GoBowling Ford 250 5 2 49 Running 4 2 7 Justin Allgaier (P) BRANDT Professional Agriculture Chevrolet 250 10 3 42 Running 5 5 98 Chase Briscoe # (P) Ford Performance Ford 250 9 7 38 Running 6 6 18 Harrison Burton(i) DEX Imaging Toyota 250 9 0 Running 7 8 9 Noah Gragson # (P) Superior Essex Chevrolet 250 3 6 43 Running 8 15 8 Zane Smith PatientPop Chevrolet 250 29 Running 9 10 1 Michael Annett (P) Pilot Flying J Chevrolet 250 4 4 42 Running 10 3 2 Tyler Reddick (P) Gimme Radio Chevrolet 250 27 Running 11 11 19 Brandon Jones (P) Freightliner Toyota 250 8 29 Running 1 4 12 13 39 Ryan Sieg (P) Larry's Hard Lemonade Chevrolet 250 8 28 Running 13 26 90 Dillon Bassett Bassett Gutters and More Chevrolet 249 24 Running 14 16 21 Joe Graf Jr. Eat Sleep Race Chevrolet 249 23 Running 15 38 23 John Hunter Nemechek # Safeway Chevrolet 249 7 10 27 Running 16 14 51 Jeremy Clements TopGolf Chevrolet 249 21 Running 17 7 11 Justin Haley # (P) LeafFilter Gutter Protection Chevrolet 249 6 25 Running 18 18 07 Ray Black II ISOKERNFrplcsChmnys/ScbaLife Chev 248 19 Running 19 19 01 Ryan Repko The McLain Group Chevrolet 248 18 Running 20 30 35 Joey Gase Donate Life Virginia Toyota 248 17 Running 21 34 78 JJ Yeley BringYourBible.org Toyota 247 16 Running 22 9 08 Gray Gaulding Panini Chevrolet 247 15 Running 23 28 36 Josh Williams Harkin Construction Chevrolet 247 14 Running 24 35 93 Hermie Sadler Virginia Lottery Chevrolet 247 13 Running 25 29 52 David Starr HollywdAutoSls/PrfrdTowng Chev 247 12 Running 26 20 61 Chad Finchum MBM Motorsports Toyota 246 11 Running 27 32 0 Garrett Smithley Trophy Tractor Chevrolet 246 10 Running 28 23 99 Matt Mills J.F.