Durham E-Theses
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Historiography and Narratives of the Later Tang (923-936) and Later Jin (936-947) Dynasties in Tenth- to Eleventh- Century Sources
Historiography and Narratives of the Later Tang (923-936) and Later Jin (936-947) Dynasties in Tenth- to Eleventh- century Sources Inauguraldissertation zur Erlangung des Doktorgrades der Philosophie an der Ludwig‐Maximilians‐Universität München vorgelegt von Maddalena Barenghi Aus Mailand 2014 Erstgutachter: Prof. Dr. Hans van Ess Zweitgutachter: Prof. Tiziana Lippiello Datum der mündlichen Prüfung: 31.03.2014 ABSTRACT Historiography and Narratives of the Later Tang (923-36) and Later Jin (936-47) Dynasties in Tenth- to Eleventh-century Sources Maddalena Barenghi This thesis deals with historical narratives of two of the Northern regimes of the tenth-century Five Dynasties period. By focusing on the history writing project commissioned by the Later Tang (923-936) court, it first aims at questioning how early-tenth-century contemporaries narrated some of the major events as they unfolded after the fall of the Tang (618-907). Second, it shows how both late- tenth-century historiographical agencies and eleventh-century historians perceived and enhanced these historical narratives. Through an analysis of selected cases the thesis attempts to show how, using the same source material, later historians enhanced early-tenth-century narratives in order to tell different stories. The five cases examined offer fertile ground for inquiry into how the different sources dealt with narratives on the rise and fall of the Shatuo Later Tang and Later Jin (936- 947). It will be argued that divergent narrative details are employed both to depict in different ways the characters involved and to establish hierarchies among the historical agents. Table of Contents List of Rulers ............................................................................................................ ii Aknowledgements .................................................................................................. -

1 Regulatory and Policy Framework for Religion During The
1 FREEDOM OF RELIGION Regulatory and Policy Framework for Religion During the Commission’s 2015 reporting year, the Chinese gov- ernment and Communist Party continued to restrict freedom of re- ligion in China. China’s Constitution guarantees ‘‘freedom of reli- gious belief’’ 1 but limits protection of religious activities to ‘‘normal religious activities.’’ 2 This narrow protection contravenes inter- national human rights standards. Article 18 of the Universal Dec- laration of Human Rights (UDHR) and Article 18 of the Inter- national Covenant on Civil and Political Rights (ICCPR)—the lat- ter of which China has signed 3 and stated its intent to ratify 4— recognize not only an individual’s right to adopt a religion or belief, but also the freedom to manifest one’s religion in ‘‘worship, observ- ance, practice and teaching.’’ 5 The Chinese government continued to recognize only five reli- gions: Buddhism, Catholicism, Islam, Protestantism, and Taoism. The 2005 Regulations on Religious Affairs (RRA) require groups wishing to practice these religions to register with the government and subject such groups to government controls.6 The government and Party control religious affairs mainly through the State Ad- ministration for Religious Affairs (SARA) and lower level religious affairs bureaus under the State Council,7 the Party Central Com- mittee United Front Work Department (UFWD),8 and the five ‘‘pa- triotic’’ religious associations—the Buddhist Association of China (BAC), the Catholic Patriotic Association of China (CPA), the Is- lamic -

Your Paper's Title Starts Here
International Conference on Architectural Engineering and Civil Engineering (AECE 2016) Advances in Engineering Research Volume 72 Shanghai, China 9 – 11 December 2016 Editors: Lian-Cheng Dong Pei-Hsing Huang Togay Ozbakkaloglu ISBN: 978-1-5108-3600-6 Printed from e-media with permission by: Curran Associates, Inc. 57 Morehouse Lane Red Hook, NY 12571 Some format issues inherent in the e-media version may also appear in this print version. Copyright© (201 7) by Atlantis Press All rights reserved. http://www.atlantis-press.com/php/pub.php?publication=aece-16 Printed by Curran Associates, Inc. (2017) For permission requests, please contact the publisher: Atlantis Press Amsterdam / Paris Email: [email protected] Additional copies of this publication are available from: Curran Associates, Inc. 57 Morehouse Lane Red Hook, NY 12571 USA Phone: 845-758-0400 Fax: 845-758-2633 Email: [email protected] Web: www.proceedings.com TABLE OF CONTENTS ARCHITECTURE RISK FACTORS OF POST-EARTHQUAKE FIRE FOR CONSTRUCTIONS USING THE ANALYTIC HIERARCHY PROCESS APPROACH........................................................................................................1 Hsiaomei Lin, Chingyuan Lin, Juicheng Ko, Yushiang Wu EFFECT OF THE PARTICLE SIZE DISTRIBUTION OF FLY ASH ON THE PORE STRUCTURE OF LOW-TEMPERATURE CONCRETE .........................................................................................................................5 Jun Liu, Xianzhong Qiu, Yahui Zhang PERFORMANCE AND APPLICATION ANALYSIS OF EXISTING ENERGY-SAVING -

October 2015 Newsletter
CHINESE CULTURAL STUDIES CENTER OCTOBER 2015 CHINESE CULTURAL EVENTS AROUND HONG KONG Selected dates from 20 Nov- 5 Dec 2015 Cantonese Opera: Investigation to Redress a Wrong (re-run) Dierent venue depending on date 粤劇《搜證雪冤》(重演) Playright/Artistic Director: Sun Kim-long. Story: Wang Yingcai, who rescued Prince Gong, has been betrayed and his family has suffered. He seeks to redress the wrong done to him. 1 November 2015 Concert by Hong Kong YWCA Chinese Orchestra China Archaeology Lecture Series, October 9, 2014- Chinese University of Hong Kong campus. From left to Tsuen Wan Town Hall right: Prof. Celine Lai (CUMT, CUHK); Carrie Cox (CCSC), Prof. Zhang Chang Ping (Wuhan University); Prof. Jing Zhong 香港女青中樂團「吹彈拉打」音樂會 Wei (Jilin University); Oi Ling Chiang (CCSC); Mr. Liu Hai Wang (HPICRA); Prof. Huo Wei (Sichuan University), Prof. Cheung Chin Hung (CUMT, CUHK); Mr. Chu Xiao Long (HPICRA); Prof. Zhao Jun Jie (Jilin University) Hong Kong YWCA Chinese Orchestra is an interest group established in 1962 under the Hong Kong YWCA, and is one of the oldest DEAR FRIENDS, Chinese orchestras in Hong Kong. The orchestra regularly performs to the general public different We hope this newsletter finds you well! A couple of important things styles of Chinese folk music. have taken place since the last issue of newsletter, and we hope you’ll 29 November 2015 enjoy reading about our updates here. “Pipa Chun Qiu”- Concert by Hong Kong Music Lover Chinese Orchestra The China Archaeology Lecture Series was a great success- the Tsuen Wan Town Hall presenters shared findings in their various areas of research and focus, 「琵琶春秋」 - 香港愛樂民樂團 opening the eyes of the attendees to the many wonderful archaeologi- Presented by Hong Kong Music Lover Chiense cal works currently being undertaken in China. -

Qi-Ju Design Knowledge: an Historical and Methodological Exploration of Classical Chinese Texts on Everyday Objects
Copyright Undertaking This thesis is protected by copyright, with all rights reserved. By reading and using the thesis, the reader understands and agrees to the following terms: 1. The reader will abide by the rules and legal ordinances governing copyright regarding the use of the thesis. 2. The reader will use the thesis for the purpose of research or private study only and not for distribution or further reproduction or any other purpose. 3. The reader agrees to indemnify and hold the University harmless from and against any loss, damage, cost, liability or expenses arising from copyright infringement or unauthorized usage. IMPORTANT If you have reasons to believe that any materials in this thesis are deemed not suitable to be distributed in this form, or a copyright owner having difficulty with the material being included in our database, please contact [email protected] providing details. The Library will look into your claim and consider taking remedial action upon receipt of the written requests. Pao Yue-kong Library, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong http://www.lib.polyu.edu.hk QJ-JU DESIGN KNOWLEDGE: AN HISTORICAL AND METHODOLOGICAL EXPLORATION OF CLASSICAL CHINESE TEXTS ON EVERYDAY OBJECTS TANG WEICHEN Ph.D The Hong Kong Polytechnic University 2013 The Hong Kong Polytechnic University School of Design Qi-ju Design Knowledge: An Historical and Methodological Exploration of Classical Chinese Texts on Everyday Objects Tang Weichen A thesis submitted in partial fulfillment of the requirements for the Degree of Doctor of Philosophy December 2010 ABSTRACT This thesis responds to the repeated calls in the Chinese design field for the creation of modern Chinese-style products and for the establishment of a distinctly indigenous system for the theoretical and methodological study of ancient Chinese products. -

Les Origines Et Les Transformations Institutionnelles Du Royaume De Shu (907-965)
LES ORIGINES ET LES TRANSFORMATIONS INSTITUTIONNELLES DU ROYAUME DE SHU (907-965) Par Sébastien Rivest Département d‟études est-asiatiques Université McGill, Montréal Mémoire présenté à l‟Université McGill en vue de l‟obtention du grade de Maîtrise ès arts (M.A.) Septembre 2010 © Sébastien Rivest, 2010 TABLE DES MATIÈRES : Abstract/Résumé ii Remerciements iii Conventions iv Abréviations v Introduction 0.1 La transition Tang-Song 1 0.2 Les rapports État-société 4 0.3 Les enjeux historiographiques 9 I Le contexte historique 16 1.1 L‟érosion de l‟aristocratie (763-875) 16 1.2 Le temps des rébellions et la destruction de l‟aristocratie (860-907) 29 1.3 Les Cinq dynasties et le nouvel ordre politique (907-960) 36 II Le Royaume de Shu antérieur (907-925) 49 2.1 Les loyalistes en exil à Chengdu 56 2.2 Le loyalisme de l‟armée Zhongwu 65 2.3 La morphologie d‟un État loyaliste 79 a) Les Trois départements 81 b) Le Secrétariat impérial 83 c) La Chancellerie impériale 92 d) Le Département des affaires d‟État 98 e) La dichotomie entre lettrés de cour et militaires 102 III Le Royaume de Shu postérieur (934-965) 108 3.1 Les associés de Meng Zhixiang et les régents de son successeur 113 3.2 Le développement des préfectures 129 3.3 Une bureaucratie renouvelée, un État transformé 136 Conclusion 143 Bibliographie sélective 151 i ABSTRACT : This thesis is a regional case study on the metamorphosis of state institutions at a time when China went through an important period of political division. -
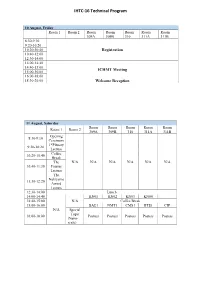
IHTC-16 Technical Program
IHTC-16 Technical Program 10 August, Friday Room 1 Room 2 Room Room Room Room Room 309A 309B 310 311A 311B 8:30-9:10 9:20-10:20 10:20-10:40 Registration 10:40-12:00 12:30-14:00 14:00-14:40 14:40-15:00 ICHMT Meeting 15:00-16:00 16:00-18:00 18:30-20:00 Welcome Reception 11 August, Saturday Room Room Room Room Room Room 1 Room 2 309A 309B 310 311A 311B Opening 8:30-9:10 Ceremony 1*Plenary 9:20-10:20 Lecture Coffee 10:20-10:40 Break The N/A N/A N/A N/A N/A N/A 10:40-11:30 Fourier Lecture The Nukiyama 11:30-12:20 Award Lecture 12:30-14:00 Lunch 14:00-14:40 KN01 KN02 KN03 KN04 14:40-15:00 N/A Coffee Break 15:00-16:00 BAE1 NMT1 CMS1 HTE1 CIP N/A Special Topic 16:00-18:00 Posters Posters Posters Posters Posters (Nano- scale) 12 August, Sunday Room Room Room Room Room Room 2 309A 309B 310 311A 311B 8:30-9:10 KN05 KN06 KN07 KN08 9:20-10:20 COV1 COD1 TPM1 RAC HTE2 10:20-10:40 Coffee Break 10:40-12:20 Posters Posters Posters Posters Posters N/A 12:30-14:00 Lunch 14:00-14:40 KN09 KN10 KN11 KN12 KN13 14:40-15:00 Coffee Break 15:00-16:00 BAE2 NMT2 NEE1 CTM1 COV2 Special topic 16:00-18:00 Posters Posters Posters Posters Posters (Energy Storage) 13 August, Monday Room Room Room Room Room 309A 309B 310 311A 311B 8:30-9:10 KN14 KN15 KN16 KN17 9:20-10:20 ECL MPF1 CMS2 BMA COD2 10:20-10:40 Coffee Break 10:40-12:20 Posters Posters Posters Posters Posters 12:30-14:00 Lunch 14:00-14:40 14:40-15:00 Break 15:00-16:00 AIHTC committee meeting 16:00-18:00 18:30-20:00 14 August, Tuesday Room Room Room Room Room Room 2 309A 309B 310 311A 311B 8:30-9:10 KN18 KN19 KN20 -

Text and Its Cultural Interpretation
TEXT AND ITS CULTURAL INTERPRETATION I. Alimov MORE ABOUT SUN GUANG-XIAN AND BEI MENG SUO YAN1* There is very little information remaining about Sun “Generations [of the Song family] worked on the Guang-xian (孫光憲, 895?—968, second name land, but only Guang-xian began studying diligently Meng-wen 孟文, pen-name Baoguang-zi 葆光子); from a young age”, even his exact date of birth is not known [1]. His life- time came at the very end of the Tang rule, the period it is stated in Song dynastic history. Sun Guang-xian of the Five Dynasties and the first years of the Song was the first in his family who resolved to escape from dynasty. Information on where Sun came from is also poverty, and set his mind on science, book-learning, contradictory: well-known Song bibliophile Chen arts and achieved considerable results in these areas. Zheng-sun (陳振孫, 1190—1249) wrote in his bibliog- He followed the path of an official: he successfully raphy [2] that Sun Guang-xian was originally from passed the examinations and joined the public service Guiping in the region of Lingzhou (in the north-east and his first appointment the post of administrative part of what now is the Renshouxian district of assistant of his home region of Lingzhou [6]. The au- Sichuan province) [3], and the meagre biography of thor of “Springs and Autumns of the Ten Kingdoms”, Sun Guang-xian in Song dynastic history (j. 483) says Qing historian Wu Zhi-yi (吳志伊, second half of the same. Still, one of the most well-known works by 17th—first half of 18th century), says that it was at the him Bei meng suo yan (北夢瑣言, “Short Sayings from end of the rule of the Tang dynasty. -

Ceramic Tableware from China List of CNCA‐Certified Ceramicware
Ceramic Tableware from China June 15, 2018 List of CNCA‐Certified Ceramicware Factories, FDA Operational List No. 64 740 Firms Eligible for Consideration Under Terms of MOU Firm Name Address City Province Country Mail Code Previous Name XIAOMASHAN OF TAIHU MOUNTAINS, TONGZHA ANHUI HANSHAN MINSHENG PORCELAIN CO., LTD. TOWN HANSHAN COUNTY ANHUI CHINA 238153 ANHUI QINGHUAFANG FINE BONE PORCELAIN CO., LTD HANSHAN ECONOMIC DEVELOPMENT ZONE ANHUI CHINA 238100 HANSHAN CERAMIC CO., LTD., ANHUI PROVINCE NO.21, DONGXING STREET DONGGUAN TOWN HANSHAN COUNTY ANHUI CHINA 238151 WOYANG HUADU FINEPOTTERY CO., LTD FINEOPOTTERY INDUSTRIAL DISTRICT, SOUTH LIUQIAO, WOSHUANG RD WOYANG CITY ANHUI CHINA 233600 THE LISTED NAME OF THIS FACTORY HAS BEEN CHANGED FROM "SIU‐FUNG CERAMICS (CHONGQING SIU‐CERAMICS) CO., LTD." BASED ON NOTIFICATION FROM CNCA CHONGQING CHN&CHN CERAMICS CO., LTD. CHENJIAWAN, LIJIATUO, BANAN DISTRICT CHONGQING CHINA 400054 RECEIVED BY FDA ON FEBRUARY 8, 2002 CHONGQING KINGWAY CERAMICS CO., LTD. CHEN JIA WAN, LI JIA TUO, BANAN DISTRICT, CHONGQING CHINA 400054 BIDA CERAMICS CO.,LTD NO.69,CHENG TIAN SI GE DEHUA COUNTY FUJIAN CHINA 362500 NONE DATIAN COUNTY BAOFENG PORCELAIN PRODUCTS CO., LTD. YONGDE VILLAGE QITAO TOWN DATIAN COUNTY CHINA 366108 FUJIAN CHINA DATIAN YONGDA ART&CRAFT PRODUCTS CO., LTD. NO.156, XIANGSHAN ROAD, JUNXI TOWN, DATIAN COUNTY FUJIAN 366100 DEHUA KAIYUAN PORCELAIN INDUSTRY CO., LTD NO. 63, DONGHUAN ROAD DEHUA TOWN FUJIAN CHINA 362500 THE LISTED ADDRESS OF THIS FACTORY HAS BEEN CHANGED FROM "MAQIUYANG XUNZHONG XUNZHONG TOWN, DEHUA COUNTY" TO THE NEW EAST SIDE, THE SECOND PERIOD, SHIDUN PROJECT ADDRESS LISTED ABOVE BASED ON NOTIFICATION DEHUA HENGHAN ARTS CO., LTD AREA, XUNZHONG TOWN, DEHUA COUNTY FUJIAN CHINA 362500 FROM THE CNCA AUTHORITY IN SEPTEMBER 2014 DEHUA HONGSHENG CERAMICS CO., LTD. -

Migration, Identity, and Colonial Fantasies in a Fifth- Century Story Collection
The Journal of Asian Studies Vol. 80, No. 1 (February) 2021: 113–127. © The Association for Asian Studies, Inc. 2021 doi:10.1017/S0021911820003630 Migration, Identity, and Colonial Fantasies in a Fifth- Century Story Collection XIAOFEI TIAN Keywords: anomaly account (zhiguai), ethnicity, gender, identity, local cult, Man peoples, migration, settler colonialism, sexuality, social class T THE TURN OF the fifth century, a story about a man contesting real estate with a ghost Acirculated in several different versions in South China. In one of the versions, a young man discovered three lacquer coffins when digging a tomb for his deceased father and had the coffins reburied elsewhere. That night, he dreamed of Lu Su 魯肅 (172–217), the powerful minister in the southern Kingdom of Wu, who angrily announced that he would exact revenge. He also dreamed of his late father, who told him that Lu Su was fighting with him over the gravesite. Later, the young man found copious blood on his father’s seating mat.1 In the early fourth century, after the fall of the Jin capital Luoyang to the non-Han nomadic peoples, the royal house of the Jin dynasty and the great families of the north crossed the Yangzi River and established the Eastern Jin (317–420), with Jiankang 建 康 (modern Nanjing) as the new capital. In the story cited above, the deceased father, Wang Boyang 王伯陽, was likely a member of the aristocratic Wang clan from Langye (in modern Shandong), since his wife was none other than the niece of the famous min- ister Xi Jian 郗鑒 (269–339) of Gaoping (also in modern Shandong), as these northern aristocratic families maintained a strict code of intermarriage.2 The Langye Wang clan had settled not far from Jiankang, formerly the capital of the Kingdom of Wu. -

The Price of Orthodoxy: Issues of Legitimacy in the Later Liang and Later Tang*
臺大歷史學報第 35 期 BIBLID1012-8514(2005)35p.55-84 2 0 0 5 年6 月,頁 5 5 ~8 4 2005.5.16 收稿,2005.6.22 通過刊登 The Price of Orthodoxy: Issues of Legitimacy in the Later Liang and Later Tang* Fang, Cheng-hua** Abstract After the decline of the Tang imperial authority in the late ninth century, a number of local warlords competed to erect autonomous regimes by force, gradually establishing their own dynasties. The first two dynasties after the end of the Tang, the Later Liang and the Later Tang, grew out of the rival regimes established by Zhu Wen and Li Keyong. Both Zhu and Li were bellicose generals, but who increasingly came to realize the importance of legitimacy in the process of building their national regimes. To legitimize his power, Zhu Wen claimed that the Tang orthodox authority had been transmitted to him. In contrast, Li Keyong and his son legitimized their fight against Zhu by claiming that they carried the standard of Tang restoration. Although adopting different approaches, both two military-oriented regimes turned to civil issues, such as organizing the bureaucracy and performing rituals. From a cultural perspective, the political leaders’ interest in civil affairs preserved and promoted Confucian tradition under violent conditions. Their claims to orthodoxy before they effectively controlled all of China, however, retarded the military actions of these two regimes, because the attention of their rulers was diverted from the battlefield to civil affairs. This article will analyze the relationship between military expansion and the management of legitimation in both the Later Liang and the Later Tang. -

Congressional-Executive Commission on China
CONGRESSIONAL-EXECUTIVE COMMISSION ON CHINA ANNUAL REPORT 2015 ONE HUNDRED FOURTEENTH CONGRESS FIRST SESSION OCTOBER 8, 2015 Printed for the use of the Congressional-Executive Commission on China ( Available via the World Wide Web: http://www.cecc.gov U.S. GOVERNMENT PUBLISHING OFFICE 96–106 PDF WASHINGTON : 2015 For sale by the Superintendent of Documents, U.S. Government Publishing Office Internet: bookstore.gpo.gov Phone: toll free (866) 512–1800; DC area (202) 512–1800 Fax: (202) 512–2104 Mail: Stop IDCC, Washington, DC 20402–0001 VerDate Mar 15 2010 23:16 Oct 07, 2015 Jkt 000000 PO 00000 Frm 00003 Fmt 5011 Sfmt 5011 U:\DOCS\96106.TXT DEIDRE CONGRESSIONAL-EXECUTIVE COMMISSION ON CHINA LEGISLATIVE BRANCH COMMISSIONERS House Senate CHRISTOPHER H. SMITH, New Jersey, MARCO RUBIO, Florida, Cochairman Chairman JAMES LANKFORD, Oklahoma ROBERT PITTENGER, North Carolina TOM COTTON, Arkansas TRENT FRANKS, Arizona STEVE DAINES, Montana RANDY HULTGREN, Illinois BEN SASSE, Nebraska TIMOTHY J. WALZ, Minnesota SHERROD BROWN, Ohio MARCY KAPTUR, Ohio DIANNE FEINSTEIN, California MICHAEL M. HONDA, California JEFF MERKLEY, Oregon TED LIEU, California GARY PETERS, Michigan EXECUTIVE BRANCH COMMISSIONERS CHRISTOPHER P. LU, Department of Labor SARAH SEWALL, Department of State STEFAN M. SELIG, Department of Commerce DANIEL R. RUSSEL, Department of State TOM MALINOWSKI, Department of State PAUL B. PROTIC, Staff Director ELYSE B. ANDERSON, Deputy Staff Director (II) VerDate Mar 15 2010 23:16 Oct 07, 2015 Jkt 000000 PO 00000 Frm 00004 Fmt 0486 Sfmt 0486 U:\DOCS\96106.TXT DEIDRE CO N T E N T S Page I. Executive Summary ............................................................................................. 1 Overview ............................................................................................................ 2 Key Recommendations ....................................................................................