DOCSLIB.ORG

The Yield Curve.  Indeed, the Yield Curve Is Probably the Only True Market Indicator and Potential Forecaster of the Market

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Yield Curve.  Indeed, the Yield Curve Is Probably the Only True Market Indicator and Potential Forecaster of the Market Bond Basics By A.V. Vedpuriswar Bond basics A bond is an IOU between the Issuer and the investors. In most cases, the loan is for a fixed term, so that there is a specified repayment date. There is also (in most cases) a fixed interest rate or coupon. In other words, a bond is a package of cash flows, which are received by the bondholder at future dates until repayment. The price of a package of future cash flows is its “net present value”. This value will fluctuate with changes in market interest rates. Therefore, during its life the price of the bond will fluctuate, and will move towards 100 (“par”) on maturity date. Basic definitions Yield The interest rate which can be earned on an investment, currently quoted by the market or implied by the current market price for the investment. Not to be confused with the coupon paid by an issuer on a security, which is the coupon rate multiplied by the face value. For a bond, it is the yield to maturity unless otherwise specified. Yield to maturity The internal rate of return of a bond The yield necessary to discount all the bond’s cash flows to an NPV equal to its current price. It equals all the interest payments received (and assumes that we will reinvest the interest payment at the same rate as the current yield on the bond) plus any gain (if we purchased at a discount) or loss (if we purchased at a premium). Yield to equivalent life The same as yield to maturity for a bond with partial redemptions. The Yield Curve The bond market’s main prediction tool is the yield curve. Indeed, the yield curve is probably the only true market indicator and potential forecaster of the market. The shape of the yield curve has correctly predicted every recession in the US since the war. The yield curve plots the yield on a group of bonds against their maturities. Only the same class of bonds can be plotted together (gilts, Treasuries, AA Sterling Eurobonds, etc) The conventional shape of the curve is gently upward sloping . The curve can be inverted if market is expecting recession or for specific structural factors . In the United States, the Treasury yield curve is the first mover of all domestic interest rates and an influential factor in setting global rates. Interest rates on all other domestic bond categories rise and fall with Treasuries which are the debt securities issued by the U.S. government. To attract investors, any bond or debt security that contains greater risk than that of a similar Treasury bond must offer a higher yield. For example, the 30-year mortgage rate historically runs 1% to 2% above the yield on 30-year Treasury bonds. Normal yield curve The longer the maturity the higher the yield expected by investors Historical yield trends in the US 10 1 Spread Factors affecting yields Factors affecting yields Useful definitions Par yield curve A curve plotting maturity against yield for bonds priced at par. Asset & Liability Management (ALM) The practice of matching the maturity and cash flows of an organisation’s asset and liability portfolios to maximise returns and minimise risk. Also includes the deliberate mis-matching of cash flows to take account of views on the short-term yield curve. Benchmark A bond whose terms set a standard for the market. The benchmark usually has the greatest liquidity. It also usually trades expensive relative to the yield curve, due to higher demand for it amongst institutional investors. More definitions(Contd) Convexity A measure of the curvature of a bond’s price/yield curve (mathematically). Yield-curve option Option that allows purchasers to take a view on a yield curve without having to take a view about a market’s direction. Yield-curve swap Swap in which the index rates of the two interest streams are at different points on the yield curve. Both payments are refixed with the same frequency whatever the index rate. Zero-coupon A zero-coupon security is one that does not pay a coupon. Its price is correspondingly less to compensate for this. A zero-coupon yield is the yield which a zero-coupon investment for that term would have if it were consistent with the par yield curve. Z-spread The z-spread is a spread of a bond yield to a yield curve. It is the basis point spread that would need to be added to the implied spot yield curve such that the discounted cash flows of a bond are equal to its present value (its current market price). Each bond cash flow would be discounted by the relevant spot rate for its maturity term. This differs from a conventional swap spread which has been calculated using the bond's yield-to-maturity to discount all its cash flows. Both spreads can be viewed as the coupon of a swap market annuity of equivalent credit risk of the bond being valued. Bond price fluctuations A bond's price changes on a daily basis, just like that of any other publicly traded security. Many investors do not hold bonds to maturity. At any time, a bond can be sold in the open market, where the price can fluctuate, sometimes dramatically. Simple Yield calculations Yield is a figure that shows the return we get on a bond. The simplest version of yield is calculated using the following formula: Yield = coupon amount/price. When we buy a bond at par, yield is equal to the interest rate. When the price changes, so does the yield. If we buy a bond with a 10% coupon at its $1,000 par value, the yield is 10% ($100/$1,000). But if the price goes down to $800, then the yield goes up to 12.5%. Conversely, if the bond goes up in price to $1,200, the yield shrinks to 8.33% ($100/$1,200). Understanding the Link Between Price and Yield When interest rates rise, the prices of bonds in the market fall. Thereby raising the yield of the older bonds And bringing them into line with newer bonds being issued with higher coupons. When interest rates fall, the prices of bonds in the market rise. Thereby lowering the yield of the older bonds. And bringing them into line with newer bonds being issued with lower coupons. If we are a bond buyer, we want high yields. On the other hand, if we already own a bond, we have locked in our interest rate, so we hope the price of the bond goes up. This way we can cash out by selling our bond in the future. Illustration A zero coupon bond of redemption value $1,000,000 is trading at $ 950,000 1 year ahead of maturity. What is the yield? Solution Price = $ 950,000 Interest = $ 50,000 Yield = $ 50,000/$950,000 = 1/19 = .0526 GEN0190n.ppt 16 = 5.26% Illustration What is the yield to maturity of a bond of face value $ 1000, redemption period of 3 years, coupon = 4% and the bond is being traded at $ 950? GEN0190n.ppt 17 40 40 1040 950 (1 r) (1 r)2 (1 r)3 r .06 Illustration Three month, $ 1 million Eurodollar futures are trading at 89.25. A speculator believes interest rates are going to rise. What should he do ? If on the date of settlement, futures quote 88.75, what is his gain or loss? Solution Futures price = 100- yield Sell futures 100-89.25 = (1,000,000- A)/(1,000,000)x400 A = $ 973,125 100-88.75= (1,000,000-B)/(1,000,000)x400 B = $ 971,875 Gain = A - B = 973,125 - 971,875 = 1250 Illustration On January 5, March futures maturing after 77 days on March 22 are yielding 12.50%. 167 day T Bills are now yielding 10% while 77 day T Bills are yielding 6%. The yields given are actual and based on daily compounding. Are there any arbitrage possibilities ? Borrow for 77 days, Invest for 167 days, Sell March futures After 77 days, collect money realised against sale of futures Give delivery of T Bill and repay loan. Price of 167 day T Bill = (1,000,000)/(1+.10)167/360 = $ 956,750 Borrow $ 956,750 for 77 days. After 77 days, realisation from sale of futures = (1,000,000)/(1+.125)90/360 = $ 970,984 Repayment of loan = (956,750)(1+.06)77/360 = $ 968,749 Profit = 970,984 - 968,749 = $ 2235 Illustration Repeat previous problem if yield on 77 day T Bills is 8%. Buy March futures. Borrow for 167 days. Invest for 77 days In March, collect money from maturing 77 day T Bill. Pay and take delivery against March futures. Hold till delivery. To buy future we need 1,000,000/(1+.125)90/360 = $ 970,984 Investment today = 970,984/(1+0.08)77/360 = $ 955,131 Issue 167 day T Bill for $ 955,131 Buy 77 day T Bill for $ 955,131 Outflow after 167 days = (955,131)(1+.10)167/360= 988,308 Gain = 1,000,000 - 998,308 = $1,692 Government Bonds In general, fixed-income securities are classified according to the length of time before maturity. These are the three main categories: Bills - debt securities maturing in less than one year. Notes - debt securities maturing in one to 10 years. Bonds - debt securities maturing in more than 10 years. Marketable securities from the U.S. government - known collectively as Treasuries - follow this guideline and are issued as Treasury bonds, Treasury notes and Treasury bills (T-bills).
Load more

Recommended publications
  • 3. VALUATION of BONDS and STOCK Investors Corporation
    3. VALUATION OF BONDS AND STOCK Objectives: After reading this chapter, you should be able to: 1. Understand the role of stocks and bonds in the financial markets. 2. Calculate value of a bond and a share of stock using proper formulas. 3.1 Acquisition of Capital Corporations, big and small, need capital to do their business. The investors provide the capital to a corporation. A company may need a new factory to manufacture its products, or an airline a few more planes to expand into new territory. The firm acquires the money needed to build the factory or to buy the new planes from investors. The investors, of course, want a return on their investment. Therefore, we may visualize the relationship between the corporation and the investors as follows: Capital Investors Corporation Return on investment Fig. 3.1: The relationship between the investors and a corporation. Capital comes in two forms: debt capital and equity capital. To raise debt capital the companies sell bonds to the public, and to raise equity capital the corporation sells the stock of the company. Both stock and bonds are financial instruments and they have a certain intrinsic value. Instead of selling directly to the public, a corporation usually sells its stock and bonds through an intermediary. An investment bank acts as an agent between the corporation and the public. Also known as underwriters, they raise the capital for a firm and charge a fee for their services. The underwriters may sell $100 million worth of bonds to the public, but deliver only $95 million to the issuing corporation.
    [Show full text]
  • The Use of Credit Default Swaps by U.S. Fixed-Income Mutual Funds
    Sanjiv R. Das FDIC Center for Financial Research Darrell Duffie Working Paper Nikunj Kapadia No. 2011-01 Empirical Comparisons and Implied Recovery Rates The Use of Credit Default Swaps by U.S Fixed-Income Mutual Funds Risk-Based Capital Standards, kkk Deposit Insurance and Procyclicality November 19, 2010 Risk-Based Capital Standards, Deposit Insurance and Procyclicality An Empirical September 2005 An Empirical Analysis Federal Dposit Insurance Corporation •Center for Financial Researchh State- May, 2005 Efraim Benmel Efraim Benmelech June 20 May , 2005 Asset S2005-14 The Use of Credit Default Swaps by U.S. Fixed-Income Mutual Funds Tim Adam, Humboldt University* and Risk Management Institute (Singapore) Andre Guettler, University of Texas at Austin and EBS Business School† November 19, 2010 Abstract We examine the use of credit default swaps (CDS) in the U.S. mutual fund industry. We find that among the largest 100 corporate bond funds the use of CDS has increased from 20% in 2004 to 60% in 2008. Among CDS users, the average size of CDS positions (measured by their notional values) increased from 2% to almost 14% of a fund’s net asset value. Some funds exceed this level by a wide margin. CDS are predominantly used to increase a fund’s exposure to credit risks rather than to hedge credit risk. Consistent with fund tournaments, underperforming funds use multi-name CDS to increase their credit risk exposures. Finally, funds that use CDS underperform funds that do not use CDS. Part of this underperformance is caused by poor market timing. JEL-Classification: G11, G15, G23 Keywords: Corporate bond fund, credit default swap, credit risk, fund performance, hedging, speculation, tournaments * Humboldt University, Institute of Corporate Finance, Dorotheenstr.
    [Show full text]
  • Connecticut Ladder 1 to 5 Year Municipal Fixed Income Sample Portfolio August 9, 2021
    Connecticut Ladder 1 to 5 Year Municipal Fixed Income Sample Portfolio August 9, 2021 % of Sample Bonds Sample Portfolio Characteristics S&P Rating ^ Portfolio Sample Portfolio Sector Allocation (Bonds Only) Only (Bonds Only) LD1-5CTNETAVERAGE ASSETS EFFECTIVE DURATION (YRS) 2.62 AAA 40.3% LD1-5CTNETAVERAGE ASSETS MATURITY/LIFE (YRS) 2.82 AA 49.6% LD1-5CTNETAVERAGE ASSETS COUPON (%) 4.81 A 10.1% LD1-5CTNETAVERAGE ASSETS CURRENT YIELD(%) 4.29 BBB 0.0% LD1-5CTNETAVERAGE ASSETS YIELD TO WORST(%) 0.24 NR 0.0% LD1-5CTNETAVERAGE ASSETS YIELD TO MATURITY(%) 0.24 AVERAGE TAX EQUIVALENT YIELD TO WORST (%) 0.40 AVERAGE TAX EQUIVALENT YIELD TO MATURITY (%) 0.40 Revenue 40% General Sample Portfolio Representation Bond Holdings Obligation Yield to 60% Effective Moody's S&P Description Coupon (%) Maturity Price ($) Worst Duration Rating Rating 0 (%) 1LD1-5CTMunicipalsTEXAS TRANSN COMMN ST HWY FD R 5.000 04/01/22 103.15 0.63 years 0.08 Aaa AAA 2LD1-5CTMunicipalsNORTH CAROLINA ST LTD OBLIG 5.000 06/01/22 103.98 0.80 years 0.07 Aa1 AA+ 3LD1-5CTMunicipalsUNIVERSITY CONN 5.000 02/15/23 107.28 1.45 years 0.19 Aa3 A+ 4LD1-5CTMunicipalsMASSACHUSETTS ST TRANSN FD REV 5.000 06/01/23 108.86 1.74 years 0.10 Aa1 AA+ 5LD1-5CTMunicipalsCHANDLER ARIZ 5.000 07/01/24 114.04 2.73 years 0.14 Aaa AAA 6LD1-5CTMunicipalsWEST HARTFORD CONN 5.000 10/01/24 115.13 2.92 years 0.17 NR AAA 7LD1-5CTMunicipalsBLOOMFIELD CONN 5.000 01/15/25 116.03 3.21years 0.30 NR AA+ 8LD1-5CTMunicipalsNEW YORK N Y 4.000 08/01/25 114.49 3.73 years 0.33 Aa2 AA Sample Portfolio Duration Distribution (Bonds Only) 9LD1-5CTMunicipalsBROOKFIELD CONN 4.000 08/15/26 117.48 4.48 years 0.47 NR AAA 10LD1-5CTMunicipalsENFIELD CT 5.000 08/01/26 121.99 4.52 years 0.52 NR AA 11LD1-5CTMunicipals 12LD1-5CTMunicipals 100% 13LD1-5CTMunicipals 90% 14LD1-5CTMunicipals 15LD1-5CTMunicipals 80% 16LD1-5CTMunicipals 70% 17LD1-5CTMunicipals 18LD1-5CTMunicipals 60% 19LD1-5CTMunicipals 50% 20LD1-5CTMunicipals 39.79% 40.45% 40% 30% 19.75% 20% 10% 0.00% 0% 0-2 2-4 4-6 >6 Years MASH0421U/S-1585094-1/2 Source: BlackRock, Bloomberg, Reuters.
    [Show full text]
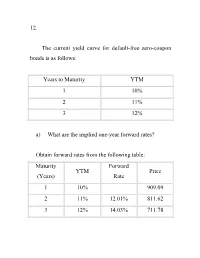
  • 12. the Current Yield Curve for Default-Free Zero-Coupon Bonds Is
    12. The current yield curve for default-free zero-coupon bonds is as follows: Years to Maturity YTM 1 10% 2 11% 3 12% a) What are the implied one-year forward rates? Obtain forward rates from the following table: Maturity Forward YTM Price (Years) Rate 1 10% 909.09 2 11% 12.01% 811.62 3 12% 14.03% 711.78 b) Assume the pure expectations hypothesis is correct. If market expectations are correct, what will the yield curve on one- and two-year zero-coupon bonds be next year? Maturity (Years) Price YTM 1 1000/1.1201 12.01% 2 1000/[1.1201*1.1403] 13.02% c) If you purchase a two-year zero-coupon bond now, what is the expected total rate of return over the next year? What if you purchase a three-year zero- coupon bond? Next year, the 2-year zero will be a 1 year zero, and will sell at 892.78; likewise, the 3-year zero will be a 2-year zero trading at 782.93. Expected total rate of return: 2-Year: (892.78/811.62) – 1 = 10% 3-Year: (782.93/711.78) – 1 = 10% d) What should be the current price of a three-year maturity bond with a 12% coupon rate paid annually? If you purchased it at that price, what would your total expected rate of return be over the next year? The current price of the bond should equal the value of each payment times the present value of $1 to be received at the maturity of that payment.
    [Show full text]
  • Chapter 10 Bond Prices and Yields Questions and Problems
    CHAPTER 10 Bond Prices and Yields Interest rates go up and bond prices go down. But which bonds go up the most and which go up the least? Interest rates go down and bond prices go up. But which bonds go down the most and which go down the least? For bond portfolio managers, these are very important questions about interest rate risk. An understanding of interest rate risk rests on an understanding of the relationship between bond prices and yields In the preceding chapter on interest rates, we introduced the subject of bond yields. As we promised there, we now return to this subject and discuss bond prices and yields in some detail. We first describe how bond yields are determined and how they are interpreted. We then go on to examine what happens to bond prices as yields change. Finally, once we have a good understanding of the relation between bond prices and yields, we examine some of the fundamental tools of bond risk analysis used by fixed-income portfolio managers. 10.1 Bond Basics A bond essentially is a security that offers the investor a series of fixed interest payments during its life, along with a fixed payment of principal when it matures. So long as the bond issuer does not default, the schedule of payments does not change. When originally issued, bonds normally have maturities ranging from 2 years to 30 years, but bonds with maturities of 50 or 100 years also exist. Bonds issued with maturities of less than 10 years are usually called notes.
    [Show full text]
  • Glossary of Bond Terms
    Glossary of Bond Terms Accreted value- The current value of your zero-coupon municipal bond, taking into account interest that has been accumulating and automatically reinvested in the bond. Accrual bond- Often the last tranche in a CMO, the accrual bond or Z-tranche receives no cash payments for an extended period of time until the previous tranches are retired. While the other tranches are outstanding, the Z-tranche receives credit for periodic interest payments that increase its face value but are not paid out. When the other tranches are retired, the Z-tranche begins to receive cash payments that include both principal and continuing interest. Accrued interest- (1) The dollar amount of interest accrued on an issue, based on the stated interest rate on that issue, from its date to the date of delivery to the original purchaser. This is usually paid by the original purchaser to the issuer as part of the purchase price of the issue; (2) Interest deemed to be earned on a security but not yet paid to the investor. Active tranche- A CMO tranche that is currently paying principal payments to investors. Adjustable-rate mortgage (ARM)- A mortgage loan on which interest rates are adjusted at regular intervals according to predetermined criteria. An ARM's interest rate is tied to an objective, published interest rate index. Amortization- Liquidation of a debt through installment payments. Arbitrage- In the municipal market, the difference in interest earned on funds borrowed at a lower tax-exempt rate and interest on funds that are invested at a higher-yielding taxable rate.
    [Show full text]
  • Corporate Bonds
    investor’s guide CORPORATE BONDS i CONTENTS What are Corporate Bonds? 1 Basic Bond Terms 2 Types of Corporate Bonds 5 Bond Market Characteristics 7 Understanding the Risks 8 Understanding Collateralization and Defaults 13 How Corporate Bonds are Taxed 15 Credit Analysis and Other Important Considerations 17 Glossary 21 All information and opinions contained in this publication were produced by the Securities Industry and Financial Markets Association (SIFMA) from our membership and other sources believed by SIFMA to be accurate and reli- able. By providing this general information, SIFMA is neither recommending investing in securities, nor providing investment advice for any investor. Due to rapidly changing market conditions and the complexity of investment deci- sions, please consult your investment advisor regarding investment decisions. ii W H A T A R E C O R P O R A T E BONDS? Corporate bonds (also called “corporates”) are debt obligations, or IOUs, issued by privately- and publicly-owned corporations. When you buy a corpo- rate bond, you essentially lend money to the entity that issued it. In return for the loan of your funds, the issuer agrees to pay you interest and to return the original loan amount – the face value or principal - when the bond matures or is called (the “matu- rity date” or “call date”). Unlike stocks, corporate bonds do not convey an ownership interest in the issuing corporation. Companies use the funds they raise from selling bonds for a variety of purposes, from building facilities to purchasing equipment to expanding their business. Investors buy corporates for a variety of reasons: • Attractive yields.
    [Show full text]
  • Current Income Portfolio Holdings
    Current Income Portfolio Holdings YTM1 CURRENT % OF CURRENT YIELD % OF SECTOR/SECURITY MATURITY RATING SECTOR/SECURITY MATURITY RATING (%) YIELD (%) PORTFOLIO (%) PORTFOLIO CORPORATES 74.66 PREFERRED SECURITIES 24.12 MOTOROLA SOLUTIONS INC 05/23/2029 Baa3 2.75 4.05 4.61 NEXTERA ENERGY CAPITAL 03/01/2079 Baa2 5.04 2.24 FISERV INC 10/01/2028 Baa2 2.35 3.73 4.51 DUKE ENERGY CORP 09/15/2078 Baa3 5.24 2.15 CITIGROUP INC 07/25/2028 Baa2 2.56 3.74 4.45 AT&T INC 08/01/2067 Baa2 5.36 2.10 HP INC 06/17/2027 Baa2 2.00 2.83 4.27 AMERICAN INTL GROUP PERP Baa3 5.31 2.21 DISCOVER FINANCIAL SVS 02/09/2027 Baa3 2.08 3.69 4.47 ALLSTATE CORP PERP Baa2 4.72 2.16 GOLDMAN SACHS GROUP INC 02/25/2026 A2 1.67 3.42 4.41 BANK OF AMERICA CORP PERP Baa3 4.96 2.17 BOSTON PROPERTIES LP 02/01/2026 Baa1 1.66 3.34 4.40 JPMORGAN CHASE & CO PERP Baa2 5.46 2.20 COMCAST CORP 08/15/2025 A3 1.26 3.10 4.38 PNC FINANCIAL SERVICES PERP Baa2 5.74 2.14 MORGAN STANLEY 07/23/2025 A1 1.37 3.60 4.48 PUBLIC STORAGE PERP A3 5.02 2.24 CAPITAL ONE FINANCIAL CO 02/05/2025 Baa1 1.38 3.00 4.30 STATE STREET CORP PERP Baa1 4.64 2.31 BECTON DICKINSON AND CO 12/15/2024 Baa3 1.18 3.42 4.42 US BANCORP PERP A3 5.01 2.20 WALGREENS BOOTS 11/18/2024 Baa2 1.29 3.49 4.42 CASH 1.20 ALLIANCE TOTAL PORTFOLIO 100.00 VERIZON COMMUNICATIONS 11/01/2024 Baa1 1.07 3.23 4.41 ANTHEM INC 08/15/2024 Baa2 1.05 3.24 4.35 MCKESSON CORP 03/15/2024 Baa2 0.87 3.50 4.35 2 2 PORTFOLIO STATISTICS PORTFOLIO BENCHMARK WILLIAMS COMPANIES INC 01/15/2023 Baa3 1.08 3.54 4.22 TYSON FOODS INC 06/15/2022 Baa2 1.28 4.33 4.21 Current Yield (%) 3.84 2.06 Credit Rating (Moody’s) Baa1 Aa2 Yield-To-Maturity(%) 2.38 1.00 Option-Adjusted (Effective) Duration 4.03 4.09 1 Yield-to-maturity.
    [Show full text]
  • 1 Overview of Derivatives
    1 Overview of Derivatives A financial derivative is usually defined as an instrument whose value is derived from some underlying cash market instrument. Familiar examples include • options to { buy (\call options") or { sell (\put options") a specified security or commodity at a specified price on a specified date, and • contracts such as { futures or { options on equity indices such Standard & Poor's 500. Newer examples include structured notes, which are securities whose interest or principal payments depend on market conditions, such as floating rate notes and inverse floaters. Swaps of various kinds are also derivatives. Various kinds of derivative are described by Hull, with both details of how their markets operate and the theory of pricing. 1.1 Exchange-Traded versus Over-the-Counter A significant distinction is that between exchange-traded and over-the-counter (\OTC") derivatives. Derivatives that are traded on an exchange are stan- dardized to promote liquidity. They are \marked to market" as of the close of business every day, and the holder's brokerage account is credited or deb- ited with the day's change in value. The holder is required to keep cash or securities in the account sufficient to cover the next day's possible losses with a very high level of probability; this margin protects the other partici- pants against default by the holder of an \out of the money" position. Each instrument is a contract between the holder and the exchange. The OTC market consists of an informal system of dealers linked by telephone, and allows transactions to be customized to meet the precise needs 1 of the dealers' clients.
    [Show full text]
  • Current Yield Calculation
    Current Yield Calculation Current yield is the annual rate of return that an investor purchasing a security at its market price would realize. Generally speaking, it is the annual income from a security divided by the current price of the security, expressed as a percentage. However, the calculation for annual income can vary, depending on the security type and settings for the security. This document explains the various calculations and settings and how they affect the Current Yield you see on portfolio holdings reports in PortfolioCenter. Calculations for Current Yield Because current values can be calculated differently for different security types, the current yield calculation can also vary by security type. This document covers three main categories of security types: Equities, Mutual Funds, Unit Trusts – see the calculation information starting on page 2 Fixed Income, CDs and Mortgage-Backed Securities – see the calculation information starting on page 5. Other Security Types – see information about other security types starting on page 6. Each section shows the calculation for that category, followed by examples of the calculation. DocumentID: SPT010870 Last Updated: January 20, 2011 Equities, Mutual Funds, Unit Trusts and User Defined Securities The calculation for Current Yield for equities, mutual funds, unit trusts and user defined securities is: The Annual Income per Share calculation, or the numerator of the formula above, depends on the status of the Allow Updates checkbox in the security details for each security. Allow Updates is checked in Security Details: One way to calculate current yield is to check the Allow Updates box on the General tab of the security details, similar to the example on the right.
    [Show full text]
  • Active Fixed Income: a Primer
    Active Fixed Income: A Primer ©Madison Investment Advisors, LLC. September 2016. madisonadv.com Active Fixed Income: A Primer Most investors have a basic understanding of equity securities and may even spend a good deal of leisure time reading about stocks and watching equity-focused news shows. Mention bonds and you often get a glazed look. When it comes to fixed income strategy, some investors are familiar with the simplest approach: buying bonds and holding until maturity. Using this strategy, the investor’s return is approximately the average yield of the bonds in the portfolio. However, few have an appreciation of the techniques and potential advantages of active management. This primer looks at active fixed income management and the methods used in the effort to add value. There are two basic ways to add value: generate a total return above what a buy and hold (or yield only) strategy would generate; or reduce volatility from a fixed income portfolio so that more risk can be taken elsewhere in pursuit of greater overall portfolio rewards. Table of Contents Active Bond Management Overview .............................................................. 1 Duration Management ..................................................................................... 3 Active Yield Curve Management .................................................................... 6 Sector and Spread Management .................................................................... 9 Credit Risk Management ..............................................................................
    [Show full text]
  • Fabozzi Course.Pdf
    Asset Valuation Debt Investments: Analysis and Valuation Joel M. Shulman, Ph.D, CFA Study Session # 15 – Level I CFA CANDIDATE READINGS: Fixed Income Analysis for the Chartered Financial Analyst Program: Level I and II Readings, Frank J. Fabozzi (Frank J. Fabozzi Associates, 2000) “Introduction to the Valuation of Fixed Income Securities,” Ch. 5 “Yield Measures, Spot Rates, and Forward Rates,” Ch. 6 “Introduction to Measurement of Interest Rate Risk,” Ch. 7 © 2002 Shulman Review/The Princeton Review Fixed Income Valuation 2 Learning Outcome Statements Introduction to the Valuation of Fixed Income Securities Chapter 5, Fabozzi The candidate should be able to a) Describe the fundamental principles of bond valuation; b) Explain the three steps in the valuation process; c) Explain what is meant by a bond’s cash flow; d) Discuss the difficulties of estimating the expected cash flows for some types of bonds and identify the bonds for which estimating the expected cash flows is difficult; e) Compute the value of a bond, given the expected cash flows and the appropriate discount rates; f) Explain how the value of a bond changes if the discount rate increases or decreases and compute the change in value that is attributable to the rate change; g) Explain how the price of a bond changes as the bond approaches its maturity date and compute the change in value that is attributable to the passage of time; h) Compute the value of a zero-coupon bond; i) Compute the dirty price of a bond, accrued interest, and clean price of a bond that is between coupon
    [Show full text]