Security Analysis: an Investment Perspective
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Synergies of Hedge Funds and Reinsurance
The Synergies of Hedge Funds and Reinsurance Eric Andersen May 13th, 2013 Advisor: Dwight Jaffee Department of Economics University of California, Berkeley Acknowledgements I would like to convey my sincerest gratitude to Dr. Dwight Jaffee, my advisor, whose support and assistance were crucial to this project’s development and execution. I also want to thank Angus Hildreth for providing critical feedback and insightful input on my statistical methods and analyses. Credit goes to my Deutsche Bank colleagues for introducing me to and stoking my curiosity in a truly fascinating, but infrequently studied, field. Lastly, I am thankful to the UC Berkeley Department of Economics for providing me the opportunity to engage this project. i Abstract Bermuda-based alternative asset focused reinsurance has grown in popularity over the last decade as a joint venture for hedge funds and insurers to pursue superior returns coupled with insignificant increases in systematic risk. Seeking to provide permanent capital to hedge funds and superlative investment returns to insurers, alternative asset focused reinsurers claim to outpace traditional reinsurers by providing exceptional yields with little to no correlation risk. Data examining stock price and asset returns of 33 reinsurers from 2000 through 2012 lends little credence to support such claims. Rather, analyses show that, despite a positive relationship between firms’ gross returns and alternative asset management domiciled in Bermuda, exposure to alternative investments not only fails to mitigate market risk, but also may actually eliminate any exceptional returns asset managers would have otherwise produced by maintaining a traditional investment strategy. ii Table of Contents Acknowledgements .......................................................................................................................... i Abstract .......................................................................................................................................... -

29:390:470:01 & 02 COURSE TITLE: Security Analysis
Department of Finance and Economics COURSE NUMBER: 29:390:470:01 & 02 COURSE TITLE: Security Analysis COURSE MATERIALS Lecture notes and assignments will be distributed via Blackboard. Required Textbooks: 1) “Value Investing – from Graham to Buffett and Beyond”, Bruce Greenwald, Judd Kahn, Paul Sonkin and Michael Biema. Wiley Finance. ISBN 0-471-46339-6 2) “The Warren Buffett Way”, 3rd Edition, Robert Hagstrom, Wiley Other readings (buy used copies): 3) “The Intelligent Investor”, Benjamin Graham. Revised Edition 2006 by Harper Collins Publishers. ISBN-10 0-06-055566-1 4) “Security Analysis”, 1951 Edition”, Benjamin Graham & David L. Dodd by McGraw Hill. ISBN 0-07-144820-9 5) “The Essays of Warren Buffett: Lessons for Corporate America”, First Revised Edition, by Lawrence A. Cunningham, ISBN-10: 0-9664461-1-9 6) “Investment Banking: Valuation, Leveraged Buyouts, and Mergers and Acquisitions”, Joshua Rosenbaum, Joshua Pearl and Joseph R. Perella (Wiley Finance) 2009. ISBN 978-0-470-44220-3 FINAL GRADE ASSIGMENT Grades Mid-Term: 40% Equity Challenge competition: 60% (team work) Teams: Each student must be part of a team of 4 members. Please take advantage of student diversity in your class. Your team is expected to work on class assignments and the equity challenge competition. 1 Department of Finance and Economics (29:390:470) COURSE SCHEDULE Course Outline Week 1: Principles of Security Analysis Lectures 1A & 1B Buying a business Lecture 1C Read Accounting Clinic 1 Appendix 1 Week 2: Balance Sheet, Income Statement Lectures 2A & 2B Appendix -

The Association of Exchange Rates and Stock Returns. (Linear Regression Analysis)
March 2007 U.S.B.E- Umeå School of Business Masters Program: Accounting and Finance Masters Thesis- Spring Semester 2007 Author : Akumbu Martin Nshom Supervisor : Stefan Sundgren Thesis seminar : 7 th May 2007 The Association of Exchange rates and Stock returns. (Linear regression Analysis) Acknowledgement I will start by thanking God Almighty for giving me the intellect to complete this project. A big thanks goes to my supervisor Stefan Sundgren for giving me guidance and all the help I needed to complete this thesis To my family for their continuous help and support to see that I under take my studies here especially my Mother Lydia Botame. Finally to all my friends and well wishers who supported me in one way or an other through out my stay here in Umeå, may God bless you all! ABSTRACT The association of exchange rates with stock returns and performance in major trading markets is widely accepted. The world’s economy has seen unprecedented growth of interdependent; as such the magnitude of the effect of exchange rates on returns will be even stronger. Since the author perceives the importance of exchange rates on stock returns, the author found it interesting to study the effect of exchange rates on some stocks traded on the Stock exchange. There has been a renewed interest to investigate the relationship between returns and exchange rates as such; the author has chosen to investigate the present study to focus in the United Kingdom with data from the London Stock exchange .The author carried out his research on 18 companies traded on the London Stock Exchange in the process, using linear regression analysis. -
Unit 1: Investments
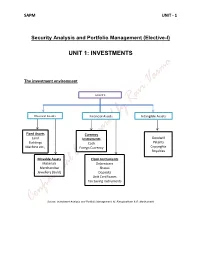
SAPM UNIT - 1 Security Analysis and Portfolio Management (Elective-I) UNIT 1: INVESTMENTS The investment environment ASSETS Physical Assets Financial Assets Intangible Assets Fixed Assets Currency Goodwill Land Instruments Patents Buildings Cash Machine etc., Copyrights Foregn Currency Royalties Movable Assets Claim Instruments Materials Debentures Merchandise Shares Jewellery (Gold) Deposits Unit Certificates Tax Saving Instruments Source: Investment Analysis and Portfolio Management, M. Ranganatham & R. Madhumathi SAPM UNIT - 1 Classification of Financial Markets: Financial Markets Securities Market Currency Market/ Forex market National Market International Market Domestic Segment Foreign Segment Capital Market Money Market Equity Market Debt Market Primary Market Secondary Market Spot Market Derivative Market Source: Investment Analysis and Portfolio Management, M. Ranganatham & R. Madhumathi SAPM UNIT - 1 SAPM UNIT - 1 Investment Meaning & Definition: investment is an activity that is engaged in by people who have savings i.e. investments are made from savings. Investment may be defined as a “commitment of funds made in the expectations of some positive rate of return.” Characteristics of Investment: Return Risk Safety Liquidity Objectives of Investment: Maximisation of Return Minimization of Risk Hedge against Inflation Investment Vs Speculation: Traditionally investment is distinguished from speculation with respect to four factors. These are: Risk Capital Gain Time Period Leverage Financial instruments (Investment Avenues available in India): Corporate Securities Deposits in banks and non-banking companies UTI and other mutual fund schemes SAPM UNIT - 1 Post office deposits and certificates Life insurance policies Provident fund schemes Government and semi government securities Regulatory Environment: In India the ministry of finance, the reserve bank of india, the securities and exchange board of India etc. -

Ba7021 Security Analysis and Portfolio Management 1 Sce
BA7021 SECURITY ANALYSIS AND PORTFOLIO MANAGEMENT A Course Material on SECURITY ANALYSIS AND PORTFOLIO MANAGEMENT By Mrs.V.THANGAMANI ASSISTANT PROFESSOR DEPARTMENT OF MANAGEMENT SCIENCES SASURIE COLLEGE OF ENGINEERING VIJAYAMANGALAM 638 056 1 SCE DEPARTMENT OF MANAGEMENT SCIENCES BA7021 SECURITY ANALYSIS AND PORTFOLIO MANAGEMENT QUALITY CERTIFICATE This is to certify that the e-course material Subject Code : BA7021 Subject : Security Analysis and Portfolio Management Class : II Year MBA Being prepared by me and it meets the knowledge requirement of the university curriculum. Signature of the Author Name : V.THANGAMANI Designation: Assistant Professor This is to certify that the course material being prepared by Mrs.V.THANGAMANI is of adequate quality. He has referred more than five books amount them minimum one is from abroad author. Signature of HD Name: S.Arun Kumar SEAL 2 SCE DEPARTMENT OF MANAGEMENT SCIENCES BA7021 SECURITY ANALYSIS AND PORTFOLIO MANAGEMENT CONTENTS CHAPTER TOPICS PAGE NO INVESTMENT SETTING 1.1 Financial meaning of investment 1.2 Economic meaning of Investment 7-25 1 1.3 Characteristics and objectives of Investment 1.4 Types of Investment 1.5 Investment alternatives 1.6 Choice and Evaluation 1.7 Risk and return concepts. SECURITIES MARKETS 2.1 Financial Market 2.2 Types of financial markets 2.3 Participants in financial Market 2.4 Regulatory Environment 2 2.5 Methods of floating new issues, 26-64 2.6 Book building 2.7 Role & Regulation of primary market 2.8 Stock exchanges in India BSE, OTCEI , NSE, ISE 2.9 Regulations of stock exchanges 2.10 Trading system in stock exchanges 2.11 SEBI FUNDAMENTAL ANALYSIS 3.1 Fundamental Analysis 3.2 Economic Analysis 3.3 Economic forecasting 3.4 stock Investment Decisions 3.5 Forecasting Techniques 3 3.6 Industry Analysis 65-81 3.7 Industry classification 3.8 Industry life cycle 3.9 Company Analysis 3.10Measuring Earnings 3.11 Forecasting Earnings 3.12 Applied Valuation Techniques 3.13 Graham and Dodds investor ratios. -

Security Analysis and Portfolio Management
TECEP® Test Description for FIN-321-TE SECURITY ANALYSIS AND PORTFOLIO MANAGEMENT Security Analysis and Portfolio Management presents an overview of investments with a focus on asset types, financial instruments, security markets, and mutual funds. The course provides a foundation for students entering the fields of investment analysis or portfolio management. This course examines portfolio theory, debt and equity securities, and derivative markets. It provides information on sound investment management practices, emphasizing the impact of globalization, taxes, and inflation on investments. It also provides guidance in evaluating the performance of an investment portfolio. (3 credits) ● Test format: 80 multiple choice questions (1 point each). ● Passing score: 60% (48/80 points). Your grade will be reported as CR (credit) or NC (no credit). ● Time limit: 2 hours Note: Scientific, graphing or financial calculator allowed (no phones or tablets); one sheet of scratch paper at a time, can request additional sheets. OUTCOMES ASSESSED ON THE TEST ● Discuss financial assets, financial markets, and the role of financial intermediaries ● Differentiate among equity and debt markets and stock and bond market indexes ● Assess the mechanics of various securities markets, mutual funds/investment companies, and the roles of investment bankers and brokers ● Calculate the expected rate of return from risky and risk-free investment portfolios ● Analyze portfolio theory, including measures of risk ● Discuss bond characteristics and compute bond prices and yields ● Explain equity valuation models ● Evaluate the effects of equity expense calculations, including EPS, P/E, dividends, stock betas ● Describe options and futures markets TECEP Test Description for FIN-321-TE by Thomas Edison State University is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. -

Security Analysis: an Investment Perspective
Security Analysis: An Investment Perspective Kewei Hou∗ Haitao Mo† Chen Xue‡ Lu Zhang§ Ohio State and CAFR LSU U. of Cincinnati Ohio State and NBER June 2019 Abstract The investment theory, in which the expected return varies cross-sectionally with in- vestment, expected profitability, and expected growth, is a good start to understanding Graham and Dodd’s (1934) Security Analysis. Empirically, the q5 model goes a long way toward explaining prominent equity strategies rooted in security analysis, including Frankel and Lee’s (1998) intrinsic-to-market value, Piotroski’s (2000) fundamental score, Greenblatt’s (2005) “magic formula,” Asness, Frazzini, and Pedersen’s (2019) quality- minus-junk, Buffett’s Berkshire, Bartram and Grinblatt’s (2018) agnostic analysis, as well as Penman and Zhu’s (2014, 2018) and Lewellen’s (2015) expected-return strategies. ∗Fisher College of Business, The Ohio State University, 820 Fisher Hall, 2100 Neil Avenue, Columbus OH 43210; and China Academy of Financial Research (CAFR). Tel: (614) 292-0552. E-mail: [email protected]. †E. J. Ourso College of Business, Louisiana State University, 2931 Business Education Complex, Baton Rouge, LA 70803. Tel: (225) 578-0648. E-mail: [email protected]. ‡Lindner College of Business, University of Cincinnati, 405 Lindner Hall, Cincinnati, OH 45221. Tel: (513) 556-7078. E-mail: [email protected]. §Fisher College of Business, The Ohio State University, 760A Fisher Hall, 2100 Neil Avenue, Columbus OH 43210; and NBER. Tel: (614) 292-8644. E-mail: zhanglu@fisher.osu.edu. 1 Introduction As shown in Cochrane (1991), the investment theory predicts that the expected return varies cross- sectionally, depending on firms’ investment, expected profitability, and expected growth. -

Notes from Security Analysis Sixth Edition Hardcover
Ronald R. Redfield CPA, PFS Notes to book “Security Analysis” 6th edition Written by: Benjamin Graham and David Dodd I thought these quotes from Security Analysis Sixth Edition Hardcover might be food for thought. Benjamin Graham and David Dodd first wrote security Analysis in 1934. The first edition was described by Graham as a “book that is intended for all those who have a serious interest in securities values.” The book was not designed for the investment novice. One must have an intermediate to advanced understanding of financial statements, accounting and finance for the book to be understood. The book emphasizes logical reasoning. Graham wrote, “It is the conservative investor who will need most of all to be reminded constantly of the lessons of 1931 –1933 and of previous collapses.” On Page [xiv] Seth Klarman wrote: ”Losing money, as Graham noted, can also be psychologically unsettling. Anxiety from the financial damage caused by recently experienced loss or the fear of further loss can significantly impede our ability to take advantage of the next opportunity that comes along. If an undervalued stock falls by half while the fundamentals – after checking and rechecking – are confirmed to be unchanged, we should relish the opportunity to buy significantly more “on sale.” But if our net worth has tumbled along with the share price, it may be psychologically difficult to add to the position.” On Page [xviii] Klarman wrote: ”Skepticism and judgment are always required.” “Because the value of a business depends on numerous variables, -

Value Investing Program Student Information Session
Value Investing Program Student Information Session February 20, 2020 ⧫ 12:30 p.m. Uris 301 ………………………………………………………………………………………………………………………………………… Agenda • Introduction to the Heilbrunn Center • Center Overview • Our Team • Our Courses • The Value Investing Program • Overview of the Program • Application Process • Debunking Myths • Testimonials: Q&A with current Value Investing Program students ………………………………………………………………………………………………………………………………………… 2 Heilbrunn Center: Overview ………………………………………………………………………………………………………………………………………… 3 Heilbrunn Center: Our Team Tano Santos Meredith Trivedi David L. and Elsie M. Dodd Managing Director Professor of Finance Julia Kimyagarov Caroline Reichert Director Associate Director ………………………………………………………………………………………………………………………………………… 4 Heilbrunn Center Courses (2020) Spring 2020 Tentative Fall 2020 Course Name Professor Course Name Professor Accounting for Value ~* Stephen Penman Advanced Investment Research #* Kian Ghazi Advanced Investment Research ^* Kian Ghazi Applied Value Investing #* Mark Cooper/Jonathon Luft Applied Security Analysis ~* Anuroop Duggal Applied Value Investing ~* Eric Almeraz/ David Horn Applied Value Investing #* T. Charlie Quinn Applied Value Investing (EMBA) ~+ Tom Tryforos Applied Value Investing #* Rishi Renjen/Kevin Oro-Hahn Art of Forecasting (B Term) ~* Ellen Carr Applied Value Investing #* Scott Hendrickson/ Matt Fixler Compounders *^ Anouk Dey/ Jeff Mueller Applied Value Investing ~* Anuroop Duggal Distressed Value Investing #~*+ Dan Krueger Art of Forecasting (B Term) ~* Ellen -

Security Analysis of Unified Payments Interface and Payment Apps in India
Security Analysis of Unified Payments Interface and Payment Apps in India Renuka Kumar1, Sreesh Kishore , Hao Lu1, and Atul Prakash1 1University of Michigan Abstract significant enabler. Currently, there are about 88 UPI payment apps and over 140 banks that enable transactions with those Since 2016, with a strong push from the Government of India, apps via UPI [40,41]. This paper focuses on vulnerabilities smartphone-based payment apps have become mainstream, in the design of UPI and UPI’s usage by payment apps. with over $50 billion transacted through these apps in 2018. We note that hackers are highly motivated when it comes to Many of these apps use a common infrastructure introduced money, so uncovering any design vulnerabilities in payment by the Indian government, called the Unified Payments In- systems and addressing them is crucial. For instance, a recent terface (UPI), but there has been no security analysis of this survey states a 37% increase in financial fraud and identity critical piece of infrastructure that supports money transfers. theft in 2019 in India [12]. Social engineering attacks to This paper uses a principled methodology to do a detailed extract sensitive information such as one-time passcodes and security analysis of the UPI protocol by reverse-engineering bank account numbers are common [17, 23, 34, 57, 58]. the design of this protocol through seven popular UPI apps. Payment apps, including Indian payment apps, have been We discover previously-unreported multi-factor authentica- analyzed before, with vulnerabilities discovered [9,48], and tion design-level flaws in the UPI 1.0 specification that can an Indian mobile banking service was found to have PIN lead to significant attacks when combined with an installed recovery flaws [47]. -

Security Analysis and Investment Management
M.B.A IV Semester Course 406 FM-02 SECURITY ANALYSIS AND INVESTMENT MANAGEMENT LESSONS 1 TO 6 INTERNATIONAL CENTRE FOR DISTANCE EDUCATION AND OPEN LEARNING HIMACHAL PRADESH UNIVERSITY, GYAN PATH, SUMMERHILL, SHIMLA-171005 Contents Sr. No. Topoc Page No. LESSON-1 STOCK MARKET 1 LESSON-2 NEW ISSUE MARKET 15 LESSON-3 VALUATION OF SECURITIES 26 LESSON-4 FUNDAMENTAL ANALYSIS 37 LESSON-5 TECHNICAL ANALYSIS 58 LESSON-6 PORTFOLIO MANAGEMENT 80 LESSON-1 STOCK MARKET Structure 1.0 Learning Objectives 1.1 Introduction 1.2 Financial Market 1.3 Components of Financial Market 1.4 Stock Exchange 1.5 Nature and Characteristics of Stock Exchange 1.6 Function of Stock Exchange 1.7 Advantages of Stock Exchange 1.8 Organisation of Stock Exchange in India 1.9 Operational Mechanism of Stock Exchanges 1.10 Listing of Securities 1.11 Self-check Questions 1.12 Summary 1.13 Glossary 1.14 Answers: Self-check Questions 1.15 Terminal Questions 1.16 Suggested Readings 1.0 Learning Objectives After going through this lesson the learners should be able to: 1. Understand the financial market. 2. Discuss the components of financial market. 3. Understand the function of stock market. 4. Describe the operational mechanism of the stock exchange. 1.1 Introduction Stock market or secondary market is a place where buyer and seller of listed securities come together. This market is one of the important components of financial markets. In order to understand stock markets in detail, we shall understand the structure of financial market in an economy. Sections of this unit explain briefly the financial markets, components of financial markets, nature and functions of stock market, its Organization and statutory regulations for listing securities on stock markets. -

Security Analysis by Benjamin Graham and David L. Dodd
PRAISE FOR THE SIXTH EDITION OF SECURITY ANALYSIS “The sixth edition of the iconic Security Analysis disproves the adage ‘’tis best to leave well enough alone.’ An extraordinary team of commentators, led by Seth Klarman and James Grant, bridge the gap between the sim- pler financial world of the 1930s and the more complex investment arena of the new millennium. Readers benefit from the experience and wisdom of some of the financial world’s finest practitioners and best informed market observers. The new edition of Security Analysis belongs in the library of every serious student of finance.” David F. Swensen Chief Investment Officer Yale University author of Pioneering Portfolio Management and Unconventional Success “The best of the past made current by the best of the present. Tiger Woods updates Ben Hogan. It has to be good for your game.” Jack Meyer Managing Partner and CEO Convexity Capital “Security Analysis, a 1940 classic updated by some of the greatest financial minds of our generation, is more essential than ever as a learning tool and reference book for disciplined investors today.” Jamie Dimon Chairman and CEO JPMorgan Chase “While Coca-Cola found it couldn’t improve on a time-tested classic, Seth Klarman, Jim Grant, Bruce Greenwald, et al., prove that a great book can be made even better. Seth Klarman’s preface should be required reading for all investors, and collectively, the contributing editors’ updates make for a classic in their own right. The enduring lesson is that an understand- ing of human behavior is a critical part of the process of security analysis.” Brian C.