DOCSLIB.ORG

IVC Factsheet Functions Comp Inverse

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
IVC Factsheet Functions Comp Inverse Imperial Valley College Math Lab Functions: Composition and Inverse Functions FUNCTION COMPOSITION In order to perform a composition of functions, it is essential to be familiar with function notation. If you see something of the form “푓(푥) = [expression in terms of x]”, this means that whatever you see in the parentheses following f should be substituted for x in the expression. This can include numbers, variables, other expressions, and even other functions. EXAMPLE: 푓(푥) = 4푥2 − 13푥 푓(2) = 4 ∙ 22 − 13(2) 푓(−9) = 4(−9)2 − 13(−9) 푓(푎) = 4푎2 − 13푎 푓(푐3) = 4(푐3)2 − 13푐3 푓(ℎ + 5) = 4(ℎ + 5)2 − 13(ℎ + 5) Etc. A composition of functions occurs when one function is “plugged into” another function. The notation (푓 ○푔)(푥) is pronounced “푓 of 푔 of 푥”, and it literally means 푓(푔(푥)). In other words, you “plug” the 푔(푥) function into the 푓(푥) function. Similarly, (푔 ○푓)(푥) is pronounced “푔 of 푓 of 푥”, and it literally means 푔(푓(푥)). In other words, you “plug” the 푓(푥) function into the 푔(푥) function. WARNING: Be careful not to confuse (푓 ○푔)(푥) with (푓 ∙ 푔)(푥), which means 푓(푥) ∙ 푔(푥) . EXAMPLES: 푓(푥) = 4푥2 − 13푥 푔(푥) = 2푥 + 1 a. (푓 ○푔)(푥) = 푓(푔(푥)) = 4[푔(푥)]2 − 13 ∙ 푔(푥) = 4(2푥 + 1)2 − 13(2푥 + 1) = [푠푚푝푙푓푦] … = 16푥2 − 10푥 − 9 b. (푔 ○푓)(푥) = 푔(푓(푥)) = 2 ∙ 푓(푥) + 1 = 2(4푥2 − 13푥) + 1 = 8푥2 − 26푥 + 1 A function can even be “composed” with itself: c. (푔 ○푔)(푥) = 푔(푔(푥)) = 2 ∙ 푔(푥) + 1 = 2(2푥 + 1) + 1 = 4푥 + 3 INVERSE FUNCTIONS ퟏ The notation for inverse functions can cause confusion. It is important to know that 풇−ퟏ(풙) ≠ . 풇(풙) Instead, 푓−1(푥) indicates the inverse function of 풇(풙), which can be thought of as the function that “reverses” 푓(푥) , or “undoes” everything that 푓(푥) does. EXAMPLE: Let 푓(푥) = 3푥 − 1 . In words, 푓(푥) takes a number, multiplies it by 3, and then subtracts 1 from it. The opposite or reverse of this procedure would be to add 1 to a number, then divide it by 3. For instance, 푓(ퟒ) = 3 ∙ 4 − 1 = ퟏퟏ . Input = 4 , Output = 11 In reverse, take the output 11, add 1 to it, then divide by 3: 11 + 1 = 12 12 ÷ 3 = ퟒ = input . In other words, the output became the input, and vice-versa. They switched roles! Mathematically, In each ordered pair (푥, 푦) associated with a function, the x and y “switch places”: (푥, 푦) → (푦, 푥) In the above example, (4, 11) became (11, 4) . Procedure: EXAMPLE: Given 푓(푥) , take the following steps to find 푓−1(푥): 1) 푦 = 3푥 − 1 1) Replace 푓(푥) with y in the equation 2) 푥 = 3푦 − 1 2) Swap the x and y in the equation (they “trade places”) 푥+1 3) Solve the equation for y (i.e., isolate the y) 3) 푥 + 1 = 3푦 → = 푦 3 4) Once y is isolated, replace it with 푓−1(푥) . 푥+1 1 1 4) 푓−1(푥) = or 푓−1(푥) = 푥 + Check that these values work in both directions: 3 3 3 푓(푥) = 3푥 − 1 y ( ) 1) ퟒ, ퟏퟏ –5 –16 2) (풙, 풚) (ퟏퟏ, ퟒ) 1 2 3) (풚, 풙) −1 x 4 11 푓 (푥) −1 푥+1 4) 푓 (푥) = 3 푓(푥) −1 푥+1 푓 (푥) = 3 Notice how the graphs of 풇(풙) and 풇−ퟏ(풙) are symmetric (mirror images) across the diagonal line y = x, which is the result of all the x- and y-values “trading places”. Imagine each (푥, 푦) point as “hopping” across the line y = x, becoming (푦, 푥). .
Load more

Recommended publications
  • Inverse of Exponential Functions Are Logarithmic Functions
    Math Instructional Framework Full Name Math III Unit 3 Lesson 2 Time Frame Unit Name Logarithmic Functions as Inverses of Exponential Functions Learning Task/Topics/ Task 2: How long Does It Take? Themes Task 3: The Population of Exponentia Task 4: Modeling Natural Phenomena on Earth Culminating Task: Traveling to Exponentia Standards and Elements MM3A2. Students will explore logarithmic functions as inverses of exponential functions. c. Define logarithmic functions as inverses of exponential functions. Lesson Essential Questions How can you graph the inverse of an exponential function? Activator PROBLEM 2.Task 3: The Population of Exponentia (Problem 1 could be completed prior) Work Session Inverse of Exponential Functions are Logarithmic Functions A Graph the inverse of exponential functions. B Graph logarithmic functions. See Notes Below. VOCABULARY Asymptote: A line or curve that describes the end behavior of the graph. A graph never crosses a vertical asymptote but it may cross a horizontal or oblique asymptote. Common logarithm: A logarithm with a base of 10. A common logarithm is the power, a, such that 10a = b. The common logarithm of x is written log x. For example, log 100 = 2 because 102 = 100. Exponential functions: A function of the form y = a·bx where a > 0 and either 0 < b < 1 or b > 1. Logarithmic functions: A function of the form y = logbx, with b 1 and b and x both positive. A logarithmic x function is the inverse of an exponential function. The inverse of y = b is y = logbx. Logarithm: The logarithm base b of a number x, logbx, is the power to which b must be raised to equal x.
    [Show full text]
  • The Matrix Calculus You Need for Deep Learning
    The Matrix Calculus You Need For Deep Learning Terence Parr and Jeremy Howard July 3, 2018 (We teach in University of San Francisco's MS in Data Science program and have other nefarious projects underway. You might know Terence as the creator of the ANTLR parser generator. For more material, see Jeremy's fast.ai courses and University of San Francisco's Data Institute in- person version of the deep learning course.) HTML version (The PDF and HTML were generated from markup using bookish) Abstract This paper is an attempt to explain all the matrix calculus you need in order to understand the training of deep neural networks. We assume no math knowledge beyond what you learned in calculus 1, and provide links to help you refresh the necessary math where needed. Note that you do not need to understand this material before you start learning to train and use deep learning in practice; rather, this material is for those who are already familiar with the basics of neural networks, and wish to deepen their understanding of the underlying math. Don't worry if you get stuck at some point along the way|just go back and reread the previous section, and try writing down and working through some examples. And if you're still stuck, we're happy to answer your questions in the Theory category at forums.fast.ai. Note: There is a reference section at the end of the paper summarizing all the key matrix calculus rules and terminology discussed here. arXiv:1802.01528v3 [cs.LG] 2 Jul 2018 1 Contents 1 Introduction 3 2 Review: Scalar derivative rules4 3 Introduction to vector calculus and partial derivatives5 4 Matrix calculus 6 4.1 Generalization of the Jacobian .
    [Show full text]
  • The Logic of Recursive Equations Author(S): A
    The Logic of Recursive Equations Author(s): A. J. C. Hurkens, Monica McArthur, Yiannis N. Moschovakis, Lawrence S. Moss, Glen T. Whitney Source: The Journal of Symbolic Logic, Vol. 63, No. 2 (Jun., 1998), pp. 451-478 Published by: Association for Symbolic Logic Stable URL: http://www.jstor.org/stable/2586843 . Accessed: 19/09/2011 22:53 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Association for Symbolic Logic is collaborating with JSTOR to digitize, preserve and extend access to The Journal of Symbolic Logic. http://www.jstor.org THE JOURNAL OF SYMBOLIC LOGIC Volume 63, Number 2, June 1998 THE LOGIC OF RECURSIVE EQUATIONS A. J. C. HURKENS, MONICA McARTHUR, YIANNIS N. MOSCHOVAKIS, LAWRENCE S. MOSS, AND GLEN T. WHITNEY Abstract. We study logical systems for reasoning about equations involving recursive definitions. In particular, we are interested in "propositional" fragments of the functional language of recursion FLR [18, 17], i.e., without the value passing or abstraction allowed in FLR. The 'pure," propositional fragment FLRo turns out to coincide with the iteration theories of [1]. Our main focus here concerns the sharp contrast between the simple class of valid identities and the very complex consequence relation over several natural classes of models.
    [Show full text]
  • 5.7 Inverses and Radical Functions Finding the Inverse Of
    SECTION 5.7 iNverses ANd rAdicAl fuNctioNs 435 leARnIng ObjeCTIveS In this section, you will: • Find the inverse of an invertible polynomial function. • Restrict the domain to find the inverse of a polynomial function. 5.7 InveRSeS And RAdICAl FUnCTIOnS A mound of gravel is in the shape of a cone with the height equal to twice the radius. Figure 1 The volume is found using a formula from elementary geometry. __1 V = πr 2 h 3 __1 = πr 2(2r) 3 __2 = πr 3 3 We have written the volume V in terms of the radius r. However, in some cases, we may start out with the volume and want to find the radius. For example: A customer purchases 100 cubic feet of gravel to construct a cone shape mound with a height twice the radius. What are the radius and height of the new cone? To answer this question, we use the formula ____ 3 3V r = ___ √ 2π This function is the inverse of the formula for V in terms of r. In this section, we will explore the inverses of polynomial and rational functions and in particular the radical functions we encounter in the process. Finding the Inverse of a Polynomial Function Two functions f and g are inverse functions if for every coordinate pair in f, (a, b), there exists a corresponding coordinate pair in the inverse function, g, (b, a). In other words, the coordinate pairs of the inverse functions have the input and output interchanged. Only one-to-one functions have inverses. Recall that a one-to-one function has a unique output value for each input value and passes the horizontal line test.
    [Show full text]
  • Inverse Trigonometric Functions
    Chapter 2 INVERSE TRIGONOMETRIC FUNCTIONS vMathematics, in general, is fundamentally the science of self-evident things. — FELIX KLEIN v 2.1 Introduction In Chapter 1, we have studied that the inverse of a function f, denoted by f–1, exists if f is one-one and onto. There are many functions which are not one-one, onto or both and hence we can not talk of their inverses. In Class XI, we studied that trigonometric functions are not one-one and onto over their natural domains and ranges and hence their inverses do not exist. In this chapter, we shall study about the restrictions on domains and ranges of trigonometric functions which ensure the existence of their inverses and observe their behaviour through graphical representations. Besides, some elementary properties will also be discussed. The inverse trigonometric functions play an important Aryabhata role in calculus for they serve to define many integrals. (476-550 A. D.) The concepts of inverse trigonometric functions is also used in science and engineering. 2.2 Basic Concepts In Class XI, we have studied trigonometric functions, which are defined as follows: sine function, i.e., sine : R → [– 1, 1] cosine function, i.e., cos : R → [– 1, 1] π tangent function, i.e., tan : R – { x : x = (2n + 1) , n ∈ Z} → R 2 cotangent function, i.e., cot : R – { x : x = nπ, n ∈ Z} → R π secant function, i.e., sec : R – { x : x = (2n + 1) , n ∈ Z} → R – (– 1, 1) 2 cosecant function, i.e., cosec : R – { x : x = nπ, n ∈ Z} → R – (– 1, 1) 2021-22 34 MATHEMATICS We have also learnt in Chapter 1 that if f : X→Y such that f(x) = y is one-one and onto, then we can define a unique function g : Y→X such that g(y) = x, where x ∈ X and y = f(x), y ∈ Y.
    [Show full text]
  • Monoids: Theme and Variations (Functional Pearl)
    University of Pennsylvania ScholarlyCommons Departmental Papers (CIS) Department of Computer & Information Science 7-2012 Monoids: Theme and Variations (Functional Pearl) Brent A. Yorgey University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/cis_papers Part of the Programming Languages and Compilers Commons, Software Engineering Commons, and the Theory and Algorithms Commons Recommended Citation Brent A. Yorgey, "Monoids: Theme and Variations (Functional Pearl)", . July 2012. This paper is posted at ScholarlyCommons. https://repository.upenn.edu/cis_papers/762 For more information, please contact [email protected]. Monoids: Theme and Variations (Functional Pearl) Abstract The monoid is a humble algebraic structure, at first glance ve en downright boring. However, there’s much more to monoids than meets the eye. Using examples taken from the diagrams vector graphics framework as a case study, I demonstrate the power and beauty of monoids for library design. The paper begins with an extremely simple model of diagrams and proceeds through a series of incremental variations, all related somehow to the central theme of monoids. Along the way, I illustrate the power of compositional semantics; why you should also pay attention to the monoid’s even humbler cousin, the semigroup; monoid homomorphisms; and monoid actions. Keywords monoid, homomorphism, monoid action, EDSL Disciplines Programming Languages and Compilers | Software Engineering | Theory and Algorithms This conference paper is available at ScholarlyCommons: https://repository.upenn.edu/cis_papers/762 Monoids: Theme and Variations (Functional Pearl) Brent A. Yorgey University of Pennsylvania [email protected] Abstract The monoid is a humble algebraic structure, at first glance even downright boring.
    [Show full text]
  • Calculus Formulas and Theorems
    Formulas and Theorems for Reference I. Tbigonometric Formulas l. sin2d+c,cis2d:1 sec2d l*cot20:<:sc:20 +.I sin(-d) : -sitt0 t,rs(-//) = t r1sl/ : -tallH 7. sin(A* B) :sitrAcosB*silBcosA 8. : siri A cos B - siu B <:os,;l 9. cos(A+ B) - cos,4cos B - siuA siriB 10. cos(A- B) : cosA cosB + silrA sirrB 11. 2 sirrd t:osd 12. <'os20- coS2(i - siu20 : 2<'os2o - I - 1 - 2sin20 I 13. tan d : <.rft0 (:ost/ I 14. <:ol0 : sirrd tattH 1 15. (:OS I/ 1 16. cscd - ri" 6i /F tl r(. cos[I ^ -el : sitt d \l 18. -01 : COSA 215 216 Formulas and Theorems II. Differentiation Formulas !(r") - trr:"-1 Q,:I' ]tra-fg'+gf' gJ'-,f g' - * (i) ,l' ,I - (tt(.r))9'(.,') ,i;.[tyt.rt) l'' d, \ (sttt rrJ .* ('oqI' .7, tJ, \ . ./ stll lr dr. l('os J { 1a,,,t,:r) - .,' o.t "11'2 1(<,ot.r') - (,.(,2.r' Q:T rl , (sc'c:.r'J: sPl'.r tall 11 ,7, d, - (<:s<t.r,; - (ls(].]'(rot;.r fr("'),t -.'' ,1 - fr(u") o,'ltrc ,l ,, 1 ' tlll ri - (l.t' .f d,^ --: I -iAl'CSllLl'l t!.r' J1 - rz 1(Arcsi' r) : oT Il12 Formulas and Theorems 2I7 III. Integration Formulas 1. ,f "or:artC 2. [\0,-trrlrl *(' .t "r 3. [,' ,t.,: r^x| (' ,I 4. In' a,,: lL , ,' .l 111Q 5. In., a.r: .rhr.r' .r r (' ,l f 6. sirr.r d.r' - ( os.r'-t C ./ 7. /.,,.r' dr : sitr.i'| (' .t 8. tl:r:hr sec,rl+ C or ln Jccrsrl+ C ,f'r^rr f 9.
    [Show full text]
  • Contents 3 Homomorphisms, Ideals, and Quotients
    Ring Theory (part 3): Homomorphisms, Ideals, and Quotients (by Evan Dummit, 2018, v. 1.01) Contents 3 Homomorphisms, Ideals, and Quotients 1 3.1 Ring Isomorphisms and Homomorphisms . 1 3.1.1 Ring Isomorphisms . 1 3.1.2 Ring Homomorphisms . 4 3.2 Ideals and Quotient Rings . 7 3.2.1 Ideals . 8 3.2.2 Quotient Rings . 9 3.2.3 Homomorphisms and Quotient Rings . 11 3.3 Properties of Ideals . 13 3.3.1 The Isomorphism Theorems . 13 3.3.2 Generation of Ideals . 14 3.3.3 Maximal and Prime Ideals . 17 3.3.4 The Chinese Remainder Theorem . 20 3.4 Rings of Fractions . 21 3 Homomorphisms, Ideals, and Quotients In this chapter, we will examine some more intricate properties of general rings. We begin with a discussion of isomorphisms, which provide a way of identifying two rings whose structures are identical, and then examine the broader class of ring homomorphisms, which are the structure-preserving functions from one ring to another. Next, we study ideals and quotient rings, which provide the most general version of modular arithmetic in a ring, and which are fundamentally connected with ring homomorphisms. We close with a detailed study of the structure of ideals and quotients in commutative rings with 1. 3.1 Ring Isomorphisms and Homomorphisms • We begin our study with a discussion of structure-preserving maps between rings. 3.1.1 Ring Isomorphisms • We have encountered several examples of rings with very similar structures. • For example, consider the two rings R = Z=6Z and S = (Z=2Z) × (Z=3Z).
    [Show full text]
  • On CCZ-Equivalence of the Inverse Function
    1 On CCZ-equivalence of the inverse function Lukas K¨olsch −1 Abstract—The inverse function x 7→ x on F2n is one of the graph of F , denoted by G = (x, F (x)): x F n , to 1 F1 { 1 ∈ 2 } most studied functions in cryptography due to its widespread the graph of F2. use as an S-box in block ciphers like AES. In this paper, we show that, if n ≥ 5, every function that is CCZ-equivalent It is obvious that two functions that are affine equivalent are to the inverse function is already EA-equivalent to it. This also EA-equivalent. Furthermore, two EA-equivalent func- confirms a conjecture by Budaghyan, Calderini and Villa. We tions are also CCZ-equivalent. In general, the concepts of also prove that every permutation that is CCZ-equivalent to the inverse function is already affine equivalent to it. The majority CCZ-equivalence and EA equivalence do differ, for example of the paper is devoted to proving that there is no permutation a bijective function is always CCZ-equivalent to its compo- −1 polynomial of the form L1(x )+ L2(x) over F2n if n ≥ 5, sitional inverse, which is not the case for EA-equivalence. where L1, L2 are nonzero linear functions. In the proof, we Note also that the size of the image set is invariant under combine Kloosterman sums, quadratic forms and tools from affine equivalence, which is generally not the case for the additive combinatorics. other two more general notions. Index Terms —Inverse function, CCZ-equivalence, EA- Particularly well studied are APN monomials, a list of all equivalence, S-boxes, permutation polynomials.
    [Show full text]
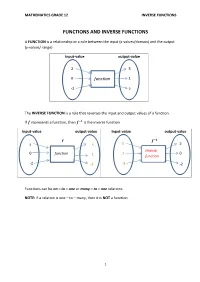
  • Grade 12 Mathematics Inverse Functions
    MATHEMATICS GRADE 12 INVERSE FUNCTIONS FUNCTIONS AND INVERSE FUNCTIONS A FUNCTION is a relationship or a rule between the input (x-values/domain) and the output (y-values/ range) Input-value output-value 2 5 0 function 1 -2 2 The INVERSE FUNCTION is a rule that reverses the input and output values of a function. If represents a function, then is the inverse function. Input-value output-value Input-value output-value 풇 풇 ퟏ 2 5 5 2 Inverse 0 function 1 0 1 function -2 -3 -3 -2 Functions can be on – to – one or many – to – one relations. NOTE: if a relation is one – to – many, then it is NOT a function. 1 MATHEMATICS GRADE 12 INVERSE FUNCTIONS HOW TO DETERMINE WHETHER THE GRAPH IS A FUNCTION OR NOT i. Vertical – line test: The vertical –line test is used to determine whether a graph is a function or not a function. To determine whether a graph is a function, draw a vertical line parallel to the y-axis or perpendicular to the x- axis. If the line intersects the graph once then graph is a function. If the line intersects the graph more than once then the relation is not a function of x. Because functions are single-valued relations and a particular x-value is mapped onto one and only one y-value. Function not a function (one to many relation) TEST FOR ONE –TO– ONE FUNCTION ii. Horizontal – line test The horizontal – line test is used to determine whether a function is a one-to-one function.
    [Show full text]
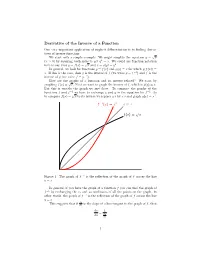
  • Derivative of the Inverse of a Function One Very Important Application of Implicit Differentiation Is to finding Deriva­ Tives of Inverse Functions
    Derivative of the Inverse of a Function One very important application of implicit differentiation is to finding deriva­ tives of inverse functions. We start with a simple example. We might simplify the equation y = px (x > 0) by squaring both sides to get y2 = x. We could use function notation here to say that y = f(x) = px and x = g(y) = y2. In general, we look for functions y = f(x) and g(y) = x for which g(f(x)) = x. If this is the case, then g is the inverse of f (we write g = f −1) and f is the inverse of g (we write f = g−1). How are the graphs of a function and its inverse related? We start by graphing f(x) = px. Next we want to graph the inverse of f, which is g(y) = x. But this is exactly the graph we just drew. To compare the graphs of the functions f and f −1 we have to exchange x and y in the equation for f −1 . So to compare f(x) = px to its inverse we replace y’s by x’s and graph g(x) = x2. 1 2 f − (x)=x y = x f(x)=√x −1 Figure 1: The graph of f is the reflection of the graph of f across the line y = x In general, if you have the graph of a function f you can find the graph of −1 f by exchanging the x- and y-coordinates of all the points on the graph.
    [Show full text]
  • Math 311 - Introduction to Proof and Abstract Mathematics Group Assignment # 15 Name: Due: at the End of Class on Tuesday, March 26Th
    Math 311 - Introduction to Proof and Abstract Mathematics Group Assignment # 15 Name: Due: At the end of class on Tuesday, March 26th More on Functions: Definition 5.1.7: Let A, B, C, and D be sets. Let f : A B and g : C D be functions. Then f = g if: → → A = C and B = D • For all x A, f(x)= g(x). • ∈ Intuitively speaking, this definition tells us that a function is determined by its underlying correspondence, not its specific formula or rule. Another way to think of this is that a function is determined by the set of points that occur on its graph. 1. Give a specific example of two functions that are defined by different rules (or formulas) but that are equal as functions. 2. Consider the functions f(x)= x and g(x)= √x2. Find: (a) A domain for which these functions are equal. (b) A domain for which these functions are not equal. Definition 5.1.9 Let X be a set. The identity function on X is the function IX : X X defined by, for all x X, → ∈ IX (x)= x. 3. Let f(x)= x cos(2πx). Prove that f(x) is the identity function when X = Z but not when X = R. Definition 5.1.10 Let n Z with n 0, and let a0,a1, ,an R such that an = 0. The function p : R R is a ∈ ≥ ··· ∈ 6 n n−1 → polynomial of degree n with real coefficients a0,a1, ,an if for all x R, p(x)= anx +an−1x + +a1x+a0.
    [Show full text]