DOCSLIB.ORG

INVERSE FUNCTION THEOREM and SURFACES in Rn Let F ∈ C K(U;Rn)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
INVERSE FUNCTION THEOREM and SURFACES in Rn Let F ∈ C K(U;Rn) INVERSE FUNCTION THEOREM and SURFACES IN Rn Let f 2 Ck(U; Rn), with U ⊂ Rn open (k ≥ 1). Assume df(a) 2 GL(Rn), where a 2 U. The Inverse Function Theorem says there is an open n n neighborhood V ⊂ U of a in R so that fjV : V ! R is a homeomorphism onto its image W = f(V ), an open subset of Rn; the inverse g = f −1 : W ! V is a Ck map. The inverse function theorem as an existence theorem. Given f : X ! Y (X; Y Banach spaces) and y 2 Y , we seek to solve the nonlinear equation: f(x) = y: The idea is that if f is close (in some sense) to a linear operator A 2 L(X; Y ) for which the problem is uniquely solvable, and (for a given b 2 Y ) we happen to know a solution a 2 X to f(x) = b, then for values y close to b the equation should have a unique solution (close to a). For example, suppose f has the form f(x) = Ax + φ(x), where A 2 L(X; Y ) is invertible (with bounded inverse) and φ : X ! Y is Lipschitz, with a small Lipschitz constant Lip(φ). Then to solve Ax + φ(x) = y assuming the linear problem Av = w can be solved uniquely for any w 2 Y −1 (that is, A is invertible, and jvjX ≤ CjwjY , where C = jjA jj) we compute successive approximations, starting from an arbitrary a 2 X and solving the sequence of linear problems with given `right-hand side': Ax1 = y − φ(a); Ax2 = y − φ(x1); Ax3 = y − φ(x2); ··· Convergence of (xn) is established by setting this up as a fixed point problem, for F (x) = A−1[y − φ(x)]: x1 = F (a); x2 = F (x1); ··· Convergence to a fixed point is guaranteed provided F is a contraction of X: jF (x) − F (¯x)j ≤ λjx − x¯j, where 0 < λ < 1. Since jF (x) − F (¯x)j = jA−1[φ(x) − φ(¯x)]j; it suffices to require Lip(φ) < 1=jjA−1jj: Then the estimate (for two solutions of f(x) = y; f(¯x) =y; ¯ y; y¯ 2 Y : jx − x¯j = jA−1[y − y¯] − A−1[φ(x) − φ(¯x)]j ≤ jA−1j(jy − y¯j + Lip(φ)jx − x¯j); 1 (1 − λ)jx − x¯j ≤ jA−1jjy − y¯j; λ = jA−1jLip(φ) < 1 shows that the inverse map g(y) = x is Lipschitz, with constant Lip(g) ≤ jA−1j=(1 − λ). We recall here the standard fixed point theorem for contractions. Contractions have unique fixed points. Let (X; d) be a complete metric space, F : X ! X a λ-contraction, where 0 < λ < 1: d(F (x);F (y)) ≤ λd(x; y); 8x; y 2 X. Then F has a unique fixed point p 2 X, which is globally attracting (F n(x) ! p, 8x 2 X.) n Proof. Let x 2 X. For the sequence of iterates xn = F (x), the contrac- m m tion property easily implies d(xm+1; xm) ≤ λ d(x1; x) := λ δ, and then if n > m ≥ N: λN d(x ; x ) ≤ d(x ; x ) + : : : d(x ; x ) ≤ (λn−1 + : : : λm)δ ≤ δ; n m n n−1 m+1 m 1 − λ so (xn) is a Cauchy sequence, and xn ! p 2 X. Then p is a fixed point: d(F (p); p) ≤ d(F (p);F (xn)) + d(xn+1; p) ≤ λd(xn; p) + d(xn+1; p) ! 0: It follows easily from the contraction property that F can only have one fixed point. Typically the `perturbation' φ of the invertible linear map A will satisfy a Lipschitz condition only in some open set U ⊂ X. Then given a point b 2 Y for which the problem has a unique solution a 2 U (that is, f(a) = b) and a nearby point y 2 Y , we seek solutions x 2 B¯r(a), (closed ball), where r > 0 is small enough that this ball is contained in U. The successive approximations scheme still works, provided we guarantee this ball is invariant under F . So −1 we estimate, for x 2 B¯r(a) (using a = A [b − φ(a)]): jF (x) − aj = jA−1[y − φ(x)] − aj = A−1[y − b] − A−1[φ(x) − φ(a)]j ≤ jA−1j(jy − bj + Lip(φ)jx − aj) ≤ jA−1j(s + Lip(φ)r); and this is bounded above by r provided we pick y 2 Bs(b) (open ball in (1−λ)r −1 Y ), where s ≤ jA−1j (with λ = jA jLip(φ) < 1 as before). We summarize as follows: 2 Proposition 1. Perturbations of invertible linear maps are homeomorphisms. Let f : U ! Y (U ⊂ X open) have the form f(x) = Ax + φ(x), where A 2 L(X; Y ) is boundedly invertible and φ is Lipschitz with Lip(φ) < jjA−1jj−1. Then V = f(U) is open in Y , and f : U ! V is a homeomorphism with Lipschitz inverse. If U = X, f is a homeomorphism onto Y (with Lipschitz inverse). Exercise 1. Let f : R ! R have the form f(x) = ax + g(x), where a > 0 and g is Lipschitz on R, with constant M satisfying M < a. (i) Show that f is injective. (ii) Show that f is surjective. Remark use only the definitions, quoting no theorems other than the fixed point theorem for contractions in part (ii). A property of C1 maps. Let f : U ! Rm be C1, U ⊂ Rn open. Given a 2 U, we have the remainder: ra(x) = f(x) − f(a) − df(a)[x − a]; x 2 U: n m Then dra(x) = df(x) − df(a) is continuous from U to L(R ;R ), and van- ishes at x = a. We conclude that, for any > 0, there exists an r > 0 so that jjdra(x)jj ≤ if x 2 Br(a). By the Mean Value Inequality: jjra(x) − ra(y)jj ≤ jjx − yjj; for x; y 2 Br(a): In other words: ra is a Lipschitz map with arbitrarily small Lipschitz con- stant, in a sufficiently small neighborhood of a. Equivalently: r (x) − r (y) lim a a = 0: x!a;y!a jjx − yjj Note that this is equivalent to saying that, for all x; y 2 Br(a)(setting ra(x; y) = ra(x) − ra(y)): r( x; y) f(y) − f(x) = df(a)[y − x] + r(x; y); lim a = 0: x!a;y!a jjx − yjj Remark: Note that only continuity of df at a is used. Conversely, if this condition holds at a 2 U, then df is continuous at a. To see this, combining: f(x) − f(y) = df(a)[x − y] + ra(y; x); f(y) − f(x) = df(x)[y − x] + rx(y); 3 we find: (df(x) − df(a))[y − x] = −[ra(y; x) + rx(y)]. Given > 0, we find ρ > 0 and for each x 2 U, 0 < ηx < ρ so that: jjra(x; y)jj ≤ jjy−xjj for x; y 2 B2ρ(a); jjy−xjj ≤ ηx ) jjrx(y)jj ≤ jjy−xjj: Let x 2 U satisfy jjx−ajj ≤ ρ, and let u 2 Rn be a unit vector. Then letting y = x + ηxu we have: x; y 2 B2ρ(a) and jjy − xjj ≤ ηx, so n ηxjj(df(x)−df(a))[u]jj ≤ jjra(x; y)jj+jjrx(y)jj ≤ 2ηx; 8u 2 R with jjujj = 1: Thus, for the operator norm in L(Rn; Rm): jjdf(x) − df(a)jj ≤ 2, establishing continuity of df at a. Turning to the case m = n, let f 2 C1(U; Rn), with df(a) 2 GL(Rn) (that is, df(a) is an invertible linear map) for all a 2 U. Then: f(x) = f(a)+df(a)[x−a]+ra(x) = df(a)[x]+φ(x); φ(x) = f(a)−df(a)[a]+ra(x); so φ is Lipschitz in U if and only if ra is (with the same Lipschitz constant.) Thus φ has arbitrarily small Lipschitz constant in a sufficiently small ball at a, assuming f 2 C1. This motivates the hypothesis in the statement of the Inverse Mapping Theorem. Inverse Mapping Theorem. Let f : U ! Rn (U ⊂ Rn open) be of class C1 in U. Let a 2 U, and assume df(a) 2 GL(Rn) (that is, df(a) is an isomorphism.) Then there exists a neighborhood V ⊂ U of a so that: (i) The restriction fjV is a bi-Lipschitz homeomorphism onto its image W = f(V ), and W is open in Rn. (ii) The inverse map g = f −1 : W ! V is differentiable in W , and dg(y) = [df(g(y)]−1, for all y 2 W ; (iii) If f 2 Ck(U; Rn) (with k ≥ 1) then g 2 Ck(W ; Rn). 1 Proof. (i): Since f is C , we may find an open ball V = Br(a) so that for x; x¯ in V : f(x) = f(a)+df(a)[x−a]+r(x); where jr(x)−r(¯x)j ≤ λjx−x¯j with λjdf(a)−1j < 1: In other words (since f(a) − df(a)[a] is a constant) in this ball V , f is a per- turbation of the isomorphism df(a). Conclusion (i) follows from Proposition 1. 4 Prior to proving (ii), we consider a general result on differentiability of the inverse (of a homeomorphism). Note that the inverse of the homeomor- phism f(x) = x3 of the real line is not differentiable at x = 0.
Load more

Recommended publications
  • Inverse of Exponential Functions Are Logarithmic Functions
    Math Instructional Framework Full Name Math III Unit 3 Lesson 2 Time Frame Unit Name Logarithmic Functions as Inverses of Exponential Functions Learning Task/Topics/ Task 2: How long Does It Take? Themes Task 3: The Population of Exponentia Task 4: Modeling Natural Phenomena on Earth Culminating Task: Traveling to Exponentia Standards and Elements MM3A2. Students will explore logarithmic functions as inverses of exponential functions. c. Define logarithmic functions as inverses of exponential functions. Lesson Essential Questions How can you graph the inverse of an exponential function? Activator PROBLEM 2.Task 3: The Population of Exponentia (Problem 1 could be completed prior) Work Session Inverse of Exponential Functions are Logarithmic Functions A Graph the inverse of exponential functions. B Graph logarithmic functions. See Notes Below. VOCABULARY Asymptote: A line or curve that describes the end behavior of the graph. A graph never crosses a vertical asymptote but it may cross a horizontal or oblique asymptote. Common logarithm: A logarithm with a base of 10. A common logarithm is the power, a, such that 10a = b. The common logarithm of x is written log x. For example, log 100 = 2 because 102 = 100. Exponential functions: A function of the form y = a·bx where a > 0 and either 0 < b < 1 or b > 1. Logarithmic functions: A function of the form y = logbx, with b 1 and b and x both positive. A logarithmic x function is the inverse of an exponential function. The inverse of y = b is y = logbx. Logarithm: The logarithm base b of a number x, logbx, is the power to which b must be raised to equal x.
    [Show full text]
  • IVC Factsheet Functions Comp Inverse
    Imperial Valley College Math Lab Functions: Composition and Inverse Functions FUNCTION COMPOSITION In order to perform a composition of functions, it is essential to be familiar with function notation. If you see something of the form “푓(푥) = [expression in terms of x]”, this means that whatever you see in the parentheses following f should be substituted for x in the expression. This can include numbers, variables, other expressions, and even other functions. EXAMPLE: 푓(푥) = 4푥2 − 13푥 푓(2) = 4 ∙ 22 − 13(2) 푓(−9) = 4(−9)2 − 13(−9) 푓(푎) = 4푎2 − 13푎 푓(푐3) = 4(푐3)2 − 13푐3 푓(ℎ + 5) = 4(ℎ + 5)2 − 13(ℎ + 5) Etc. A composition of functions occurs when one function is “plugged into” another function. The notation (푓 ○푔)(푥) is pronounced “푓 of 푔 of 푥”, and it literally means 푓(푔(푥)). In other words, you “plug” the 푔(푥) function into the 푓(푥) function. Similarly, (푔 ○푓)(푥) is pronounced “푔 of 푓 of 푥”, and it literally means 푔(푓(푥)). In other words, you “plug” the 푓(푥) function into the 푔(푥) function. WARNING: Be careful not to confuse (푓 ○푔)(푥) with (푓 ∙ 푔)(푥), which means 푓(푥) ∙ 푔(푥) . EXAMPLES: 푓(푥) = 4푥2 − 13푥 푔(푥) = 2푥 + 1 a. (푓 ○푔)(푥) = 푓(푔(푥)) = 4[푔(푥)]2 − 13 ∙ 푔(푥) = 4(2푥 + 1)2 − 13(2푥 + 1) = [푠푚푝푙푓푦] … = 16푥2 − 10푥 − 9 b. (푔 ○푓)(푥) = 푔(푓(푥)) = 2 ∙ 푓(푥) + 1 = 2(4푥2 − 13푥) + 1 = 8푥2 − 26푥 + 1 A function can even be “composed” with itself: c.
    [Show full text]
  • 5.7 Inverses and Radical Functions Finding the Inverse Of
    SECTION 5.7 iNverses ANd rAdicAl fuNctioNs 435 leARnIng ObjeCTIveS In this section, you will: • Find the inverse of an invertible polynomial function. • Restrict the domain to find the inverse of a polynomial function. 5.7 InveRSeS And RAdICAl FUnCTIOnS A mound of gravel is in the shape of a cone with the height equal to twice the radius. Figure 1 The volume is found using a formula from elementary geometry. __1 V = πr 2 h 3 __1 = πr 2(2r) 3 __2 = πr 3 3 We have written the volume V in terms of the radius r. However, in some cases, we may start out with the volume and want to find the radius. For example: A customer purchases 100 cubic feet of gravel to construct a cone shape mound with a height twice the radius. What are the radius and height of the new cone? To answer this question, we use the formula ____ 3 3V r = ___ √ 2π This function is the inverse of the formula for V in terms of r. In this section, we will explore the inverses of polynomial and rational functions and in particular the radical functions we encounter in the process. Finding the Inverse of a Polynomial Function Two functions f and g are inverse functions if for every coordinate pair in f, (a, b), there exists a corresponding coordinate pair in the inverse function, g, (b, a). In other words, the coordinate pairs of the inverse functions have the input and output interchanged. Only one-to-one functions have inverses. Recall that a one-to-one function has a unique output value for each input value and passes the horizontal line test.
    [Show full text]
  • Inverse Trigonometric Functions
    Chapter 2 INVERSE TRIGONOMETRIC FUNCTIONS vMathematics, in general, is fundamentally the science of self-evident things. — FELIX KLEIN v 2.1 Introduction In Chapter 1, we have studied that the inverse of a function f, denoted by f–1, exists if f is one-one and onto. There are many functions which are not one-one, onto or both and hence we can not talk of their inverses. In Class XI, we studied that trigonometric functions are not one-one and onto over their natural domains and ranges and hence their inverses do not exist. In this chapter, we shall study about the restrictions on domains and ranges of trigonometric functions which ensure the existence of their inverses and observe their behaviour through graphical representations. Besides, some elementary properties will also be discussed. The inverse trigonometric functions play an important Aryabhata role in calculus for they serve to define many integrals. (476-550 A. D.) The concepts of inverse trigonometric functions is also used in science and engineering. 2.2 Basic Concepts In Class XI, we have studied trigonometric functions, which are defined as follows: sine function, i.e., sine : R → [– 1, 1] cosine function, i.e., cos : R → [– 1, 1] π tangent function, i.e., tan : R – { x : x = (2n + 1) , n ∈ Z} → R 2 cotangent function, i.e., cot : R – { x : x = nπ, n ∈ Z} → R π secant function, i.e., sec : R – { x : x = (2n + 1) , n ∈ Z} → R – (– 1, 1) 2 cosecant function, i.e., cosec : R – { x : x = nπ, n ∈ Z} → R – (– 1, 1) 2021-22 34 MATHEMATICS We have also learnt in Chapter 1 that if f : X→Y such that f(x) = y is one-one and onto, then we can define a unique function g : Y→X such that g(y) = x, where x ∈ X and y = f(x), y ∈ Y.
    [Show full text]
  • Calculus Formulas and Theorems
    Formulas and Theorems for Reference I. Tbigonometric Formulas l. sin2d+c,cis2d:1 sec2d l*cot20:<:sc:20 +.I sin(-d) : -sitt0 t,rs(-//) = t r1sl/ : -tallH 7. sin(A* B) :sitrAcosB*silBcosA 8. : siri A cos B - siu B <:os,;l 9. cos(A+ B) - cos,4cos B - siuA siriB 10. cos(A- B) : cosA cosB + silrA sirrB 11. 2 sirrd t:osd 12. <'os20- coS2(i - siu20 : 2<'os2o - I - 1 - 2sin20 I 13. tan d : <.rft0 (:ost/ I 14. <:ol0 : sirrd tattH 1 15. (:OS I/ 1 16. cscd - ri" 6i /F tl r(. cos[I ^ -el : sitt d \l 18. -01 : COSA 215 216 Formulas and Theorems II. Differentiation Formulas !(r") - trr:"-1 Q,:I' ]tra-fg'+gf' gJ'-,f g' - * (i) ,l' ,I - (tt(.r))9'(.,') ,i;.[tyt.rt) l'' d, \ (sttt rrJ .* ('oqI' .7, tJ, \ . ./ stll lr dr. l('os J { 1a,,,t,:r) - .,' o.t "11'2 1(<,ot.r') - (,.(,2.r' Q:T rl , (sc'c:.r'J: sPl'.r tall 11 ,7, d, - (<:s<t.r,; - (ls(].]'(rot;.r fr("'),t -.'' ,1 - fr(u") o,'ltrc ,l ,, 1 ' tlll ri - (l.t' .f d,^ --: I -iAl'CSllLl'l t!.r' J1 - rz 1(Arcsi' r) : oT Il12 Formulas and Theorems 2I7 III. Integration Formulas 1. ,f "or:artC 2. [\0,-trrlrl *(' .t "r 3. [,' ,t.,: r^x| (' ,I 4. In' a,,: lL , ,' .l 111Q 5. In., a.r: .rhr.r' .r r (' ,l f 6. sirr.r d.r' - ( os.r'-t C ./ 7. /.,,.r' dr : sitr.i'| (' .t 8. tl:r:hr sec,rl+ C or ln Jccrsrl+ C ,f'r^rr f 9.
    [Show full text]
  • On CCZ-Equivalence of the Inverse Function
    1 On CCZ-equivalence of the inverse function Lukas K¨olsch −1 Abstract—The inverse function x 7→ x on F2n is one of the graph of F , denoted by G = (x, F (x)): x F n , to 1 F1 { 1 ∈ 2 } most studied functions in cryptography due to its widespread the graph of F2. use as an S-box in block ciphers like AES. In this paper, we show that, if n ≥ 5, every function that is CCZ-equivalent It is obvious that two functions that are affine equivalent are to the inverse function is already EA-equivalent to it. This also EA-equivalent. Furthermore, two EA-equivalent func- confirms a conjecture by Budaghyan, Calderini and Villa. We tions are also CCZ-equivalent. In general, the concepts of also prove that every permutation that is CCZ-equivalent to the inverse function is already affine equivalent to it. The majority CCZ-equivalence and EA equivalence do differ, for example of the paper is devoted to proving that there is no permutation a bijective function is always CCZ-equivalent to its compo- −1 polynomial of the form L1(x )+ L2(x) over F2n if n ≥ 5, sitional inverse, which is not the case for EA-equivalence. where L1, L2 are nonzero linear functions. In the proof, we Note also that the size of the image set is invariant under combine Kloosterman sums, quadratic forms and tools from affine equivalence, which is generally not the case for the additive combinatorics. other two more general notions. Index Terms —Inverse function, CCZ-equivalence, EA- Particularly well studied are APN monomials, a list of all equivalence, S-boxes, permutation polynomials.
    [Show full text]
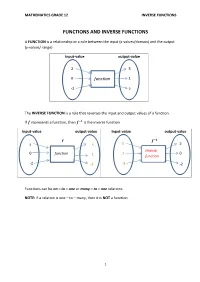
  • Grade 12 Mathematics Inverse Functions
    MATHEMATICS GRADE 12 INVERSE FUNCTIONS FUNCTIONS AND INVERSE FUNCTIONS A FUNCTION is a relationship or a rule between the input (x-values/domain) and the output (y-values/ range) Input-value output-value 2 5 0 function 1 -2 2 The INVERSE FUNCTION is a rule that reverses the input and output values of a function. If represents a function, then is the inverse function. Input-value output-value Input-value output-value 풇 풇 ퟏ 2 5 5 2 Inverse 0 function 1 0 1 function -2 -3 -3 -2 Functions can be on – to – one or many – to – one relations. NOTE: if a relation is one – to – many, then it is NOT a function. 1 MATHEMATICS GRADE 12 INVERSE FUNCTIONS HOW TO DETERMINE WHETHER THE GRAPH IS A FUNCTION OR NOT i. Vertical – line test: The vertical –line test is used to determine whether a graph is a function or not a function. To determine whether a graph is a function, draw a vertical line parallel to the y-axis or perpendicular to the x- axis. If the line intersects the graph once then graph is a function. If the line intersects the graph more than once then the relation is not a function of x. Because functions are single-valued relations and a particular x-value is mapped onto one and only one y-value. Function not a function (one to many relation) TEST FOR ONE –TO– ONE FUNCTION ii. Horizontal – line test The horizontal – line test is used to determine whether a function is a one-to-one function.
    [Show full text]
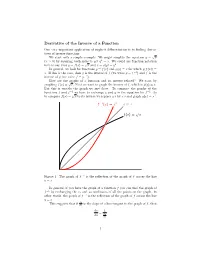
  • Derivative of the Inverse of a Function One Very Important Application of Implicit Differentiation Is to finding Deriva­ Tives of Inverse Functions
    Derivative of the Inverse of a Function One very important application of implicit differentiation is to finding deriva­ tives of inverse functions. We start with a simple example. We might simplify the equation y = px (x > 0) by squaring both sides to get y2 = x. We could use function notation here to say that y = f(x) = px and x = g(y) = y2. In general, we look for functions y = f(x) and g(y) = x for which g(f(x)) = x. If this is the case, then g is the inverse of f (we write g = f −1) and f is the inverse of g (we write f = g−1). How are the graphs of a function and its inverse related? We start by graphing f(x) = px. Next we want to graph the inverse of f, which is g(y) = x. But this is exactly the graph we just drew. To compare the graphs of the functions f and f −1 we have to exchange x and y in the equation for f −1 . So to compare f(x) = px to its inverse we replace y’s by x’s and graph g(x) = x2. 1 2 f − (x)=x y = x f(x)=√x −1 Figure 1: The graph of f is the reflection of the graph of f across the line y = x In general, if you have the graph of a function f you can find the graph of −1 f by exchanging the x- and y-coordinates of all the points on the graph.
    [Show full text]
  • Functions-Handoutnonotes.Pdf
    Introduction Functions Slides by Christopher M. Bourke You’ve already encountered functions throughout your education. Instructor: Berthe Y. Choueiry f(x, y) = x + y f(x) = x f(x) = sin x Spring 2006 Here, however, we will study functions on discrete domains and ranges. Moreover, we generalize functions to mappings. Thus, there may not always be a “nice” way of writing functions like Computer Science & Engineering 235 above. Introduction to Discrete Mathematics Sections 1.8 of Rosen [email protected] Definition Definitions Function Terminology Definition A function f from a set A to a set B is an assignment of exactly Definition one element of B to each element of A. We write f(a) = b if b is Let f : A → B and let f(a) = b. Then we use the following the unique element of B assigned by the function f to the element terminology: a ∈ A. If f is a function from A to B, we write I A is the domain of f, denoted dom(f). f : A → B I B is the codomain of f. This can be read as “f maps A to B”. I b is the image of a. I a is the preimage of b. Note the subtlety: I The range of f is the set of all images of elements of A, denoted rng(f). I Each and every element in A has a single mapping. I Each element in B may be mapped to by several elements in A or not at all. Definitions Definition I Visualization More Definitions Preimage Range Image, f(a) = b Definition f Let f1 and f2 be functions from a set A to R.
    [Show full text]
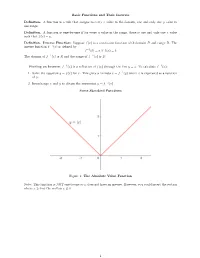
  • Basic Functions and Their Inverses Definition. a Function Is a Rule That
    Basic Functions and Their Inverses Definition. A function is a rule that assigns to every x value in the domain, one and only one y value in the range. Definition. A function is one-to-one if for every y value in the range, there is one and only one x value such that f(x) = y: Definition. Inverse Function: Suppose f(x) is a one-to-one function with domain D and range R. The inverse function f −1(x) is defined by f −1(b) = a if f(a) = b The domain of f −1(x) is R and the range of f −1(x) is D. Finding an Inverse: f −1(x) is a reflection of f(x) through the line y = x. To calculate f −1(x): 1. Solve the equation y = f(x) for x. This gives a formula x = f −1(y) where x is expressed as a function of y. 2. Interchange x and y to obtain the expression y = f −1(x) Some Standard Functions Figure 1: The Absolute Value Function Note: This function is NOT one-to-one so it does not have an inverse. However, you could invert the section where x ≥ 0 or the section x ≤ 0 1 Some Standard Functions and Their Inverses Figure 2: The Reciprocal Function Figure 3: The Quadratic Function and its Inverse 2 Some Standard Functions and Their Inverses Figure 4: The Cubic Function and its Inverse Figure 5: The Exponential Function and the Natural Log 3 Some Standard Functions and Their Inverses Figure 6: The Sine Function and its Inverse Figure 7: The Cosine Function and its Inverse 4 Some Standard Functions and Their Inverses Figure 8: The Tangent Function and its Inverse Figure 9: The Cotangent Function and its Inverse 5 Some Standard Functions and Their Inverses Figure 10: The Secant Function and its Inverse Figure 11: The Cosecant Function and its Inverse 6.
    [Show full text]
  • Chapter 14 the Inverse Function Theorem
    Chapter 14 The Inverse Function Theorem 14.1 The Intermediate Value Property 14.1 Assumption (Intermediate value property 1.) Let a, b be real numbers with a < b, and let f be a continuous function from [a, b] to R such that f(a) < 0 and f(b) > 0. Then there is some number c ∈ (a, b) such that f(c) = 0. (b,f(b)) (c,f(c)) (a,f(a)) The intermediate value theorem was first proved in 1817 by Bernard Bolzano (1781–1848). However Bolzano published his proof in a rather obscure Bo- hemian journal, and his work did not become well known until much later. Before the nineteenth century the theorem was often assumed implicitly, i.e. it was used without stating that it was an assumption. 287 288 CHAPTER 14. THE INVERSE FUNCTION THEOREM 14.2 Definition (c is between a and b.) Let a, b and c be real numbers with a 6= b. We say that c is between a and b if either a < c < b or b < c < a. 14.3 Corollary (Intermediate value property 2.) Let f be a continuous function from some interval [a, b] to R, such that f(a) and f(b) have opposite signs. Then there is some number c between a and b such that f(c) = 0. Proof: If f(a) < 0 < f(b) the result follows from assumption 14.1. Suppose that f(b) < 0 < f(a). Let g(x) = −f(x) for all x ∈ [a, b]. then g is a continuous function on [a, b] and g(a) < 0 < g(b).
    [Show full text]
  • Explicit Construction of the Inverse of an Analytic Real Function: Some Applications
    mathematics Article Explicit Construction of the Inverse of an Analytic Real Function: Some Applications Joaquín Moreno 1, Miguel A. López 2,* and Raquel Martínez 2 1 Department of Applied Mathematics, Superior Technical School of Building Engineering, Polytechnic University of Valencia, 46022 Valencia, Spain; jmfl[email protected] 2 SIDIS Research Group, Department of Mathematics and Institute of Applied Mathematics in Science and Engineering (IMACI), Polytechnic School of Cuenca, University of Castilla-La Mancha, 16071 Cuenca, Spain; [email protected] * Correspondence: [email protected] Received: 12 October 2020; Accepted: 27 November 2020; Published: 3 December 2020 Abstract: In this paper, we introduce a general procedure to construct the Taylor series development of the inverse of an analytical function; in other words, given y = f (x), we provide the power series that defines its inverse x = h f (y). We apply the obtained results to solve nonlinear equations in an analytic way, and generalize Catalan and Fuss–Catalan numbers. Keywords: inverse functions; Taylor series; Taylor Remainder; nonlinear equations; Catalan numbers; Fuss–Catalan numbers MSC: 40E99; 26A99; 30B10; 05C90 1. Introduction In this paper, we have taken as a basis the previous works [1,2], in which the inverse of a polynomial function is constructed, with the aim of generalizing the methods developed there to any analytic function. That is to say: given an analytic function around the point x0: ¥ (p) f (x0) p f (x) = f (x0) + ∑ (x − x0) p=1 p! where f (p)(x) is the p-th derivative of f (x), throughout these lines, we construction the function, x = h f (y), with y = f (x) and, therefore, x0 = h f (y0) and y0 = f (x0), such that: (p) ¥ h (y ) f 0 p h f (y) = h f (y0) + ∑ (y − y0) (1) p=1 p! To accomplish this task we have organized this article as follows: • In Section2, background theory is presented.
    [Show full text]