DOCSLIB.ORG

Equation of State for Supercooled Water at Pressures up to 400 Mpa

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Equation of State for Supercooled Water at Pressures up to 400 Mpa Equation of state for supercooled water at pressures up to 400 MPa Vincent Holten, Jan V. Sengers, and Mikhail A. Anisimova) Institute for Physical Science and Technology and Department of Chemical and Biomolecular Engineering, University of Maryland, College Park, Maryland 20742, USA (Dated: 9 September 2014) An equation of state is presented for the thermodynamic properties of cold and supercooled water. It is valid for temperatures from the homogeneous ice nucleation temperature up to 300 K and for pressures up to 400 MPa, and can be extrapolated up to 1000 MPa. The equation of state is compared with experimental data for the density, expansion coefficient, isothermal compressibility, speed of sound, and heat capacity. Estimates for the accuracy of the equation are given. The melting curve of ice I is calculated from the phase-equilibrium condition between the proposed equation and an existing equation of state for ice I. Key words: compressibility; density; equation of state; expansivity; heat capacity; speed of sound; supercooled water; thermodynamic properties Contents C. Tables 21 1. Introduction 1 References 21 2. Experimental Data 2 2.1. Density2 2.2. Density derivatives2 1. Introduction 2.3. Speed of sound2 2.4. Heat capacity4 Supercooled water has been of interest to science since it was 1 2.5. Values from IAPWS-955 first described by Fahrenheit in 1724. At atmospheric pres- 2.6. Adjustment of data5 sure, water can exist as a metastable liquid down to 235 K, 2.7. Values for extrapolation6 and supercooled water has been observed in clouds down to this temperature.2,3 Properties of supercooled water are 3. Equation of State 7 important for meteorological and climate models4,5 and for 3.1. Structure of the equation7 cryobiology.6,7 Furthermore, the thermodynamic properties of 3.2. Optimization method9 cold and supercooled water at high pressure are needed for the design of food processing.8 4. Comparison with Experimental Data 10 It is well known that several properties of supercooled wa- 4.1. Density 10 ter – such as the isobaric heat capacity, the expansion coeffi- 4.2. Expansivity 11 cient, and the isothermal compressibility – show anomalous 4.3. Isothermal compressibility 13 behavior; they increase or decrease rapidly with cooling. A 4.4. Speed of sound 14 liquid–liquid phase transition, terminated by a critical point, 4.5. Heat capacity 15 hidden below the homogeneous ice nucleation temperature 4.6. Extrapolation to 1000 MPa 15 has been proposed to explain this anomalous thermodynamic 4.7. Connection to IAPWS-95 16 behavior.9,10 4.8. Uncertainty estimates 17 Several equations of state for supercooled water have been 4.9. Ice I melting curve 17 published. Sato11 proposed an equation of state for water in 4.10. Vapor pressure 19 the liquid phase including the metastable state, valid up to 100 MPa. Jeffery and Austin12,13 developed an analytic equa- 5. Conclusion 19 tion of state of H2O that also covers the supercooled region. arXiv:1403.6777v2 [cond-mat.stat-mech] 8 Sep 2014 Kiselev and Ely14 made an early attempt to describe super- Acknowledgments 20 cooled water in terms of an equation of state incorporating critical behavior. Anisimov and coworkers15–18 also based A. Homogeneous Nucleation Curve 20 their equations of state on an assumed liquid–liquid critical B. Derivatives 20 point. Since the publication of these equations, new experi- mental data have become available that enable development of an equation of state with a significantly improved accuracy. The equation of state of this work was developed with the a)Author to whom correspondence should be addressed; electronic mail: following aims: [email protected] 1. It should represent the experimental data of liquid water 2 in the metastable region as well as possible. This work only al.,35 Asada et al.,37 and Kell and Whalley.30 To enable ex- considers supercooled water above the homogeneous nucle- trapolation of the equation above 400 MPa, density data from ation temperature. The equation does not cover the glassy state Grindley and Lind28 up to 800 MPa were included in the fit. of water (below 136 K at atmospheric pressure19). 2. The current reference for the thermodynamic properties 2.2. Density derivatives of water is the IAPWS-95 formulation.20,21 IAPWS-95 is, strictly speaking, valid only at temperatures above the melt- Several data sets exist for temperature and pressure deriva- ing curve. When extrapolated into the supercooled region, tives of the density r. The cubic expansion coefficient aP, IAPWS-95 also yields a good description of the data in the also known as expansivity, is defined as supercooled region that were available at the time the formu- lation was developed. For practical use, a new formulation for 1 ¶r aP = − ; (1) the thermodynamic properties of supercooled water should r ¶T smoothly connect with the IAPWS-95 formulation at higher P temperatures without significant discontinuities at the point of where T is the temperature and P is the pressure. The isother- switching. mal compressibility kT is defined as 3. The correlation should allow extrapolation up to 1000 MPa. There are only a few data in the supercooled region 1 ¶r = : (2) above 400 MPa, but smooth extrapolation up to 1000 MPa kT r ¶P T would be desirable. The data sets listed in Table2 were all included in the fit, with the exception of the compressibility data of Mishima.38 Mishima’s data were not included because they may be af- 2. Experimental Data fected by systematic errors of unknown size at low temper- atures. In previous work,17,18 expansivities reported by Hare Most of the experimental data that were considered in this and Sorensen34 were included in the fit. However, Hare and work have been reviewed before.17,20,22–25 In this section, we Sorensen did not measure the expansivity directly, but derived mainly discuss new data and data that were treated differently it from a fit to their density data. Because we already included than in our previous work.17,18,26 Hare and Sorensen’s density data in our fit, their expansiv- ity data were not used in the fit. Expansivity values from Ter Minassian et al.44 were calculated from their empirical corre- 2.1. Density lation. The accuracy of their correlation is not given; the rela- The experimental density data that were considered in this tive difference with expansivities calculated from IAPWS-95 work are listed in Table1 and shown in Fig.1(a). Additional is at most 3.2% in the range of 300 K to 380 K and 0 MPa to references to older data can be found in the articles of Tekácˇ 400 MPa. et al.50 and Wagner and Pruß.20 In a large part of the su- At points in the phase diagram where the expansivity is percooled region, the only available density data are those of zero, the density has a maximum with respect to temperature. Mishima.38 As a result, it is difficult to estimate the system- The temperature at which this occurs is usually referred to 45 atic error of these data at low temperatures. In a graph in his as the temperature of maximum density (TMD). Caldwell article,38 Mishima showed the random (type A) uncertainty measured the TMD for pressures up to 38 MPa, and these for each data point, which is 0.2% on average and at most measurements were included in the expansivity data set of the 0.5%. The systematic (type B) uncertainty can only be esti- fit as aP = 0 points. The recent TMD measurements of Hiro 51 mated above 253 K, in the region of overlap with density data et al. were not used, because they deviate systematically by of Kell and Whalley,30 Sotani et al.,35 and Asada et al.37 In about 1.5 K from more accurate data. this region, the densities of Mishima deviate systematically by up to 0.4% from these other data. Below 253 K, the systematic 2.3. Speed of sound uncertainty is unknown. As in earlier work,17 we adjusted the density values of Mishima, under the assumption that the sys- The experimental data on the speed of sound considered in tematic deviation at low temperatures, where it is not known, this article are given in Table3 and shown in Fig.2. Recent is the same as at higher temperatures, where it can be calcu- data that were not considered in previous work are the accu- lated. It was found that the adjusted data of Mishima do not rate measurements of the speed of sound by Lin and Trusler52 completely agree with the expansivity measurements of Ter down to of 253 K and from 1 MPa to 400 MPa. Although there Minassian et al.,44 which we consider to be more accurate. are few data points in the supercooled region, the accuracy Therefore, the adjusted data of Mishima were included in the of 0.03%–0.04% makes this an important data set. Lin and fit of the equation of state with a relatively low weight. Trusler also derived densities and isobaric heat capacities by The only experimental density data at atmospheric pressure integrating their speed-of-sound data. We have not considered that were included in the fit are those of Hare and Sorensen,34 these derived properties in the development of the equation of which are considered to be the best available. For pressures state in this work for the following reason. To enable integra- higher than atmospheric, we included data from Sotani et tion of the speed of sound, Lin and Trusler represented their 3 400 300 ) a P M ( e r u 200 s s e r P 100 (a) (b) 0 180 200 220 240 260 280 300 180 200 220 240 260 280 300 Temperature (K) Temperature (K) Adams (1931) Hare and Sorensen (1987) Speedy and Angell (1976) Ter Minassian et al.
Load more

Recommended publications
  • Physics, Chapter 17: the Phases of Matter
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Robert Katz Publications Research Papers in Physics and Astronomy 1-1958 Physics, Chapter 17: The Phases of Matter Henry Semat City College of New York Robert Katz University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/physicskatz Part of the Physics Commons Semat, Henry and Katz, Robert, "Physics, Chapter 17: The Phases of Matter" (1958). Robert Katz Publications. 165. https://digitalcommons.unl.edu/physicskatz/165 This Article is brought to you for free and open access by the Research Papers in Physics and Astronomy at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Robert Katz Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. 17 The Phases of Matter 17-1 Phases of a Substance A substance which has a definite chemical composition can exist in one or more phases, such as the vapor phase, the liquid phase, or the solid phase. When two or more such phases are in equilibrium at any given temperature and pressure, there are always surfaces of separation between the two phases. In the solid phase a pure substance generally exhibits a well-defined crystal structure in which the atoms or molecules of the substance are arranged in a repetitive lattice. Many substances are known to exist in several different solid phases at different conditions of temperature and pressure. These solid phases differ in their crystal structure. Thus ice is known to have six different solid phases, while sulphur has four different solid phases.
    [Show full text]
  • Problem Set #10 Assigned November 8, 2013 – Due Friday, November 15, 2013 Please Show All Work for Credit
    Problem Set #10 Assigned November 8, 2013 – Due Friday, November 15, 2013 Please show all work for credit To Hand in 1. 1 2. –1 A least squares fit of ln P versus 1/T gives the result Hvaporization = 25.28 kJ mol . 3. Assuming constant pressure and temperature, and that the surface area of the protein is reduced by 25% due to the hydrophobic interaction: 2 G 0.25 N A 4 r Convert to per mole, ↓determine size per molecule 4 r 3 V M N 0.73mL/ g 60000g / mol (6.02 1023) 3 2 2 A r 2.52 109 m 2 23 9 2 G 0.25 N A 4 r 0.0720N / m 0.25 6.02 10 / mol (4 ) (2.52 10 m) 865kJ / mol We think this is a reasonable approach, but the value seems high 2 4. The vapor pressure of an unknown solid is approximately given by ln(P/Torr) = 22.413 – 2035(K/T), and the vapor pressure of the liquid phase of the same substance is approximately given by ln(P/Torr) = 18.352 – 1736(K/T). a. Calculate Hvaporization and Hsublimation. b. Calculate Hfusion. c. Calculate the triple point temperature and pressure. a) Calculate Hvaporization and Hsublimation. From Equation (8.16) dPln H sublimation dT RT 2 dln P d ln P dT d ln P H T 2 sublimation 11 dT dT R dd TT For this specific case H sublimation 2035 H 16.92 103 J mol –1 R sublimation Following the same proedure as above, H vaporization 1736 H 14.43 103 J mol –1 R vaporization b.
    [Show full text]
  • Phase Diagrams a Phase Diagram Is Used to Show the Relationship Between Temperature, Pressure and State of Matter
    Phase Diagrams A phase diagram is used to show the relationship between temperature, pressure and state of matter. Before moving ahead, let us review some vocabulary and particle diagrams. States of Matter Solid: rigid, has definite volume and definite shape Liquid: flows, has definite volume, but takes the shape of the container Gas: flows, no definite volume or shape, shape and volume are determined by container Plasma: atoms are separated into nuclei (neutrons and protons) and electrons, no definite volume or shape Changes of States of Matter Freezing start as a liquid, end as a solid, slowing particle motion, forming more intermolecular bonds Melting start as a solid, end as a liquid, increasing particle motion, break some intermolecular bonds Condensation start as a gas, end as a liquid, decreasing particle motion, form intermolecular bonds Evaporation/Boiling/Vaporization start as a liquid, end as a gas, increasing particle motion, break intermolecular bonds Sublimation Starts as a solid, ends as a gas, increases particle speed, breaks intermolecular bonds Deposition Starts as a gas, ends as a solid, decreases particle speed, forms intermolecular bonds http://phet.colorado.edu/en/simulation/states- of-matter The flat sections on the graph are the points where a phase change is occurring. Both states of matter are present at the same time. In the flat sections, heat is being removed by the formation of intermolecular bonds. The flat points are phase changes. The heat added to the system are being used to break intermolecular bonds. PHASE DIAGRAMS Phase diagrams are used to show when a specific substance will change its state of matter (alignment of particles and distance between particles).
    [Show full text]
  • CH 222 Oregon State University Week 6 Worksheet Notes
    CH 222 Oregon State University Week 6 Worksheet Notes 1. Place the following compounds in order of decreasing strength of intermolecular forces. HF O2 CO2 HF > CO2 > O2 2. In liquid propanol, CH3CH2CH2OH, which intermolecular forces are present? Dispersion, hydrogen bonding and dipole-dipole forces are present. 3. Assign the appropriate labels to the phase diagram shown below. A) A = liquid, B = solid, C = gas, D = critical point B) A = gas, B = solid, C = liquid, D = triple point C) A = gas, B = liquid, C = solid, D = critical point D) A = solid, B = gas, C = liquid, D = supercritical fluid E) A = liquid, B = gas, C = solid, D = triple point 4. Consider the phase diagram below. If the dashed line at 1 atm of pressure is followed from 100 to 500°C, what phase changes will occur (in order of increasing temperature)? A) condensation, followed by vaporization B) sublimation, followed by deposition C) vaporization, followed by deposition D) fusion (melting), followed by vaporization E) No phase change will occur under the conditions specified. 5. Which of the following solutions will have the highest concentration of chloride ions? A) 0.10 M NaCl B) 0.10 M MgCl2 C) 0.10 M AlCl3 D) 0.05 M CaCl2 E) All of these solutions have the same concentration of chloride ions. 6. Commercial grade HCl solutions are typically 39.0% (by mass) HCl in water. Determine the molarity of the HCl, if the solution has a density of 1.20 g/mL. A) 7.79 M B) 10.7 M C) 12.8 M D) 9.35 M E) 13.9 M 7.
    [Show full text]
  • Triple Point
    AccessScience from McGraw-Hill Education Page 1 of 2 www.accessscience.com Triple point Contributed by: Robert L. Scott Publication year: 2014 A particular temperature and pressure at which three different phases of one substance can coexist in equilibrium. In common usage these three phases are normally solid, liquid, and gas, although triple points can also occur with two solid phases and one liquid phase, with two solid phases and one gas phase, or with three solid phases. According to the Gibbs phase rule, a three-phase situation in a one-component system has no degrees of freedom (that is, it is invariant). Consequently, a triple point occurs at a unique temperature and pressure, because any change in either variable will result in the disappearance of at least one of the three phases. See also: PHASE EQUILIBRIUM . Triple points are shown in the illustration of part of the phase diagram for water. Point A is the well-known ◦ triple point for Ice I (the ordinary low-pressure solid form) + liquid + water + water vapor at 0.01 C (273.16 K) and a pressure of 0.00603 atm (4.58 mmHg or 611 pascals). In 1954 the thermodynamic temperature scale (the absolute or Kelvin scale) was redefined by setting this triple-point temperature for water equal to exactly 273.16 K. Thus, the kelvin (K), the unit of thermodynamic temperature, is defined to be 1 ∕ 273.16 of the thermodynamic temperature of this triple point. ◦ Point B , at 251.1 K ( − 7.6 F) and 2047 atm (207.4 megapascals) pressure, is the triple point for liquid water + Ice ◦ I + Ice III; and point C , at 238.4 K ( − 31 F) and 2100 atm (212.8 MPa) pressure, is the triple point for Ice I + Ice II + Ice III.
    [Show full text]
  • Superconductivity for Accelerators
    Superconductivity for accelerators - why bother? Abolish Ohm's • no power consumption Law(although do need refrigeration power) • high current density ⇒ compact windings, high gradients • ampere turns are cheap, so don’t need iron ⇒ high fields (although often use it for shielding) Consequence • lower power bills s • higher magnetic fields mean reduced bend radius ⇒ smaller rings ⇒ reduced capital cost ⇒ new technical possibilities (eg muon collider) • higher quadrupole gradients ⇒ higher luminosity Martin Wilson Lecture 1 slide 1 JUAS February 2015 Superconducting Magnets: plan of the lectures 1 Introduction to Superconductors 4 Quenching and Protection • critical field, temperature & current • the quench process • superconductors for magnets • resistance growth, current decay, • manufacture of superconducting wires temperature rise • high temperature superconductors HTS • calculating the quench • where to find more • mini tutorial 2 Magnetization, Cables & AC losses • quench protection schemes • superconductors in changing fields, critical state model • filamentary superconductors and magnetization 5 Cryogenics & Practical Matters • coupling between filaments ⇒ magnetization • working fluids, refrigeration • why cables, coupling in cables • cryostat design • mini tutorial • current leads • AC losses in changing fields • accelerator magnet manufacture 3 Magnets, ‘Training’ & Fine Filaments • some superconducting accelerators • coil shapes for solenoids, dipoles & quadrupoles • engineering current density & load lines mini tutorials •
    [Show full text]
  • Thermodynamic Curvature from the Critical Point to the Triple Point
    Thermodynamic curvature from the critical point to the triple point George Ruppeiner∗ Division of Natural Sciences New College of Florida 5800 Bay Shore Road Sarasota, Florida 34243-2109 October 30, 2018 Abstract I evaluate the thermodynamic curvature R for fourteen pure fluids along their liquid-vapor coexistence curves, from the critical point to the triple point, using thermodynamic input from the NIST Chem- istry WebBook. In this broad overview, R is evaluated in both the coexisting liquid and vapor phases. R is an invariant whose magni- tude jRj is a measure of the size of mesoscopic organized structures in a fluid, and whose sign specifies whether intermolecular interactions are effectively attractive (R < 0) or repulsive (R > 0). I discuss five principles for R in pure fluids: 1) near the critical point, the attractive part of the interactions forms loose structures of size jRj proportional to the correlation volume ξ3, and sign of R negative, 2) in the vapor phase, there are instances of compact clusters of size jRj formed by the attractive part of the interactions and prevented from collapse by the repulsive part of the interactions, and sign of R positive, 3) in the asymptotic critical point regime, the R's in the coexisting liquid and arXiv:1208.3265v1 [cond-mat.stat-mech] 16 Aug 2012 vapor phases are equal to each other, i.e., commensurate, 4) outside the asymptotic critical point regime incommensurate R's may be as- sociated with metastability, and 5) the compact liquid phase has jRj ∗[email protected] 1 on the order of the volume of a molecule, with sign of R negative for a liquidlike state held together by attractive interactions and sign of R positive for a solidlike state held up by repulsive interactions.
    [Show full text]
  • Triple Point of Water
    Demonstration 4 Latent Heat of Vaporization The Triple Point of Water gas phase liquid + gas liquid phase solid + liquid solid phase Temperature Time When a liquid is boiling, molecules are constantly leaving the surface and in the process changing from a liquid state to a gas state. As each molecule leaves the surface it will take some thermal energy with it. The amount of thermal energy will be determined by the heat required to reach the boiling point of the liquid plus the latent heat of vaporization defined as “the quantity of heat required to change unit mass of liquid into vapor at the boiling point”. Normally, the thermal energy necessary to reach and sustain boiling is supplied to the liquid from an external source. If instead, the liquid is made to boil by reducing the pressure over the surface with no external heat provided, the process is reversed. The molecules leaving the liquid surface and entering the gas state still require their latent heat as before; but, since no heat is being supplied, the thermal energy is obtained from the molecules that remain in the liquid state. This will result in a reduction in the kinetic energy of the remaining molecules of liquid. The loss of kinetic energy will cause a drop in the temperature of the remaining liquid. If enough cooling occurs, the liquid will undergo yet another phase change to a solid. When all three phases are present and in equilibrium, the temperature and pressure condi- tions at which this occurs is called the “triple point”. Once the triple-point is reached, additional pumping will remove the gas phase and the solid phase (ice in the case of water) will remain.
    [Show full text]
  • Pressure-Induced Superconductivity in the Three-Component Fermion
    Pressure-induced Superconductivity in the Three-component Fermion Topological Semimetal Molybdenum Phosphide Zhenhua Chi1, Xuliang Chen2, Chao An2,3, Liuxiang Yang4, Jinggeng Zhao5,6, Zili Feng7,8, Yonghui Zhou2, Ying Zhou2,3, Chuanchuan Gu2, Bowen Zhang2,3, Yifang Yua n 2,9, Curtis Kenney-Benson10, Wenge Yang 11, Gang Wu12, Xiangang Wan13,14, Youguo Shi7,¦, Xiaoping Yang2,＄, Zhaorong Yang2,14,§ 1Key Laboratory of Materials Physics, Institute of Solid State Physics, Chinese Academy of Sciences, Hefei 230031, China 2Anhui Province Key Laboratory of Condensed Matter Physics at Extreme Conditions, High Magnetic Field Laboratory, Chinese Academy of Sciences, Hefei 230031, China 3University of Science and Technology of China, Hefei 230026, China 4Center for High Pressure Science and Technology Advanced Research (HPSTAR), Beijing 100094, China 5Department of Physics, Harbin Institute of Technology, Harbin 150080, China 6Natural Science Research Center, Academy of Fundamental and Interdisciplinary Sciences, Harbin Institute of Technology, Harbin 150080, China 7Beijing National Laboratory for Condensed Matter Physics and Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China 8School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100190, China 9Department of Physics and Engineering, Zhengzhou University, Zhengzhou 450052, China 10HPCAT, Geophysical Laboratory, Carnegie Institution of Washington, Argonne, Illinois 60439, USA 11Center for High Pressure Science and Technology Advanced Research (HPSTAR),
    [Show full text]
  • Physical Chemistry Icarnot Cycle
    Lecture 17 Chapter 9, sections 1-3 Announce: • Remember to complete and return Dr. Krueger’s mid-term evaluations forms • Chem seminar on Friday Outline: Phase Transitions ∂G = −S ∂ T p Phase Diagrams (H2O and CO2) ∂G = V ∂ p T Chemical Potential ∂G µ = ∂ n p,T Review: Some protein and nucleic acid binding events are driven by enthalpy and some by entropy. The balance between the two is governed by the solvent interactions: favorable solvent interactions Æ enthalpy controlled poor solvent interactions Æ entropy controlled The body makes nonspontaneous reactions happen by coupling them to exergonic reactions like ATP Æ ADP Phase Diagrams Phase Diagrams Summarize Solid-Liquid-Gas Behavior of a Substance Let’s start by defining a phase: form of matter that is uniform throughout in chemical composition and physical state. phase transition: the spontaneous conversion of one phase to another that occurs at a well-defined temperature – the transition temperature said another way, the transition temperature is the temperature at which the Gibbs free energies for both phases are? equal (remember that the system is seeking the minimum Gibbs free energy). 1 We can explain transition temperatures by understanding how the Gibbs energy changes with temperature: Recall that G is a function of p and T, so then the total derivative is? ∂G ∂G dG = dp + dT (from definition of total derivative for dG) ∂p ∂T T p But, we also know from our fundamental equation for G?: dG = Vdp - SdT As we have done three times before, you guys can quickly fill in? ∂G ∂G = Vand =−S (equating coefficients in expressions for dG) ∂p ∂T T p Therefore, if we plot G vs.
    [Show full text]
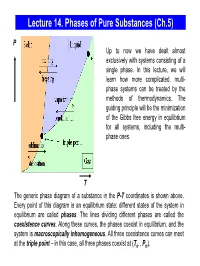
  • Lecture 14. Equilibrium Between Phases
    Lecture 14. Phases of Pure Substances (Ch.5) P Up to now we have dealt almost exclusively with systems consisting of a single phase. In this lecture, we will learn how more complicated, multi- phase systems can be treated by the methods of thermodynamics. The guiding principle will be the minimization of the Gibbs free energy in equilibrium for all systems, including the multi- phase ones. T The generic phase diagram of a substance in the P-T coordinates is shown above. Every point of this diagram is an equilibrium state; different states of the system in equilibrium are called phases. The lines dividing different phases are called the coexistence curves. Along these curves, the phases coexist in equilibrium, and the system is macroscopically inhomogeneous. All three coexistence curves can meet at the triple point – in this case, all three phases coexist at (Ttr , Ptr). The Coexistence Curves Along the coexistence curves, two different phases 1 and 2 coexist in equilibrium (e.g., ice and water coexist at T = 00C and P = 1bar). The system undergoes phase separation each time we cross the equilibrium curve (the system is spatially inhomogeneous along the equilibrium curves). Any system in contact with the thermal bath is governed by the minimum free energy principle. The shape of coexistence curves on the P-T phase diagram is determined by the condition: GPTGPT,,= and, since 1()2 ( ) GN= μ PTPTμ1( ,,) = μ2 ( ) - otherwise, the system would be able to decrease its Gibbs free energy by transforming the phase with a higher μ into the phase with lower μ.
    [Show full text]
  • Make a Triple Point Apparatus Student Laboratory SCIENTIFIC
    Make a Triple Point Apparatus Student Laboratory SCIENTIFIC Introduction View carbon dioxide in the solid, liquid, and gas forms simultaneously using a simple triple point apparatus made by you right in the laboratory! Concepts • Sublimation • Phase diagrams • Triple point Background We have all observed what occurs when dry ice (solid state of carbon dioxide, 72.8 CO2) is removed from a freezer. As the temperature on the surface of the dry Solid Liquid ice increases above –78 °C, the solid changes directly to a vapor bypassing the liquid phase. This spontaneous change from a solid to a gas is called sublimation. Sublimation of CO2 occurs when the temperature is above –78 °C at a pressure of 1 atm, standard atmospheric pressure. Standard 67 pressure on Earth is 1 atm. Liquid CO2 is not stable under Earth’s standard pressure, and therefore does not exist under normal pressure conditions. Refer 5.1 to the phase diagram, Figure 1. Pressure (atm) A phase diagram has temperature as the independent (x) and pressure as the 1 Gas dependent (y) axis. According to the phase diagram that the liquid phase of CO 2 –78 –56 25 31 is stable only under a pressure of 5.2 atm or higher, at a temperature above Temperature ( C) –57 °C. The junction where the gas, liquid, and solid phases all exist in ϒ equilibrium is called the triple point. When a substance is at the triple point, all Figure 1. Phase diagram of carbon three phases are present simultaneously. dioxide. The terms melting point (solid to liquid) and boiling point (liquid to gas) are often used when discussing phase changes.
    [Show full text]