DOCSLIB.ORG

Scenarios of Urban Growth in Kenya Using Regionalised Cellular Automata Based on Multi Temporal Landsat Satellite Data

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Scenarios of Urban Growth in Kenya Using Regionalised Cellular Automata Based on Multi Temporal Landsat Satellite Data Scenarios of Urban Growth in Kenya Using Regionalised Cellular Automata based on Multi temporal Landsat Satellite Data Dissertation Zur Erlangung des Doktorgrades (Dr. rer. nat.) der Mathematisch-Naturwissenschaftlichen Fakultät der Rheinischen Friedrich-Wilhelms-Universität Bonn Vorgelegt von Kenneth Wagia MUBEA Aus Nairobi, Kenia Bonn, 2014 Angefertigt mit Genehmigung der Mathematisch-Naturwissenschaftlichen Fakultät der Rheinischen Friedrich-Wilhelms-Universität Bonn 1. Referent: Prof. Dr. Gunter Menz 2. Referent: Prof. Dr. Klaus Greve Tag der Promotion: 15 April 2014 Erscheinungsjahr: 2014 Diese Dissertation ist auf dem Hochschulschriftenserver der ULB Bonn http://hss.ulb.uni-bonn.de/diss_online elektronisch publiziert ii TABLE OF CONTENTS ACKNOWLEDGEMENTS ................................................................................................... VI ABSTRACT ...................................................................................................................... VIII ZUSAMMENFASSUNG ....................................................................................................... X ACRONYMS ...................................................................................................................... XII LIST OF FIGURES ............................................................................................................. XIII LIST OF TABLES ............................................................................................................... XV LIST OF PAPERS .............................................................................................................. XVI 1 INTRODUCTION .................................................................................................. 1 1.1 Purpose of the Research .................................................................................... 1 1.2 Statement of the problem ................................................................................. 4 1.3 Research Questions ............................................................................................ 5 1.4 Research objectives ............................................................................................ 5 1.5 Outline of the research ...................................................................................... 6 2 URBAN GROWTH MODELLING AND CELLULAR AUTOMATA ............................. 9 2.1 Introduction........................................................................................................ 9 2.2 Urban modelling ............................................................................................... 10 2.2.1 Models .............................................................................................................. 10 2.2.2 Types of Models ............................................................................................... 11 2.2.3 Challenges ........................................................................................................ 12 2.2.4 Model uncertainty ............................................................................................ 15 2.3 Modelling urban growth .................................................................................. 18 2.3.1 Background ....................................................................................................... 18 2.3.2 Modelling approaches ...................................................................................... 19 2.3.3 Current practices in urban land-use modelling ................................................ 22 2.3.4 Complexity of Urban Growth ........................................................................... 24 2.3.5 Role of GIS and remote sensing in urban growth modelling ........................... 26 2.4 Cellular automata modelling ............................................................................ 28 2.4.1 Introduction...................................................................................................... 28 2.4.2 Elements of Cellular Automata ........................................................................ 30 2.4.3 Cellular automata models ................................................................................ 34 2.4.4 Advantages of CA urban models ...................................................................... 38 2.4.5 Limitations of CA urban models ....................................................................... 38 2.4.6 Developments in CA models ............................................................................ 39 2.4.7 Cellular automata in urban growth modelling ................................................. 41 iii 3 URBAN GROWTH IN AFRICAN CITIES ............................................................... 43 3.1 Introduction...................................................................................................... 43 3.2 Sustainable growth and characteristics of African cities ................................. 45 3.3 Prosperity of cities ............................................................................................ 47 3.4 Factors influencing urban growth .................................................................... 49 3.5 Nairobi .............................................................................................................. 51 3.5.1 Research area ................................................................................................... 51 3.5.2 Background ....................................................................................................... 53 3.5.3 Physical characteristics..................................................................................... 55 3.5.4 Urban growth in Nairobi .................................................................................. 56 3.6 Nakuru .............................................................................................................. 58 3.6.1 Research area ................................................................................................... 58 3.6.2 Background ....................................................................................................... 59 3.6.3 Physical characteristics..................................................................................... 62 3.6.4 Urban growth in Nakuru .................................................................................. 63 4 MONITORING LAND-USE CHANGES ................................................................. 64 4.1 Introduction...................................................................................................... 64 4.2 Utility of multi-sensor satellite data ................................................................ 66 4.3 Land-use change analysis in Nakuru ................................................................ 70 4.3.1 Data .................................................................................................................. 70 4.3.2 Land-use classification ..................................................................................... 71 4.3.3 Results and Discussion ..................................................................................... 75 4.3.4 Factors influencing land-use changes and urban growth ................................ 86 4.3.5 Consequences of Nakuru’s urban growth ........................................................ 89 4.4 Land-use change analysis in Nairobi ................................................................ 90 4.4.1 Data .................................................................................................................. 90 4.4.2 Land-use classification ..................................................................................... 91 4.4.3 Results and discussion ...................................................................................... 92 4.4.4 Factors influencing land-use changes and urban growth ................................ 95 4.4.5 Consequences of Nairobi’s urban growth ........................................................ 98 5 MODELLING URBAN GROWTH ....................................................................... 100 5.1 Introduction.................................................................................................... 100 5.2 The modelling framework (XULU) .................................................................. 103 5.3 Model Parameters and Growth Types ........................................................... 105 5.4 Model calibration ........................................................................................... 109 5.5 Model validation ............................................................................................ 109 5.6 Scenarios of urban growth ............................................................................. 112 iv 5.7 Scenarios of urban growth in Nakuru ............................................................ 114 5.7.1 Data ................................................................................................................ 114 5.7.2 Modelling of urban growth in Nakuru ........................................................... 117 5.8 Scenarios of urban process in Nairobi ........................................................... 130 5.8.1 Data ................................................................................................................ 130 5.8.2 Modelling of urban growth in Nairobi ..........................................................
Load more

Recommended publications
  • Functional V. Jurisdictional Analysis of Metropolitan Areas (The Demographia City Sector Model) June 6, 2014
    Functional v. Jurisdictional Analysis of Metropolitan Areas (The Demographia City Sector Model) June 6, 2014 The City Sector Model is not dependent upon municipal boundaries (the term "city" is generic, and refers to cities in their functional sense, metropolitan areas, or in their physical sense, urban areas). Not being constrained by municipal boundaries is important because core municipalities vary substantially. For example, the core municipality represents less than 10 percent of the population of Atlanta, while the core municipality represents more than 60 percent of the population of San Antonio. The City Sector Model applies data available from the US Census Bureau to estimate the population and distribution of Pre-Auto Urban Cores in a consistent manner. At the same time, the approach is materially different from the Office of Management and Budget (OMB) classification of "principal cities." It also differs from the Brookings Institution "primary cities," which is based on the OMB approach. The OMB-based classifications classify municipalities using employment data, without regard to urban form, density or other variables that are associated with the urban core. These classifications are useful and acknowledge that the monocentric nature of US metropolitan areas has evolved to polycentricity. However, non-urban-core principal cities and primary cities are themselves, with few exceptions, functionally suburban. The criteria in the City Sector Model are calibrated to the 2010 US Census and is applied to major metropolitan areas
    [Show full text]
  • Three Models of Urban Growth (Land Use)
    CHANGING CITIES: Three Models of Urban Growth (Land Use) The study of urban land use generally draws from three different descriptive models. These models were developed to generalize about the patterns of urban land use found in early industrial cities of the U.S. Because the shape and form of American cities changed over time, new models of urban land were developed to describe an urban landscape that was becoming increasingly complex and differentiated. Further, because these are general models devised to understand the overall patterns of land use, none of them can accurately describe patterns of urban land use in all cities. In fact, all of these models have been criticized for being more applicable to cities in the U.S. than to cities of other nations. Other criticisms have focused on the fact that the models are static; they describe patterns of urban land use in a generic city, but do not describe the process by which land use changes. Despite these criticisms, these models continue to be useful generalizations of the way in which land is devoted to different uses within the city. Below, we will examine the Concentric Zone Model, Sector Model and Multiple Nuclei Model of urban land use. Concentric Zone Model: The concentric zone model was among the early descriptions of urban form. Originated by Earnest Burgess in the 1920s, the concentric zone model depicts the use of urban land as a set of concentric rings with each ring devoted to a different land use (see Figure 1). The model was based on Burgess’s observations of Chicago during the early years of the 20th century.
    [Show full text]
  • Compare and Contrast the Concentric, Sector and Multiple Nuclei Models
    Name: _________________________ AP Human Geography Cities and Urban Land Use Comparing and Contrasting Urban Models In this activity you will Compare and Contrast the Concentric, Sector and Multiple nuclei models. Implicit assumptions of Burgess, Hoyt, and Harris and Ullman’s models of urban structure in common: A. Their implicit assumptions are: 1) Great variation in characteristics e.g. heterogeneity of the population in culture and society. 2) Competition for centrality because of limited space leading to highest land value. The opposite is true of peripheral areas. 3) City center being center of employment. 4) Commercial and industrial base to the economy of the city. 5) Private ownership of property and capitalist mode of competition for space. 6) Expanding area and population of the city by invasion and succession. 7) No historic survival in any district to influence the land-use pattern. 8) No districts being more attractive because of differences in terrain. 9) Hierarchical order of land use. B. The Concentric, Sector models and multiple nuclei models have many features in common: 1) Both models focus on importance of accessibility. The centrally located C.B.D. is the most accessible and its land value or rent-bid is the highest. 2) Distance decay theory is applicable in both models. Land value and population density decline with distance from the central places. 3) There are clear-cut and abrupt boundaries between the land-use zones. 4) Both concern the study of ground-floor functions instead of the three-dimensional study as height of buildings is neglected 5) Residential segregation Social-economic status segregates residential areas.
    [Show full text]
  • Homer Hoyt: Sector Model Harris and Ulman: Separate Nuclei Model Http
    Homer Hoyt: Sector Model Harris and Ulman: Separate Nuclei Model Source: adapted from H. Carter (1995) Urban Geography, Fourth Edition, London: Arnold, p. 126. Sector and Nuclei Urban Land Use Representations A study done in 1939 by Homer Hoyt concluded that the land use pattern was not a random distribution, nor sharply defined rectangular areas or concentric circles but rather sectors. Communication axes are mainly responsible for the creation of sectors, thus transport has directional effect on land uses. We can see on the sector representation that Burgess transitional process is still part of land use changes, but there exist axes along which urban activities are oriented. Following Hoyt’s development of a sectorial city, C.D. Harris and E.L. Ullman (1945) introduced a more effective generalization of urban land uses. It was brought forward that many towns and nearly all large cities do not grow from around one CBD, but are formed by the progressive integration of a number of separate nuclei in the urban pattern. These nodes become specialised and differentiated in the growth process and are not located in relation to any distance attribute, but are bound by a number of attributes: * Differential accessibility. Some activities require specialized facilities such as port and rail terminals. For instance, the retailing sector demands maximum accessibility, which is often different from centrality offered in the CBD. * Land use compatibility. Similar activities group together since proximity implies improved interactions. Service activities such as banks, insurance companies, shops and institutions are strongly interacting with each other. This can be defined as centripetal forces between activities.
    [Show full text]
  • Urban Geography AP HUMAN GEOGRAPHY – UNIT 8 (Ch.9) Urban
    Urban Geography AP HUMAN GEOGRAPHY – UNIT 8 (Ch.9) Urban The built up area in and around a city. An urban area is nonrural and nonagricultural. Urbanization The growth and diffusion of city landscapes and urban lifestyles. • Urbanized area has a min. of 50,000 people • 75% of U.S Pop. Live in urban places City • An agglomeration of people and buildings clustered together • Serve as a center of politics, culture and economics. • WHY? • Oregon's largest City? 1. Portland: 600,000 2. Eugene: 156,000 3. Salem: 154,000 The incredibly slow growth of cities People have existed for 100,000 years First cities established 8,000 years ago Reached modern size and structure in last 200 years Urbanization – By the Numbers In 1800 only 5% of the world lived in cities In 1950, only 16% lived in cities In 2017, more than 50% of the world lives in cities Urbanization – By the Numbers In More Developed countries (MDC’s) nearly 75% of the population lives in cities In Less Developed Countries (LDC’s) only 40% of the population lives in cities Numbers are changing quickly – because LDCs are urbanizing at a rate much faster than the MDCs. Urbanization – By the Numbers Africa and Asia are the least urbanized continents. North America is the most urbanized. Urbanization – By the Numbers In 1950 only 83 cities had a population over 1 million In 2000, over 400 cities over 1 million In 2016, seven of the ten most populous cites were located in Asia https://www.ted.com/talks/eduardo_paes_the_4_c ommandments_of_cities?language=en 4 Commandments of Cities (Eduardo Paes, the mayor of Rio de Janeiro) Identify and explain the FOUR commandments of what a city needs to do to prosper in the future.
    [Show full text]
  • Compare and Contrast the Concentric, Sector and Multiple Nuclei Models
    KEY Compare and contrast the Concentric, Sector and Multiple nuclei models The Concentric, Sector models and multiple nuclei models have many features in common: 1) Both models focus on importance of accessibility. The centrally located C.B.D. is the most accessible and its land value or rent-bid is the highest. 2) Distant decay theory is applicable in both models. Land value and population density decline with distance from the central places. 3) There are clear-cut and abrupt boundaries between the land-use zones. 4) Both concern the study of ground-floor functions instead of the three-dimensional study as height of buildings is neglected 5) Residential segregation Social-economic status segregates residential areas. The lower-income groups live in the inner city which is suffering from urban decay or in areas near the factory zone. Nearness to working places reduces time and cost of transport, but gives better working opportunities and easiness of obtaining various order of goods and services. In contrast, the higher- income groups occupy the urban periphery with better living environment far away from the factory zone and the lower-income groups. Their implicit assumptions are: 1) Great variation in characteristics e.g. heterogeneity of the population in culture and society. 2) Competition for centrality because of limited space leading to highest land value. The opposite is true of peripheral areas. 3) City centre being centre of employment. 4) Commercial and industrial base to the economy of the city. 5) Private ownership of property and capitalist mode of competition for space. 6) Expanding area and population of the city by invasion and succession.
    [Show full text]
  • The Development and Use of a Land-Use Suitability Model in Spatial Planning in South Africa
    The development and use of a land-use suitability model in spatial planning in South Africa D.P. Cilliers Dissertation submitted in fulfilment of the requirements for the degree Magister Artium et Scientiae (Planning) at the Potchefstroom Campus of the North-West University ..­ Supervisor: Dr J.E. Drewes May 2010 . i!a "OJ<n<.wmo".oomYUtllBESITI 'fA BOKOllE·OOPHtRIMA tIOQR.O\'/SS·UH1VERSITglT Potchefstroom ~ ExpreSSlon of thanks A special word of thanks to: • My redeemer Jesus Christ, for there is only ONE way. • My supervisor, Dr Ernst Drewes, for his guidance and inputs throughout the study. • Prof Leon van Rensburg and the School for Environmental Sciences and Development, Potchefstroom Campus, for financial and infrastructural support • Mr. Theuns de Klerk, Prof Luke Sandham and Prof Francois Retief for their valuable inputs. • My parents and siblings for their support and encouragement. • My best friend and fiancee, Charlotte for her unconditional support and understanding. - i The development and use of a land-use sultabllity model in spatial planning in South Africa Table of Contents Expression of thanks Table of contents ii List of tables -v List of figures -v Abstract - vii Opsomming viii Preface - ix - 1 1.2. Research aims and objectives - 3 1.3. Basic hypothesis/central theoretical statement 3 1.4. Format of study and research methods - 3 1.4.1. Literature study - 3 1.4.2. Article 1: A GIS-based approach for visualising urban growth - 4 1.4.3. Article 2: Land-use suitability modelling as a framework for spatial planning in Tlokwe - 4 Local Municipality, North West, South Africa -7 2.2.
    [Show full text]
  • Multiple-Nuclei Model: AP Human Geography Crash Course
    Multiple-Nuclei Model: AP Human Geography Crash Course Are you an urbanite? Whether you like it or not, you are probably one of the growing numbers of people in the United States who live either in a city or close enough to quickly travel to one. Cities are growing much faster than rural areas, and the dynamics of urban geography are an important subject to know about for the AP Human Geography exam. There are several classic models used to understand and explain the internal structures of cities and urban areas, and we are going to learn about Harris and Ullman’s Multiple-Nuclei Model in this AP Human Geography study guide. What is a City? Cities are at the center of every advanced society and act as the hub of economic, social and political activities in that area. They have a variety of shapes and functions, and their geography impacts the daily lives of those who live in the city and surrounding areas. All cities provide their residents a variety of services and functions: shopping, manufacturing, transportation, education, medical, and protective services. Cities evolved over time, and if a city had favorable factors (agriculture, access to water, trade, defense), its population increased. This led to urbanization (rapid growth, and migration to large cities). This increase in urban population resulted in rapid expansion of the city and greater urbanization of the society. After the conclusion of World War II, North America experienced rapid urbanization. There was a need for housing outside of the core urban areas due to growing population and demand.
    [Show full text]
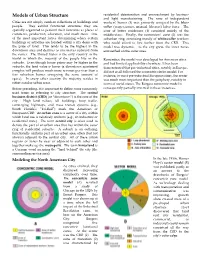
  • Models of Urban Structure Residential Deterioration and Encroachment by Business and Light Manufacturing
    Models of Urban Structure residential deterioration and encroachment by business and light manufacturing. The zone of independent Cities are not simply random collections of buildings and workers homes (3) was primarily occupied by the blue- people. They exhibit functional structure: they are collar (wage-earners, manual laborers) labor force. The spatially organized to perform their functions as places of zone of better residences (4) consisted mainly of the commerce, production, education, and much more. One middle-class. Finally, the commuters zone (5) was the of the most important forces determining where certain suburban ring, consisting mostly of white-collar workers buildings or activities are located within a city deals with who could afford to live further from the CBD. This the price of land. This tends to be the highest in the model was dynamic. As the city grew, the inner zones downtown area and declines as one moves outward from encroached on the outer ones. the center. The United States is the only country in the world in which the majority of the people live in the Remember, the model was developed for American cities suburbs. Even though house prices may be higher in the and had limited applicability elsewhere. It has been suburbs, the land value is lower (a downtown apartment demonstrated that pre-industrial cities, notably in Europe, complex will produce much more revenue per year than a did not at all followed the concentric circles model. For few suburban homes occupying the same amount of instance, in most pre-industrial European cities, the center space). In every other country the majority resides in was much more important than the periphery, notably in either rural or urban areas.
    [Show full text]
  • Theories of Urban Growth
    THEORIES OF URBAN GROWTH • Although several theories have been developed to explain the dynamics of city growth, all such theories are based upon the operation of five ecological processes of concentration, centralization, invasion and succession and observations based upon it about actual city growth in concrete situations. • However, one can hardly find a theory of an ideal pattern of urban dynamics as growth of particular city depends upon many factors, the basic one being natural location of a city .Nevertheless, one can notice a set of common principles which govern city growth everywhere • The major theories of internal structure of urban settlements have been advanced on the basis of empirical investigations conducted in the Western urban society, particularly in North America and Europe. • . Concentric zone model • Ernest Burgess is the pioneer and his theory on city dynamics which provides the base for the later theorists on the subject. The hypothesis of this theory is that cities grow and develop outwardly in concentric zones. Burgess set out to evolve a theory of dynamics but he arrived at a theory of patterns of city growth which applies to any stage stages of urban development. According to Burgess, an urban area consists of five concentric zones which represent areas of functional differentiation and expand rapidly from the Justness centre. The zones are: • (1) The loop or commercial centre • (2) The zone of transition. • (3) The zone of working class residence • (4) The residential zone of high class apartment buildings. • (5) The commuter's zone. 1. The loop or central business district or commercial centre: • 1.
    [Show full text]
  • Demographia City Sector Model Metropolitan Area Maps
    Demographia City Sector Model Metropolitan Area Maps Functional Classifications of Sectors in US Metropolitan Areas Functional Classifications Based on 2010 Census July 2014 CITY SECTOR MODEL METROPOLITAN AREA MAPS Table of Contents City Sector Model Summary 1 Structure of the City Sector Model 2 Major Metropolitan Area Maps Listing 3 Appendix 56 CITY SECTOR MODEL: SUMMARY Summary: The Demographia City Sector Model classifies the nearly 9,000 zip code tabulation areas (ZCTA's) in the 52 major metropolitan areas of the United States, using urban form, density and travel behavior characteristics and residence age. Major metropolitan areas have more than 1,000,000 residents. Classifications: There are four functional classifications, (1) the urban core, (2) earlier suburbs, (3) later suburbs and (4) exurbs (outside the urban area and all areas with fewer than 250 residents per square mile (97 per square kilometer). The urban cores have higher densities (7,500 per square mile or 2,896 per square kilometer), and substantially greater reliance on transit, walking and cycling (20 percent or more) than other parts of metropolitan areas. The urban core also includes all non-exurban ZCTA's with a median house construction date of 1945 or before (see page 2). Replicating the Pre-Auto Suburban City: The City Sector Model criteria produces geographies functionally similar to the urban cores that preceded the great automobile oriented suburbanization that developed after World War II. Exurban areas are beyond the built up urban areas. The suburban areas constitute the balance of the major metropolitan areas. Earlier suburbs include areas with a median house construction date before 1980.
    [Show full text]
  • Models of Urban Growth : Concentric Zones, Sectors, Multiple Nuclei, Explaitative, Syrn Bolic
    Models of Urban Growth : Concentric Zones, Sectors, Multiple Nuclei, Explaitative, Syrn bolic 6.1 lntroduction 6.2 Structure of Cities 6.3 Concentric Zone Model . 6.4 Sectors Model 6.5 Multiple Nuclei Model 6.6 Exploitative Model 6.7 Symbolic Approach 6.8 Conclusion 6.9 Further Reading Learning Objectives After studying this unit you should be able to: discuss the structure of cities; describe the concentric zone model of studying the structure of cities; explain the sectors model; , describe the multiple nuclei model; discuss the exploitative model; and explain the symbolic approach to the study of city. 6.1 lntroduction Under the rubric of urban ecological process and theories, you have already learnt about the processes of invasion, succession, concentration, centralisation and segregation which characterise different kinds and dimensions of cities. Here in this unit you will learn further about the different aspects of cities and their formations. As you already know, urban society is defined as a relatively larger, dense, permanent, heterogeneous settlements whose majority of inhabitants are engaged in non-agricultural occupation. The development of such urban society is very much determined by socio - cultural organisation, climate, topography and economic development. The earliest cities of the world originated near river valleys such as early civilization of lndus (Mohenjodaro, Harrappa), Tigris - Eupharates (Lagas Ur, Uruk), Nile (Memphis, Thebes) 5 7 and Hwang Ho (Chen-Chan An Yang). These early development of urban settlements evolved with changing technology and human needs. Trade and commercial activities and settled agriculture were major facilitators; even today these,factors are very much relevant in the growth of a city.
    [Show full text]