No. 32. Let G Be a Group, Let H Be a Subgroup, and Let a and B Be Elements of G Such That Ah = Bh. Then It Follows That HA−1 = Hb−1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

National Rappel Operations Guide
National Rappel Operations Guide 2019 NATIONAL RAPPEL OPERATIONS GUIDE USDA FOREST SERVICE National Rappel Operations Guide i Page Intentionally Left Blank National Rappel Operations Guide ii Table of Contents Table of Contents ..........................................................................................................................ii USDA Forest Service - National Rappel Operations Guide Approval .............................................. iv USDA Forest Service - National Rappel Operations Guide Overview ............................................... vi USDA Forest Service Helicopter Rappel Mission Statement ........................................................ viii NROG Revision Summary ............................................................................................................... x Introduction ...................................................................................................... 1—1 Administration .................................................................................................. 2—1 Rappel Position Standards ................................................................................. 2—6 Rappel and Cargo Letdown Equipment .............................................................. 4—1 Rappel and Cargo Letdown Operations .............................................................. 5—1 Rappel and Cargo Operations Emergency Procedures ........................................ 6—1 Documentation ................................................................................................ -

Outbreak of SARS-Cov-2 Infections, Including COVID-19 Vaccine
Morbidity and Mortality Weekly Report Outbreak of SARS-CoV-2 Infections, Including COVID-19 Vaccine Breakthrough Infections, Associated with Large Public Gatherings — Barnstable County, Massachusetts, July 2021 Catherine M. Brown, DVM1; Johanna Vostok, MPH1; Hillary Johnson, MHS1; Meagan Burns, MPH1; Radhika Gharpure, DVM2; Samira Sami, DrPH2; Rebecca T. Sabo, MPH2; Noemi Hall, PhD2; Anne Foreman, PhD2; Petra L. Schubert, MPH1; Glen R. Gallagher PhD1; Timelia Fink1; Lawrence C. Madoff, MD1; Stacey B. Gabriel, PhD3; Bronwyn MacInnis, PhD3; Daniel J. Park, PhD3; Katherine J. Siddle, PhD3; Vaira Harik, MS4; Deirdre Arvidson, MSN4; Taylor Brock-Fisher, MSc5; Molly Dunn, DVM5; Amanda Kearns5; A. Scott Laney, PhD2 On July 30, 2021, this report was posted as an MMWR Early Massachusetts, that attracted thousands of tourists from across Release on the MMWR website (https://www.cdc.gov/mmwr). the United States. Beginning July 10, the Massachusetts During July 2021, 469 cases of COVID-19 associated Department of Public Health (MA DPH) received reports of with multiple summer events and large public gatherings in an increase in COVID-19 cases among persons who reside in a town in Barnstable County, Massachusetts, were identified or recently visited Barnstable County, including in fully vac- among Massachusetts residents; vaccination coverage among cinated persons. Persons with COVID-19 reported attending eligible Massachusetts residents was 69%. Approximately densely packed indoor and outdoor events at venues that three quarters (346; 74%) of cases occurred in fully vac- included bars, restaurants, guest houses, and rental homes. On cinated persons (those who had completed a 2-dose course July 3, MA DPH had reported a 14-day average COVID-19 of mRNA vaccine [Pfizer-BioNTech or Moderna] or had incidence of zero cases per 100,000 persons per day in residents received a single dose of Janssen [Johnson & Johnson] vac- of the town in Barnstable County; by July 17, the 14-day cine ≥14 days before exposure). -

Alphabets, Letters and Diacritics in European Languages (As They Appear in Geography)
1 Vigleik Leira (Norway): [email protected] Alphabets, Letters and Diacritics in European Languages (as they appear in Geography) To the best of my knowledge English seems to be the only language which makes use of a "clean" Latin alphabet, i.d. there is no use of diacritics or special letters of any kind. All the other languages based on Latin letters employ, to a larger or lesser degree, some diacritics and/or some special letters. The survey below is purely literal. It has nothing to say on the pronunciation of the different letters. Information on the phonetic/phonemic values of the graphic entities must be sought elsewhere, in language specific descriptions. The 26 letters a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z may be considered the standard European alphabet. In this article the word diacritic is used with this meaning: any sign placed above, through or below a standard letter (among the 26 given above); disregarding the cases where the resulting letter (e.g. å in Norwegian) is considered an ordinary letter in the alphabet of the language where it is used. Albanian The alphabet (36 letters): a, b, c, ç, d, dh, e, ë, f, g, gj, h, i, j, k, l, ll, m, n, nj, o, p, q, r, rr, s, sh, t, th, u, v, x, xh, y, z, zh. Missing standard letter: w. Letters with diacritics: ç, ë. Sequences treated as one letter: dh, gj, ll, rr, sh, th, xh, zh. -

Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone
Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Proposal for Generation Panel for Latin Script Label Generation Ruleset for the Root Zone Table of Contents 1. General Information 2 1.1 Use of Latin Script characters in domain names 3 1.2 Target Script for the Proposed Generation Panel 4 1.2.1 Diacritics 5 1.3 Countries with significant user communities using Latin script 6 2. Proposed Initial Composition of the Panel and Relationship with Past Work or Working Groups 7 3. Work Plan 13 3.1 Suggested Timeline with Significant Milestones 13 3.2 Sources for funding travel and logistics 16 3.3 Need for ICANN provided advisors 17 4. References 17 1 Generation Panel for Latin Script Label Generation Ruleset for the Root Zone 1. General Information The Latin script1 or Roman script is a major writing system of the world today, and the most widely used in terms of number of languages and number of speakers, with circa 70% of the world’s readers and writers making use of this script2 (Wikipedia). Historically, it is derived from the Greek alphabet, as is the Cyrillic script. The Greek alphabet is in turn derived from the Phoenician alphabet which dates to the mid-11th century BC and is itself based on older scripts. This explains why Latin, Cyrillic and Greek share some letters, which may become relevant to the ruleset in the form of cross-script variants. The Latin alphabet itself originated in Italy in the 7th Century BC. The original alphabet contained 21 upper case only letters: A, B, C, D, E, F, Z, H, I, K, L, M, N, O, P, Q, R, S, T, V and X. -

Lexia Lessons Digraph Ch
® LEVEL 6 | Phonics Lexia Lessons Digraph ch Description This lesson is designed to reinforce letter-sound correspondence for the consonant digraph ch, where the two letters, c-h, represent one sound, /ch/. Knowledge of consonant digraphs will improve students’ ability to apply phonic word attack strategies for reading and spelling. TEACHER TIPS The following steps show a lesson in which students identify the sound /ch/ at the beginning of words and match the sound to the letters c-h. For students who have difficulty distinguishing the stop sound /ch/ from the continuant sound /sh/, place emphasis on the stop sound of /ch/ by repeating it while making an abrupt chopping motion with your arm: /ch/ /ch/ /ch/. PREPARATION/MATERIALS • For each student, a card or sticky note • A copy of the ch Keyword Image Card and with the digraph ch printed on it 9 pictures at the end of the lesson • Blank sticky notes Primary Standard: CCSS.ELA-Literacy.RF.1.3a - Know the spelling-sound - Know Standard: CCSS.ELA-Literacy.RF.1.3a Primary correspondences for common consonant digraphs. Warm-up Use a phonemic awareness activity to review how to isolate the initial sound /ch/. ListenasIsayawordintwoparts:/ch/op.Thefirstsoundis/ch/.Theendingsoundsareop.WhenI putthemtogether,Igetthewordchop.Whatisthefirstsoundinchop?(/ch/) Make a single chopping motion with one arm. Thesound/ch/isthesoundwehearatthebeginningofthewordchop.Let’sallsay/ch/together:/ ch//ch//ch/.I’mgoingtosayaword.Ifthewordbeginswith/ch/,chopwithyourhandlikethisand say/ch/.Iftheworddoesnotbeginwith/ch/,keepyourhanddownandmakenosound. Suggested words: chill, chest, time, jump, chain, treasure, gentle, chocolate. Direct Instruction Reading. ® Display the Keyword Image Card of the cheese with the ch on it. -

Common Equations Used in Chemistry Equation For
Common Equations Used in Chemistry m Equation for density: d= v 5 Converting ˚F to ˚C: ˚C = (˚F - 32) x 9 9 Converting ˚C to ˚F: ˚F = ˚C x 5 + 32 Converting ˚C to K: K = (˚C + 273.15) n x molar mass of element Percent composition of an element = molar mass of compound x 100% - where n = the number of moles of the element in one mole of the compound actual yield % yield = theoretical yield x 100% moles of solute molarity (M) = liters of solution Dilution of Solution: MiVi = MfV f Boyle’s law - Constant T and n: PV = k Boyle’s law - For calculating changes in pressure or volume: P1V1 = P2V 2 V Charles’ law - Constant P and n: T = k V1 V 2 Charles’ law - For calculating temperature or volume changes: = T1 T2 Avogadro’s law - Constant P and T: V = kn Ideal Gas equation: PV = nRT Calculation of changes in pressure, temperature, or volume of gas when n is constant: P1V1 P2V 2 = T1 T2 PM Calculation of density or molar mass of gas: d = RT Dalton’s law of partial pressures - for calculating partial pressures: Pi = XiPT 3RT 0.5 Root-mean-square speed of gas molecules: urms = ( M ) Van der waals equation; for calculating the pressure of a nonideal gas: an 2 (P + ) (V - nb) = nRT V 2 Definition of heat capacity, where s is specific heat: C = ms Calculation of heat change in terms of specific heat : q = msDt Calculation of heat change in terms of heat capacity: q = CDt q1q2 Electrical force: F = k el r2 q1q2 Potential energy: V = k r Calculation of standard enthalpy of reaction: DH˚rxn = å nDH˚f (products) - å mDH˚f (reactants) [where n and m are coefficients in equation] Mathematical statement of the first law of thermodynamics: DE = q + w Work done in gas expansion or compression: w = - PDV Definition of enthalpy: H = E + PV Enthalpy (or energy) change for a constant-pressure process: DH = DE +PDV Enthalpy (or energy) change for a constant-pressure process: DE = DH - RTDn, where n is the change in the number of moles of gas. -

C H Ap Ter 10 / R U Ssian B Ar
10 bar / Russian 10 Chapter Chapter Russian bar Written by Glen Stewart Contributors: Juan-Carlos Benitez Lucy Francis-Litton Juliette Hardy-Donaldson Sainbayar Janchividorj Darek Karczewski Sylvain Rainville André St-Jean Jarek Wojciechowski This document is published by the FEDEC European Federation of Professional Circus Schools. It is free of charges and can not be sold. 10 RUSSIAN BAR Russian bar Russian Introduction 2 Part 1. Why single bar or triple bar? 3 Part 2. Construction of the bars 4 2.1. Single bar construction 4 2.2. Triple bar construction 5 Part 3. Safety 11 3.1. Communication 11 3.2. Lunging 11 3.3. Spotting. 13 Part 4. Basics of single bar 15 4.1. Handstands on the Bar 20 4.2. Suggested skill progression for single bar 21 Part 5. Basics of triple bar 22 5.1. Bases’ posture and position. 22 5.2. The 4 tasks / stages for the base: 23 5.3. Flyer training 26 Mounting the bar. 27 Foot positioning for the flyer. 28 Initiating the jump. 29 5.4. Suggested skill progression for triple bar 30 Part 6. Trampoline Training 31 Getting the height 31 Rotation 31 Arms 31 Training habits and pointers 31 Body position on landing 32 This document is published by the FEDEC – European Federation of Professional Circus Schools. It is free of charges and can not be sold. 1 10 Introduction Russian bar Russian The purpose of this manual is to be an introduction to Russian bar and to help with the fundamental elements of Russian bar technique. The intention is that with the help of this manual, tea- chers and students will be able to construct their own bar and safely begin training bar technique. -

Cerebral Autoregulation and Response to Intravenous Thrombolysis for Acute Ischemic Stroke Ricardo C
www.nature.com/scientificreports OPEN Cerebral autoregulation and response to intravenous thrombolysis for acute ischemic stroke Ricardo C. Nogueira1,4*, Man Y. Lam2, Osian Llwyd2, Angela S. M. Salinet 1, Edson Bor‑Seng‑Shu1, Ronney B. Panerai2,3 & Thompson G. Robinson2,3 We hypothesized that knowledge of cerebral autoregulation (CA) status during recanalization therapies could guide further studies aimed at neuroprotection targeting penumbral tissue, especially in patients that do not respond to therapy. Thus, we assessed CA status of patients with acute ischemic stroke (AIS) during intravenous r-tPA therapy and associated CA with response to therapy. AIS patients eligible for intravenous r-tPA therapy were recruited. Cerebral blood fow velocities (transcranial Doppler) from middle cerebral artery and blood pressure (Finometer) were recorded to calculate the autoregulation index (ARI, as surrogate for CA). National Institute of Health Stroke Score was assessed and used to defne responders to therapy (improvement of ≥ 4 points on NIHSS measured 24–48 h after therapy). CA was considered impaired if ARI < 4. In 38 patients studied, compared to responders, non-responders had signifcantly lower ARI values (afected hemisphere: 5.0 vs. 3.6; unafected hemisphere: 5.4 vs. 4.4, p = 0.03) and more likely to have impaired CA (32% vs. 62%, p = 0.02) during thrombolysis. In conclusion, CA during thrombolysis was impaired in patients who did not respond to therapy. This variable should be investigated as a predictor of the response to therapy and to subsequent neurological outcome. Te key objective of current acute ischemic stroke (AIS) treatment is based on rapid blood fow restoration by thrombolysis, using intravenous recombinant tissue plasminogen activator (r-tPA), and/or mechanical arterial recanalization techniques1-3. -

Balinese Romanization Table
Balinese Principal consonants1 (h)a2 ᬳ ᭄ᬳ na ᬦ ᭄ᬦ ca ᬘ ᭄ᬘ᭄ᬘ ra ᬭ ᭄ᬭ ka ᬓ ᭄ᬓ da ᬤ ᭄ᬤ ta ᬢ ᭄ᬢ sa ᬲ ᭄ᬲ wa ᬯ la ᬮ ᭄ᬙ pa ᬧ ᭄ᬧ ḍa ᬟ ᭄ᬠ dha ᬥ ᭄ᬟ ja ᬚ ᭄ᬚ ya ᬬ ᭄ᬬ ña ᬜ ᭄ᬜ ma ᬫ ᭄ᬫ ga ᬕ ᭄ᬕ ba ᬩ ᭄ᬩ ṭa ᬝ ᭄ᬝ nga ᬗ ᭄ᬗ Other consonant forms3 na (ṇa) ᬡ ᭄ᬡ ca (cha) ᭄ᬙ᭄ᬙ ta (tha) ᬣ ᭄ᬣ sa (śa) ᬱ ᭄ᬱ sa (ṣa) ᬰ ᭄ᬰ pa (pha) ᬨ ᭄ᬛ ga (gha) ᬖ ᭄ᬖ ba (bha) ᬪ ᭄ᬪ ‘a ᬗ᬴ ha ᬳ᬴ kha ᬓ᬴ fa ᬧ᬴ za ᬚ᬴ gha ᬕ᬴ Vowels and other agglutinating signs4 5 a ᬅ 6 ā ᬵ ᬆ e ᬾ ᬏ ai ᬿ ᬐ ĕ ᭂ ö ᭃ i ᬶ ᬇ ī ᬷ ᬈ o ᭀ ᬑ au ᭁ ᬒ u7 ᬸ ᬉ ū ᬹ ᬊ ya, ia8 ᭄ᬬ r9 ᬃ ra ᭄ᬭ rĕ ᬋ rö ᬌ ᬻ lĕ ᬍ ᬼ lö ᬎ ᬽ h ᬄ ng ᬂ ng ᬁ Numerals 1 2 3 4 5 ᭑ ᭒ ᭓ ᭔ ᭕ 6 7 8 9 0 ᭖ ᭗ ᭘ ᭙ ᭐ 1 Each consonant has two forms, the regular and the appended, shown on the left and right respectively in the romanization table. The vowel a is implicit after all consonants and consonant clusters and should be supplied in transliteration, unless: (a) another vowel is indicated by the appropriate sign; or (b) the absence of any vowel is indicated by the use of an adeg-adeg sign ( ). (Also known as the tengenen sign; ᭄ paten in Javanese.) 2 This character often serves as a neutral seat for a vowel, in which case the h is not transcribed. -

The Brill Typeface User Guide & Complete List of Characters
The Brill Typeface User Guide & Complete List of Characters Version 2.06, October 31, 2014 Pim Rietbroek Preamble Few typefaces – if any – allow the user to access every Latin character, every IPA character, every diacritic, and to have these combine in a typographically satisfactory manner, in a range of styles (roman, italic, and more); even fewer add full support for Greek, both modern and ancient, with specialised characters that papyrologists and epigraphers need; not to mention coverage of the Slavic languages in the Cyrillic range. The Brill typeface aims to do just that, and to be a tool for all scholars in the humanities; for Brill’s authors and editors; for Brill’s staff and service providers; and finally, for anyone in need of this tool, as long as it is not used for any commercial gain.* There are several fonts in different styles, each of which has the same set of characters as all the others. The Unicode Standard is rigorously adhered to: there is no dependence on the Private Use Area (PUA), as it happens frequently in other fonts with regard to characters carrying rare diacritics or combinations of diacritics. Instead, all alphabetic characters can carry any diacritic or combination of diacritics, even stacked, with automatic correct positioning. This is made possible by the inclusion of all of Unicode’s combining characters and by the application of extensive OpenType Glyph Positioning programming. Credits The Brill fonts are an original design by John Hudson of Tiro Typeworks. Alice Savoie contributed to Brill bold and bold italic. The black-letter (‘Fraktur’) range of characters was made by Karsten Lücke. -
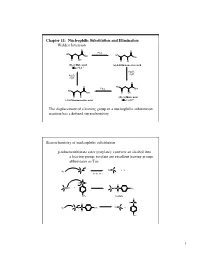
Chapter 11: Nucleophilic Substitution and Elimination Walden Inversion
Chapter 11: Nucleophilic Substitution and Elimination Walden Inversion O O PCl5 HO HO OH OH O OH O Cl (S)-(-) Malic acid (+)-2-Chlorosuccinic acid [a]D= -2.3 ° Ag2O, H2O Ag2O, H2O O O HO PCl5 OH HO OH O OH O Cl (R)-(+) Malic acid (-)-2-Chlorosuccinic acid [a]D= +2.3 ° The displacement of a leaving group in a nucleophilic substitution reaction has a defined stereochemistry Stereochemistry of nucleophilic substitution p-toluenesulfonate ester (tosylate): converts an alcohol into a leaving group; tosylate are excellent leaving groups. abbreviates as Tos C X Nu C + X- Nu: X= Cl, Br, I O Cl S O O + C OH C O S CH3 O CH3 tosylate O -O S O O Nu C + Nu: C O S CH3 O CH3 1 O Tos-Cl - H3C O O H + TosO - H O H pyridine H O Tos O CH3 [a]D= +33.0 [a]D= +31.1 [a]D= -7.06 HO- HO- O - Tos-Cl H3C O - H O O TosO + H O H pyridine Tos H O CH3 [a]D= -7.0 [a]D= -31.0 [a]D= -33.2 The nucleophilic substitution reaction “inverts” the Stereochemistry of the carbon (electrophile)- Walden inversion Kinetics of nucleophilic substitution Reaction rate: how fast (or slow) reactants are converted into product (kinetics) Reaction rates are dependent upon the concentration of the reactants. (reactions rely on molecular collisions) H H Consider: HO C _ _ C Br Br HO H H H H At a given temperature: If [OH-] is doubled, then the reaction rate may be doubled If [CH3-Br] is doubled, then the reaction rate may be doubled A linear dependence of rate on the concentration of two reactants is called a second-order reaction (molecularity) 2 H H HO C _ _ C Br Br HO H H H H Reaction rates (kinetic) can be expressed mathematically: reaction rate = disappearance of reactants (or appearance of products) For the disappearance of reactants: - rate = k [CH3Br] [OH ] [CH3Br] = CH3Br concentration [OH-] = OH- concentration k= constant (rate constant) L mol•sec For the reaction above, product formation involves a collision between both reactants, thus the rate of the reaction is dependent upon the concentration of both. -

H(X) = F (X)+ G(X) → Dh Dx = Df Dx + Dg Dx B(Z)
MAT1193 – 5c Sum, Product and Quotient Rules In this set of notes, we will consider the rules for applying derivatives to three basic ways for combining functions. Remember that there are three perspectives that we can take on each of our rule for the derivative: 1. The derivation of the rule; 2. An intuition for the rule; 3. The application of the rule. We will try to get some insight (1 & 2) into the sum and product rules, but not for the quotient rule. To start, lets just state the rules. I will use both the prime notation and the differential notation. Sum rule - the derivative of the sum of two functions is the sum of the derivative of each function: h(x) = f (x) + g(x) →h# ( x) = f #( x) + g# ( x) dh df dg h(x) = f (x) + g(x) → = + dx dx dx Here are some examples: b(z) = z3 + z2 →b# ( z) = 3z2 + 2z € 3/2 −1 dp d q d q 3 3 p(q) = q3/2 + q−1 → = ( ) + ( ) = q1/2 + (−1)q−2 = q1/2 − q−2 dq dq dq 2 2 € Constant sum rule - the derivative of the sum of a function and a constant value is equal to the derivative of the function alone: h(x) = f (x) + a →h# ( x) = f #( x) dh df h(x) = f (x) + a → = dx dx Examples: f (x) = z3 + 345 → f #( x) = 3x 2 € da a(l) = l−7 − 0.17 → = −7l−8 dl € This is actually a special case of the sum rule, since we can view the constant as g(x) = a resulting from the constant function and just plug in to the sum rule.