Distinguishing Mathematics Notation from English Text Using Computational Geometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J
Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J. Keely. All Rights Reserved. Mathematical expressions can be typed online in a number of ways including plain text, ASCII codes, HTML tags, or using an equation editor (see Writing Mathematical Notation Online for overview). If the application in which you are working does not have an equation editor built in, then a common option is to write expressions horizontally in plain text. In doing so you have to format the expressions very carefully using appropriately placed parentheses and accurate notation. This document provides examples and important cautions for writing mathematical expressions in plain text. Section 1. How to Write Exponents Just as on a graphing calculator, when writing in plain text the caret key ^ (above the 6 on a qwerty keyboard) means that an exponent follows. For example x2 would be written as x^2. Example 1a. 4xy23 would be written as 4 x^2 y^3 or with the multiplication mark as 4*x^2*y^3. Example 1b. With more than one item in the exponent you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x2n must be written as x^(2n) and NOT as x^2n. Writing x^2n means xn2 . Example 1c. When using the quotient rule of exponents you often have to perform subtraction within an exponent. In such cases you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x5 The middle step of ==xx52− 3 must be written as x^(5-2) and NOT as x^5-2 which means x5 − 2 . -

The Recent Trademarking of Pi: a Troubling Precedent
The recent trademarking of Pi: a troubling precedent Jonathan M. Borwein∗ David H. Baileyy July 15, 2014 1 Background Intellectual property law is complex and varies from jurisdiction to jurisdiction, but, roughly speaking, creative works can be copyrighted, while inventions and processes can be patented, and brand names thence protected. In each case the intention is to protect the value of the owner's work or possession. For the most part mathematics is excluded by the Berne convention [1] of the World Intellectual Property Organization WIPO [12]. An unusual exception was the successful patenting of Gray codes in 1953 [3]. More usual was the carefully timed Pi Day 2012 dismissal [6] by a US judge of a copyright infringement suit regarding π, since \Pi is a non-copyrightable fact." We mathematicians have largely ignored patents and, to the degree we care at all, have been more concerned about copyright as described in the work of the International Mathematical Union's Committee on Electronic Information and Communication (CEIC) [2].1 But, as the following story indicates, it may now be time for mathematicians to start paying attention to patenting. 2 Pi period (π:) In January 2014, the U.S. Patent and Trademark Office granted Brooklyn artist Paul Ingrisano a trademark on his design \consisting of the Greek letter Pi, followed by a period." It should be noted here that there is nothing stylistic or in any way particular in Ingrisano's trademark | it is simply a standard Greek π letter, followed by a period. That's it | π period. No one doubts the enormous value of Apple's partly-eaten apple or the MacDonald's arch. -

Fundamentals of Mathematics Lecture 3: Mathematical Notation Guan-Shieng Fundamentals of Mathematics Huang Lecture 3: Mathematical Notation References
Fundamentals of Mathematics Lecture 3: Mathematical Notation Guan-Shieng Fundamentals of Mathematics Huang Lecture 3: Mathematical Notation References Guan-Shieng Huang National Chi Nan University, Taiwan Spring, 2008 1 / 22 Greek Letters I Fundamentals of Mathematics 1 A, α, Alpha Lecture 3: Mathematical 2 B, β, Beta Notation Guan-Shieng 3 Γ, γ, Gamma Huang 4 ∆, δ, Delta References 5 E, , Epsilon 6 Z, ζ, Zeta 7 H, η, Eta 8 Θ, θ, Theta 9 I , ι, Iota 10 K, κ, Kappa 11 Λ, λ, Lambda 12 M, µ, Mu 2 / 22 Greek Letters II Fundamentals 13 of N, ν, Nu Mathematics Lecture 3: 14 Ξ, ξ, Xi Mathematical Notation 15 O, o, Omicron Guan-Shieng Huang 16 Π, π, Pi References 17 P, ρ, Rho 18 Σ, σ, Sigma 19 T , τ, Tau 20 Υ, υ, Upsilon 21 Φ, φ, Phi 22 X , χ, Chi 23 Ψ, ψ, Psi 24 Ω, ω, Omega 3 / 22 Logic I Fundamentals of • Conjunction: p ∧ q, p · q, p&q (p and q) Mathematics Lecture 3: Mathematical • Disjunction: p ∨ q, p + q, p|q (p or q) Notation • Conditional: p → q, p ⇒ q, p ⊃ q (p implies q) Guan-Shieng Huang • Biconditional: p ↔ q, p ⇔ q (p if and only if q) References • Exclusive-or: p ⊕ q, p + q • Universal quantifier: ∀ (for all) • Existential quantifier: ∃ (there is, there exists) • Unique existential quantifier: ∃! 4 / 22 Logic II Fundamentals of Mathematics Lecture 3: Mathematical Notation Guan-Shieng • p → q ≡ ¬p ∨ q Huang • ¬(p ∨ q) ≡ ¬p ∧ ¬q, ¬(p ∧ q) ≡ ¬p ∨ ¬q References • ¬∀x P(x) ≡ ∃x ¬P(x), ¬∃x P(x) ≡ ∀x ¬P(x) • ∀x ∃y P(x, y) 6≡ ∃y ∀x P(x, y) in general • p ⊕ q ≡ (p ∧ ¬q) ∨ (¬p ∧ q) 5 / 22 Set Theory I Fundamentals of Mathematics • Empty set: ∅, {} Lecture 3: Mathematical • roster: S = {a , a ,..., a } Notation 1 2 n Guan-Shieng defining predicate: S = {x| P(x)} where P is a predicate Huang recursive description References • N: natural numbers Z: integers R: real numbers C: complex numbers • Two sets A and B are equal if x ∈ A ⇔ x ∈ B. -
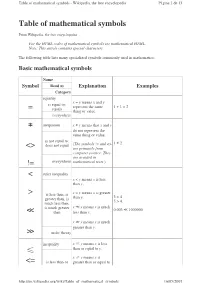
Table of Mathematical Symbols = ≠ <> != < > ≪ ≫ ≤ <=
Table of mathematical symbols - Wikipedia, the free encyclopedia Página 1 de 13 Table of mathematical symbols From Wikipedia, the free encyclopedia For the HTML codes of mathematical symbols see mathematical HTML. Note: This article contains special characters. The following table lists many specialized symbols commonly used in mathematics. Basic mathematical symbols Name Symbol Read as Explanation Examples Category equality x = y means x and y is equal to; represent the same 1 + 1 = 2 = equals thing or value. everywhere ≠ inequation x ≠ y means that x and y do not represent the same thing or value. is not equal to; 1 ≠ 2 does not equal (The symbols != and <> <> are primarily from computer science. They are avoided in != everywhere mathematical texts. ) < strict inequality x < y means x is less than y. > is less than, is x > y means x is greater 3 < 4 greater than, is than y. 5 > 4. much less than, is much greater x ≪ y means x is much 0.003 ≪ 1000000 ≪ than less than y. x ≫ y means x is much greater than y. ≫ order theory inequality x ≤ y means x is less than or equal to y. ≤ x ≥ y means x is <= is less than or greater than or equal to http://en.wikipedia.org/wiki/Table_of_mathematical_symbols 16/05/2007 Table of mathematical symbols - Wikipedia, the free encyclopedia Página 2 de 13 equal to, is y. greater than or The symbols and equal to ( <= 3 ≤ 4 and 5 ≤ 5 ≥ >= are primarily from 5 ≥ 4 and 5 ≥ 5 computer science. They >= order theory are avoided in mathematical texts. -

Outline of Mathematics
Outline of mathematics The following outline is provided as an overview of and 1.2.2 Reference databases topical guide to mathematics: • Mathematical Reviews – journal and online database Mathematics is a field of study that investigates topics published by the American Mathematical Society such as number, space, structure, and change. For more (AMS) that contains brief synopses (and occasion- on the relationship between mathematics and science, re- ally evaluations) of many articles in mathematics, fer to the article on science. statistics and theoretical computer science. • Zentralblatt MATH – service providing reviews and 1 Nature of mathematics abstracts for articles in pure and applied mathemat- ics, published by Springer Science+Business Media. • Definitions of mathematics – Mathematics has no It is a major international reviewing service which generally accepted definition. Different schools of covers the entire field of mathematics. It uses the thought, particularly in philosophy, have put forth Mathematics Subject Classification codes for orga- radically different definitions, all of which are con- nizing their reviews by topic. troversial. • Philosophy of mathematics – its aim is to provide an account of the nature and methodology of math- 2 Subjects ematics and to understand the place of mathematics in people’s lives. 2.1 Quantity Quantity – 1.1 Mathematics is • an academic discipline – branch of knowledge that • Arithmetic – is taught at all levels of education and researched • Natural numbers – typically at the college or university level. Disci- plines are defined (in part), and recognized by the • Integers – academic journals in which research is published, and the learned societies and academic departments • Rational numbers – or faculties to which their practitioners belong. -

List of Mathematical Symbols by Subject from Wikipedia, the Free Encyclopedia
List of mathematical symbols by subject From Wikipedia, the free encyclopedia This list of mathematical symbols by subject shows a selection of the most common symbols that are used in modern mathematical notation within formulas, grouped by mathematical topic. As it is virtually impossible to list all the symbols ever used in mathematics, only those symbols which occur often in mathematics or mathematics education are included. Many of the characters are standardized, for example in DIN 1302 General mathematical symbols or DIN EN ISO 80000-2 Quantities and units – Part 2: Mathematical signs for science and technology. The following list is largely limited to non-alphanumeric characters. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can be found in the respective linked articles. Contents 1 Guide 2 Set theory 2.1 Definition symbols 2.2 Set construction 2.3 Set operations 2.4 Set relations 2.5 Number sets 2.6 Cardinality 3 Arithmetic 3.1 Arithmetic operators 3.2 Equality signs 3.3 Comparison 3.4 Divisibility 3.5 Intervals 3.6 Elementary functions 3.7 Complex numbers 3.8 Mathematical constants 4 Calculus 4.1 Sequences and series 4.2 Functions 4.3 Limits 4.4 Asymptotic behaviour 4.5 Differential calculus 4.6 Integral calculus 4.7 Vector calculus 4.8 Topology 4.9 Functional analysis 5 Linear algebra and geometry 5.1 Elementary geometry 5.2 Vectors and matrices 5.3 Vector calculus 5.4 Matrix calculus 5.5 Vector spaces 6 Algebra 6.1 Relations 6.2 Group theory 6.3 Field theory 6.4 Ring theory 7 Combinatorics 8 Stochastics 8.1 Probability theory 8.2 Statistics 9 Logic 9.1 Operators 9.2 Quantifiers 9.3 Deduction symbols 10 See also 11 References 12 External links Guide The following information is provided for each mathematical symbol: Symbol: The symbol as it is represented by LaTeX. -

Towards a Better Notation for Mathematics
Towards a Better Notation for Mathematics Christopher Olah ([email protected]) July 8, 2010 Abstract: This paper explores alternative notations for mathe- matics. We consider numerical notations that make arithmetic eas- ier, a notation for quantifiers that reduces the number of variables one needs to track, and many other ideas. (Regarding Notation: The typographical quality of new sym- bols introduced in this paper is terribly lacking { you will likely need to zoom in on them to see them well. This is because the author is injecting them as images. A font is in the works but isn't much better, as the author is not a skilled font-craft.) Update: I've made some minor changes to young-me's work to clean things up a bit. That said, please keep in mind that I've progressed a long way since writing this and it isn't representative of my current abilities. Contents 1 Introduction2 2 Version Representation3 3 Numbers & Vectors3 4 Sets5 5 Boolean Operations6 6 Standard Functions6 7 Trigonometry7 8 Calculus8 9 Quantifiers8 1 10 Science9 11 Equality, Scope & Algebra9 1 Introduction When one considers how complicated the ideas mathematical notation must represent are, it clearly does quite a good job. Despite this, the author believes that any claim that modern mathematical notation is the best should be met with extreme scepticism. Mathematical notation is a natural language: no one sat down and con- structed it, but rather it formed gradually by people making changes that are adopted. Most changes are not adopted; whether they are depends on a variety of factors including: mathematical utility, ease of adoption (the average individ- ual doesn't want to spend hours learning), dissemination, and shear dumb luck. -

Unicode Nearly Plain Text Encoding of Mathematics
Unicode Nearly Plain Text Encoding of Mathematics Unicode Nearly Plain-Text Encoding of Mathematics Murray Sargent III Office Authoring Services, Microsoft Corporation 28-Aug-06 1. Introduction ............................................................................................................ 2 2. Encoding Simple Math Expressions ...................................................................... 3 2.1 Fractions .......................................................................................................... 4 2.2 Subscripts and Superscripts........................................................................... 6 2.3 Use of the Blank (Space) Character ............................................................... 7 3. Encoding Other Math Expressions ........................................................................ 8 3.1 Delimiters ........................................................................................................ 8 3.2 Literal Operators ........................................................................................... 10 3.3 Prescripts and Above/Below Scripts .......................................................... 11 3.4 n-ary Operators ............................................................................................. 11 3.5 Mathematical Functions ............................................................................... 12 3.6 Square Roots and Radicals ........................................................................... 13 3.7 Enclosures .................................................................................................... -

A Guide to Writing Mathematics
A Guide to Writing Mathematics Dr. Kevin P. Lee Introduction This is a math class! Why are we writing? There is a good chance that you have never written a paper in a math class before. So you might be wondering why writing is required in your math class now. The Greek word mathemas, from which we derive the word mathematics, embodies the notions of knowledge, cognition, understanding, and perception. In the end, mathematics is about ideas. In math classes at the university level, the ideas and concepts encountered are more complex and sophisticated. The mathematics learned in college will include concepts which cannot be expressed using just equations and formulas. Putting mathemas on paper will require writing sentences and paragraphs in addition to the equations and formulas. Mathematicians actually spend a great deal of time writing. If a mathematician wants to contribute to the greater body of mathematical knowledge, she must be able communicate her ideas in a way which is comprehensible to others. Thus, being able to write clearly is as important a mathematical skill as being able to solve equations. Mastering the ability to write clear mathematical explanations is important for non-mathematicians as well. As you continue taking math courses in college, you will come to know more mathematics than most other people. When you use your mathematical knowledge in the future, you may be required to explain your thinking process to another person (like your boss, a co-worker, or an elected official), and it will be quite likely that this other person will know less math than you do. -

Mathematical Symbols and Abbreviations Mccp-Matthews-Symbols-001 This Leaflet Provides Information on Symbols and Notation Commonly Used in Mathematics
community project Mathematical Symbols and Abbreviations mccp-matthews-symbols-001 This leaflet provides information on symbols and notation commonly used in mathematics. It is designed to enable further information to be found from resources in mathcentre (www.mathcentre.ac.uk). In the table below, the symbol or notation is given in column one. It is not always obvious how the combination of characters used in mathematical notation is said, so where appropriate this information is given in column two. Column three explains the use of the symbol and an example may be given for further explanation in column four. The last column contains a phrase to be entered as a search topic in mathcentremathcentre if further details are required. community project Care should be taken as context is important.encouraging Identical math academicsematical to symbols share and maths notation support are used resources in different circumstances to convey very different ideas. All mccp resources are released under a Creative Commons licence Symbol Say Means Example mathcentre Search Topic P sigma Represents summation “Sigma notation” Parallel In the same direction as “The gradient of a straight k line segment” || Modulus, absolute The size of a number, ignoring the sign |3|= 3, | 3|= 3 Modulus (vertical lines, ei- value − ther side of a num- ber or variable) |A| Determinant of Determinant of matrix A Determinants matrix A det (A) Determinant of Determinant of matrix A Determinants matrix A c Janette Matthews Tony Croft www.mathcentre.ac.uk Loughborough University Loughborough University community project Mathematical Symbols and Abbreviations (continued) Symbol Say Means Example mathcentre Search Topic () brackets Used in many different contexts e.g. -

Mathematics Review for Science Students
Mathematics Review for Science Students Math Department Math Study Center Grossmont College 1. 0 - Exponents and Scientific Notation 1.1 - Exponential Notation Exponential notation is a simple mathematical notation to represent repeated multiplication of the same number. Numbers in exponential notation are written in the form x n , where x is the base and n is the exponent. Examples: 1. 34 = 3×3×3×3 = 81 2. 103 =10×10×10 =1000 1.2 - Some Rules of Exponents m n m+n 1. x x x −n 1 ⋅ = 3. x = for x ≠ 0 x n m x m−n 2. = x 0 x n 4. x =1 for x ≠ 0 Examples: 3 4 3+4 7 1. 10 10 10 10 −2 1 1 × = = 5. 3 = = 32 9 2. 10−2 ×105 =10−2+5 =103 1 1 1 6. 10−4 = = = 106 104 10⋅10⋅10⋅10 10000 3. =106−3 =103 103 7. 40 =1 7 10 7−(−4) 7+4 11 4. =10 =10 =10 0 10−4 8. 10 =1 1.3 - Scientific Notation Scientific notation is shorthand for writing very large and very small numbers. Proper scientific notation is written using powers of 10 and is in the form N ×10m where N is a number greater than or equal to 1 but less than 10 (1 ≤ N <10 ) and m is the exponent. For example, the speed of light,1.86 ×105 miles per second is in scientific notation but 18.6 ×104 is not since N which is 18.6 is not between 1 and 10. -

Mathematical Symbols
List of mathematical symbols This is a list of symbols used in all branches ofmathematics to express a formula or to represent aconstant . A mathematical concept is independent of the symbol chosen to represent it. For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations, a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. However, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas. In short, convention dictates the meaning. Each symbol is shown both inHTML , whose display depends on the browser's access to an appropriate font installed on the particular device, and typeset as an image usingTeX . Contents Guide Basic symbols Symbols based on equality Symbols that point left or right Brackets Other non-letter symbols Letter-based symbols Letter modifiers Symbols based on Latin letters Symbols based on Hebrew or Greek letters Variations See also References External links Guide This list is organized by symbol type and is intended to facilitate finding an unfamiliar symbol by its visual appearance. For a related list organized by mathematical topic, see List of mathematical symbols by subject. That list also includes LaTeX and HTML markup, and Unicode code points for each symbol (note that this article doesn't