DOCSLIB.ORG

Mathematical Symbols

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mathematical Symbols List of mathematical symbols This is a list of symbols used in all branches ofmathematics to express a formula or to represent aconstant . A mathematical concept is independent of the symbol chosen to represent it. For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations, a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. However, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas. In short, convention dictates the meaning. Each symbol is shown both inHTML , whose display depends on the browser's access to an appropriate font installed on the particular device, and typeset as an image usingTeX . Contents Guide Basic symbols Symbols based on equality Symbols that point left or right Brackets Other non-letter symbols Letter-based symbols Letter modifiers Symbols based on Latin letters Symbols based on Hebrew or Greek letters Variations See also References External links Guide This list is organized by symbol type and is intended to facilitate finding an unfamiliar symbol by its visual appearance. For a related list organized by mathematical topic, see List of mathematical symbols by subject. That list also includes LaTeX and HTML markup, and Unicode code points for each symbol (note that this article doesn't have the latter two, but they could certainly be added). There is a Wikibooks guide for using maths in LaTeX,[1] and a comprehensive LaTeX symbol list.[2] It is also possible to check to see if a Unicode code point is available as a LaTeX command, or vice versa.[3] Also note that where there is no LaTeX command natively available for a particular symbol (although there may be options that require adding packages), the symbol could be added via other options, such as setting the document up to support Unicode,[4] and entering the character in a variety of ways (e.g. copying and pasting, keyboard shortcuts, the \unicode{<insertcodepoint>} command[5]) as well as other options[6] and extensive additional information.[7][8] Basic symbols: Symbols widely used in mathematics, roughly through first-year calculus. More advanced meanings are included with some symbols listed here. Symbols based on equality "=": Symbols derived from or similar to the equal sign, including double-headed arrows. Not surprisingly these symbols are often associated with an equivalence relation. Symbols that point left or right: Symbols, such as < and >, that appear to point to one side or another. Brackets: Symbols that are placed on either side of a variable or expression, such as|x |. Other non-letter symbols: Symbols that do not fall in any of the other categories. Letter-based symbols: Many mathematical symbols are based on, or closely resemble, a letter in some alphabet. This section includes such symbols, including symbols that resemble upside-down letters. Many letters have conventional meanings in various branches of mathematics and physics. These are not listed here. TheSee also section, below, has several lists of such usages. Letter modifiers: Symbols that can be placed on or next to any letter to modify the letter's meaning. Symbols based on Latin letters, including those symbols that resemble or contain anX .δ, Δ, π, Π, σ, Σ, Φ. Note: symbols resembling Λ are grouped with "V" under Latin letters ,ב ,א .Symbols based on Hebrew or Greek letters e.g Variations: Usage in languages written right-to-left Basic symbols Name Symbol Symbol Read as Explanation Examples in HTML in TeX Category addition plus; means the sum of and . add 4 + 6 4 6 2 + 7 = 9 arithmetic + disjoint union the disjoint A1 + A2 means the disjoint union of A1 = {3, 4, 5, 6} ∧ A2 = {7, 8, 9, 10} ⇒ union of ... sets and . and ... A1 A2 A1 + A2 = {(3, 1), (4, 1), (5, 1), (6, 1), (7, 2), (8, 2), (9, 2), (10, 2)} set theory subtraction minus; 36 − 11 means the subtraction of11 take; 36 − 11 = 25 from . subtract 36 arithmetic negative sign negative; minus; −3 means the additive inverse of the −(−5) = 5 − the opposite number 3. of arithmetic set-theoretic A − B means the set that contains all complement the elements of A that are not in B. minus; {1, 2, 4} − {1, 3, 4} = {2} without (∖ can also be used for set-theoretic set theory complement as described below.) plus-minus plus or minus 6 ± 3 means both 6 + 3 and 6 − 3. The equation x = 5 ± √4, has two solutions, x = 7 and x = 3. arithmetic ± \pm plus-minus 10 ± 2 or equivalently 10 ± 20% plus or minus means the range from 10 − 2 to If a = 100 ± 1 mm, then a ≥ 99 mm and a ≤ 101 mm. measurement 10 + 2. minus-plus 6 ± (3 ∓ 5) means 6 + (3 − 5) and minus or plus cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y). ∓ \mp 6 − (3 + 5). arithmetic multiplication times; 3 × 4 or 3 ⋅ 4 means the multiplication 7 ⋅ 8 = 56 multiplied by of 3 by 4. arithmetic dot product scalar product dot u ⋅ v means the dot product ofvectors (1, 2, 5) ⋅ (3, 4, −1) = 6 linear algebra u and v × vector algebra \times ⋅ cross product vector \cdot product i j k u × v means the cross product of cross (1, 2, 5) × (3, 4, −1) = 1 2 5 = (−22, 16, −2) · vectors u and v linear algebra 3 4 −1 vector algebra placeholder A · means a placeholder for an argument of a function. Indicates the (silent) functional nature of an expression | · | functional without assigning a specific symbol for analysis an argument. division (Obelus) 2 ÷ 4 = 0.5 6 ÷ 3 or 6 ⁄ 3 means the division of 6 divided by; by 3. over 12 ⁄ 4 = 3 arithmetic ÷ \div quotient group G / H means the quotient of groupG {0, a, 2a, b, b + a, b + 2a} / {0, b} = {{0, b}, {a, b + a}, {2a, b + 2a}} ⁄ mod modulo its subgroup H. group theory quotient set A/~ means the set of all ~ equivalence If we define ~ by x ~ y ⇔ x − y ∈ ℤ, then mod classes in A. ℝ/~ = {x + n : n ∈ ℤ, x ∈ [0,1)}. set theory square root (radical symbol) √x means the nonnegative number √4 = 2 the (principal) whose square is x. square root of \surd real numbers √ complex \sqrt{x} square root If z = r exp(iφ) is represented in polar the (complex) coordinates with , then square root of −π < φ ≤ π √−1 = i √z = √r exp(iφ/2). complex numbers summation ∑ \sum sum over ... from ... to ... means . of calculus indefinite integral or antiderivative indefinite integral of ∫ f(x) dx means a function whose - OR - derivative is f. the antiderivative of calculus definite integral b integral from f(x) dx means the signed area ∫ \int ∫ a b 2 b3 − a3 ... to ... of ... x dx = between the x-axis and the graph of the ∫ a 3 with respect function f between x = a and x = b. to calculus f ds means the integral of f along line integral ∫ C b line/ path/ the curve C, ∫ f(r(t)) |r'(t)| dt, where curve/ integral a r is a parametrization of C. (If the curve of ... along ... calculus is closed, the symbol ∮ may be used instead, as described below.) Similar to the integral, but used to denote a single integration over a closed curve or loop. It is sometimes used in physics texts involving equations regarding Gauss's Law, and while these formulas involve a closed surface integral, the representations describe only the first integration of the volume over the enclosing surface. Instances where the latter requires simultaneous double integration, the Contour symbol ∯ would be more appropriate. integral; A third related symbol is the closed closed line volume integral, denoted by the symbol integral 1 If is a Jordan curve about 0, then . ∰ . C ∮ C z dz = 2πi ∮ \oint contour integral of The contour integral can also frequently calculus be found with a subscript capital letter C, ∮ C, denoting that a closed loop integral is, in fact, around a contour C, or sometimes dually appropriately, a circle C. In representations of Gauss's Law, a subscript capital S, ∮ S, is used to denote that the integration is over a closed surface. … \ldots ⋯ \cdots ellipsis ⋮ and so forth Indicates omitted values from a pattern. 1/2 + 1/4 + 1/8 + 1/16 + ⋯ = 1 everywhere \vdots ⋰ ⋱ \ddots therefore therefore; Sometimes used in proofs before so; All humans are mortal. Socrates is a human.∴ Socrates is mortal. ∴ \therefore logical consequences. hence everywhere because because; Sometimes used in proofs before 11 is prime ∵ it has no positive integer factors other than itself and one. ∵ \because since reasoning. everywhere ! factorial factorial means the product . combinatorics logical The statement !A is true if and only if A !(!A) ⇔ A negation is false. x ≠ y ⇔ !(x = y) not A slash placed through another propositional operator is the same as "!" placed in logic front. (The symbol ! is primarily from computer science. It is avoided in mathematical texts, where the notation ¬A is preferred.) The statement ¬A is true if and only if A is false. logical A slash placed through another ¬ negation operator is the same as "¬" placed in \neg ¬(¬A) ⇔ A not front. x ≠ y ⇔ ¬(x = y) ˜ propositional logic (The symbol ~ has many other uses, so ¬ or the slash notation is preferred. Computer scientists will often use ! but this is avoided in mathematical texts.) proportionality is proportional y ∝ x means that y = kx for some to; if y = 2x, then y ∝ x.
Load more

Recommended publications
  • Math 317: Linear Algebra Notes and Problems
    Math 317: Linear Algebra Notes and Problems Nicholas Long SFASU Contents Introduction iv 1 Efficiently Solving Systems of Linear Equations and Matrix Op- erations 1 1.1 Warmup Problems . .1 1.2 Solving Linear Systems . .3 1.2.1 Geometric Interpretation of a Solution Set . .9 1.3 Vector and Matrix Equations . 11 1.4 Solution Sets of Linear Systems . 15 1.5 Applications . 18 1.6 Matrix operations . 20 1.6.1 Special Types of Matrices . 21 1.6.2 Matrix Multiplication . 22 2 Vector Spaces 25 2.1 Subspaces . 28 2.2 Span . 29 2.3 Linear Independence . 31 2.4 Linear Transformations . 33 2.5 Applications . 38 3 Connecting Ideas 40 3.1 Basis and Dimension . 40 3.1.1 rank and nullity . 41 3.1.2 Coordinate Vectors relative to a basis . 42 3.2 Invertible Matrices . 44 3.2.1 Elementary Matrices . 44 ii CONTENTS iii 3.2.2 Computing Inverses . 45 3.2.3 Invertible Matrix Theorem . 46 3.3 Invertible Linear Transformations . 47 3.4 LU factorization of matrices . 48 3.5 Determinants . 49 3.5.1 Computing Determinants . 49 3.5.2 Properties of Determinants . 51 3.6 Eigenvalues and Eigenvectors . 52 3.6.1 Diagonalizability . 55 3.6.2 Eigenvalues and Eigenvectors of Linear Transfor- mations . 56 4 Inner Product Spaces 58 4.1 Inner Products . 58 4.2 Orthogonal Complements . 59 4.3 QR Decompositions . 59 Nicholas Long Introduction In this course you will learn about linear algebra by solving a carefully designed sequence of problems. It is important that you understand every problem and proof.
    [Show full text]
  • 500 Natural Sciences and Mathematics
    500 500 Natural sciences and mathematics Natural sciences: sciences that deal with matter and energy, or with objects and processes observable in nature Class here interdisciplinary works on natural and applied sciences Class natural history in 508. Class scientific principles of a subject with the subject, plus notation 01 from Table 1, e.g., scientific principles of photography 770.1 For government policy on science, see 338.9; for applied sciences, see 600 See Manual at 231.7 vs. 213, 500, 576.8; also at 338.9 vs. 352.7, 500; also at 500 vs. 001 SUMMARY 500.2–.8 [Physical sciences, space sciences, groups of people] 501–509 Standard subdivisions and natural history 510 Mathematics 520 Astronomy and allied sciences 530 Physics 540 Chemistry and allied sciences 550 Earth sciences 560 Paleontology 570 Biology 580 Plants 590 Animals .2 Physical sciences For astronomy and allied sciences, see 520; for physics, see 530; for chemistry and allied sciences, see 540; for earth sciences, see 550 .5 Space sciences For astronomy, see 520; for earth sciences in other worlds, see 550. For space sciences aspects of a specific subject, see the subject, plus notation 091 from Table 1, e.g., chemical reactions in space 541.390919 See Manual at 520 vs. 500.5, 523.1, 530.1, 919.9 .8 Groups of people Add to base number 500.8 the numbers following —08 in notation 081–089 from Table 1, e.g., women in science 500.82 501 Philosophy and theory Class scientific method as a general research technique in 001.4; class scientific method applied in the natural sciences in 507.2 502 Miscellany 577 502 Dewey Decimal Classification 502 .8 Auxiliary techniques and procedures; apparatus, equipment, materials Including microscopy; microscopes; interdisciplinary works on microscopy Class stereology with compound microscopes, stereology with electron microscopes in 502; class interdisciplinary works on photomicrography in 778.3 For manufacture of microscopes, see 681.
    [Show full text]
  • Tilde-Arrow-Out (~→O)
    Chapter 5: Derivations in Sentential Logic 181 atomic). In the next example, the disjunction is complex (its disjuncts are not atomic). Example 2 (1) (P ´ Q) → (P & Q) Pr (2) •: (P & Q) ∨ (~P & ~Q) ID (3) |~[(P & Q) ∨ (~P & ~Q)] As (4) |•: ¸ DD (5) ||~(P & Q) 3,~∨O (6) ||~(~P & ~Q) 3,~∨O (7) ||~(P ∨ Q) 1,5,→O (8) ||~P 7,~∨O (9) ||~Q 7,~∨O (10) ||~P & ~Q 8,9,&I (11) ||¸ 6,10,¸I The basic strategy is exactly like the previous problem. The only difference is that the formulas are more complex. 13. FURTHER RULES In the previous section, we added the rule ~∨O to our list of inference rules. Although it is not strictly required, it does make a number of derivations much easier. In the present section, for the sake of symmetry, we add corresponding rules for the remaining two-place connectives; specifically, we add ~&O, ~→O, and ~↔O. That way, we have a rule for handling any negated molecular formula. Also, we add one more rule that is sometimes useful, the Rule of Repetition. The additional negation rules are given as follows. Tilde-Ampersand-Out (~&O) ~(d & e) ––––––––– d → ~e Tilde-Arrow-Out (~→O) ~(d → f) –––––––––– d & ~f 182 Hardegree, Symbolic Logic Tilde-Double-Arrow-Out (~±O) ~(d ± e) –––––––––– ~d ± e The reader is urged to verify that these are all valid argument forms of sentential logic. There are other valid forms that could serve equally well as the rules in question. The choice is to a certain arbitrary. The advantage of the particular choice becomes more apparent in a later chapter on predicate logic.
    [Show full text]
  • Notes, Since the Quadratic Form Associated with an Inner Product (Kuk2 = Hu, Ui) Must Be Positive Def- Inite
    Bindel, Spring 2012 Intro to Scientific Computing (CS 3220) Week 3: Wednesday, Feb 8 Spaces and bases 1 n I have two favorite vector spaces : R and the space Pd of polynomials of degree at most d. For Rn, we have a canonical basis: n R = spanfe1; e2; : : : ; eng; where ek is the kth column of the identity matrix. This basis is frequently convenient both for analysis and for computation. For Pd, an obvious- seeming choice of basis is the power basis: 2 d Pd = spanf1; x; x ; : : : ; x g: But this obvious-looking choice turns out to often be terrible for computation. Why? The short version is that powers of x aren't all that strongly linearly dependent, but we need to develop some more concepts before that short description will make much sense. The range space of a matrix or a linear map A is just the set of vectors y that can be written in the form y = Ax. If A is full (column) rank, then the columns of A are linearly independent, and they form a basis for the range space. Otherwise, A is rank-deficient, and there is a non-trivial null space consisting of vectors x such that Ax = 0. Rank deficiency is a delicate property2. For example, consider the matrix 1 1 A = : 1 1 This matrix is rank deficient, but the matrix 1 + δ 1 A^ = : 1 1 is not rank deficient for any δ 6= 0. Technically, the columns of A^ form a basis for R2, but we should be disturbed by the fact that A^ is so close to a singular matrix.
    [Show full text]
  • Proposal to Add U+2B95 Rightwards Black Arrow to Unicode Emoji
    Proposal to add U+2B95 Rightwards Black Arrow to Unicode Emoji J. S. Choi, 2015‐12‐12 Abstract In the Unicode Standard 7.0 from 2014, ⮕ U+2B95 was added with the intent to complete the family of black arrows encoded by ⬅⬆⬇ U+2B05–U+2B07. However, due to historical timing, ⮕ U+2B95 was not yet encoded when the Unicode Emoji were frst encoded in 2009–2010, and thus the family of four emoji black arrows were mapped not only to ⬅⬆⬇ U+2B05–U+2B07 but also to ➡ U+27A1—a compatibility character for ITC Zapf Dingbats—instead of ⮕ U+2B95. It is thus proposed that ⮕ U+2B95 be added to the set of Unicode emoji characters and be given emoji‐ and text‐style standardized variants, in order to match the properties of its siblings ⬅⬆⬇ U+2B05–U+2B07, with which it is explicitly unifed. 1 Introduction Tis document primarily discusses fve encoded characters, already in Unicode as of 2015: ⮕ U+2B95 Rightwards Black Arrow: Te main encoded character being discussed. Located in the Miscellaneous Symbols and Arrows block. ⬅⬆⬇ U+2B05–U+2B07 Leftwards, Upwards, and Downwards Black Arrow: Te three black arrows that ⮕ U+2B95 completes. Also located in the Miscellaneous Symbols and Arrows block. ➡ U+27A1 Black Rightwards Arrow: A compatibility character for ITC Zapf Dingbats. Located in the Dingbats block. Tis document proposes the addition of ⮕ U+2B95 to the set of emoji characters as defned by Unicode Technical Report (UTR) #51: “Unicode Emoji”. In other words, it proposes: 1. A property change: ⮕ U+2B95 should be given the Emoji property defned in UTR #51.
    [Show full text]
  • Dimension Formulas for the Hyperfunction Solutions to Holonomic D-Modules
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector ARTICLE IN PRESS Advances in Mathematics 180 (2003) 134–145 http://www.elsevier.com/locate/aim Dimension formulas for the hyperfunction solutions to holonomic D-modules Kiyoshi Takeuchi Institute of Mathematics, University of Tsukuba, 1-1-1, Tennodai, Tsukuba, Ibaraki 305-8571, Japan Received 15 July 2002; accepted 19 November 2002 Communicated by Takahiro Kawai Dedicated to Professor Mitsuo Morimoto on the Occasion of his 60th Birthday Abstract In this paper, we will prove an explicit dimension formula for the hyperfunction solutions to a class of holonomic D-modules. This dimension formula can be considered as a higher dimensional analogue of a beautiful theorem on ordinary differential equations due to Kashiwara (Master’s Thesis, University of Tokyo, 1970) and Komatsu (J. Fac. Sci. Univ. Tokyo Math. Sect. IA 18 (1971) 379). In the course of the proof, we will make use of a recent innovation of Schmid–Vilonen (Invent. Math. 124 (1996) 451) in the representation theory (in the theory of index theorems for constructible sheaves). r 2003 Elsevier Science (USA). All rights reserved. MSC: 32C38; 35A27 Keywords: D-module; Holonomic system; Index theorem 1. Introduction The aim of this paper is to prove a useful formula to compute the exact dimensions of the solutions to holonomic D-modules. The study of the dimension formula for the generalized function solutions to ordinary differential equations started only recently. In the 1970s, a beautiful theorem was obtained by Kashiwara [7] and Komatsu [12] using the hyperfunction theory.
    [Show full text]
  • Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J
    Writing Mathematical Expressions in Plain Text – Examples and Cautions Copyright © 2009 Sally J. Keely. All Rights Reserved. Mathematical expressions can be typed online in a number of ways including plain text, ASCII codes, HTML tags, or using an equation editor (see Writing Mathematical Notation Online for overview). If the application in which you are working does not have an equation editor built in, then a common option is to write expressions horizontally in plain text. In doing so you have to format the expressions very carefully using appropriately placed parentheses and accurate notation. This document provides examples and important cautions for writing mathematical expressions in plain text. Section 1. How to Write Exponents Just as on a graphing calculator, when writing in plain text the caret key ^ (above the 6 on a qwerty keyboard) means that an exponent follows. For example x2 would be written as x^2. Example 1a. 4xy23 would be written as 4 x^2 y^3 or with the multiplication mark as 4*x^2*y^3. Example 1b. With more than one item in the exponent you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x2n must be written as x^(2n) and NOT as x^2n. Writing x^2n means xn2 . Example 1c. When using the quotient rule of exponents you often have to perform subtraction within an exponent. In such cases you must enclose the entire exponent in parentheses to indicate exactly what is in the power. x5 The middle step of ==xx52− 3 must be written as x^(5-2) and NOT as x^5-2 which means x5 − 2 .
    [Show full text]
  • Assessment of Options for Handling Full Unicode Character Encodings in MARC21 a Study for the Library of Congress
    1 Assessment of Options for Handling Full Unicode Character Encodings in MARC21 A Study for the Library of Congress Part 1: New Scripts Jack Cain Senior Consultant Trylus Computing, Toronto 1 Purpose This assessment intends to study the issues and make recommendations on the possible expansion of the character set repertoire for bibliographic records in MARC21 format. 1.1 “Encoding Scheme” vs. “Repertoire” An encoding scheme contains codes by which characters are represented in computer memory. These codes are organized according to a certain methodology called an encoding scheme. The list of all characters so encoded is referred to as the “repertoire” of characters in the given encoding schemes. For example, ASCII is one encoding scheme, perhaps the one best known to the average non-technical person in North America. “A”, “B”, & “C” are three characters in the repertoire of this encoding scheme. These three characters are assigned encodings 41, 42 & 43 in ASCII (expressed here in hexadecimal). 1.2 MARC8 "MARC8" is the term commonly used to refer both to the encoding scheme and its repertoire as used in MARC records up to 1998. The ‘8’ refers to the fact that, unlike Unicode which is a multi-byte per character code set, the MARC8 encoding scheme is principally made up of multiple one byte tables in which each character is encoded using a single 8 bit byte. (It also includes the EACC set which actually uses fixed length 3 bytes per character.) (For details on MARC8 and its specifications see: http://www.loc.gov/marc/.) MARC8 was introduced around 1968 and was initially limited to essentially Latin script only.
    [Show full text]
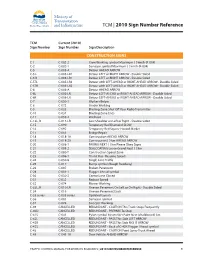
  • 2010 Sign Number Reference for Traffic Control Manual
    TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34
    [Show full text]
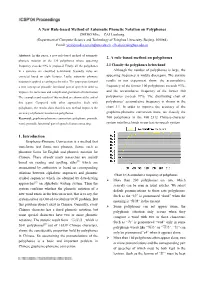
  • A New Rule-Based Method of Automatic Phonetic Notation On
    A New Rule-based Method of Automatic Phonetic Notation on Polyphones ZHENG Min， CAI Lianhong (Department of Computer Science and Technology of Tsinghua University, Beijing, 100084) Email: [email protected], [email protected] Abstract: In this paper, a new rule-based method of automatic 2. A rule-based method on polyphones phonetic notation on the 220 polyphones whose appearing frequency exceeds 99% is proposed. Firstly, all the polyphones 2.1 Classify the polyphones beforehand in a sentence are classified beforehand. Secondly, rules are Although the number of polyphones is large, the extracted based on eight features. Lastly, automatic phonetic appearing frequency is widely discrepant. The statistic notation is applied according to the rules. The paper puts forward results in our experiment show: the accumulative a new concept of prosodic functional part of speech in order to frequency of the former 100 polyphones exceeds 93%, improve the numerous and complicated grammatical information. and the accumulative frequency of the former 180 The examples and results of this method are shown at the end of polyphones exceeds 97%. The distributing chart of this paper. Compared with other approaches dealt with polyphones’ accumulative frequency is shown in the polyphones, the results show that this new method improves the chart 3.1. In order to improve the accuracy of the accuracy of phonetic notation on polyphones. grapheme-phoneme conversion more, we classify the Keyword: grapheme-phoneme conversion; polyphone; prosodic 700 polyphones in the GB_2312 Chinese-character word; prosodic functional part of speech; feature extracting; system into three kinds in our text-to-speech system 1.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]
  • Linear Algebra) 2
    MATH 680 Computation Intensive Statistics December 3, 2018 Matrix Basics Contents 1 Rank (linear algebra) 2 1.1 Proofs that column rank = row rank . .2 1.2 Properties . .4 2 Kernel (linear algebra) 5 2.1 Properties . .6 2.2 Illustration . .9 3 Matrix Norm 12 3.1 Matrix norms induced by vector norms . 12 3.2 Entrywise matrix norms . 14 3.3 Schatten norms . 18 1 1 RANK (LINEAR ALGEBRA) 2 4 Projection 19 4.1 Properties and classification . 20 4.2 Orthogonal projections . 21 1 Rank (linear algebra) In linear algebra, the rank of a matrix A is the dimension of the vector space generated (or spanned) by its columns. This corresponds to the maximal number of linearly independent columns of A. This, in turn, is identical to the dimension of the space spanned by its rows. The column rank of A is the dimension of the column space of A, while the row rank of A is the dimension of the row space of A. A fundamental result in linear algebra is that the column rank and the row rank are always equal. 1.1 Proofs that column rank = row rank Let A be an m × n matrix with entries in the real numbers whose row rank is r. There- fore, the dimension of the row space of A is r. Let x1; x2; : : : ; xr be a basis of the row space of A. We claim that the vectors Ax1; Ax2; : : : ; Axr are linearly independent. To see why, consider a linear homogeneous relation involving these vectors with scalar coefficients c1; c2; : : : ; cr : 0 = c1Ax1 + c2Ax2 + ··· + crAxr = A(c1x1 + c2x2 + ··· + crxr) = Av; 1 RANK (LINEAR ALGEBRA) 3 where v = c1x1 + c2x2 + ··· + crxr: We make two observations: 1.
    [Show full text]